碳酸盐岩储层有电阻率高、声波时差低、密度大的特点，流体对电测井的贡献小，利用电测井进行流体识别具有一定的局限性，为此，可借助于流体与干岩石的声波、密度等弹性信息的差异进行流体识别(司马立强等，2009).利用弹性信息进行流体识别时，通常必须已知储层的岩石物理性质，在缺少岩石物理实验数据的情况下，利用流体替换方法实现流体识别具有重要的研究意义和实际应用价值.流体替换的核心为Gassmann等效介质理论(Gassmann，1951)，基于该理论国内外学者针对碳酸盐岩储层流体替换进行了很多研究(王炳章，2008).Voigt(1928)Reuss(1929)提出了两个不同的矿物的混合平均模型，Hill(1952)给出Voigt上界和Reuss下界的算术平均值.Wood(1955)提出的孔隙流体模量模型常用于估算孔隙流体的有效体积模量.张金强等(2010)提出对某些超致密的碳酸盐岩使用统计平均法求其固体基质弹性参数，计算结果更加准确，但需结合岩性解释和孔隙度解释结论，求取与储层段同一岩性(或近似岩性)、孔隙度小于某个特定值的岩层段的纵横波速度、密度的平均值.林凯等(2009)利用Biot系数求取干岩石的体积模量，利用替换后目的层等效参数，实现了岩性预测，并为气水识别提供了依据(史燕红，2009；林凯，2010).本文在前人基础上，根据实际测井数据，应用反推法计算干岩石体积模量，并对计算结果进行分析筛选，提取合理的干岩石体积模量，使结果更准确可靠，流体替换之后不同流体类型纵波时差数值差异较大，识别流体效果明显.

1 流体替换方法原理 1.1 方法原理

Gassmann方程推导了储层充满流体的弹性模量公式，奠定了沉积岩的弹性特性和物性之间研究的基础(Gassmann，1951).该方程给出了饱和岩石有效体积模量与干岩石体积模量、矿物基质体积模量、孔隙流体体积模量，以及孔隙度之间的关系(Han et al.，2004).已知储层条件(地层温度、地层压力、孔隙度、岩石基质类型和盐水矿化度)和孔隙流体类型，利用Gassmann方程计算碳酸盐岩储层的密度，纵横波速度，如下即为基于测井数据和测试数据实现流体替换的方法与步骤.

1)计算流体密度

已知油、气、水的饱和度和密度，可求得孔隙流体的等效密度为(林凯等，2009)

式中，ρ_fl为孔隙流体的平均密度.ρ_o、ρ_g和ρ_w分别为流体中原油的密度、气的密度、盐水的密度，S_o、S_g和S_w分别表示含油饱和度、含气饱和度和含水饱和度.

2)计算流体的体积模量

利用Wood方程可以计算出混合流体的体积模量为

式中，K_fl为混合流体的体积模量，K_o、K_g和K_w分别为原油的体积模量、气的体积模量、盐水的体积模量，S_o、S_g和S_w分别表示含油饱和度、含气饱和度和含水饱和度.

3)计算饱和岩石弹性模量并应用反推法计算干岩石体积模量

在已知饱和岩石纵横波速度和密度的前提下，利用Gassmann方程来计算干岩石的弹性模量为

式中，ρ_b为测井所得密度资料，Vp、Vs为饱和岩石的纵横波速度，由阵列声波测井纵波时差和横波时差资料计算得到.μ_sat=μ_dry为岩石剪切模量(Gregor et al.，2009)，M_sat为饱和岩石弹性模量.根据公式(3)计算得到的岩石剪切模量和公式(4)计算得到的饱和岩石弹性模量，可得饱和岩石有效体积模量为

式中，K_sat为饱和岩石有效体积模量.为了简化公式，引入a、b分别表示为

式中，K₀和K_fl分别为基质矿物(颗粒)体积模量、流体体积模量，φ为岩石孔隙度，由测井资料计算得到，公式为

式中，K_dry为干岩石(骨架)有效体积模量.

4)计算替换后流体的密度以及体积模量

已知替换流体的饱和度和密度，可得到替换后孔隙流体的密度为

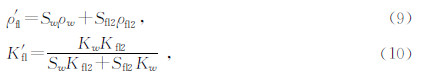
式中，ρ′_fl为流体替换后孔隙流体的密度.ρ_fl2为替换流体的密度，S_fl2为替换流体的饱和度，K′_fl为流体替换后孔隙流体的体积模量.

5)计算进行替换后岩石的密度以及纵波速度

根据公式(9)计算得到替换流体密度ρ′_fl，以及测井计算的孔隙度φ得到流体替换后饱和岩石的密度为

式中，ρ_sat为流体替换后饱和岩石的密度，ρ₀为基质矿物平均密度.Gassmann方程表示为

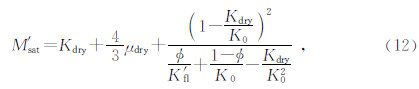
式中，M′_sat为流体替换后饱和岩石的弹性模量.结合公式(9)得到的流体替换后饱和岩石的密度ρ_sat，容易求得流体替换后饱和岩石的纵波速度(Laas et al.，2008)为

式中，V′_p为流体替换后饱和岩石的纵波速度.

首先准备数据，主要包括搜集目的层段盐水、原油和气的密度、速度等物理参数，其次必需的测井数据有：密度测井和阵列声波提供的纵波和横波时差数据.然后，利用测井资料进行岩性识别，并生成岩性曲线，计算储层的孔隙度和含水饱和度；最后，利用上述流体替换方法和流程分别进行了饱含水、饱含油和饱含气的流体替换，计算得到替换后饱和岩石的纵波时差、密度、孔隙度、体积模量以及干岩石体积模量等岩石物理参数.

应用上述流体替换方法，针对塔河地区奥陶系碳酸盐岩储层，基于测井资料和流体性质以及地层压力温度等参数，分别进行了饱含水、饱含油和饱含气的流体替换研究.

A井是来自塔河油田的一口井，对该井用流体替换方法进行了数据处理，如图 1所示.可以看到，在高孔隙度层段，例如储层段5710~5720 m处，流体替换为油(即饱含油)时计算的岩石纵波时差曲线与实际声波测井曲线几乎重合，而流体替换为气和水(即饱含气和水)时计算的纵波时差曲线与声波测井曲线存在明显差异，这说明此层段为油层.然而，不同流体替换实验中计算的密度曲线与实际密度测井曲线几乎重合，这说明流体对密度不敏感.对于该目的层的低孔隙度段，例如图中5733~5734 m段，流体替换后声波时差曲线和密度曲线与实际声波测井曲线和密度测井曲线基本重合，这说明流体对低孔隙的饱和岩石参数的影响不大.

图 1

Fig. 1

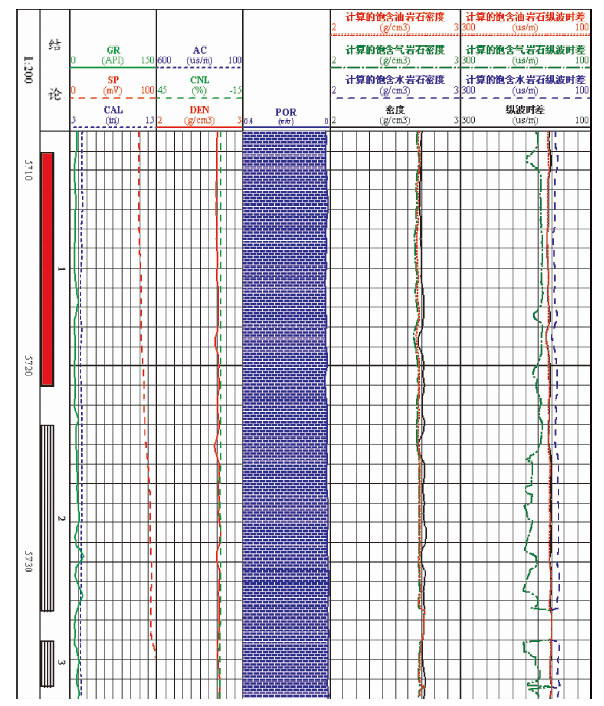图 1A井流体替换方法测井解释结果 Fig. 1 The log interpretation results of well A using fluid substitution method

根据公式e=(ρ－ρ′)/ρ与e=(V_P-V′_P)/V_P计算每一个深度点测井数据与流体替换后数据的相对误差，取该层段相对误差的平均值，计算结果见表 1.孔隙中流体的密度对饱和岩石的密度影响不大，饱含水、油和气的相对误差均较小，且数值接近，不易识别流体类型.而纵波时差参数，孔隙饱含油时与实测数据相对误差最小，并与饱含水、气的相对误差存在较大差异，有利于识别流体.

表 1(Table 1)

表 1 饱和岩石实测与模拟的声波时差和 密度数据相对误差 Table 1 Relative errors between measured and simulated density and compressional acoustic slowness of saturated rock 孔隙流体类型 实测与正演密度 相对误差 实测与正演纵波 时差相对误差 饱含水 0.008562 0.063693 饱含油 0.009375 0.005974 饱含气 0.013383 0.113772

表 1 饱和岩石实测与模拟的声波时差和 密度数据相对误差 Table 1 Relative errors between measured and simulated density and compressional acoustic slowness of saturated rock

对实测数据与正演数据进行交会图分析(如图 2)，可以看到纵波时差参数由于流体性质不同而存在明显差异，有利于识别流体，而密度参数数据很难分辨.从上述相对误差分析和图中的结果对比，可以得出基于密度的流体替换的效果不如基于声波的流体替换好.

图 2

Fig. 2

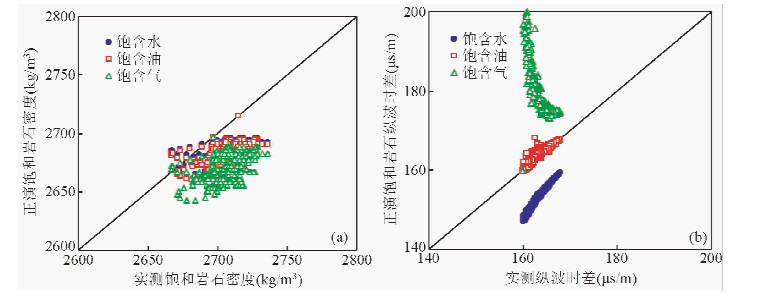图 2A井流体替换实验结果与密度、声波参数对流体敏感性分析 (a) 密度参数; (b) 纵波时差. Fig. 2 Fluid substitution results and sensitivity of density and compressional acoustic slowness to fluids in fluid substitution experiments in well B (a) Density parameter; (b) Compressional slowness.

综上所述判断此层段为油层.该井在5712~5733 m进行测试，试油结果投产初期产液22.0方，其中产油21.6方，水0.6方，试油结果为油层.这验证了利用流体替换方法进行流体识别的结果是正确的.

B井为哈拉哈唐地区的另一口井，用本文方法对测井数据进行了数据处理与解释.图 3为流体替换方法测井解释结果.

图 3

Fig. 3

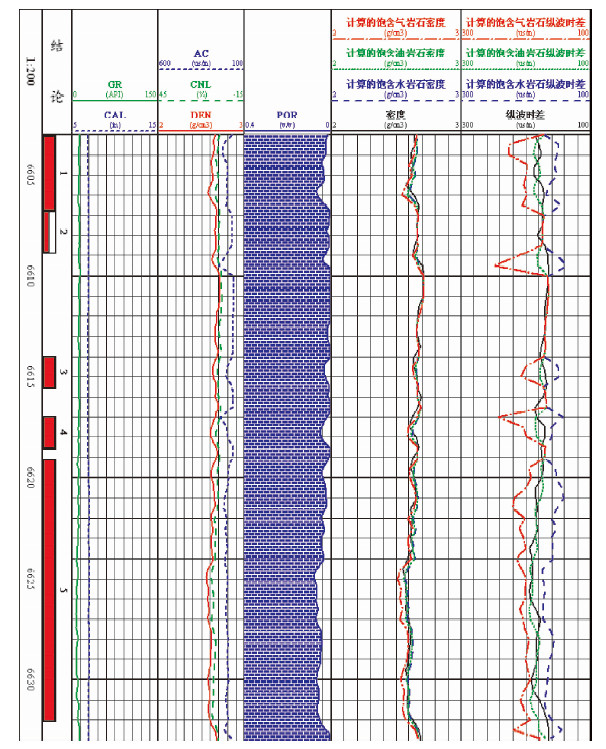图 3B井流体替换方法测井解释结果 Fig. 3 The log interpretation results of well B using fluid substitution method

计算结果表明，该井在目的储层的低孔隙度层段，流体替换后各种流体类型的纵波时差曲线与声波测井曲线几乎吻合，差异不明显；而在高孔隙层段，流体替换后的纵波时差曲线与声波测井曲线存在明显差异，而且饱含油的岩石纵波时差曲线与原位测井曲线几乎重合.根据公式e=(ρ－ρ′)/ρ与e=(V_P-V′_P)/V_P计算每一个深度点测井数据与流体替换后数据的相对误差，取该层段相对误差的平均值，计算结果见表 2.岩石饱含油时与测井数据相对误差最小.

表 2(Table 2)

表 2 B井饱和岩石实测与模拟的声波时差和 密度数据相对误差 Table 2 Relative errors between measured and simulated density and compressional acoustic slowness of saturated rock in well B 孔隙流体类型 实测与正演密度 相对误差 实测与正演纵波 时差相对误差 饱含水 0.00813 0.120554 饱含油 0.007234 0.042142 饱含气 0.010556 0.146849

表 2 B井饱和岩石实测与模拟的声波时差和 密度数据相对误差 Table 2 Relative errors between measured and simulated density and compressional acoustic slowness of saturated rock in well B

对实测饱和岩石密度与流体替换计算结果所得正演饱和岩石密度数据，实测纵波时差与流体替换计算结果所得的正演纵波时差数据进行交会图分析(如图 4).图中发现密度参数数据很难分辨，纵波时差参数由于流体性质不同而存在明显差异，利于识别流体.

图 4

Fig. 4

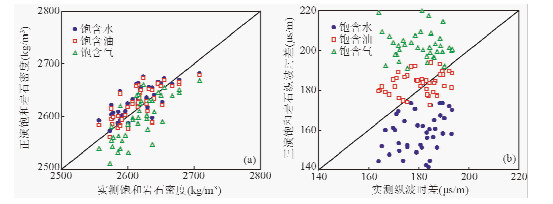图 4 B井流体替换实验结果与密度、声波参数对流体敏感性分析 (a) 密度参数; (b) 纵波时差. Fig. 4 Fluid substitution results and sensitivity of density and compressional acoustic slowness to fluids in fluid substitution experiments in well B (a) Density parameter; (b) Compressional slowness.

综上所述，判断此层段为油层.该井在6613~6635 m进行测试，日产油64.48 t，日产水2.82 t，含水4%，试油结果为油层.解释结果与试油结果一致.

3.1     本次研究针对碳酸盐岩储层流体识别难题，基于声波、密度测井数据和Gassman理论进行了流体替换分析，根据流体替换后计算的密度和声波与原位测井数据的差异性来推断和识别流体性质.

3.2     研究区应用实例表明，该流体替换方法能够用于碳酸盐岩储层的流体识别，基于纵波时差的流体替换识别流体比基于密度的流体替换效果好，说明流体对纵波时差比对密度敏感.在碳酸盐岩储层的高孔隙层段，流体替换后效果较好，而对于低孔隙度层段，其流体贡献小流体替换效果不好，这说明该方法尤其适用于孔隙度较高储层.