微地震正演模拟,目前一般是沿用地震勘探的有限差分方法(王守东,2003)和射线追踪(Leidenfrost et al.,1999;宋维琪等,2003)方法.随着微地震技术的应用的不断扩大,实际生产应用中发现了许多问题(Raab and Coyne,1997).其中最关键的问题是定位精度(宋维琪和杨晓东,2011)和实时监测的问题(Wolhart et al.,2006;De Meersman et al.,2009).
另外,微地震定位结果的最优解释,也是面临急需解决的问题(Pei et al,2009),而这其中涉及微地震震源的反演,为了反演震源,走时反演已远不能满足问题的要求(张晓林等,2013),快速的波场正演,是摆在我们面前的重要任务.考虑井中接收观测方式以及激发和接收边界条件的复杂性,有限差分方法正演结果的精度不能够保证.
鉴于以上分析,研究了微地震波场模拟的快速数值方法,把解微分方程的模式匹配理论(Liu et al.,1990;Fan et al.,2000;Li et al.,2005)引用到本研究中,将以上模型的正演问题,变成纵向采用解析方法横向采用有限元的组合方法.
1 基本方程和边界条件对于井中观测的微地震监测问题,由于观测是沿垂直方向观测的,可以看作是二维问题,满足波动方程(王晨龙等,2013)

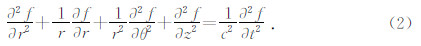
当波场具有轴对称性质时,波函数与方位角无关,波动方程变为
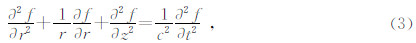
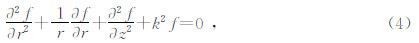
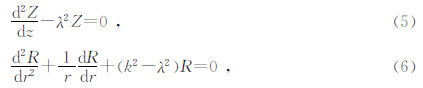
本征函数应满足如下边界条件:
(1)自然边界条件
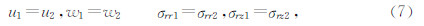
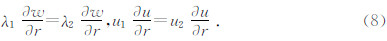
如果设定地层的速度模型为水平层状模型,并且波场在径向变化以源为中心具有轴对称特点(Chew et al,1984).问题求解在垂直方向采用解析方法、径向采用数值方法的混合方法,公式为
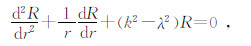


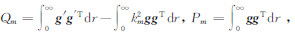
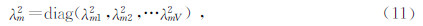
式(10)是一个广义特征值问题,通过求解广义特征值,可以得到各层的本征值和本征向量.考虑位移应力连续条件,方程(5)的解为
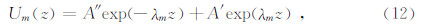

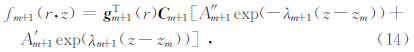
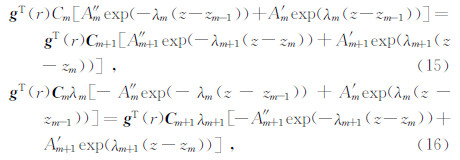
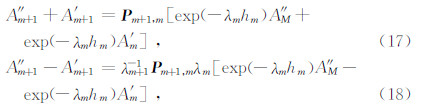
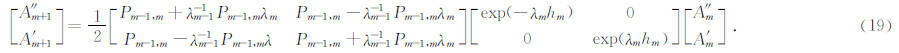
研究问题是轴对称波场,除了速度模型具有轴对称特点外,震源能量辐射也应该满足轴对称的特点.微地震震源一般近似为能量均匀辐射的点震源,满足研究问题条件.对于微地震集中力源,等效垂直力源可以满足轴对称解条件,但对于水平方向的集中力源轴对称则满足条件,否则不满足条件.这里考虑满足轴对称源条件.
本文采用垂直方向的集中力源,即:
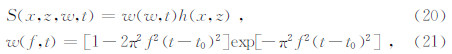
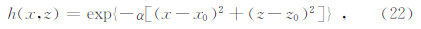
基函数采用有限元方法中讨论的HELMIT内插基函数,具体为

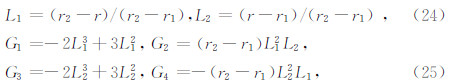
定义于单元内部上述基函数,它满足下列条件:
(1)在节点i处,Gi=1,G′ i=1,在其他节点处,Gi=0,G'i=0,式中Gi为原函数基函数,G′i为原函数导数的基函数.
(2)能保证用它定义的未知量在相邻单元之间的原函数及其一阶导数连续.
(3)应包含任意线性项,使用它定义的单元唯一可满足边界条件.
(4)应满足下列等式:∑Gi=1,∑G′i=1∑=1.
3.2 径向截断边界条件处理在地震波场有限差分数值正演方法中,对边界条件的处理大多采用吸收边界条件.考虑到有限单元的离散和组装特点,径向截断边界条件采无穷单元自然衰减边界条件.具体思路是:在径向有限范围内,离散成一系列的单元,对于截断范围之外,采用一个的较大的单元,根据自然边界条件,r→∞,U→0,保证波场自然衰减.
 | 图 1 单元示意图 Fig. 1 The diagram of elemennt |
对于一个单元e,其两个节点是I,I+1单元的长度为L,采用局部坐标,记
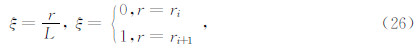
已知节点位移,要求节点间任意一点的位移,利用插值方法来计算,公式为

同样得位移的导数为

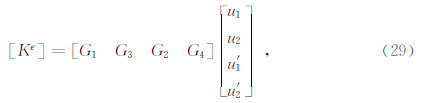
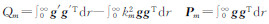 分别建立具体的单元阵,对各单元阵进行组装形成总矩阵,最终形成广义特征方程组,
分别建立具体的单元阵,对各单元阵进行组装形成总矩阵,最终形成广义特征方程组,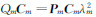 ,解此广义特征方程组便可求出广义特征值和特征向量,把求得的特征值和前面求出的系数A′,A′代入以下方程便可求出一个谐波的位移,再对其进行傅里叶逆变换,最终求得时空域微地震位移数值解,公式为
,解此广义特征方程组便可求出广义特征值和特征向量,把求得的特征值和前面求出的系数A′,A′代入以下方程便可求出一个谐波的位移,再对其进行傅里叶逆变换,最终求得时空域微地震位移数值解,公式为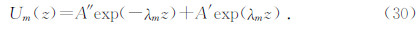
为了验证方法的正确性,设计了水平层状模型且为了与一维射线追踪方法对比,设定横向速度不变.以源为轴对称中心,左右分别划分10个单元,每个单元横向大小为20 m.源放在检波器排列的上方埋深在1950 m处,坐标原点在检波器的位置.两种方法的走时对比结果如表 1所示.从结果看到,两种方法计算的走时是一致的.图 2为模拟的波形结果,图中第一个同相轴为P波,第二个同相轴为S波.随着观测点离开源位置的变化,逐渐出现了较弱的转换波.结果说明正演模拟方法是正确的,模拟结果是可靠的.
|
|
表 1 速度模型和两种方法的走时计算结果 Table 1 The velocity model and calculation result of two method |
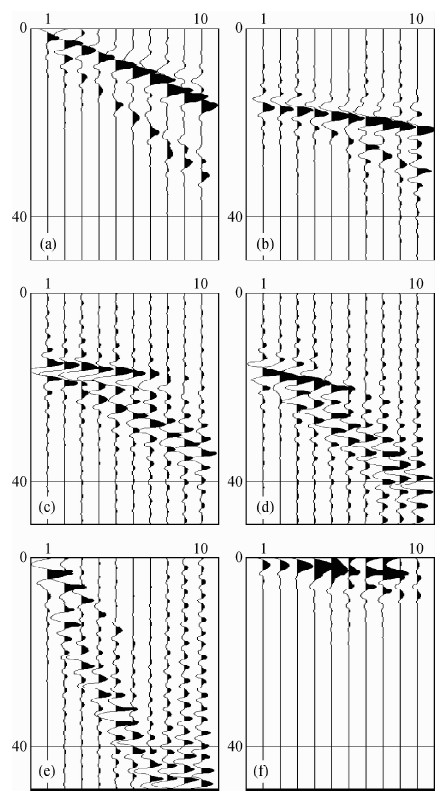 |
图 2 不同源位置的波形记录 (a)R=200 m; (b)R=250 m; (c)R=400 m; (d) R=450 m; (e) R=1000 m; (f) R=10 m. 图中横坐标为检波器道号,纵坐标为采样点数, (a)—(f)为检波器与震源不同距离 Fig. 2 The waveform recording of Different source location The horizontal axis is detector number and vertical axis is sampling number. The figure(a)—(f)are different distance between source and detector. |
分析图 2各个结果图,垂直排列检波器记录微地震波的响应变化,随着离震源的不同距离,其变化特征明显不同,在震源附近,地震波接近垂直入射,没有转换波,PS波比较清楚,PS波的能量变化随着垂直排列检波器,由近到远能量逐渐增大.随着离开源的距离增大,出现转换波,这时P波的转换波和原始的S波干涉,使的地震记录同相轴零乱. 当距离很远时,只能看到S波和其转换波.当距离很近时,只有PS波.在源的上方P波顶能量较强,随着离开源的距离增大,能量逐渐衰减.在P波以后的区域波场相对复杂,在源的上方S波较单一,S波的极性为反极性.随着离开源距离的增大,S波和P波的转换波干涉,使的波形发生畸变,随着距离的依次增大,S波和转换的S波能量逐渐增大,之后又逐渐衰减,随着距离的再次增大,S波同相轴向上移动,出现折射S波.
5 结 论5.1 对于微地震波动方程,在轴对称速度模型和震源均匀辐射情况下,在高频条件下,可以利用分离变量法把波动方程进行分解为垂直方向和径向方向两个方程.为了求得方程的解,利用模式匹配理论,把解微分方程的模式匹配理论引用到本研究中,研究形成了水平轴对称层状模型下,纵向采用解析方法横向采用有限元的混合方法.把计算范围截断边界条件,采取无穷大单元自然衰减边界条件的办法,使计算边界的响应变得较小.通过理论和实际论证和验证了研究方法的正确合理性,并和基于射线追踪的走时反演结果进行了对比分析,证明结果精度满足实际要求.
5.2 微地震波场的响应与空间距离关系是非线性的,本文在算法研究时,采用单元两节点线性插值计算,为了进一步提高结果的精度,建议再进行研究时,采用单元三节点二次插值方法.
致 谢 感谢审稿专家和编辑部的大力支持.| [1] | Chew W C, Barone S, Anderson B, et al. 1984. Diffraction of axisymmetric waves in a borehole by bed boundary discontinuities[J]. Geophysics, 49(10):1586-1595. |
| [2] | De Meersman K, Kendall J M, van der Baan M. 2009. The 1998 Valhall microseismic data set:An integrated study of relocated sources,seismic multiplets,and S-wave splitting[J]. Geophysics, 74(6):B183-B195. |
| [3] | Fan G X, Liu Q H, Blanchard S P. 2000. 3-D numerical mode-matching (NMM) method for resistivity well-logging tools[J]. IEEE Transactions on Antennas and Propagation, 48(10):1544-1552. |
| [4] | Leidenfrost A, Ettrich N, Gajewski D, et al. 1999. Comparison of six different methods for calculating traveltimes[J] Geophysical Prospecting, 47(3):269-297. |
| [5] | Li A Y, Nie Z P, Zhao Y W. 2005. Numerical mode matching method with perfectly matching layer[C].//Proceedings of 2005 IEEE Antennas and Propagation Society International Symposium. Washington, DC:IEEE, 4B:372-375. |
| [6] | Liu Q H, Chew W C. 1990. Numerical mode-matching method for the multiregion vertically stratified media[EM wave propagation] [J]. IEEE Transactions on Antennas and Propagation, 38(4):498-506. |
| [7] | Pei D H, Quirein J A, Cornish B E, et al. 2009. Velocity calibration for microseismic monitoring:A very fast simulated annealing (VFSA) approach for joint-objective optimization[J]. Geophysics, 74(6):WCB47-WCB55. |
| [8] | Raab F, Coyne D. 1997. Effect of Micro-seismic noise on a LIGO interferometer[R]. LIGO-T960187-02. California Institute of Technology. |
| [9] | Song W Q, Gao Y K, Zhu H W. 2013. The differential evolution inversion method based on Bayesian theory for micro-seismic data[J]. Chinese Journal of Geophysics (in Chinese), 56(4):1331-1339, doi:10.6038/cjg20130427. |
| [10] | Song W Q, Yang X D. 2011. Micro-seismic events recognition and inversion in the case of single seismic phase[J]. Chinese Journal of Geophysics (in Chinese), 54(6):1592-1599, doi:10.3969/j.issn.0001-5733.2011.06.019 |
| [11] | Song W Q, Yang X D. 2012. The multi-wave field forward simulation of micro-seismic based on ray tracing[J]. Progress in Geophysics (in Chinese), 27(4):1501-1508, doi:10.6038/j.issn.1004-2903.2012.04.025. |
| [12] | Tsang L, Chan A K, Gianzero S. 1984. Solution of the fundamental problem in resistivity logging with a hybrid method[J]. Geophysics, 49(10):1596-1604. |
| [13] | Wang C L, Cheng J B, Yin C, et al. 2013. Microseismic events location of surface and borehole observation with reverse-time focusing using interferometry technique[J]. Chinese Journal of Geophysics (in Chinese), 56(9):3184-3196, doi:10.6038/cjg20130931. |
| [14] | Wang S D. 2003. Absorbing boundary condition for acoustic wave equation by perfectly matched layer[J]. Oil Geophysical Prospecting (in Chinese), 38(1):31-34. |
| [15] | Wolhart S L, Odegard C E, Warpinski N R, et al. 2006. Microseismic fracture mapping optimizes development of low-permeability sands of the Williams fork formation in the Piceance Basin[C].//SPE Annual Technical Conference and Exhibition. Expanded Abstracts, 10:9-12S. |
| [16] | Zhang X L, Zhang F, Li X Y, et al. 2013. The influence of Hydraulic fracturing on velocity and microseismic location[J]. Chinese Journal of Geophysics (in Chinese), 56(10):3552-3560, doi:10.6038/cjg20131030. |
| [17] | 宋维琪,高艳珂,朱海伟. 2013.微地震资料贝叶斯理论差分进化反演方法[J].地球物理学报, 56(4):1331-1339, doi:10.6038/cjg20130427. |
| [18] | 宋维琪,杨晓东. 2011.单震相微地震事件识别与反演[J].地球物理学报, 54(6):1592-1599, doi:10.3969/j.issn.0001-5733.2011.06.019. |
| [19] | 宋维琪,杨晓东. 2012.基于射线追踪的微地震多波场正演模拟[J].地球物理学进展, 27(4):1501-1508, doi:10.6038/j.issn.1004-2903.2012.04.025. |
| [20] | 王晨龙,程玖兵,尹陈,等. 2013.地面与井中观测条件下的微地震干涉逆时定位算法[J].地球物理学报, 56(9):3184-3196, doi:10.6038/cjg20130931. |
| [21] | 王守东. 2003.声波方程完全匹配层吸收边界[J].石油地球物理勘探, 38(1):31-34. |
| [22] | 张晓林,张峰,李向阳,等. 2013.水力压裂对速度场及微地震定位的影响.地球物理学报, 56(10):3552-3560, doi:10.6038/cjg20131030. |
 2015, Vol. 30
2015, Vol. 30

