2. 中南大学地球科学与信息物理学院, 长沙 410083
2. Central south university school of geosciences and info-physics, ChangSha 410083, China
大地电磁测深法(MT)是研究地球深部电性结构的一种地球物理方法(陈乐寿,2009).通过在野外进行五分量(Ex、Ey、Hx、Hy、Hz)观测后,计算得到的倾子资料,对存在横向电性不均匀地质体的分界面(胡文宝等,1997;余年等,2007)具有较好的反映,在实测资料的定性解释(林昌洪等,2011;柳建新等,2012)中起到举足轻重的作用.因此,从理论上分析研究倾子资料的特征和规律也显得十分必要.
在大地电测深法中,假设场源是垂直入射的平面波,即一次场中不存在垂直分量,在横向均匀的一维介质条件下,二次场中也不会产生出垂直磁场,只有在横向不均匀的二维介质和三维介质时才会出现垂直磁场分量(陈乐寿和王光锷,1990).当地下介质的电阻率分布横向不均匀,即具有水平非均匀特性时,在地表观测到的垂直磁场分量Hz≠0,这时,垂直磁场分量Hz与两个水平磁场分量Hx和Hy之间存在的复系数线性关系为

倾子矢量的两个分量Tzx和Tzy,可以直接从观测资料通过最小二乘法求得.一般来说,由于倾子矢量是复数,故存在实部、虚部、振幅和相位四个分量,通过对不同分量的分析研究,可以了解到地下介质横向电性分界面的情况.
1 倾子正演理论在地下介质表现出横向不均匀的二维性质时,由麦克斯韦电磁理论方程组可以推导出TE极化模式下的电磁波满足如下关系:

将(2)式中方程组的前两式带入第三式可以得出
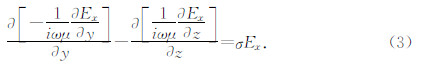
对于地下介质中的σ和μ均匀分布的区域,(3)式可简化为

该式即为亥姆霍兹方程.其中k2=iωμσ.通过数值计算方法求解(4)式,通过正演模拟计算,便可以得到电磁场中电场分量Ex的值.同理,利用麦克斯韦方程组通过正演模拟得到电磁场中磁场分量Hz和Hy的值,再根据(1)式,便可以计算出各种理论地电模型下的倾子资料,包括倾子的实部、虚部、振幅和相位.
在二维介质中,当x轴方向与构造走向一致时,y轴方向和z轴方向地下介质电性结构有变化,而x轴方向地下介质电性结构无变化.此时,Hy和Hz不为零,而Hx=0,(1)式变为

为研究倾子资料在二维介质中的特征和变化规律,作者通过设计不同情况下的理论模型,利用PW2D正演程序计算得到了倾子数据.通过对比分析研究,总结出了倾子资料的特性及在不同情况下的变化规律.
首先,构建了如图 1所示的地电模型,在模型中仅存在一个电性分界面.其中,模型左侧地电介质的电阻率为ρ1,右侧介质的电阻率为ρ2.模拟的剖面长度为8000 m.电性分界面位于剖面的正中央位置.模拟的点距为500 m.采用了100~0.01 Hz之间等对数间隔的21个频点.
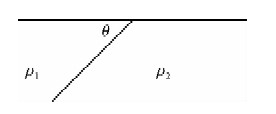 | 图 1 地电模型Ⅰ Fig. 1 Geoelectric model Ⅰ |
设置如图 1所示的地电模型Ⅰ左侧介质的电阻率ρ1与右侧介质的电阻率ρ2之间不同的比值,来研究倾子资料的变化特征,分析总结其规律.为此,固定θ=90°,ρ2=0.1 Ω·m不变,ρ1:ρ2分别取为10:0.1,100:0.1,1000:0.1,10000:0.1四种情况,通过正演模拟计算,得到了如图 2所示的不同比值下频率等于100 Hz时的剖面曲线.
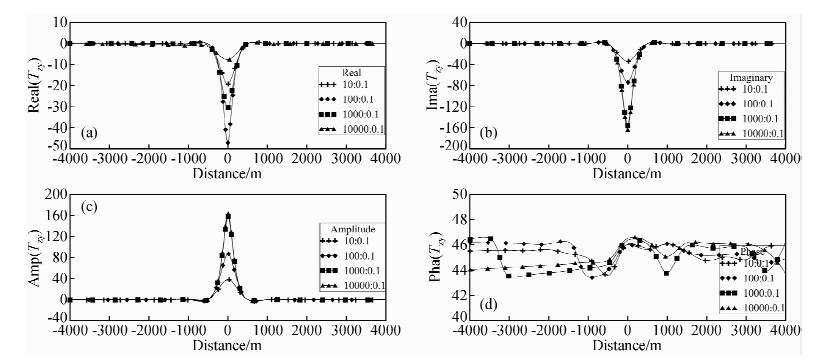 |
图 2 不同比值下垂直界面剖面曲线图 (a)不同电阻率比值下地电模型Ⅰ在频率f=100 Hz时的倾子实部剖面曲线图;(b)不同电阻率比值下地电模型Ⅰ在频率f=100 Hz时的倾子虚部剖面曲线图;(c)不同电阻率比值下地电模型Ⅰ在频率f=100 Hz时的倾子振幅剖面曲线图;(d)不同电阻率比值下地电模型Ⅰ在频率f=100 Hz时的倾子相位剖面曲线图. Fig. 2 Profile graph of vertical interface under different ratios |
通过对比分析研究图 2中倾子资料的剖面曲线变化规律,不难得出,在上述四种情况下,资料的实部、虚部、振幅和相位都能反映出该电性分界面的存在.但各分量在不同比值下,变化规律和异常幅值等特征又不尽相同.随着左侧电阻率的增大,即比值的增大,倾子实部并未随着比值的增大而增大,在ρ1:ρ2=10000:0.1时反而减小.倾子的虚部和振幅的幅值随着比值的增大而增大,但增大的幅度在逐渐减小.倾子的相位随着比值的增大却没有明显的变化,且其幅值变化较小.
2.2 同比值不同电阻率下的倾子资料分析研究固定图 1中地电模型Ⅰ左侧介质的电阻率ρ1与右侧介质的电阻率ρ2的比值为10:1,θ=90°,通过改变两侧地电介质的电阻率值,来研究倾子资料的变化情况.为此,ρ1-ρ2分别设置为10 Ω·m-1 Ω·m,100 Ω·m-10 Ω·m和1000 Ω·m-100 Ω·m三组电阻率值来进行正演模拟计算.得到了频率f=100 Hz时的结果,如下图所示.
图 3所示为频率f=100 Hz,ρ1:ρ2=10:1时,垂直界面下的剖面曲线图.从中不难看出,ρ1-ρ2为10 Ω·m-1 Ω·m时,倾子的实部、虚部和振幅形成一个“陡而窄”的峰值异常,当ρ1-ρ2为1000 Ω·m-100 Ω·m时,异常幅值明显减弱,但其异常范围增大.即在电性分界面左右两侧电阻率比值相同的情况下,随着电性分界面两侧的电阻率值不断升高,倾子资料的实部、虚部和振幅异常的幅值在不断减小,但其异常影响范围却不断扩大.而相位曲线则随着电阻率的不断升高,电性分界面处的异常没有明显的变化.
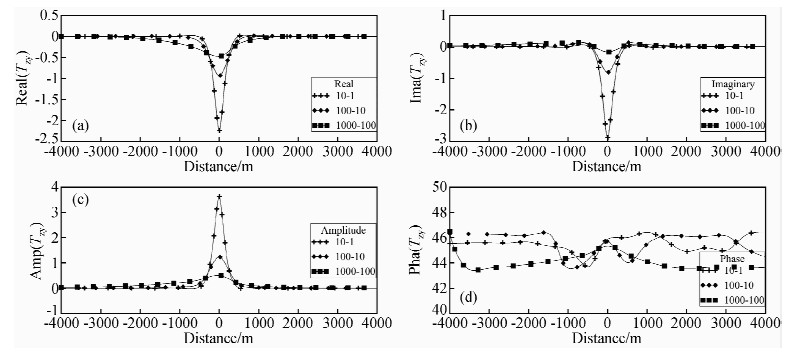 |
图 3 同比值不同电阻率下垂直界面剖面曲线图 (a)同比值不同电阻率下地电模型Ⅰ在频率f=100 Hz时的倾子实部剖面曲线图;(b)同比值不同电阻率下地电模型Ⅰ在频率f=100 Hz时的倾子虚部剖面曲线图;(c)同比值不同电阻率下地电模型Ⅰ在频率f=100 Hz时的倾子振幅剖面曲线图;(d)同比值不同电阻率下地电模型Ⅰ在频率f=100 Hz时的倾子相位剖面曲线图. Fig. 3 Profile graph of vertical interface under the same ratios and different different resistivity |
为研究浅层介质对一定深度下电性分界面倾子资料的影响,在其顶部添加了一定厚度的覆盖层.在此,固定ρ1、ρ2分别为100 Ω·m和10 Ω·m,θ=90°,覆盖层的电阻率为亦为10 Ω·m,取覆盖层厚度分别为0 m,100 m,500 m,1000 m,通过正演计算,得到了倾子资料各分量的变化曲线.根据趋肤深度公式可知,在覆盖层厚度为1000 m时,频率约为2.5 Hz的电磁波可传播到电性分界面顶部.为此,选取了频率f=2.5 Hz时倾子资料的剖面曲线,结果如图 4所示.
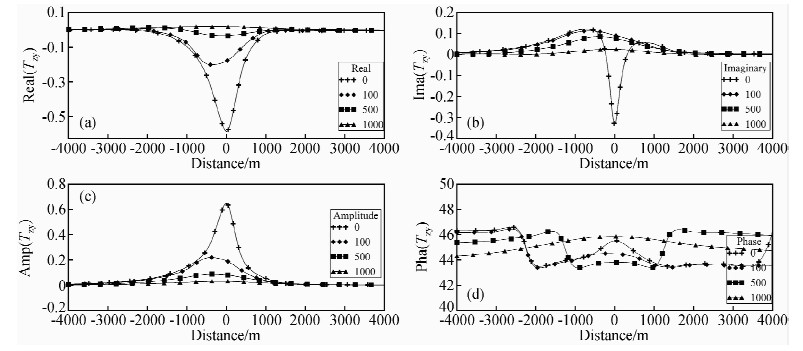 |
图 4 不同厚度覆盖层下垂直界面剖面曲线图 (a)不同厚度覆盖层下地电模型Ⅰ在频率f=2.5 Hz时的倾子实部剖面曲线图;(b)不同厚度覆盖层下地电模型Ⅰ在频率f=2.5 Hz时的倾子虚部剖面曲线图;(c)不同厚度覆盖层下地电模型Ⅰ在频率f=2.5 Hz时的倾子振幅剖面曲线图;(d)不同厚度覆盖层下地电模型Ⅰ在频率f=2.5 Hz时的倾子相位剖面曲线图. Fig. 4 Profile graph of vertical interface under the different thickness of overlay |
从模拟结果中不难看出,在覆盖层分别为0 m,100 m,500 m,1000 m四种情况下,随着覆盖层厚度的增加,倾子资料的实部、虚部和振幅都逐渐减小,但衰减速度又不尽相同,其中虚部异常衰减的速度最快,实部和振幅次之.而相位曲线在四种情况下形态变化幅度较小.在覆盖层厚度为1000 m时,倾子的实部、虚部、振幅和相位异常幅值基本都衰减到零,剖面曲线变成一条直线.
2.4 不同倾角下的倾子资料分析研究前面的对比分析研究,都是基于垂向电性分界面情况下倾子资料的变化规律,即θ=90°.然而实际情况中,地下介质中许多电性分界面并非与地面垂直,而是成一定的夹角.这就需要我们了解在不同倾角下,倾子资料的变化情况.为此,固定ρ1-ρ2=100-10 Ω·m,θ角分别取为30°、45°、90°、135°和150°五种情况进行正演模拟计算,取频率f=10 Hz时的剖面曲线图,结果如图 5所示.
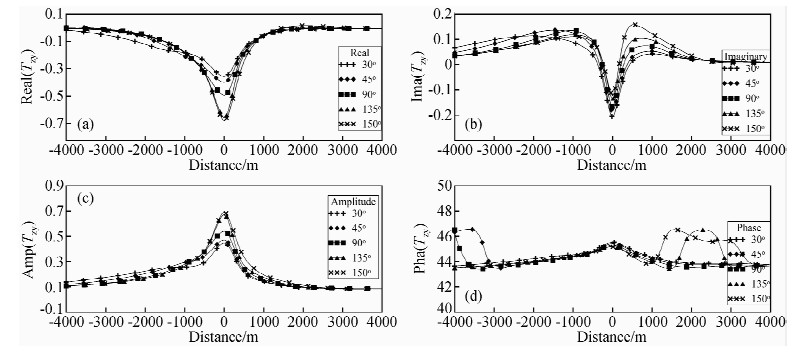 |
图 5 不同倾角接触界面下的倾子剖面曲线图 (a)不同倾角下地电模型Ⅰ在频率f=10 Hz时的倾子实部剖面曲线图;(b)不同倾角下地电模型Ⅰ在频率f=10 Hz时的倾子虚部剖面曲线图;(c)不同倾角下地电模型Ⅰ在频率f=10 Hz时的倾子振幅剖面曲线图;(d)不同倾角下地电模型Ⅰ在频率f=10 Hz时的倾子相位剖面曲线图. Fig. 5 Tipper profile graph of contact interface under different angle |
通过对比分析研究,不难看出,倾角θ在30°、45°、90°、135°和150°五种情况下,倾子资料的实部、虚部、振幅和相位剖面曲线均能反映出电性分界面的存在,但其异常形态并没有随着倾角的变化而发生较明显的变化,并不能很好地反映出电性分界面的倾斜角度.但根据电性分界面两侧的电阻率值高低和曲线的形态,仍可确定出电性分界面的大致倾斜方向.
通过上述研究结果表明,倾子资料对地下介质存在单个横向电性分界面的地质体具有较好的异常反映.但实际地下介质中,往往存在多个横向电性分界面,为研究倾子资料对多个电性分界面的异常反映情况,构建了如图 6所示的二维地电模型.
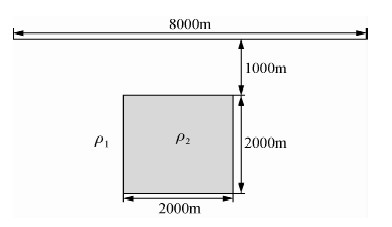 | 图 6 地电模型Ⅱ Fig. 6 Geoelectric model Ⅱ |
模型中围岩的电阻率为ρ1,异常体的电阻率为ρ2,异常体距离地表的高度为1000 m,异常体的规模为2000 m ×2000 m.模拟的剖面长度为8000 m.异常体位于剖面的正中央.模拟的点距为500 m.采用了100~0.01 Hz之间等对数间隔的21个频点.
2.5 低阻异常体下的倾子资料分析研究在地电模型Ⅱ中,取围岩的电阻率为100 Ω·m,异常体的电阻率为10 Ω·m.通过正演计算,绘制了如图 7所示的倾子平面等值线图.
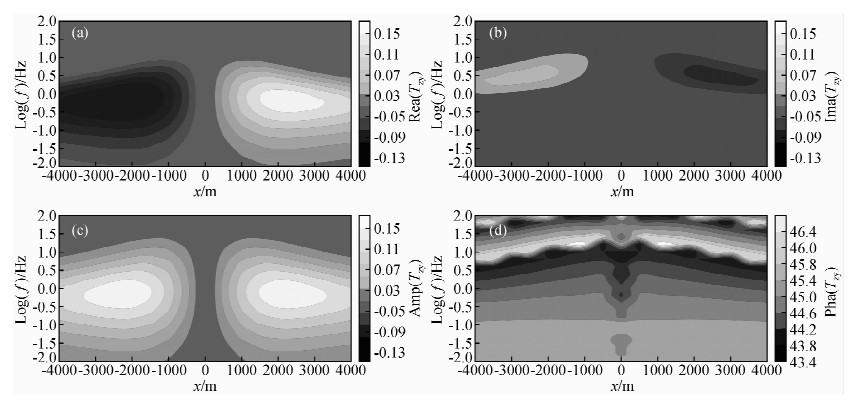 |
图 7 低阻异常体下倾子响应等值线图 (a)地电模型Ⅱ为低阻异常体条件下倾子实部平面等值线图;(b)地电模型Ⅱ为低阻异常体条件下倾子虚部平面等值线图;(c)地电模型Ⅱ为低阻异常体条件下倾子振幅平面等值线图;(d)地电模型Ⅱ为低阻异常体条件下倾子相位平面等值线图. Fig. 7 Tipper contour map of low-resistivity anomaly |
从图 7中可以看出,倾子资料的实部、虚部、振幅和相位对横向不均匀体左右电性分界面均有异常反映,但各分量对异常的反应能力有所差异.其中,倾子资料的实部、虚部和振幅反映较明显,而相位资料反映效果较差,其异常幅度较小,且在浅部出现了虚假异常信息.实部在由高阻到低阻的横向电性分界面处,表现为负异常,在由低阻到高阻的横向电性分界面处,表现为正异常.虚部的正负异常信息则与实部相反.振幅都表现为正异常信息.再根据趋肤深度公 式计算可知,在频率约为25 Hz(Lg(f)=1.4 Hz)时,电磁波传播到低阻异常体顶部.由此可见,倾子资料实部异常信息并未能反映出异常体的顶部位置,而虚部异常能较实部更好地反映出异常体的顶部位置.振幅与实部和虚部相比较,能更好地反映出异常体的顶部和底部位置.再者,不难看出,模型中左右电性分界面均处于异常变化梯度最大的位置.
2.6 高阻异常体下的倾子资料分析研究在地电模型Ⅱ中,取围岩的电阻率为10 Ω·m,异常体的电阻率为100 Ω·m.通过正演模拟计算,得到了如图 8所示的倾子响应等值线图.
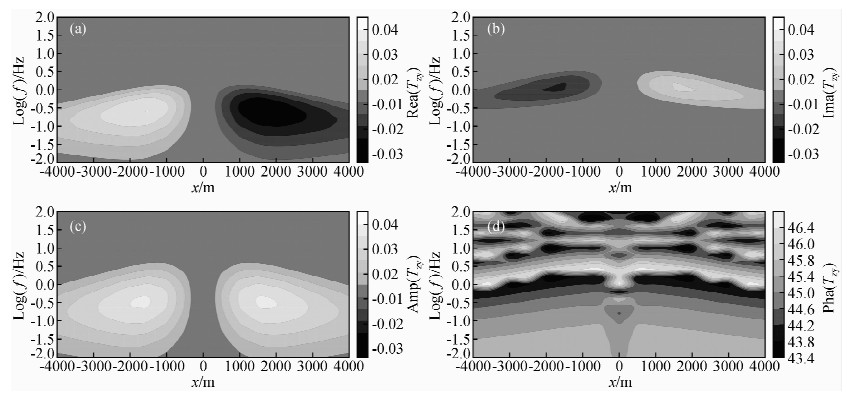 |
图 8 高阻异常体下倾子响应等值线图 (a)地电模型Ⅱ为高阻异常体条件下倾子实部平面等值线图;(b)地电模型Ⅱ为高阻异常体条件下倾子虚部平面等值线图;(c)地电模型Ⅱ为高阻异常体条件下倾子振幅平面等值线图;(d)地电模型Ⅱ为高阻异常体条件下倾子相位平面等值线图. Fig. 8 Tipper contour map of high-resistivity anomaly |
从图 8中可以看出,倾子的实部、虚部、振幅和相位对高阻体左右电性分界面也有所反映.其中,倾子资料的实部、虚部和振幅反映较明显,而相位资料反映效果较差,其异常幅度较小,且在浅部出现了虚假异常信息,从中很难分辨出异常体的有用信息.实部在由低阻到高阻的横向电性分界面处,表现为正异常,在由高阻到低阻的横向电性分界面处,表现为负异常.虚部的正负异常信息则与实部相反.振幅均表现为正异常信息.再根据趋肤深度公式计算可知,在频率约为2.5 Hz(Lg(f)=0.4 Hz)时,电磁波传播到高阻异常体顶部.倾子资料实部反映出的异常信息位置与异常体的实际顶部位置相比较低,而虚部异常较实部能更好地反映出异常体的顶部位置.振幅与实部和虚部相比较,能更好地反映出异常体的顶部和底部位置.且左右电性分界面均处于异常变化梯度最大的位置.
2.7 低阻、高阻异常体下的倾子资料对比分析研究图 9为地电模型Ⅱ分别为低阻异常体和高阻异常体时,在频率为2.5 Hz(lg(f)=0.4 Hz)的情况下,倾子资料的剖面曲线图.通过对比分析研究平面等值线图和剖面曲线图,不难看出倾子资料在低阻和高阻异常体下,具有以下特征,主要表现在:首先,倾子资料的实部、虚部和振幅分量在高低阻中的正负异常变化信息一致,实部由低阻到高阻的横向电性分界面处均表现为正异常,在由高阻到低阻的横向电性分界面处均表现为负异常.虚部由低阻到高阻的横向电性分界面处均表现为负异常,在由高阻到低阻的横向电性分界面处均表现为正异常.振幅则都表现为正异常信息.其次,倾子资料实部反映出的顶部异常信息位置与异常体的实际顶部位置相 比较低,而虚部异常较实部能更好地反映出异常体的顶部位置.振幅与实部和虚部相比较,能更好地反映出异常体的顶部和底部位置.再次,异常体左右电性分界面的位置均处于异常变化梯度最大的位置.最后,异常的幅值和影响范围不同.与低阻体异常响应相比,高阻体的异常幅值要小的多.同时,高阻体异常的影响范围也明显小于低阻体异常影响范围.
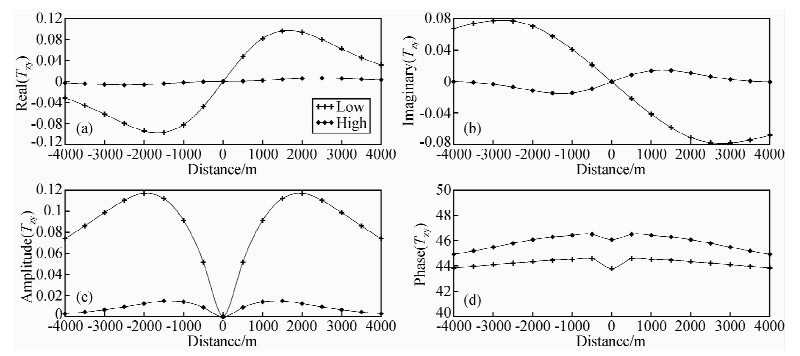 |
图 9 低高阻异常体下倾子响应剖面曲线对比图 (a)地电模型Ⅱ分别为低阻和高阻异常体下在频率f=2.5 Hz时的倾子实部剖面曲线图;(b)地电模型Ⅱ分别为低阻和高阻异常体下在频率f=2.5 Hz时的倾子虚部剖面曲线图;(c)地电模型Ⅱ分别为低阻和高阻异常体下在频率f=2.5 Hz时的倾子振幅剖面曲线图;(d)地电模型Ⅱ分别为低阻和高阻异常体下在频率f=2.5 Hz时的倾子相位剖面曲线图. Fig. 9 Tipper comparison graph of low-resistivity and high-resistivity anomaly |
本文的实际数据来源于国家“深部探测技术预实验研究”专项课题《长江中下游成矿带东部廊带大地电磁探测与技术研究》.研究剖面北起安徽省淮南市地区,进入华北板块(合肥盆地),南达江苏省溧阳市一带,到达扬子古陆内部,整条剖面长达约300 km.跨越了合肥盆地、郯庐断裂、张八岭隆起带、全椒盆地、滁河断裂、长江断裂、含山盆地、马鞍山矿集区、溧水盆地等多个大的地质构造单元.从区域上来说,剖面位于长江中下游成矿带,横跨该成矿带东部关键地段——宁芜矿集区.该剖面的野外工作都采集的数据都是五分量数据.即包含求取倾子资料的垂直磁场分量数据Hz.图 10给出了倾子振幅的拟断面图.从图中可以看出,剖面的左端——合肥盆地,在高频部分,由于地下介质电性结构比较简单,属于沉积地层,倾子资料的振幅几乎为零,这也说明该地区的构造维数为一维.但在中深部,地下结构较之浅部变得复杂,二维偏离度不再为零,倾子振幅也不再为零.在盆地的最右端,与张八岭隆起带相邻,连接处即郯庐断裂的位置,由于有断裂存在,横向电性结构发生了变化,倾子振幅由几乎为零上升到0.5左右.且从浅部到深部,倾子振幅都存在明显的分界面,这也证明郯庐断裂是一深大断裂.在81号和83号测点之间的高频处,也存在有明显的倾子振幅幅值变化,这意味着该处也可能存在断裂.此处,也正是张八岭隆起带与全椒盆地两个地质构造单元的交界面.从野外数据采集过程中得知,65号测点与63号测点分别位于长江两侧,从倾子振幅断面图中也可以看出,在65、63号测点之间,也有一明显的幅值变化,这也证明了长江断裂的存在.在宁芜矿集区内,倾子振幅值都比较大,这说明地下横向电性结构比较复杂,为三维构造. 在47号测深点处,高频部分倾子振幅也存在明显的变化,结合地质分析,该位置可能就是茅山断裂的位置.在剖面的右端宁芜矿集区与溧阳盆地的交界处,倾子振幅也存在着明显变化.
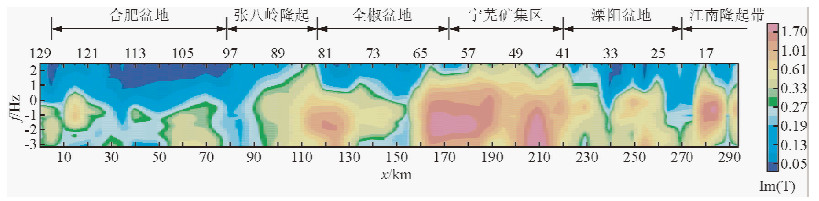 | 图 10 淮南—溧阳剖面倾子振幅断面图 Fig. 10 Tipper amplitude profile of Huainan-Liyang section |
通过上述实例不难看出,倾子资料在大地电磁测深法数据的定性解释中发挥了一定的作用,对存在横向电性不均匀地质体的边界划分或地质构造单位之间边界的划分具有较好的效果.至于如何将其应用到大地电磁测深法数据的定量解释中还需要进一步研究.
4 结 论通过对二维介质中倾子资料的正演模拟计算,并对其异常特征进行对比分析研究,从中不难得出以下结论:
(1)对地下存在横向电性不均匀的地质分界面或地质体,倾子资料的实部、虚部、振幅和相位,在其横向分界面处均有一定程度的异常反映.且横向分界面均处于倾子资料实部、虚部和振幅分量梯度变化值最大的位置.
(2)倾子的相位资料,相对于实部、虚部和振幅来说,异常幅值较小,形态较复杂,其特征不直观,且在浅部会出现虚假异常信息,难以识别.建议在定性分析解释中尽量避免使用倾子相位资料.
(3)当电性分界面左右两侧的电阻率值随着差异的增大,倾子的实部、虚部和振幅异常都有所减小,但虚部衰减的速率最快.
(4)覆盖层的厚度对倾子响应也有一定影响.随着覆盖层厚度的增加,倾子异常幅值不断减小.但各分量的衰减速度不尽相同.其中,虚部衰减速度最快,实部和振幅次之.
(5)倾子响应对电性分界面的倾斜角度反映能力较差.但根据电性分界面两侧电阻率分布情况,在一定程度上,能判断出倾子电性分界面的倾斜方向.
(6)倾子资料实部由低阻到高阻的横向电性分界面处均表现为正异常,由高阻到低阻的横向电性分界面处均表现为负异常.虚部由低阻到高阻的横向电性分界面处均表现为负异常,在由高阻到低阻的横向电性分界面处均表现为正异常.振幅则都表现为正异常信息.
(7)倾子资料的振幅相较于实部和虚部,能更好地反映出异常体顶部和底部的位置信息.
(8)倾子资料对低阻体的反应能力要优于对高阻体的反应能力,其异常幅值要比高阻体大得多.但同时,其异常范围也明显扩大.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [1] | An Zhi-guo, Di Qing-yun. 2006. Discussion on CSAMT resolving power on the thin layer of low resistivity[J]. Seismological and Geomagnetic Observation and Research (in Chinese), 27(2):32-38. |
| [2] | Chen Le-shou. 2009. Magnetotelluric sounding:an effective approach to survey electrical property and state of matter in the deep earth[J]. Chinese Journal of Nature (in Chinese), 31(1):39-46. |
| [3] | Chen Le-shou, Wang Guang-e. 1990. Magnetotelluric Sounding Method (in Chinese)[M]. Beijing:Geological Publishing House. |
| [4] | Chen Qing-li, Hu Wen-bao, Li Jin-ming, et al. 2007. Characteristics of tipper response of buried sphere[J]. Journal of Oil and Gas Technology (J.JPI) (in Chinese), 29(3):75-78. |
| [5] | Chen Xiao-bin, Zhao Guo-ze, Zhan Yan, et al. 2004. Analysis of tipper visual vectors and its application[J]. Earth Science Frontiers (in Chinese), 11(4):626-636. |
| [6] | Han Kai, Liu Guo-xing, Han Jiang-tao, et al. 2012. The deep electrical structure of the Lechang-Xiage profile with MT method[J]. Progress in Geophys. (in Chinese), 27(3):997-1007, doi:10.6038/j.issn.1004-2903.2012.03.021. |
| [7] | Hu Wen-bao, Su Zhu-liu, Chen Qing-li, et al. 1997. Character of tipper data and the application[J]. Oil Geophysical Prospecting (in Chinese), 32(2):202-213. |
| [8] | Jin Sheng, Wei Wen-bo, Ye Gao-feng, et al. 2009. The electrical structure of Bangong-Nujiang suture:results from magnetotelluric sounding detection[J]. Chinese J. Geophys. (in Chinese), 52(10):2666-2675, doi:10.3969/j.issn.0001-5733.2009.10.027. |
| [9] | Jin Wen-guang, Kong Xiang-ru. 2006. Magnetotelluric Impedance Tensor Distortion and Decomposition (in Chinese)[M]. Beijing:Seismological Press. |
| [10] | Labson V F, Becker A. 1987. Natural-field and very low-frequency tipper profile interpretation of contacts[J]. Geophysics, 52(12):1697-1707. |
| [11] | Lin Chang-hong, Tan Han-dong, Tong Tuo. 2011. Three-dimensional conjugate gradient inversion of tipper data[J]. Chinese J. Geophys. (in Chinese), 54(4):1106-1113, doi:10.3969/j.issn.0001-5733.2011.04.026. |
| [12] | Liu Guo-xing, Zhang Xing-zhou, Yang Bao-jun, et al. 2006. Electrical structures of the lithosphere along the Jiamusi massif and its eastern edge[J]. Chinese Journal of Geophysics (in Chinese), 49(2):598-603. |
| [13] | Liu Jian-xin, Gan Jia-xiong, Tong Xiao-zhong, et al. 2012. Finite element simulation and quailtative analysis of two-dimensional MT tipper response of tabular body[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 34(5):541-547. |
| [14] | Qiang Jian-ke, Wang Xian-ying, Tang Jing-tian. 2014. The geological structures along Huainan-Liyang magnetotelluric profile:Constraints from MT data[J]. Acta Petrologicca Sinica (in Chinese), 30(4):0957-0965. |
| [15] | Vozoff K. 1971. The effect of overburden on vertical component anomalies in AFMAG and VLF exploration; a computer model study[J]. Geophysics, 36(1):53-57. |
| [16] | Xi Zhen-zhu, Feng Wan-jie, Li Rui-xue, et al. 2011. Effect of a low-resistivity cover on high-frequency magnetotelluric sounding[J]. Geology and Exploration (in Chinese), 47(4):673-678. |
| [17] | Xiao Peng-fei, Bai Deng-hai, Varentsov, et al. 2010. Study on long-period magnetotelluric sounding——The LMT transfer function in eastern Tibetan plateau[J]. Seismology and Geology (in Chinese), 32(1):38-50. |
| [18] | Xiao Xiao, Tang Jing-tian, Zhou Cong, et al. 2011. Magnetotelluric sounding in the lujiang-zongyang ore-district and preliminary study of electrical structure[J]. Acta Geologica Sinica (in Chinese), 85(5):873-886. |
| [19] | Yang Zhen-wei, Zhang Kun, Yan Jia-yong, et al. 2012. A preliminary study on deep structure of Ning-wu ore district and its western marginal area[J]. Chinese J. Geophys. (in Chinese), 55(12):4160-4168, doi:10.6038/j.issn.0001-5733.2012.12.028. |
| [20] | Yu Nian, Wang Xu-ben, Kan Ai-ke, et al. 2007. Study on tipper and apparent tipper & application in fault interpretation[J]. Chinese Journal of Engineering Geophysics (in Chinese), 4(4):265-281. |
| [21] | Yu Peng, Wu Jian-sheng, Wang Jia-lin, et al. 2008. Long period magnetotelluric data-based study on deep fault structure in Shanghai and Zhejiang area[J]. Journal of Tongji University (Natural Science) (in Chinese), 36(4):549-554. |
| [22] | Yu Peng, Wu Jian-sheng, Wang Jia-lin, et al. 2008. Using long period magnetotelluric profile of Fengcheng of Shanghai-Huzhou of Zhejiang province to study deep electrical structure[J]. Chinese J. Geophys. (in Chinese), 51(2):503-510. |
| [23] | 安志国,底青云. 2006. CSAMT法对低阻薄层结构分辨能力的探讨[J].地震地磁观测与研究, 27(2):32-38. |
| [24] | 陈乐寿. 2009.大地电磁测深——探测地球深部电性和物质状态的一种有效手段[J].自然杂志, 31(1):39-46. |
| [25] | 陈乐寿,王光锷. 1990.大地电磁测深法[M].北京:地质出版社. |
| [26] | 陈清礼,胡文宝,李金铭,等. 2007.埋藏球体的倾子响应特征分析[J].石油天然气学报(江汉石油学院学报), 29(3):75-78. |
| [27] | 陈小斌,赵国泽,詹艳,等. 2004.磁倾子矢量的图示分析及其应用研究[J].地学前缘, 11(4):626-636. |
| [28] | 韩凯,刘国兴,韩江涛,等. 2012.乐昌-霞葛MT剖面深部电性结构研究[J].地球物理学进展, 27(3):997-1007, doi:10.6038/j.issn.1004-2903.2012.03.021. |
| [29] | 胡文宝,苏朱刘,陈清礼,等. 1997.倾子资料的特征及应用[J].石油地球物理勘探, 32(2):202-213. |
| [30] | 金胜,魏文博,叶高峰,等. 2009.班公-怒江构造带的电性结构特征——大地电磁探测结果[J].地球物理学报, 52(10):2666-2675, doi:10.3969/j.issn.0001-5733.2009.10.027. |
| [31] | 晋文光,孔祥儒. 2006.大地电磁阻抗张量的畸变与分解[M].北京:地震出版社. |
| [32] | 林昌洪,谭捍东,佟拓. 2011.倾子资料三维共轭梯度反演研究[J].地球物理学报, 54(4):1106-1113, doi:10.3969/j.issn.0001-5733.2011.04.026. |
| [33] | 刘国兴,张兴洲,杨宝俊,等. 2006.佳木斯地块及东缘岩石圈电性结构特征[J].地球物理学报, 49(2):598-603. |
| [34] | 柳建新,甘佳雄,童孝忠,等. 2012.板状体MT倾子响应的二维有限元模拟与定性分析[J].物探化探计算技术, 34(5):541-547. |
| [35] | 强建科,王显莹,汤井田,等. 2014.淮南-溧阳大地电磁剖面与地质结构分析[J].岩石学报, 30(4):957-965. |
| [36] | 席振铢,冯万杰,李瑞雪,等. 2011.低阻覆盖层对高频大地电磁测深的影响[J].地质与勘探, 47(4):673-678. |
| [37] | 肖鹏飞,白登海,刘美,等. 2010.长周期大地电磁测深研究——青藏高原东部LMT响应函数及应用[J].地震地质, 32(1):38-50. |
| [38] | 肖晓,汤井田,周聪,等. 2011.庐枞矿集区大地电磁探测及电性结构初探[J].地质学报, 85(5):873-886. |
| [39] | 杨振威,张昆,严加永,等. 2012.宁-芜矿集区及其西缘深部结构初探[J].地球物理学报, 55(12):4160-4168, doi:10.6038/j.issn.0001-5733.2012.12.028. |
| [40] | 余年,王绪本,阚瑷珂,等. 2007.倾子和视倾子的研究及在断裂解释中的应用[J].工程地球物理学报, 4(4):265-281. |
| [41] | 于鹏,吴健生,王家林,等. 2008.利用长周期MT数据研究沪浙地区深部断裂结构[J].同济大学学报(自然科学版), 36(4):549-554. |
| [42] | 于鹏,吴健生,王家林,等. 2008.上海奉城-浙江湖州长周期MT剖面揭示的深部电性结构[J].地球物理学报, 51(2):503-510. |
 2015, Vol. 30
2015, Vol. 30

