在众多的地面电磁勘探方法中,时间域电磁法具有分辨率高、抗干扰能力强和生产成本低廉等特点,在金属矿产、化石能源以及地热、工程和环境等领域的勘探中得到广泛应用.时间域电磁法的理论研究源于前苏联专家Kraev(1937)的研究,Wait(1951)的博士论文系统研究了地球介质的时间域电磁响应,Grant and West(1965)人进行了瞬变电磁测深的理论研究.由于时间域电磁方法的优点和应用前景,吸引了国内外同行的研究兴趣,理论和应用研究日趋活跃.70年代以来,随着理论研究的深入和电子信息技术的发展,针对不同的勘探任务发展了多种观测方式的时间域电磁方法理论和数字化的野外资料采集系统,如采用电型源或磁型源、长偏移距或共中心方式观测、地面、井地或井间观测方式等(Strack,1992;Wilt et al.,1995).
国内在时间域电磁法方面的理论和应用研究起步相对较晚(滕吉文,2006),20世纪70年代开始理论研究,80年代初期朴化荣等(1980)发表了关于大地上方时间域电磁响应的理论研究成果,推动了国内在时域电磁法方面的研究.瞬变电磁法在油气勘探中的应用到80年代后期才引起重视,随着信息技术的进步和发展,近年国内在时间域电磁法的理论和应用研究也取得了令人瞩目的成果.严良俊等人(2001)介绍了瞬变电磁法在南方灰岩山区油气勘探中的应用,薛国强等人(2007)介绍了国内外瞬变电磁理论与应用研究的进展.为了寻找便捷、高效的构造含油气性评价和开发油藏剩余油检测技术,需要改进常规瞬变电磁法的信号激励和信号采集技术,以在工业干扰严重的工区提高观测资料的信噪比.本文在Wang and Hohmann(1993)提出的时域有限差分算法的基础上,针对陆上采用大功率脉冲源激励时的特殊情况,研究了计算三维地球介质模型的时间域电磁响应的正演算法.
1 基本方程在准静态、线性和各向同性条件下,地球介质中的电磁响应满足麦克斯韦方程组.为了便于在数值模拟中实现对源的处理,将地层参数分别表示为背景参数(σb,μb,εb)和异常参数(σa,μa,εa)之和,将电磁响应表示为一次场(背景场)和二次场(散射场)之和,即

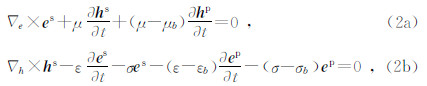
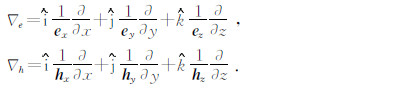
分别是考虑完全匹配层(PML)边界条件对电场和磁场的扩展算子,算子中的脚标 e和h 分别表示是对电场和磁场的作用.ei和hi(i=x,y,z)为坐标比例因子,分别是x,y,z轴上算子∇e和∇h的扩展变量.
求解(2)式的优点在于如果激励源远离异常电导率区域时,等效源相对于一个外加的偶极子会具有较为平滑的空间特性,这样当采用迭代方式计算区域内的场值时易于收敛.如果激励源位于异常体区域内,源附近的一次场值的空间变化非常剧烈,在网格剖分时需特殊考虑.
2 数值实现用差分代替微分是有限差分方法的基本出发点.首先将式(2)所表示连续形式的麦克斯韦微分方程组离散化,再用规则网格对地球物理模型进行剖分,最后用离散网格的差分替代微分,构造出求解电磁场响应的线性方程组.根据地球物理模型的特点,一般都采用非均匀的网格,在源或异常体附近网格采用较小的间距剖分,在远离源或异常体的地方可以适当加大网格间距,但网格间距的变化需满足收敛条件.
为了求解扩散方程,采用在可控源电磁响应正演计算中广泛使用的Yee元胞交错网格(沈金松,2003),如图 1所示.在Yee元胞的棱边上对电场进行采样,在每个Yee元胞每个面的中心对磁场进行采样.在对时间差分的步进计算中,由场在t0时刻的初始条件出发,按步距Δt交错进行电磁和磁场的计算.即在t=(n+1/2)Δt时刻,有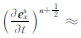
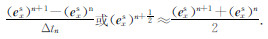
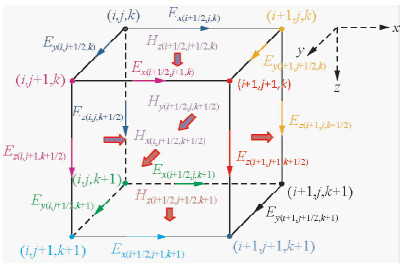 | 图 1 Yee元胞及场点定义 Fig. 1 Yee cell and involved fields of cross coupling |
这样,根据(2)式可以写出 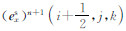 的差分表达式为
的差分表达式为
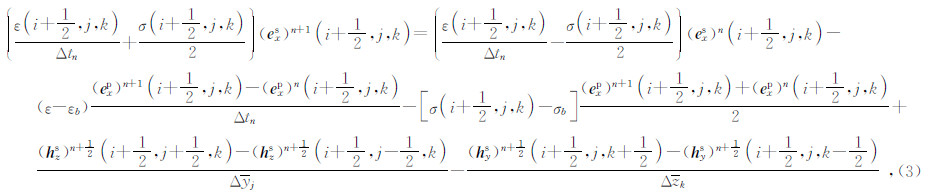

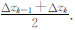 电场的其他分量具有类似的形式.
电场的其他分量具有类似的形式.
对于磁场,记t=nΔt时刻在(x,y,z)处的 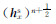
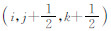 ,可得差分公式为
,可得差分公式为
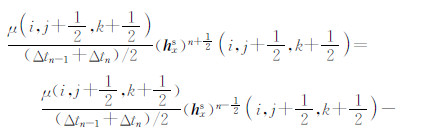

磁场的其他分量有类似的形式,此处不一一列举.值得指出的是,磁场满足无散条件(∇·b=0),磁场的三个分量中只有两个是独立的,另一个分量可由已知的两个分量中求得.
3 激励源和一次场按照(1)式所示的场的分解方案,可以将任何已知的源激励的场作为一次场,用于可控源电磁响应的计算具有很大的灵活性.本文考虑在长偏移距观测条件下接地导线源激励的情况,用电偶极子的场来近似.脉冲源的激励电流波形为拟高斯脉冲,其时间域表达式为

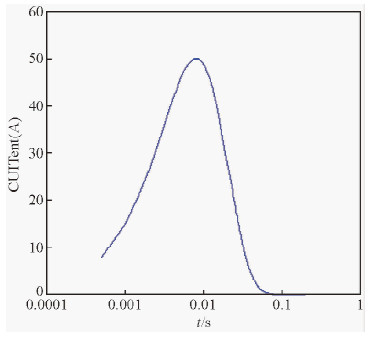 | 图 2 脉冲源激励电流波形 Fig. 2 Pulse of source current |

在计算一次场时,假定源位于均匀半空间地表的上方,源与地面的距离为h,源的中心设为坐标原点,如图 3所示.均匀半空间大地模型的电磁传输函数分三个区域进行计算,即源上方的空气中的场 e-、源与地面的空气中的场e+以及地面和地中的场e g.三维模型空间中任意点处传输函数的Ex分量的计算公式为
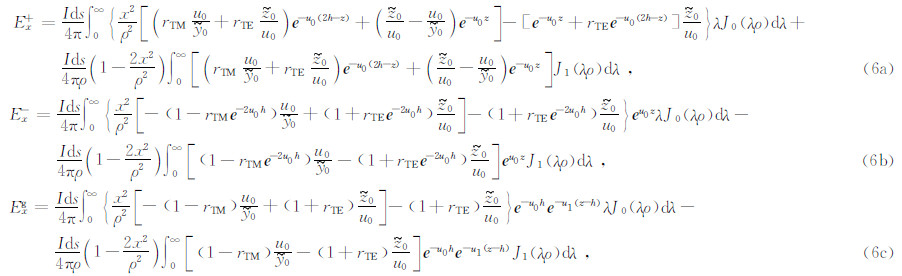
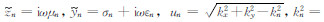
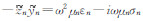 ,n=0表示空气介质,n=1表示地中介质.
,n=0表示空气介质,n=1表示地中介质. 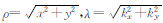 ,Jn为n阶贝塞尔函数,rTE和rTM分别为TE模式场和TM模式场的反射系数.其他分量的计算公式具有类似的形式,不一一列举.
,Jn为n阶贝塞尔函数,rTE和rTM分别为TE模式场和TM模式场的反射系数.其他分量的计算公式具有类似的形式,不一一列举.
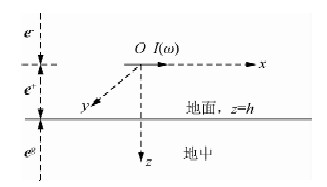 | 图 3 均匀半空间模型及一次场计算 Fig. 3 Primary field in homogeneous half space |
将(5)式所示的脉冲源频谱代入(6)式就得到了脉冲源激励时均匀半空间的频率域响应,再由频率域响应通过正弦变换得到时间域响应,即得到了三维模型的一次场分布.
4 FDTD算法验证为了检验算法的正确性,首先在电阻率为50 Ω·m的均匀背景介质的模型中,设计了一个层厚为200 m,顶面埋深为500 m的层状介质异常体,用所设计的三维FDTD算法计算其响应,对低阻层模型,该层的电阻率设为10 Ω·m,对高阻层模型,该层的电阻率设为100 Ω·m,计算响应的时间范围0.1 ms至1 s.将FDTD模拟结果与均匀半空间响应的解析解和层状介质模型响应的数字变换解的比较,以检查三维算法的正确性.图 4所示为低阻层模型响应曲线Ex分量的比较,图 5为同一测点处高阻层模型响应曲线的比较,蓝色曲线为均匀半空间的解析解,红色曲线为数值变换算法计算的结果,绿色曲线为利用FDTD算法计算的响应曲线.由图中可以看出,两种算法计算得到的响应形态基本一致,在数值上有些少许的差别主要源自于数值算法上的计算误差.
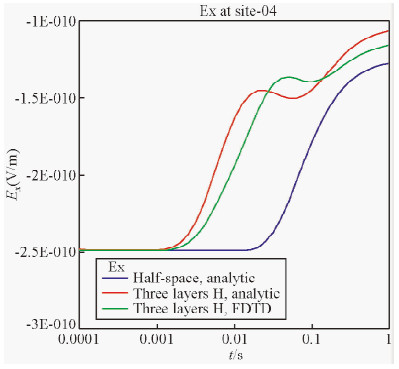 | 图 4 低阻层状介质模型的Ex响应对比 Fig. 4 Comparison of Ex responses in low resistive layer |
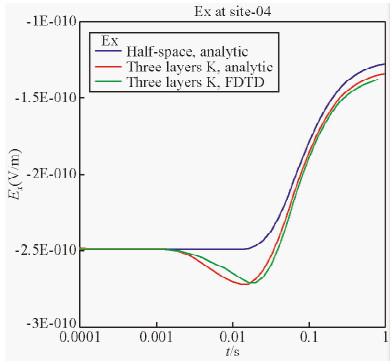 | 图 5 高阻层状介质模型的Ex响应对比 Fig. 5 Comparison of Ex responses in high resistive layer |
其次设置三维模型如图 6所示,在均匀半空间中放置一高阻长方体,异常体大小为6000 m×3000 m×200 m,顶面埋深为500 m,电导率为0.01 S/m.均匀半空间的背景电导率为0.02 S/m,测点位置(25,4000,0),计算瞬断响应,结果与积分方程计算结果对比如图 7所示,两条曲线形态基本一致.
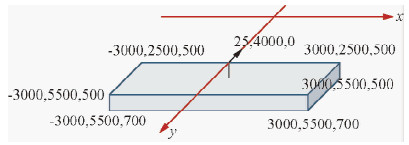 | 图 6 瞬断响应三维模型及参数 Fig. 6 3D model and parameters in under step response |
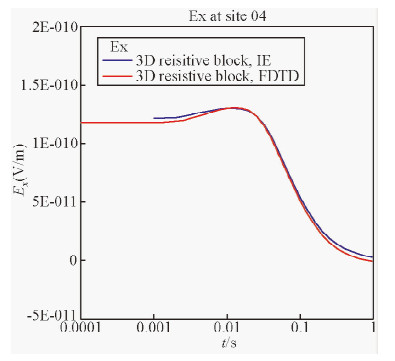 | 图 7 Ex瞬断响应对比 Fig. 7 Comparison of Ex responses between FDTD and integral equation algorithm |
设置三维模型如图 8所示,在均匀半空间中放置一高阻长方体,异常体大小为2000 m×1000 m×200 m,顶面埋深为500 m,电导率为0.02 S/m.均匀半空间的背景电导率为0.1 S/m,模型剖分范围为x=-6000~6000 m,y=-6000~6000 m,z=-100 m~5000 m,剖分网格数为50×75×30.电偶极脉冲源位于地表(0,0,0)处.时间域响应从t0=10-6 s至10-1 s.
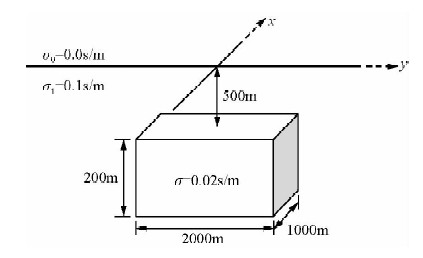 | 图 8 三维模型及参数设置 Fig. 8 Parameters in 3D model |
图 9所示为t=1 ms时地中400 m深处电场ex的总场分布图,由于场的幅值变化范围很大,绘图时取了幅值的对数,三维异常体的大小和位置如图中虚线框所示.由图中可以看出,ex总场的分布模式与电偶极源的场分布相同,可以清楚地分辨出场向外扩散的方式.
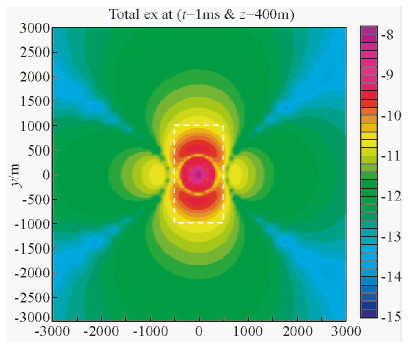 | 图 9 ex总场分布平面图(t=1 ms,z=400 m) Fig. 9 Distribution of total field ex |
图 10所示为t=1 ms时刻在y=10 m处x-z横截面上ex总场的分布图,注意在绘图时将z轴的坐标值取了负值,z=0处为地表,源位于(x,z)=(0,0)处.由图中可以看出,由于电磁场在空气层中的传播速度要远快于地中的场,地面上电偶极源的场的地中并不是以简单的半球状向地中扩散,而是大角度V形状向地中扩散.该时刻,脉冲源激励的场在异常体中已有显著的异常场产生,也就是说,该时刻的源场已达到异常体的埋深(500 m),并在异常体中感应出较强的二次场.如果按平面波的理论,此时刻的趋肤深度仅为大约50 m.此时异常体的总场与背景场显著不同,由异常场的分布基本能勾勒出异常体的边界.从图中还可以看出,此时刻的异常场本身作为二次场源向异常体周围扩散的情况.
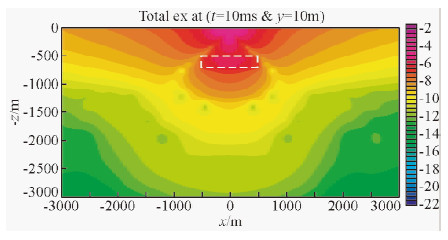 | 图 10 ex总场分布x-z剖面图 (t=1 ms, y=10 m) Fig. 10 Distribution of total field ex in x-z cross section(t=1 ms, y=10 m) |
随着时间的推移,脉冲源激励的场继续向地中扩散,图 11所示为当t=10 ms时刻ex总场分布的x-z截面图,此时刻脉冲源的激励电流为最大值.从图中可以看出,源场的主能量已达到超过1000 m的深度,异常体产生的异常场被淹没在一次场中,很难用肉眼识别出来.但异常场作为二次源在异常体周围产生的散射在地中深处还可识别出,可以看出此时散射场的空间波长要大于t=1 ms时的情况.如果将计算的各时刻场的分布连续显示,可以得到一次场向地中扩散以及异常体中二次场的变化并向地中再扩散的动画图像.
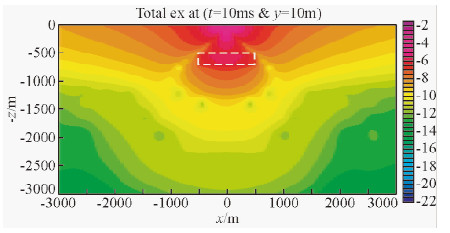 | 图 11 ex总场分布x-z剖面图 (t=10 ms, y=10 m) Fig. 11 Distribution of total field ex in x-z cross section (t=10 ms, y=10 m) |
采用基于非均匀步长交错网格的时域有限差分和非等时步长的迭代算法求解,从与层状介质的上阶跃响应对比结果以及与积分方程的瞬断响应结果对比,可以看出FDTD算法的计算结果基本正确,在此基础上计算了大功率脉冲源激励下晚时时域电磁响应,从结果上看异常场的特征比较明显,场的分布特征也能较准确反映出来.结果表明时域有限差分法数值模拟脉冲源激发的时间域电磁响应是稳定有效的,后续在计算速度上进一步提高后,可应用于时间域电磁响应的反演计算.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [1] | Grant F S, West G F. 1965. Interpretation Theory in Applied Geophysics[M]. New York:McGraw-Hill. |
| [2] | He Z X, Hu W B Dong W B. 2010. Petroleum electromagnetic prospecting advances and case studies in China[J]. Surveys in Geophysics, 31(2):207-224. |
| [3] | Kraev A P. 1937. Transient process in a homogeneous submerged medium[R]. Sci. Rep., Leningrad State Univ., No.14, Ser. Phys. Sci., Issue 3, Vol. 3. |
| [4] | Li Y, Wu X P, Lin P R. 2015. Three-dimensional controlled source electromagnetic finite element simulation using the secondary field for continuous variation of electrical conductivity within each block[J]. Chinese Journal of Geophysics (in Chinese), 58(3):1072-1087, doi:10.6038/cjg20150331. |
| [5] | Piao H R, Sha S Q, Wang Y L. 1980. Time domain electromagnetic response above the surface of a homogeneous earth[J]. Acta Geophysica Sinica (in Chinese), 23(2):207-218. |
| [6] | Shen J S. 2003. Modeling of 3-D electromagnetic responses in frequency domain by using staggered-grid finite difference method[J]. Chinese Journal of Geophysics (in Chinese), 46(2):281-288, doi:10.3321/j.issn:0001-5733.2003.02.024. |
| [7] | Strack K M. 1992. Exploration with Deep Transient Electromagnetic[M]. Amsterdam:Elsevier. |
| [8] | Teng J W. 2006. The development guide direction and locus of research manufacture and industrialization for the geophysical instruments and experimental equipments in China[J]. Geophysical Prospecting for Petroleum (in Chinese), 45(3):209-216. |
| [9] | Wait J R. 1951. The basis of electrical prospecting methods employing time varying fields[Ph. D. thesis]. Toronto:University of Toronto. |
| [10] | Wang T, Hohmann G W. 1993. A finite-difference, time-domain solution for three-dimensional electromagnetic modeling[J]. Geophysics, 58(6):797-809. |
| [11] | Wilt M, Morrison H F, Becker A, et al. 1995. Crosshole electromagnetic tomography:A new technology for oil field characterization[J]. The Leading Edge, 14(3):173-177. |
| [12] | Xue G Q, Li X, Di Q Y. 2007. The progress of TEM in theory and application[J]. Progress in Geophysics (in Chinese), 22(4):1195-1200, doi:10.3969/j.issn.1004-2903.2007.04.026. |
| [13] | Yan L J, Hu W B, Su Z L, et al. 2001. Electromagnetic exploration method and its application in the south carbonate rocks (in Chinese)[M]. Beijing:Petroleum Industry Press. |
| [14] | Yin C C, Zhang B, Liu Y H, et al. 2015. 2.5-D forward modeling of the time-domain airborne EM system in areas with topographic relief[J]. Chinese Journal of Geophysics (in Chinese), 58(4):1411-1424. |
| [15] | 李勇,吴小平,林品荣. 2015.基于二次场电导率分块连续变化的三维可控源电磁有限元数值模拟[J].地球物理学报, 58(3):1072-1087, doi:10.6038/cjg20150331. |
| [16] | 朴化荣,沙树琴,王延良. 1980.均匀大地上空的时间域电磁响应[J].地球物理学报, 23(2):207-218. |
| [17] | 沈金松. 2003.用交错网格有限差分法计算三维频率域电磁响应[J].地球物理学报, 46(2):281-288, doi:10.3321/j.issn:0001-5733.2003.02.024. |
| [18] | 滕吉文. 2006.中国地球物理仪器的研制和产业化评述[J].石油物探, 45(3):209-216. |
| [19] | 薛国强,李貅,底青云. 2007.瞬变电磁法理论与应用研究进展[J].地球物理学进展, 22(4):1195-1200, doi:10.3969/j.issn.1004-2903.2007.04.026. |
| [20] | 严良俊,胡文宝,苏朱刘,等. 2001.电磁勘探方法及其在南方碳酸盐岩地区的应用[M].北京:石油工业出版社. |
| [21] | 殷长春,张博,刘云鹤,等. 2015. 2.5维起伏地表条件下时间域航空电磁正演模拟[J].地球物理学报, 58(4):1411-1424. |
 2015, Vol. 30
2015, Vol. 30


