2. 西北有色地质勘查局物化探总队, 西安 710068
2. Team of Geophysical and Geochemical Exploration, Bureau of Geology for Non-ferrous Metals in Northwest, Xi'an 710063, China
不同类型地震波的极化特性不同,实际采集到的地震波是不同类型、不同极化特性的振动相互干涉和叠加的结果.极化分析是一种基于地震波的极化特性基础上的信号处理方法,通过测量各种类型地震波的极化属性实现多分量地震记录中各种重要信息的提取,在特定波型的识别与分离(Schimmel and Gallart,2003)、各类噪声压制、横波分裂分析(Helbig and Mesdag,1982;黄忠贤等,1994)、多波震相识别和确定波至到时(Bai and Kennett,2000;Reading et al.,2001;)等方面都有很好的效果.马见青对目前发展起来的各种类型的极化分析方法进行分析总结,包括其方法原理、各自的优缺点、应用范围、以及发展前景进行了详细总结(马见青等,2011).Vidale、Rene等和Li与Crampin定义了瑞利面波的瞬时极化分布并进行剪切波分裂分析,以上方法都是应用两分量地震数据,不能适用于更多分量数据处理(Vidale,1986;Rene et al.,1986;Li and Crampin,1991).Park提出了频率域极化分析方法(Park et al.,1987),陈赟对该方法进行了改进,提出了基于加窗Hilbert变换的频率域极化分析方法(陈赟等,2005,2007).Morozov提出了一种基于变分原理的极化分析方法,它适用于任意数目分量的地震数据处理,而且该方法可以利用瞬时极化分布进行地震波场分离和剪切波分裂分析(Morozov and Smithson,1996).上述方法有一个共同缺点是都在时间域或频率域中进行,当波形初至很接近时,再利用这种单一的时间域或频率域方法来刻画不同波型的极化分布就变得比较困难了.
为了解决这一难题,时频域极化分析的方法应运而生.Reading等按照Samson的方法设计了极化滤波器.该方法将傅立叶变换应用到三分量地震数据处理中,通过协方差矩阵计算每一个时窗内的特征值和特征向量,并利用这些特征值和特征向量在频率域中构造极化滤波器(Samson and Olson,1980,1981)).Diallo等将自适应瞬时极化滤波与时频分析相结合,对多分量地震数据进行小波变换,通过时频谱的实部和虚部来确定瞬时极化主轴、瞬时振幅、极化率等瞬时极化参数,再根据不同类型地震波的特定极化特性设计滤波器,进行面波压制、剪切波分裂研究以及转换波分离等(Diallo et al.,2005,2006a,b),它克服了单纯在时间域或频率域进行极化滤波时的不足,但是,该方法仍局限于二分量记录.
S变换(Stockwell et al.,1996;Pinnegar and Mansinha,2003)作为目前地震信号处理中广泛使用的一种时频分析方法,在时频域刻画信号频率的时变特征,特别适合解决在时间上重叠但有不同频谱的地震信号分离以及瞬时信号分析问题,同时避免了小波变换中尺度和频率之间的换算问题.本文在S变换基础上,提出了一种适合非平稳地震信号处理的广义S变换(GST),并将其引入到地震信号极化分析中.将Morozov提出的方法引入时频域,利用广义S变换,计算时频域瞬时极化分布,对多分量地震数据进行极化滤波.
1 GST基本理论地震信号u(t)的S变换为

本文在窗函数中引入一个以频率为自变量的调节函数,该时窗采用宽度可变的高斯函数为



通过设置调节因子,使得窗函数的宽度可以随信号频率呈线性或指数变化.这样,不仅能使窗函数的时宽随频率变化的速率变快,同时,窗函数时宽大小随频率的变化不再受线性变化的约束,这更符合非平稳地震信号的特点.实际应用中,一般选取a>1,0.5<b<1,c<2.
图 1是不同频率时S变换(1996)、广义S变换(2003)与本文提出的广义S变换窗函数的对比分析.可以看到,三种S变换的窗函数的宽度随频率的增大都在变窄,这也正是各种S变换的共性特征——频率越大,窗口越窄,时间分辨率越高.但是,本文提出的广义S变换与S变换、广义S变换窗函数相比,在低频段窗口宽度比S变换还宽,能得到较好的频率分辨率;在高频处的窗口宽度比S变换还窄,能得到较好的时间分辨率.
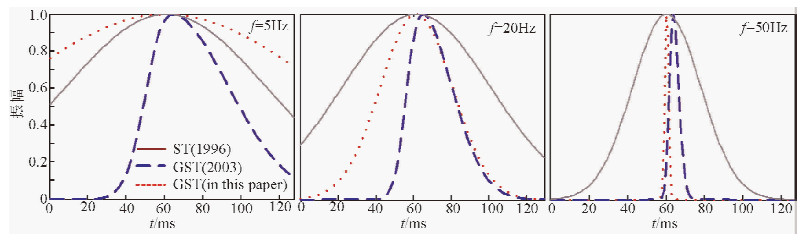 | 图 1 ST(1996)、GST(2003) 和GST(本文)的时窗函数对比 Fig. 1 The comparison of GST (in this paper), ST (1996) and GST (2003) |
对三分量地震数据 u(t)={ux(t),uy(t),uz(t)}Τ分别做广义S变换GST u(t,f),它包含uk(t)对应的广义S变换GSTuk(t,f).
由变分原理,求得时频域相位因子φ0(t,f)为


以下就是依据GST u(t,f)和φ0(t,f),得到的时频域极化椭球的瞬时矢量:极化主轴 R(t,f)、极化次轴 r(t,f),以及多分量数据的瞬时振幅 A(t,f)公式为


三维空间的椭圆形状是由主轴决定的,除了圆形的质点振动以外,因为圆形质点振动的情况有可能是噪声产生的一个假的主轴,为避免这个问题,Schimmel和Gallart(2003)定义了一个平面矢量 P(t,f):

对于圆形或椭圆振动,如果椭圆在同一个平面上,那么振动方向应该在同一个方向,为了追踪椭圆在三维空间内所处的位置,我们在每一个时频点(t,f)计算 P (t,f)与坐标轴X、Y、Z的夹角θx(t,f)、θy(t,f)和θz(t,f),公式为

利用 R(t,f)、r(t,f)、 P(t,f)和其他推导出来的极化参数,可以设计滤波器,对具有特定极化分布的波形进行分析和处理.
从方程(6)中,我们可以得到:

利用方程(10)、(11),我们就可以根据极化参数 R(t,f)、 r(t,f)和φ0(t,f)重新表达多分量信号的广义S变换GST u(t,f)为


为了直观理解时频域瞬时极化分析,现在通过对一个人工合成的三分量数据进行基于广义S变换的时频域瞬时极化分析,来实现不同波型波场分离的目的.图 2为人工合成的三分量数据(Diallo et al.,2005),主要包括(x-y)平面内的椭圆极化波(1~5 s)、(x-z)平面内的椭圆极化波(5~9 s)、(y-z)平面内的椭圆极化波(9~15 s)以及具有不同频率的线性极化波形和椭圆极化波的混合波(15~20 s).为了提取每一个坐标平面的椭圆极化波,我们根据每一组椭圆极化波的椭圆率和平面化向量来设计滤波器.
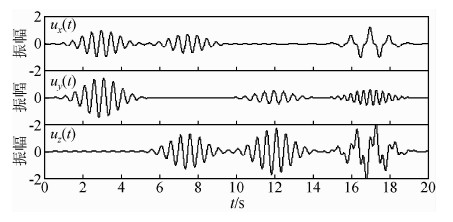 | 图 2 三分量合成信号(Diallo,2005) Fig. 2 Synthetic three-component signal(Diallo,2005) |
图 3为时频域中的瞬时极化分析过程.图 3a为时频域内的极化率分布ρ(t,f),图 3b-d为由极化主轴和极化次轴构成的平面矢量与坐标轴的夹角的时频分布θx(t,f)、θy(t,f)和θz(t,f),可以看出,对于A段波形,θz(t,f)=0;对于B段波形,θy(t,f)=0;对于C段波形,θx(t,f)=0.只有14~20 s之间的线性极化波在所有方向上,平面化向量P(t,f)都有非零值,而该时间段内的椭圆极化波的θy(t,f)=0.例如,为了分离(x-y)平面内的椭圆极化波,我们首先要在时频域识别θz(t,f)=0的区域.从极化参数的时频分布中可以看到:在1~5 s,θz(t,f)=0,可以确定该时段的波形为(x-y)平面内的极化波,与理论合成数据相符,该时间段的交互椭圆率也限定在一个特定的范围(ρ(t,f)  0.6,如图 3a所示).值得注意的是,在该时段是观察不到线性极化波的,这是因为该时段的交互椭圆率的时频域上的值为零(如图 3a的背景颜色所示).接着,将所识别出来的特定波形的 R(t,f)、 r(t,f)以及φ0(t,f)区域都设置为零,记为 R ′(t,f)、 r ′(t,f)和φ′ 0(t,f),并将其带入方程(10)和(11).最后,对方程(12)做广 义S反变换,得到滤波后期望得到的波.图 4为滤波后记录,图 5是滤波前后记录对比图.通过滤波前后的波形对比,可以看到本方法在多分量地震波波场分离及滤波中的效果.同理,我们可以按照极化参数在时频域中的分布情况,有选择性地提取特定时段的、具有特定极化特性的波形,显示了时频域瞬时极化分析的优越性.
0.6,如图 3a所示).值得注意的是,在该时段是观察不到线性极化波的,这是因为该时段的交互椭圆率的时频域上的值为零(如图 3a的背景颜色所示).接着,将所识别出来的特定波形的 R(t,f)、 r(t,f)以及φ0(t,f)区域都设置为零,记为 R ′(t,f)、 r ′(t,f)和φ′ 0(t,f),并将其带入方程(10)和(11).最后,对方程(12)做广 义S反变换,得到滤波后期望得到的波.图 4为滤波后记录,图 5是滤波前后记录对比图.通过滤波前后的波形对比,可以看到本方法在多分量地震波波场分离及滤波中的效果.同理,我们可以按照极化参数在时频域中的分布情况,有选择性地提取特定时段的、具有特定极化特性的波形,显示了时频域瞬时极化分析的优越性.
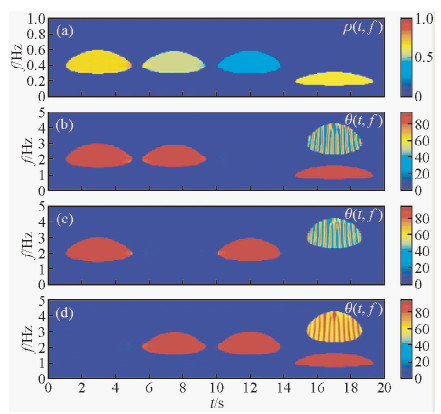 | 图 3 时频域瞬时极化参数谱 Fig. 3 Instantaneous polarization parameters spectrum in time-frequency domain |
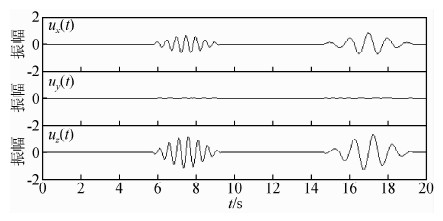 | 图 4 滤波后记录 Fig. 4 Multi-component signal after polarization filtering |
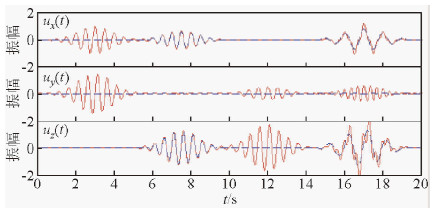 | 图 5 滤波前后记录对比图 Fig. 5 The comparison of raw multi-component signal between before and that after polarization filtering |
图 6为通过波动方程高阶交错网格有限差分方法正演模拟得到的双界面模型的三分量地震数据.采用中间放炮的方式,模型大小为1000 m×1000 m×1000 m,网格大小为dx×dy×dz=5 m×5 m×5 m,地震子波为雷克子波,主频为30 Hz,道间距为10 m.地层参数见表 1.
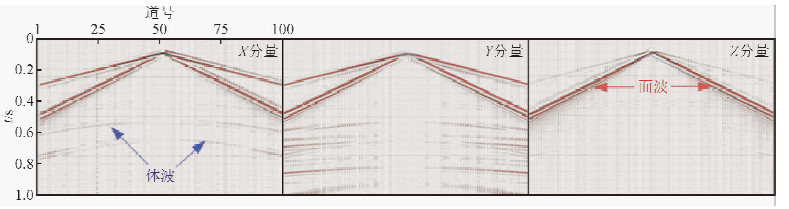 | 图 6 三分量模型地震炮记录 Fig. 6 Synthetic three-component seismic shot gather |
|
|
表 1 模型地层参数 Table 1 Stratum parameters of three- components seismic model |
图 7是原始炮记录中第5道信号各分量的时频谱.从时频谱中可以非常直观地看到具有强能量特性的面波的分布区域(800~1100 ms).图 8是瞬时极化率的时频谱.从极化率的时频谱中可以看到,在区域1内,极化率的值很低(小于0.25),该区域位于500~600 ms的范围,结合信号的时频谱可以确定,线性极化的直达波的极化率很小.区域2内,极化率的值很高(大于0.75),该区域位于800~1100 ms的范围,结合信号的时频谱可以确定,椭圆极化的面波的极化率很高.图 9是第5道数据的平面化向量与各坐标平面的夹角的时频谱θx(t,f)、θy(t,f)和θz(t,f).从这三张时频谱上同样能得到和极化率相同的规律.在区域2都存在不同强度的能量,这表明,面波在三个分量上都存在,这与三分量地震记录是相符合的.而且,面波在θx(t,f)、θy(t,f)和θz(t,f)上的能量不同,也就是说,面波的极化平面与三个坐标平面的夹角是不同的,说明了面波虽然在三个分量上都存在,但并不是均匀分布的,而是有所差别.
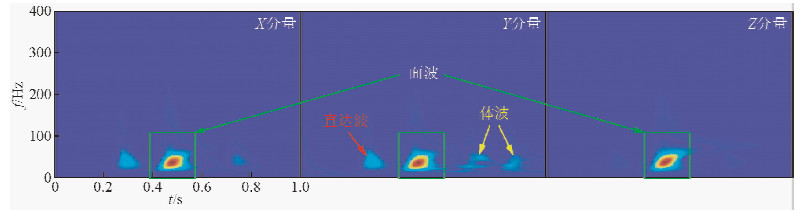 | 图 7 原始炮记录第5道信号的时频谱 Fig. 7 The time-frequency spectra of seismic signals before suppressing surface wave (the fifth trace) |
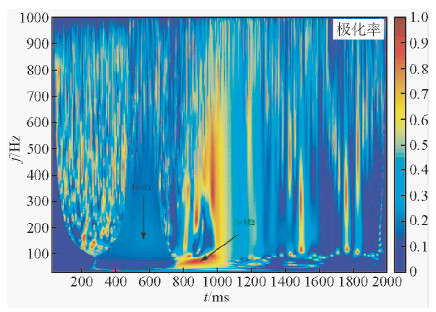 | 图 8 第5道数据的瞬时极化率时频谱 Fig. 8 The time-frequency spectra of the instantaneous polarization ratio before surface wave suppression (the fifth trace) |
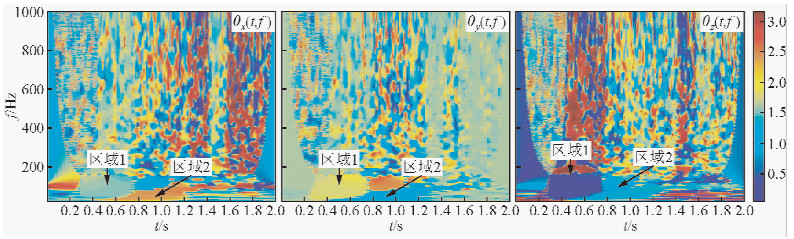 | 图 9 第5道数据的平面化向量与各坐标平面的夹角的时频谱 Fig. 9 The time-frequency spectra of the angle between planarity vector and each coordinate plane seismic signals before surface wave suppression (the fifth trace) |
图 10是用基于广义S变换的时频域瞬时极化滤波方法,通过椭圆率参数三分量记录进行面波压制.从滤波结果可以清楚的看到与瑞雷波相一致的低频、强能量的地震波得到了有效压制.图 11为利用时频域瞬时极化滤波方法进行面波压制前后的记录对比图.蓝实线表示原始信号,红虚线表示面波压制后的信号.从滤波前后的信号对比,可以很清楚地看到,在800~1100 ms之间分布的低频率、高振幅、强能量的面波被完全压制掉了,与此同时,其他有效波(500~600 ms之间的直达波以及面波之后出现的反射波)在滤波前后振幅没有发生任何改变.
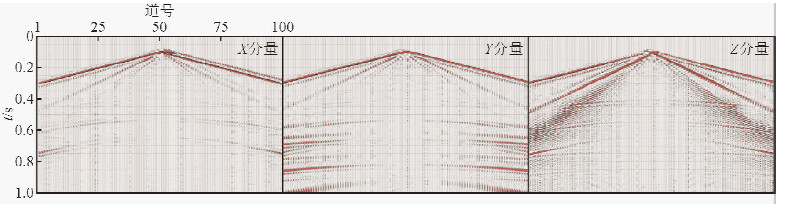 | 图 10 极化滤波压制地震面波后的三分量地震炮记录 Fig. 10 Three-component seismic shot gather after polarization filtering to suppress surface wave |
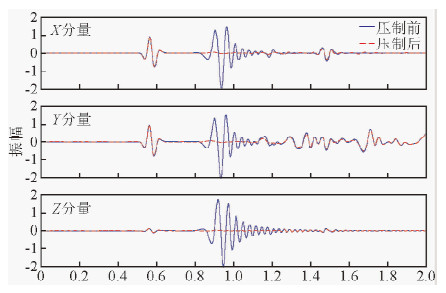 | 图 11 时频域瞬时极化滤波方法压制地震面波单道分析(第5道) Fig. 11 Single trace analysis of three-component seismic data before and after surface wave suppression based on the time-frequency domain instantaneous polarization method (the fifth trace) |
图 12是陕西省地震台网2002年记录的三分量爆破地震数据.该爆破记录在进行极化滤波之前做了随机噪声压制处理,这样能更加突出有效体波和面波.图 13是该实际资料的时频谱.从时频谱上能够清晰看到低频、高振幅、强能量的面波.
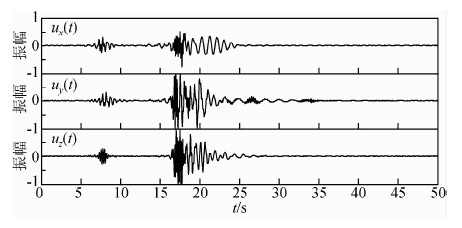 | 图 12 三分量实际台站地震数据 Fig. 12 The three-component station seismogram |
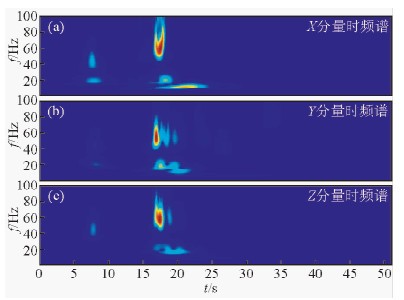 | 图 13 三分量数据的时频谱 Fig. 13 The time-frequency spectra of seismic signals |
图 14是通过极化分析得到的极化参数时频谱.图 14a是极化椭圆率时频谱,对于椭圆或圆形极化波,椭圆率比较大,接近于1;而对于线性极化地震波,椭圆率则很小,基本上接近于0.在极化率时频谱上可以推断,18~23 s的低频段存在高极化率的椭圆极化面波.根据极化率的大小,可以判断体波和面波,进而设计合适的滤波器分离或压制体波和面波.图 14b-d是平面化向量的方向余弦时频谱.通过该极化参数,可以判断时频谱中每一个时频点上的地震信号能量的方向.图 14b表示θx(t,f),图中区域1的波形频率低,对应于面波(18~23 s),θx(t,f)很大,接近于π/2,说明面波主要分布在(x-y)平面内.区域2显示的是频率较高,而且频带较宽的信号,主要分布在16~19 s,该区域的θx(t,f)很小,接近于0,属于线性极化波,结合原始数据时频谱,可以认定该区域的地震波属于体波.图 14c表示θy(t,f),与θx(t,f)相比,区域1和区域2的能量更强,表明面波分布的范围更宽.图 14d表示θz(t,f),与θx(t,f)、θy(t,f)相比,7~9 s处的低频强能量的信号消失,且16~19 s分布的面波频率较X、Y分量的高,表明Z分量的面波到时更晚,频率更高.综合图 14b-d可以看到:区域1的θx(t,f)和θy(t,f)很大,而θz(t,f)很小,这就说明椭圆极化的面波主要分布在(x-y)平面内;区域2的θx(t,f)很小,θy(t,f)和θz(t,f)都很大,这就说明线性极化的体波主要分布在Z方向.通过θx(t,f)、θy(t,f)和θz(t,f),很容易识别非平面波,进而可以设计滤波器压制这些非平面波.
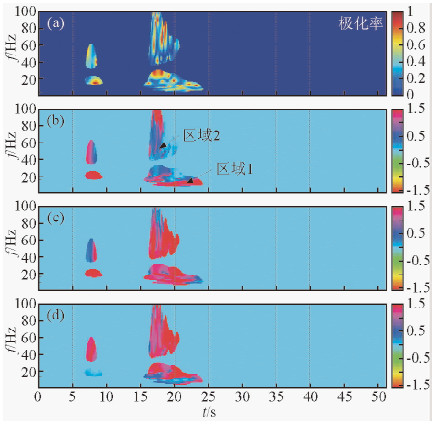 | 图 14 瞬时极化参数时频谱 Fig. 14 The time-frequency spectra of instantaneous polarization parameters |
图 15是利用极化参数ρ(t,f)、θx(t,f)、θy(t,f)以及θz(t,f)对图 12的三分量数据进行极化滤波处理的结果.为了压制(x-y)平面的面波,选择θz(t,f)值很小的区域,把该区域对应的R(t,f)、r(t,f)都设置为零,并将其带入方程(10)和(11).最后,对方程(12)做广义S反变换,得到滤波后的记录.通过该极化滤波之后,大部分的面波被压制.在20~25 s之间的水平分量上,仍有部分波存在,这些波除了含有部分面波外,还有可能存在P-SV转换横波.
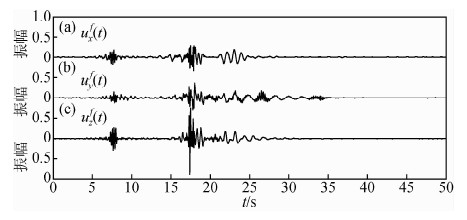 | 图 15 极化滤波重构记录 Fig. 15 The three component station seismogram after instantaneous polarization filtering |
5.1 本文实现了一种基于广义S变换的时频域瞬时极化分析新方法,并讨论了该方法在勘探地震和台站地震资料处理中的应用.
5.2 该方法在时频域中实现,结合了时频分析方法的优势.理论上,可以分辨具有不同极化性质的地震波,这些地震波可能在时间上重叠,在时频域中可以清楚地识别,在波形识别方面更加准确.
5.3 该方法首先计算多分量地震信号的时频谱和瞬时相位;然后,根据多分量信号的时频谱及瞬时相位计算极化参数,例如极化主轴、极化次轴、极化率、平面化向量等;最后,根据滤波目的,由这些极化参数设计合适的滤波器进行极化滤波.
5.4 通过极化率可以判断并分离线性极化波和椭圆及圆形极化波.
5.5 通过平面化向量与各分量之间的夹角大小,定性识别平面波和非平面波,并通过极化参数θk(t,f)(k=x,y,z)设计滤波器,进行非平面波压制.
5.6 由于特定波型在不同分量上的θ(t,f)不同,因此在实际处理中需要对每一分量设置相应的θ(t,f)值进行极化滤波,以实现特定波型的分离或压制.
5.7 极化分析方法除了在多波波场分离和去噪中具有优势以外,在横波分裂分析、多波震相识别等方面的应用都已经取得了成果.将来,极化分析方法在利用P波偏振资料或P波、S波联合偏振资料进行层析成像,确定速度异常的边界;在金属矿多波多分量地震及VSP领域中的应用研究等都是值得去探索的,这也为极化分析方法的发展提供了动力.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [1] | Bai C Y, Kennett B L. 2000. Automatic phase-detection and identification by full use of a single three-component broadband seismogram[J]. Bull. Seismol. Soc. Am., 90(1):187-198. |
| [2] | Chen Y, Gao L, Zhao F F. 2007. A method to enhance the signal/noise ratio of three-component seismic data based on the polarization analysis in frequency domain[J]. Progress in Geophysics (in Chinese), 22(1):255-261. |
| [3] | Chen Y, Zhang Z J, Tian X B. 2005. Complex polarization analysis based on windowed Hilbert transform and its application[J]. Chinese J. Geophys. (in Chinese), 48(4):889-895. |
| [4] | Diallo M S, Kulesh M, Holschneider M, et al. 2005. Instantaneous polarization attributes in the time-frequency domain and wavefield separation[J]. Geophysical Prospecting, 53(5):723-731. |
| [5] | Diallo M S, Kulesh M, Holschneider M, et al. 2006a. Instantaneous polarization attributes based on an adaptive approximate covariance method[J]. Geophysics, 71(5):V99-V104. |
| [6] | Diallo M S, Kulesh M, Holschneider M, et al. 2006b. Characterization of polarization attributes of seismic waves using continuous wavelet transforms[J]. Geophysics, 71(3):V67-V77. |
| [7] | Helbig K, Mesdag C S. 1982. The potential of shear-wave observations[J]. Geophys. Prosp., 30(4):413-431. |
| [8] | Huang Z X, Chen H, Wang G H, et al. 1994. Surface wave polarization and lateral heterogeneities of the lithosphere in China[J]. Acta Geophysica Sinica (in Chinese), 37(4):456-468. |
| [9] | Li X L, Crampin S. 1991. Complex component analysis of shear-wave splitting:theory[J]. Goephys. J. Int., 107(3):597-604. |
| [10] | Ma J Q, Li Q C, Wang M D. 2011. Review of multi-component seismic polarization analysis[J]. Progress in Geophysics (in Chinese), 26(3):992-1003. |
| [11] | Morozov I B, Smithson S B. 1996. Instantaneous polarization attributes and directional filtering[J]. Geophysics, 61(3):872-881. |
| [12] | Park J, Vernon F L, Lindberg C R. 1987. Frequency dependent polarization analysis of high-frequency seismograms[J]. J. Geophys. Res., 92(B12):12664-12674. |
| [13] | Pinnegar C R, Mansinha L. 2003a. The S-transform with windows of arbitrary and varying shape[J]. Geophysics, 68(1):381-385. |
| [14] | Pinnegar C R, Mansinha L. 2003b. The bi-Gaussian S-transform[J]. SIAM Journal on Scientific Computing, 24(5):1678-1692. |
| [15] | Reading A M, Mao W J, Gubbins D. 2001. Polarization filtering for automatic picking of seismic data and improved converted phase detection[J]. Geophysical Journal International, 147(1):227-234. |
| [16] | Rene R M, Fitter J L, Forsyth P M, et al. 1986. Multicomponent seismic studies using complex trace analysis[J]. Geophysics, 51(6):1235-1251. |
| [17] | Samson J C, Olson J V. 1980. Some comments on the descriptions of the polarization states of waves[J]. Geophys. J. Int., 61(1):115-130. |
| [18] | Samson J C, Olson J V. 1981. Data-adaptive polarization filter for multichannel geophysical data[J]. Geophysics, 46(10):1423-1431. |
| [19] | Schimmel M, Gallart J. 2003. The use of instantaneous polarization attributes for seismic signal detection and image enhancement[J]. Geophysical Journal International, 155(2):653-668. |
| [20] | Stockwell R G, Mansinha L, Lowe R P. 1996. Localization of the complex spectrum:the S transform[J]. IEEE Transactions on Signal Processing, 44(4):998-1001. |
| [21] | Vidale J E. 1986. Complex polarization analysis of particle motion[J]. Bull. Seismol. Soc. Am., 76(5):1393-1405. |
| [22] | 陈赟,张中杰,田小波. 2005.基于加窗Hilbert变换的复偏振分析方法及其应用[J].地球物理学报, 48(4):889-895. |
| [23] | 陈赟,高乐,赵烽帆. 2007.一种基于频率域偏振分析提高三分量地震资料信噪比的方法[J].地球物理学进展, 22(1):255-261. |
| [24] | 黄忠贤,陈虹,王贵华,等. 1994.面波偏振与中国大陆岩石层横向不均匀性[J].地球物理学报, 37(4):456-468. |
| [25] | 马见青,李庆春,王美丁. 2011.多分量地震极化分析评述[J].地球物理学进展, 26(3):992-1003. |
 2015, Vol. 30
2015, Vol. 30

