反褶积是地震资料最常用,最重要的处理方法之一,它可用于叠前和叠后地震资料处理.反褶积的主要作用是压缩地震子波,提高地震资料分辨率,从而提高地震资料解释的精度,为油田精细勘探和开发服务(黄绪德,1992).反褶积理论首先是由Enders Robinson提出的,后来他与Wiener、Norman、Levinson以及经济学家Paul Samuelson一起在麻省理工学院工作,并提出了反射地震的“褶积模型”(罗伯特等,1973).后来人们以该褶积模型为基础提出了很多常规反褶积方法.1954年,Robinson提出了预测反褶积,并在1967年发表文章详细论述了预测反褶积与维纳滤波的关系,认为预测反褶积包括脉冲反褶积,也是更广义的最小平方反褶积(谭军,2008).Taner和Cburn把地表一致性谱分解公式引入反褶积(Taner and Koehler,1981),Maurico和Danillo在频域做最小相位反褶积,Milton在1998年完成了混合相位反褶积等(凌云和周熙襄,1994).以上所述的反褶积方法主要在两个域实现:即时间域和频率域.这两类反褶积方法都是基于常规的褶积模型提出来的,有很多局限性,要求地震子波是稳定的,在传播过程中保持不变,没有考虑子波由于吸收衰减引起的变化.实际地震子波在地下传播过程中其能量、波形等是不断变化的,是一个动态过程.针对以上常规反褶积的缺陷,Gary Margrave教授在2002年提出了Gabor域的褶积模型.突破了传统的时间域和频率域的反褶积模式,在Gabor域实现衰减子波谱的估计,并求出反射系数.其具体方法是:对衰减地震记录的时频谱做平滑,去除反射系数的影响,从而实现衰减子波谱的估计.此方法在模拟记录和实际地震资料处理中都得到了很好的处理效果(Margrave et al.,2003;徐康,2005; Henley,2007;陈文超和高静怀,2007;高静怀和杨森林,2007).
非平稳地震记录的处理一般分为两类:直接的时变反褶积方法和反Q滤波方法(李振春等2014).针对第一类方法,Clark建立了时变的褶积模型,并且在时间域基于最佳Winner滤波进行反褶积(Clarke,1968).而对于反Q滤波方法,Bickle和Natarajan将反Q滤波看成是平面波域的反褶积(Bickel and Natarajan,1985);Hargreaves和Calvert认为反Q滤波是某一种形式的偏移(Hargreaves and Calvert,1991);Yanghua Wang在傅里叶域进行波场外推来解决反Q滤波的不稳定性问题(Wang,2002,2006).
本文采用S变换作为时频分析工具,因为S变换能够提供精细的时频谱,在地震数据处理中有着广泛的应用,如:地震记录的随机噪声衰减,面波压制,衰减参数提取等.将衰减的地震记录通过谱分解在S域进行分析,并提取震源子波和衰减参数Q,求取时变子波,再根据时变子波设计一个反算子,在S域对地震记录进行重构,再反S变换到时间域得到最终结果.其处理流程如下:
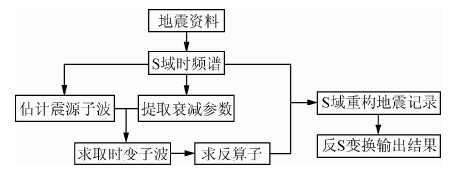 | 图 1 本方法的处理流程 Fig. 1 Flow chart of the processing method |
S变换是由Stockwell于1996年提出的一种加时窗傅里叶变换方法(高静怀等,2003;刘喜武等,2008;景建恩等.2012).其信号d(t)的S变换为

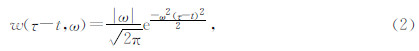
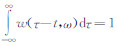 ,那么可以给出S反变换的公式为(杨林,2008)
,那么可以给出S反变换的公式为(杨林,2008)
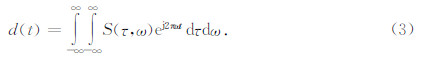
地震子波在地层中传播时需要一个合适的模型来描述地层对子波的吸收衰减作用,如果用褶积模型的观点来描述一维时间波场,那么地震记录的衰减模型实际上是子波的衰减模型.假设w(t,ω)表示t时刻的子波,经过了时间τ,子波变成了w(t+τ,ω),衰减因子为a(τ,ω).根据Hale理论(Hale,1982),可以建立出时变子波模型为
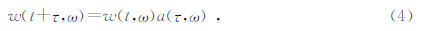


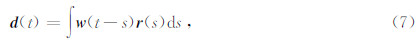
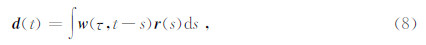

综上所述,震源子波、品质因子Q及反射系数序列生成一个由吸收衰减引起的衰减地震记录可表示为
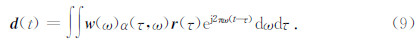
得到了时变子波 w(t+τ,ω)后,求它的振幅谱 A(τ,ω,x),由于吸收衰减作用,其振幅谱随偏移距x而变化.因此令
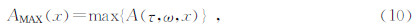
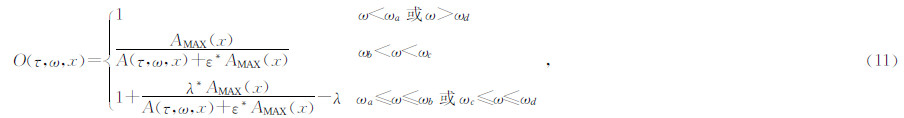

将地震记录的S谱S(τ,ω,x)与反算子O(τ,ω,x)相乘便可获得提高分辨率后的S谱,由S反变换可知,经下式便可得到提高分辨率后的输出结果,公式为
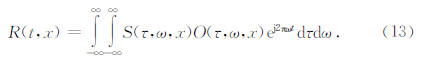
本文采用主频为30 Hz的雷克子波作为震源子波与模拟反射系数序列做一个常规的褶积模型(如图 2a所示),由于地层的吸收衰减作用,假设Q=35,根据公式(9)产生一个衰减的地震记录(如图 2b所示),图 2c是本方法处理后的结果.
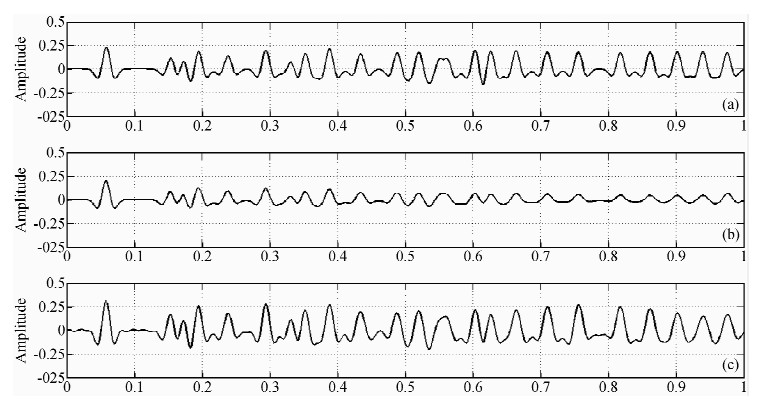 | 图 2 模拟数值试验: (a)平稳的合成记录;(b)衰减的合成记录;(c)本文方法处理后的结果 Fig. 2 Numerical simulation test: (a)Stable synthetic seismogram; (b)Attenuation synthetic seismogram; (c)Processing result from this method |
从以下模拟数据试验结果中可以看出,本方法对于吸收衰减地震记录,可以得到很好的处理效果.图 2b和图 2c的对比可以看到,处理后损失的能量得到明显的恢复,波形被压缩,分辨率在一定程度上得到了提高.本文方法考虑了子波的时变特性,把每一时刻的子波求出来再做反褶积.模型试算的结果证明了本方法适合处理衰减的地震记录,验证了本文方法的有效性.
为进一步分析本方法处理的处理效果,分别对处理前后的模型数据做S变换和傅里叶变换,并与原记录进行对比.图 3a、3b、3c是处理前后的时频谱,图 3d、3e、3f是处理前后的振幅谱.
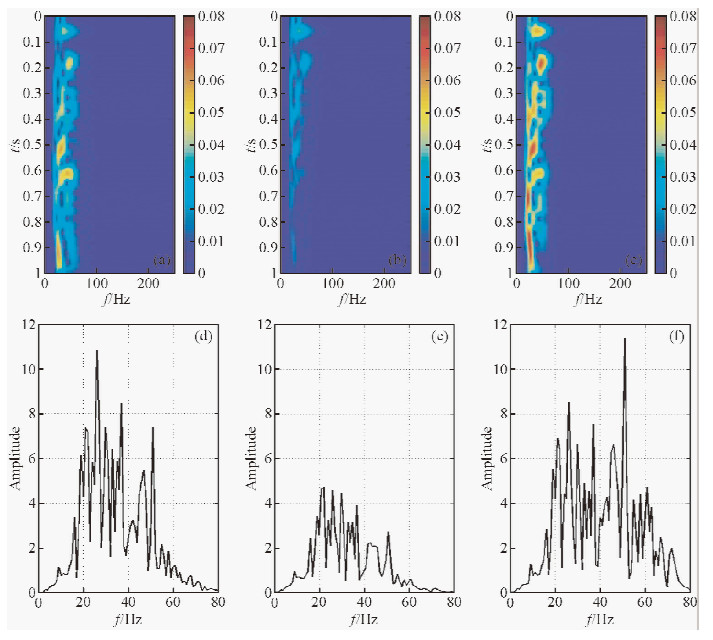 |
图 3 模拟数据试验的时频谱分析 (a)平稳记录的时频谱;(b)衰减记录的时频谱;(c)本方法处理结果的时频谱;(d)平稳记录的振幅谱; (e)衰减记录的振幅谱;(f)本方法处理结果的振幅谱. Fig. 3 Spectral analysis of numerical test (a)Time-frequency spectrum of stable data;(b)Time-frequency spectrum of attenuation data;(c) Time-frequency spectrum of processed data;(d) Spectrum of stable data;(e)Spectrum of attenuation data;(f) Spectrum of processed data. |
图 3a、3b、3c是处理前后的合成记录的时频谱,即S谱.从图 3b中可以看到,由于地层的吸收衰减作用,地震记录衰减明显,随着时间的增加,能量变低,频带变窄,主频也有所下降.图 3c是本方法处理结果的时频谱,通过对比图 3b和图 3c可以发现,损失的能量明显恢复,频带变宽,主频也得到了提高.图 3d、3e、3f是对合成记录处理前后的振幅谱,对比发现用本文方法处理后振幅基本上完全恢复,同时频带加宽,主频也提高了.通过频谱分析,进一步验证了此方法的有效性.
2.2 实际资料处理实际资料处理中,需要震源子波和Q值剖面.地震子波从地震记录的振幅谱|S(τ,ω,x)|中提取.地震记录中真实的震源子波是接近于零相位的(Dey,1999),因此把每一道的振幅谱算出来,并假设相位谱为零,通过傅里叶反变换,就得到了零相位震源子波(肖建华和孙文涛,1997; 戴永寿等,2007).但是由于相邻地震道的振幅存在差异,因此求得的子波在道与道之间显然也是不一样的,导致处理后的地震剖面同相轴连续性变差,达不到理想的效果.为了解决这个问题又不影响各道之间的频带变化趋势,对子波谱A(τ,ω,x)按下式进行多道加权平滑处理(梁光河,1998;赵秋亮,1998;赵秋亮等,2005),公式为
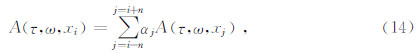
其中,n为加权窗的宽度,其取值不宜过大;αj是加权系数,其取值随|i-j|的增加而减小,两者间可以是线性关系也可以是非线性关系,若定义为线性关系,则:
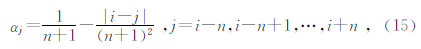
Q值剖面用经验公式提取,本文采用了综合考虑振幅和频率信息的峰值频率估算Q值法(张固澜等,2014),这种方法是对传统谱比法的有效改进,计算结果更加准确,适应性更强(高静怀和杨森林,2007),如图 4所示.
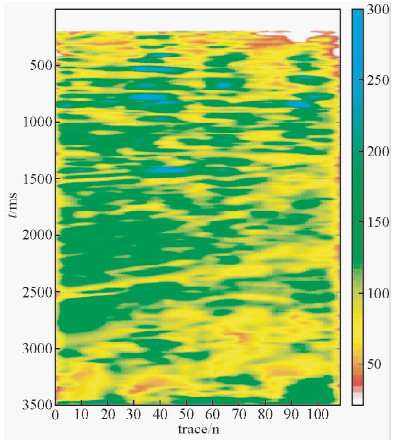 | 图 4 提取的Q值剖面 Fig. 4 Q value of seismic section |
图 5是某区叠后资料,共301道,2 ms采样,横轴表示道号,纵轴表示时间.从图中可以看出该地震剖面的分辨率相对较低.图 6是对图 5中的地震剖面处理后的结果.对比两图可以看出,本方法处理之后同相轴变细且连续性较好,分辨率得到提高,反射波组关系也有了明显的改善,验证了本方法在处理实际资料方面有很好的效果.
 | 图 5 原始地震剖面 Fig. 5 Original seismic section |
 | 图 6 本方法处理后的地震剖面 Fig. 6 Processed seismic section |
对比实际数据处理前后的振幅谱和S谱,如图 5所示.其中图 7a、7b分别为原始数据和本文方法处理后的振幅谱,从图中可以看出经过本方法处理后频谱都得到展宽.图 7c、7d分别为原始数据和本文方法处理后的S谱,从图中可以看出本方法都能拓宽地震记录的频带,对浅中深层频带能量的提升,深层能量改善明显.
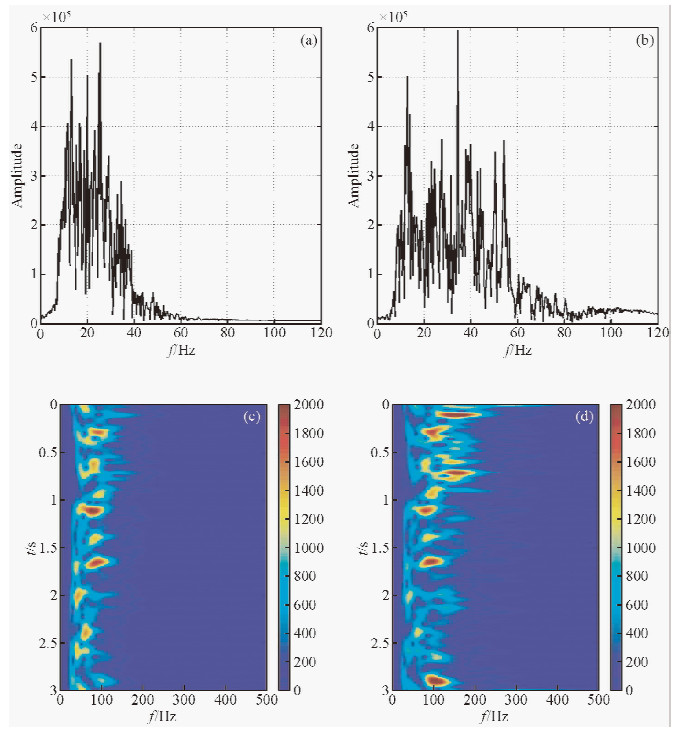 |
图 7 实际数据进行时频谱分析
(a)原始数据振幅谱;(b)本方法处理后的振幅谱;(c)原始数据时频谱;(d)本方法处理后的时频谱.
Fig. 7 Spectral analysis of original data (a)Spectrum of original data;(b) spectrum of processed data;(c) Time-frequency spectrum of original data;(d) Time-frequency spectrum of processed data. |
图 8是某区叠后资料,也是共301道,2 ms采样,2560个采样点.横轴表示道号,纵轴表示时间.图 9是对图 8中的原始地震剖面处理后的结果.对比可以看出,本方法处理之后同相轴变细且连续性较好,分辨率得到了明显提高.
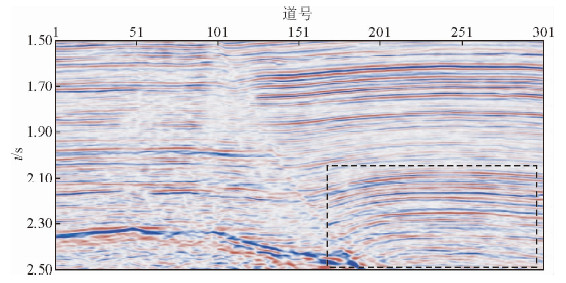 | 图 8 原始地震剖面 Fig. 8 Original seismic section |
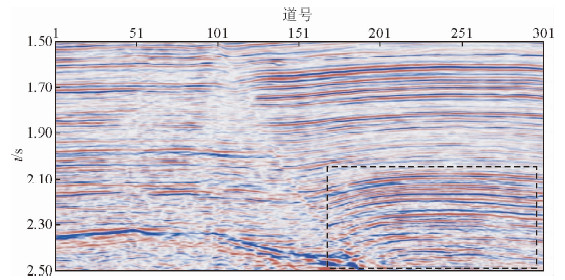 | 图 9 本方法处理后的地震剖面 Fig. 9 Processed seismic section |
为进一步对比分析本方法的处理效果,从实际资料中抽取第151道的地震记录进行对比并对其进行频谱分析.如图 10所示:
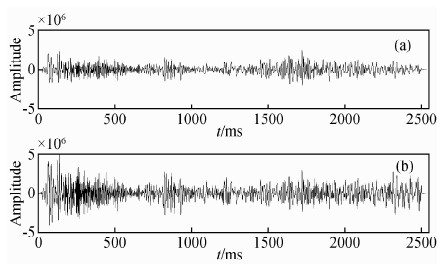 | 图 10 处理前(a)后(b)第151道的地震记录 Fig. 10 Seismic data of trace 151 before (a) and after (b) process |
从图 10中的第151道的地震记录对比可以发现,地震波损失的能量得到了恢复,尤其是深层部分的能量恢复的比较明显.这是因为地震波传播的越深,损失的能量越大.因为在深层部分处理效果比较理想.图 11是第151道的处理前后的频谱图,通过对比可以看出高频成分有所增加,频带得到了拓宽,主频也有了提高.进一步验证了本方法的有效性和实际应用性.
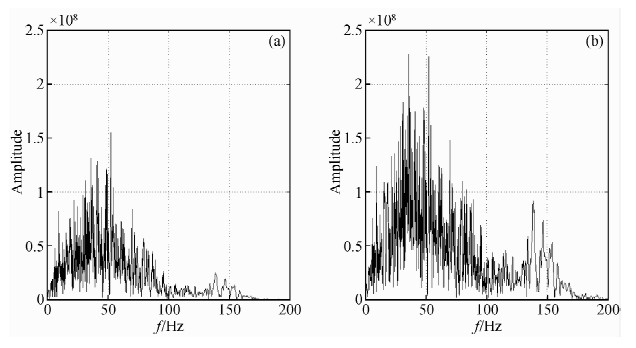 | 图 11 (a)原始数据振幅谱;(b)本方法处理后的振幅谱 Fig. 11 (a)Spectrum of original data;(b) Spectrum of processed data |
3.1 本文提出的提高地震分辨率的方法,是在S变换域进行震源子波的估计和衰减函数的估算,并由此建立时变子波模型,在S域求反算子并最终与原地震记录重构得到处理后的结果.本方法充分考虑了地层吸收衰减对子波的影响,体现了子波的时变特性,能把每一时刻的子波都估算出来,打破了常规反褶积中子波不变的局限性.处理之后的结果,能量得到了补偿,分辨率有了明显的提高.模拟数据和实际资料的测试结果都表明了本方法的可行性和有效性.
3.2 本文方法还有进一步的研究空间,因为本方法只考虑了子波波形随时间的变化,即时变特性,没有考虑子波的空变特性,即子波随空间位置的变化,这是我们下一步的研究目标.
致 谢 本研究由中海油提高地震分辨率处理技术研究项目(CJZB13096)资助,在此对参加项目的所有人员表示诚挚的感谢.| [1] | Bickel S H, Natarajan R R. 1985. Plane-wave Q deconvolution[J]. Geophysics, 50(9):1426-1439. |
| [2] | Chen W C, Gao J H. 2007. Characteristic analysis of seismic attenuation using MBMSW wavelets[J]. Chinese Journal of Geophysics (in Chinese), 50(3):837-843, doi:10.3321/j.issn:0001-5733.2007.03.024. |
| [3] | Clarke G K C. 1968. Time-varying deconvolution filters[J]. Geophysics, 33(6):936-944. |
| [4] | Dai Y S,Wang J L,Wang W W, et al. 2008. Seismic wavelet extraction via cumulant-based ARMA model approach with linear and nonlinear combination[J]. Chinese Journal of Geophysics (in Chinese), 51(6):1851-1859, doi:10.3321/j.issn:0001-5733.2008.06.027. |
| [5] | Gao J H, Chen W C, Li Y B, et al. 2003. Generalized S transform and seismic response analysis of thin interbeds[J]. Chinese Journal of Geophysics (in Chinese), 46(4):527-532, doi:10.3321/j.issn:0001-5733.2003.04.015. |
| [6] | Gao J H, Yang S L. 2007. On the method of quality factors estimation from zero-offset VSP data[J]. Chinese Journal of Geophysics (in Chinese), 50(4):1198-1209, doi:10.3321/j.issn:0001-5733.2007.04.029. |
| [7] | Hale D. 1982. Q-adaptive deconvolution:Stanford Expl. Proj. (SEP)[R] Report No 30, 133-158. |
| [8] | Hargreaves N D, Calvert A J. 1991. Inverse Q filtering by Fourier transform[J]. Geophysics, 56(4):519-527. |
| [9] | Henley D C, Margrave G F, Montana C. 2007. Gabor deconvolution:Surface and subsurface consistent[C]. CREWES Research Report, 19. |
| [10] | Jing J E, Wei W B, Chen H Y, et al. 2012. Magnetotelluric sounding data processing based on generalized S transformation[J]. Chinese Journal of Geophysics (in Chinese), 55(12):4015-4022, doi:10.6038/j.issn.0001-5733.2012.12.013. |
| [11] | Li H B, Zhao W Z, Cao H, et al. 2004. Characteristics of seismic attenuation of gas reservoirs in wavelet domain[J]. Chinese J. Geophys. (in Chinese), 47(5):892-898, doi:10.3321/j.issn:0001-5733.2004.05.022. |
| [12] | Li X Y, Wen H J, Chen S M, et al. 2013. Forward modeling studies on the time-frequency characteristics of isopachous thin interbedding[J]. Chinese Journal of Geophysics (in Chinese), 56(3):1033-1042, doi:10.6038/cjg20130331. |
| [13] | Li Z C, Guo Z B, Tian K. 2014. Least-squares reverse time migration in visco-acoustic medium[J]. Chinese Journal of Geophysics (in Chinese), 57(1):214-228, doi:10.6038/cjg20140118. |
| [14] | Liu X W, Zhang N, Gou Y F, et al. 2008. The comparison and application of time-frequency analysis methods to seismic signal[J]. Progress in Geophysics (in Chinese), 23(3):743-753. |
| [15] | Margrave G F, Long L, Gibson P C, et al. 2003. Gabor deconvolution:Extending wiener's method to nonstationarity[Z]. The CSEG Recorder, 28. |
| [16] | Taner M T, Koehler F. 1981. Surface consistent corrections[J]. Geophysics, 46(1):17-22. |
| [17] | Wang Y H. 2002. A stable and efficient approach of inverse Q filtering[J]. Geophysics, 67(2):657-663. |
| [18] | Wang Y H. 2006. Inverse Q-filter for seismic resolution enhancement[J]. Geophysics, 71(3):V51-V60. |
| [19] | Zhang G L, He Z H, Wang X M, et al. 2014. Seismic wave dispersion effects and inverse Q-filter phase compensation[J]. Chinese Journal of Geophysics (in Chinese), 57(5):1655-1663, doi:10.638/cjg20140528. |
| [20] | 戴永寿,王俊岭,王伟伟,等. 2008.基于高阶累积量ARMA模型线性非线性结合的地震子波提取方法研究[J].地球物理学报, 51(6):1851-1859, doi:10.3321/j.issn:0001-5733.2008.06.027. |
| [21] | 高静怀,陈文超,李幼铭,等. 2003.广义S变换与薄互层地震响应分析[J].015地球物理学报, 46(4):527-532, doi:10.3321/j.issn:0001-5733.2003.04.. |
| [22] | 高静怀,杨森林. 2007.利用零偏移VSP资料估计介质品质因子方法研究[J].地球物理学报, 50(4):1198-1209, doi:10.3321/j.issn:0001-5733.2007.04.029. |
| [23] | 黄绪德. 1992.反褶积与地震道反演[M].北京:石油工业出版社. |
| [24] | 景建恩,魏文博,陈海燕,等. 2012.基于广义S变换的大地电磁测深数据处理[J].地球物理学报, 55(12):4015-4022, doi:10.6038/j.issn.0001-5733.2012.12.013. |
| [25] | 李宏兵,赵文智,曹宏,等. 2004.小波尺度域含气储层地震波衰减特征[J].地球物理学报, 47(5):892-898, doi:10.3321/j.issn:0001-5733.2004.05.022. |
| [26] | 陈文超,高静怀. 2007.基于改进的最佳匹配地震子波的地震资料衰减特性分析[J].地球物理学报, 50(3):837-843, doi:10.3321/j.issn:0001-5733.2007.03.024. |
| [27] | 李雪英,文慧俭,陈树民,等. 2013.等厚薄互层时频特征的正演模拟[J].地球物理学报, 56(3):1033-1042, doi:10.6038/cjg20130331. |
| [28] | 李振春,郭振波,田坤. 2014.黏声介质最小平方逆时偏移[J].地球物理学报, 57(1):214-228, doi:10.6038/cjg20140118. |
| [29] | 梁光河. 1998.地震子波提取方法研究[J].石油物探, 37(1):31-39. |
| [30] | 凌云,周熙襄. 1994.可控震源自适应地表一致性反褶积方法[J].石油地球物理勘探, 29(3):306-315, 356. |
| [31] | 刘喜武,张宁,勾永峰,等. 2008.地震勘探信号时频分析方法对比与应用分析[J].地球物理学进展, 23(3):743-753. |
| [32] | 罗伯特 M,奥蒂斯,等. 1973.反褶积技术述评[J].石油地球物理勘探, 8(5):56-75. |
| [33] | 谭军. 2008.基于模型的变周期预测反褶积[硕士论文].青岛:中国海洋大学. |
| [34] | 肖建华,孙文涛. 1997.关于点爆炸震源产生的地震子波.石油地球物理勘探, 32(6):809-817. |
| [35] | 徐康. 2005.对提高反褶积处理效果的研究[硕士论文].北京:中国地质科学院. |
| [36] | 杨林. 2008.地震频谱分解技术应用中有关问题的讨论[J].石油物探, 47(4):405-409. |
| [37] | 张固澜,贺振华,王熙明,等. 2014.地震波频散效应与反Q滤波相位补偿.638/cjg20140528地球物理学报, 57(5):1655-1663, doi:10.. |
| [38] | 章珂,张学工,刘贵忠. 1998.一种新的地震子波估计方法[J].信号处理, 14(3):226-232. |
| [39] | 赵秋亮,李录明,罗省贤. 2005.基于分形方法的地震子波提取及应用[J].石油物探, 44(1):7-11. |
 2015, Vol. 30
2015, Vol. 30


