2. 中国科学院矿产资源研究重点实验室, 中国科学院地质与地球物理研究所, 北京 100029
2. Key Laboratory of Mineral Resources, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
在电法勘探中,往往通过引入比较简单的视电阻率定义公式,以便直观地解释地下电性界面的存在(电性参数、位置).然而,在瞬变电磁测深中,电磁响应是地电参数、收发距、时间等的复杂函数,难以求出大地电阻率与电磁响应的显式反函数,在定义视电阻率时不得不取某种极限以简化公式,得到远区或近区的视电阻率表达式.但在实际应用中,只有少数时间和收发距真正满足定义条件(汤井田和何继善,1994).这使视电阻率随时间和收发距变化的曲线发生畸变,不能客观反映地电断面的电性特征,给电磁测深的资料精细解释造成严重困难(刘建新,2013).为此,殷长春和朴华荣(1991)、黄力军(1995)、陈明生和田小波(1999)提出了运用数值逼近垂直磁场的方式定义视电阻率,由于该定义方式必须将磁场值按大小分成若干区间,然后进行分段级数逼近,从而得到视电阻率关于分段函数的表达式,步骤繁琐且容易造成畸变.白登海等(2003)提出的运用计算机迭代的方式对回线源瞬变电磁法进行全程视电阻率的提取.王华军(2008)依据均匀半空间瞬变电磁响应曲线随地下电导率、发射回线边长与观测时间具有平移伸缩特性,提出了一种直接计算回线源全程视电阻率的方法.杨海燕等(2010)对矿井瞬变电磁法全程视电阻率的解释进行了研究.Sheng(1986)等人尝试了用感应电动势数值求解全程视电阻率的方法,但是受到一定的限制.国内对于电性源短偏移瞬变电磁法刚刚起步,到目前为至,还没有一种比较完善的计算全程视电阻率的方法.
近年来,对B场响应的研究越来越受到人们的关注,Foley和Leslie(1998)、Purss和Cull(2003)、Annison(2004)、陈晓东等(2012)等先后对B场数据采集与应用进行了研究,并取得了良好的应用效果.特别是现在出现了商用化的B场观测装备,如SMART24 仪器.采用高性能磁通门磁探头,能够在野外直接测量出B场.这样,研究B场视电阻率计算具有重要的实际意义.由此本文讨论了基于垂直磁场Bz(t)的全程视电阻率响应,该视电阻率响应能够将远区和近区、中间区的视电阻率定义有机地统一起来.并避免了由感应电动势直接求取视电阻率存在二值性的问题,且能随电距离的变化,自适应地反映场的不同渐近特性,能达到直观地反映地电断面的垂向电性变化的目的.
1 电性源Bz与əBz/əT的响应比较由麦克斯韦方程组出发,经多种数学变换后可得到均匀半空间电性源瞬变电磁的磁感应强度垂向分量Bz(t)及其时间变化率əBz/ət表达式为(朴化荣,1990):
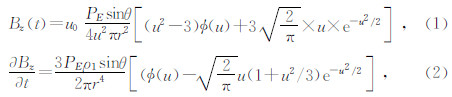
上式中,PE=IdL为电偶极子偶极距,Φ(u)=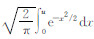 ,u=2πr/τ,称为感应系数,τ=2π
,u=2πr/τ,称为感应系数,τ=2π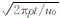 ,u0为真空中磁导率.
,u0为真空中磁导率.
分析公式(1)和(2)不难发现,它们都是关于电阻率ρ的复杂函数,且(2)式更是超越函数,目前数学上尚无法给出合适的反函数形式,因而利用其直接定义全程视电阻率存在困难,唯一的途径是采用数值求解法来完成.
分别研究Bz(t)和əBz/ət关于电阻率的变化关系可知,əBz/ət随电阻率的变化并非是一一对应关系,即对于一个给定的əBz/ət,一般有两个电阻率与之对应(图 1a).从而使数值求解视电阻率问题复杂化Yang Sheng(1986)提出了如何从两个电阻率中选取真值的规则,但是实用性较差,且有假极值现象存在.另外,在特定条件下还会出现无解情况.而Bz(t)随电阻率的变化关系是单调的一一对应关系(图 1b),这使得我们应用(1)式定义的全程视电阻率具有唯一性和可靠性.
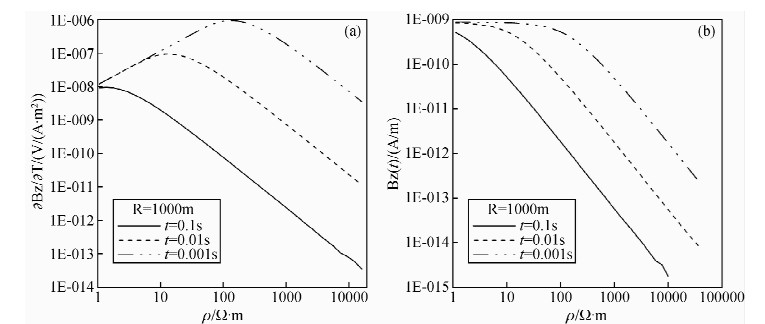 | 图 1 均匀半空间模型əBz/əT(a)和Bz(b)随电阻率的变化曲线对比图 Fig. 1 Contrastive curves of Bz and əBz/əT changing with resistivity ρ |
由均匀半空间电性源瞬变电磁的磁感应强度垂向分量Bz(t)的表达式可知,瞬变电磁磁感应强度垂向分量是电阻率ρ、时间t、磁导率μ0、以及观察点与源的相对位置r和的复杂函数.从(1)式可以看出,在瞬变电磁场感应强度垂向分量表达式中,r、t和ρ、μ0并不单独地影响场的性质,而是以u=2πr/τ的形式出现.因此我们不妨把(1)式变形为
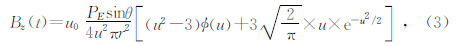
利用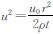 ,将其改写为
,将其改写为
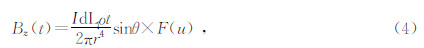
其中
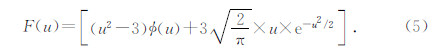
由(4)式可知,Bz与大地电阻率成正比,这也就是说Bz对地下的电性变化非常敏感.再令

由(4)、(5)、(6)式联立可得

分析上式不难发现,其为复杂的复宗量函数,直接进行电阻率的求解是非常困难的,随着计算机技术的高速发展,可采用迭代的方法进行求解.首先任取一个可能的电阻率值,将其与发送电流I、发射源长度dL、收发距r、方位角θ、及时间参数t等一同代入(3)式,编程计算,看与实测Bz对比相差多少.反复修改选取的ρ值,逐次迭代,直到得到的Bz与实测的Bz满足精度要求为止.
二分搜索算法是求非线性方程根的常用方法,因其算法稳定、易于实现而得到广泛的应用.张成范等(2009)、陈清礼等(2009)、刘俊等(2012)、李文尧和宴冲为(2013)等分别运用二分法对回线源全程视电阻率进行了定义,也都取得了一定的成果.根据Bz的单调性(如图 1b)可以采用二分法进行迭代电阻率ρ值的选取.使得计算速度更快、适应性更强. 3 磁感应强度Bz(t)的转换计算在实际勘探工作中,采用电偶源瞬变电磁测深时,一般观测二次场垂直方向变化在水平线圈中产生的感应电动势Vz(t),即磁感应强度垂向分量Bz(t)随时间的变化率əBz/ət乘以线圈参数(黄力军,1995).因此

式中sn为接收线圈的等效面积.采用积分方法可将其转换成磁感应强度的垂向分量Bz(t).根据电磁学原理可得
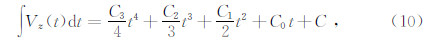
由于电性源瞬变电磁测深采样时间较宽,在计算磁场中应选计算精度高的计算方法,否则会造成误差累积,使电阻率曲线发生畸变.为了提高(9)式积分的计算精度,采用三次样条函数积分方法计算Bz(t).
即假定Vz(t)=C3t3+C2t2+C1t1+C0,然后采样三次样条拟合函数求解系数C3、C2、C1、C0.则积分形式为

将(10)式代入(9)式即可得到Bz(t).图 2为理论公式计算的均匀半空间磁感应强度垂直分量Bz与运用Vz(t)转换后的磁感应强度垂向分量的对比曲线,对比发现,此方法得到的磁感应强度的垂向分量与理论计算结果拟合性较好,平均相对误差为 1.63%左右.
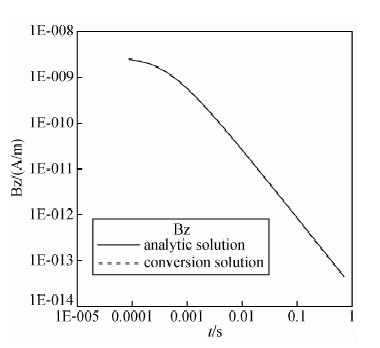 | 图 2 磁感应强度垂直分量理论计算与转换计算对比曲线 Fig. 2 Contrastive curves of Bz calculated value and theoretical value |
为了验证(7)式所定义的视电阻率形式是否适用,选取多种模型运用二分法计算并得到各地电模型视电阻率曲线图.图 3为利用二分法计算全程视电阻率流程图.图 4给出了均匀半空间条件下全程视电阻率曲线.地电参数ρ=100 Ω·m,场源dL=1000 m,收发距r=500 m,Φ=90°,I=10 A,运用二分算法对B-场数据进行全程视电阻率的求取.计算结果如图 4所示,对于均匀大地而言,视电阻率曲线为一水平直线,并且等于模型的真电阻率.
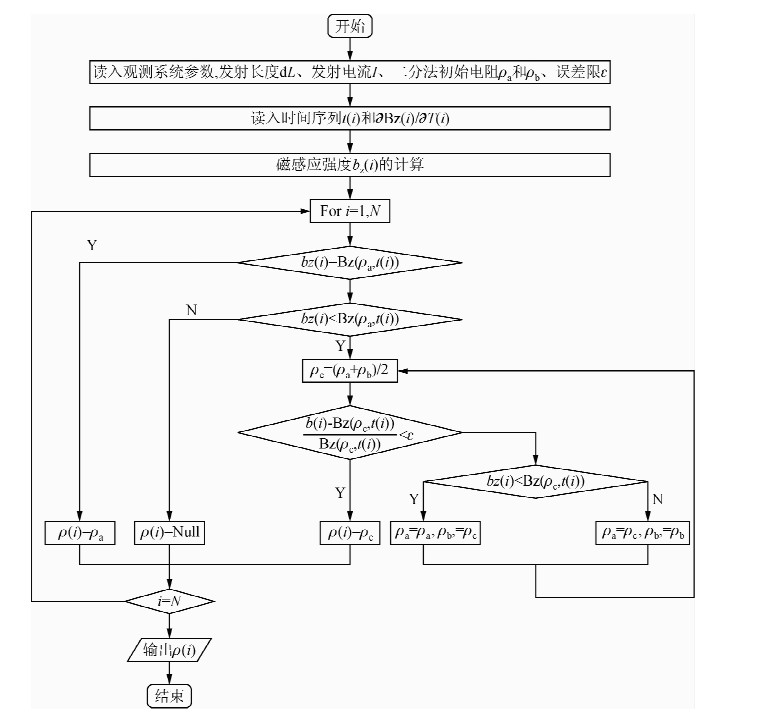 | 图 3 二分法计算全程视电阻率流程图 Fig. 3 Flow chart of binary search algorithm for calculating all-time apparent resistivity from əBz/əT |
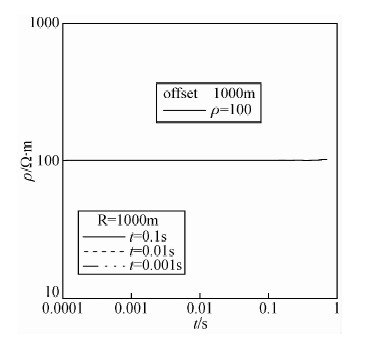 | 图 4 均匀半空间全程视电阻率曲线 Fig. 4 Apparent resistivity curves of homogeneous full space model |
与其他电磁测深方法一样,根据下层电阻率比上层电阻率高还是低,将B-场全程视电阻率曲线也分为两类.第一类ρ1<ρ2,称为高(G)型,第二类ρ1>ρ2,称为低(D)型.图 5是全程视电阻率两层曲线的理论量板.地电参数是ρ1=100 Ω·m,h1=200 m,ρ2/ρ1分别等于10、7、3、1、0.3、0.1、0.02,场源dL=1000 m,Φ=90°,I=10 A.由图可以看出,该视电阻率计算方法无论是在小偏移距(偏移距为500 m)或是在大偏移距(偏移距为2000 m)时都能很好的反映出地电模型的电性特征.
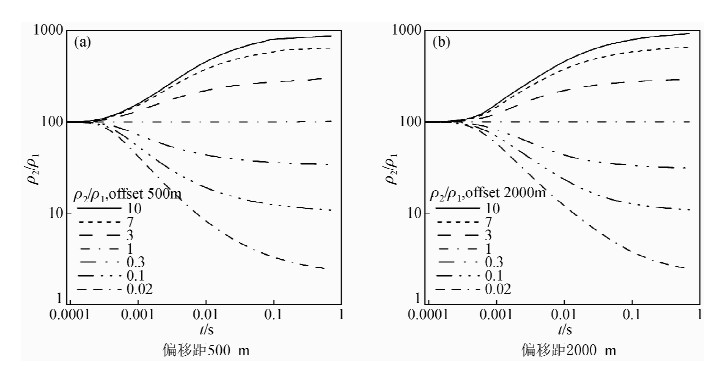 | 图 5 两层模型全程视电阻率曲线 Fig. 5 All-time apparent resistivity curve of the two layer model |
图 6为H型和K型地电模型,在中间层电阻率或中间层厚度发生改变时的全程视电阻率曲线对比.各电性层的地电参数如图中所示,发射源参数为dL=1000 m,Φ=90°,I=10 A.由图可知,该视电阻率计算方式都能明显的反映出三层地电结构.每一条测深曲线都能够较好的反映第一层电阻率,尾支趋近于第三层的真电阻率.综合比较两种地电断面可以看出,对于中间层的反映情况来说,K型断面,视电阻率曲线反映为向上的隆起.这个隆起的幅度以及范围,都没有H型地电断面全程视电阻率曲线的凹陷那么明显.但是都随着中间层厚度的加大,隆起或凹陷的幅度以及范围也变得越大.比较H型和K型的三层地电断面可以看出,高阻中间层的反映情况不如低阻中间层的好.这点对其他电磁方法也是一样的.
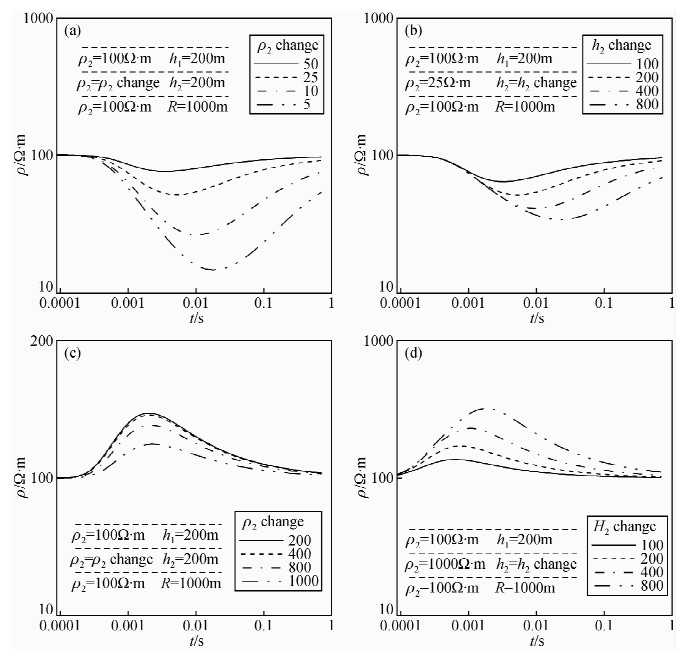 | 图 6 中间层电阻率不同和厚度不同全程视电阻率曲线对比 (a)H型地电模型;(b)H型地电模型;(c)K型地电模型;(d)K型地电模型. Fig. 6 Apparent resistivity curves comparison in resistivity or thickness of middle layer different |
图 7为不同偏移距、不同方位角全程视电阻率曲线对比,模型地电参数如图中所示,场源参数为dL=1000 m,Φ=90°,I=10 A.通过对比发现,不同偏移距或不同方位角下得到的视电阻率值差别很小,拟合程度较好.由于在计算时考虑了收发的几何关系,因此全程视电阻率计算方式消除了偏移距和方位角的影响.为资料的精细解释提供了保证.
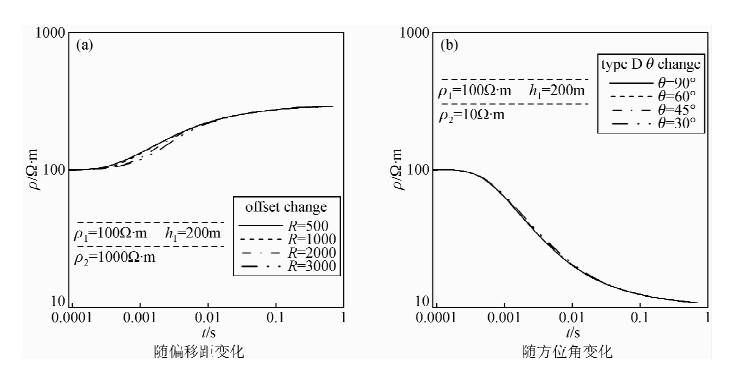 | 图 7 不同偏移距、不同方位角全程视电阻率曲线对比 Fig. 7 Apparent resistivity curve comparison at different offsets or azimuths |
勘探区所处大地构造位置为华北地台、内蒙古地轴、围场拱断束、克拉沁台穹,丰宁-隆化深大断裂从测区的南部通过;主要为太古代基地出露区,区内断裂发育,主要方向为北东向和近东西向,北西向次之.侵入岩发育,多为古元古代和中生代燕山期侵入.隆化县境内矿产资源丰富,大、中、小型矿床、矿化点星罗棋布;主要矿种有铁矿、铂、金、银、铜、铅、锌、磷、萤石、多金属矿等.代表性矿床有北岔沟门铅锌矿、韩麻营铁矿等.
勘探区内地层为太古界结晶基地出露区,区内仅出露晚太古界片麻岩及新生界第四系地层.区内构造位于丰宁-隆化深大断裂的的北侧,区内断裂构造发育,其方向为北东向和近东西向,北西向次之.规模从数百米到几公里不等,性质多为高角度平移断层,断距多为几百米,少数可达1000 m以上.区内发育一组北北西向断裂构造.区内岩浆活动强烈,岩浆岩大面积出露,种类繁多,其西北部为古元古代斑状二长花岗岩出露区,东南部为燕山期中细粒二长花岗岩(提云生等2011).本次勘探的主要任务是查明区内发育的北北西向高角度平移断层分布位置.根据断层电阻率异常的判定标准,可将横向视电阻率值线发生错断、有比较明显的密集梯度带或高阻与低阻之间呈现出明显的界限的地方定义为异常区的位置.也就是说在断层位置两侧电阻率有明显的差异.
采用V8多功能电法仪和SB-70k型探头(有效接收面积2000 m2)进行测试;选取发射线长度dL=450 m、发射电流I=10 A、偏移距r=475 m、点距为20 m、发射方向平行于测线方向、发射波形为TD50,发射频率为25 Hz.处理资料选自该区2线的测量结果,共29个测点,分别采用传统的晚期计算方式和Bz全期计算方式进行电阻率断面的对比.
图 8为传统的晚期方式定义的视电阻率与利用Bz计算的全程视电阻率所形成的断面图的对比.左图是采用传统的晚期数据计算的视电阻率断面,右图是利用Bz计算的全程视电阻率所形成的断面图.从图中可以看出,两种视电阻率断面存在明显的差异:首先,晚期视电阻率断面图在浅部也就是早期阶段全表现为高阻,远大于地层的实际电阻率值,而Bz全程视电阻率断面消除了浅部的假高值现象,相对真实的反映出了地层的电性变化规律;其次Bz全程视电阻率断面深部的电阻率信息也真实的反映了出来,与传统的晚期计算方式近似.根据断层电阻率异常的圈定原则,可分别在两种视电阻率断面的X方向480 m处推断为断层位置.从图中可以看出两种视电阻率计算方式的断面所推断的断层位置相当,但是Bz方式由于消除了浅部(也就是早期)的假高值现象,显示出来的效果更明显,且与该区已知的断层为高角度的平移断层信息相吻合.总的来说,实测数据表明利用Bz计算的全程视电阻率是正确的、有效的;且优于传统的晚期视电阻率计算方式.
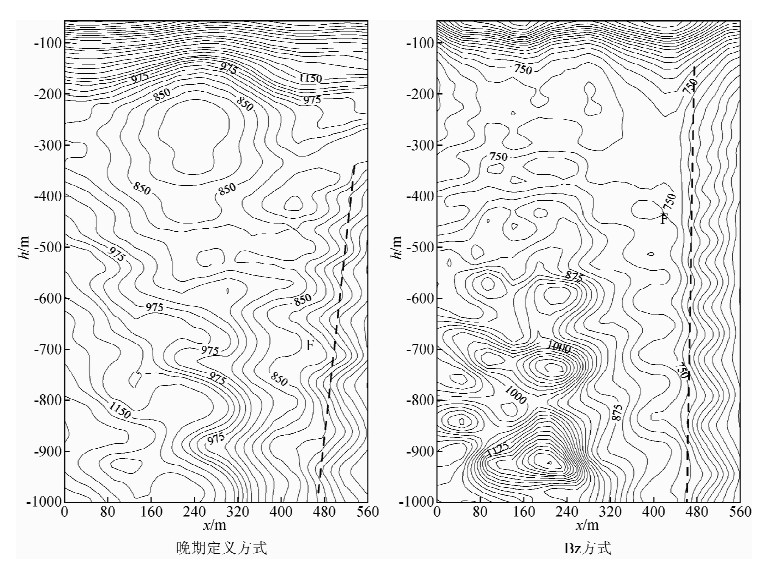 | 图 8 野外实测SOTEM两种视电阻率定义方式断面对比图 Fig. 8 Two kinds of apparent resistivity definitions section comparison chart of field SOTEM |
6.1 对电性源装置来说,利用磁感应强度的垂直分量本身定义全程视电阻率是单值且有解的,与用感应电动势(磁感应强度垂直分量的时间导数)相比,具有一定的优越性.
6.2 对于均匀半空间全程视电阻率响应曲线是一条直线,而对层状介质,曲线很好地反映了各电性层的真电阻率.对于多层介质的中间层,曲线反映良导层比高阻层效果好,即全程视电阻率有效地提取了地电断面的信息,电性分辨率高,分层能力强.
6.3 全程视电阻率仅与电性层的电性差异有关,基本与收发距无关,这样可以大大减少瞬变电磁测深理论曲线的计算工作,也很好地体现了瞬变电磁测深可采用小偏移距工作以减少野外劳动强度的优越性.
6.4 应用实例表明B-场全程视电阻率计算方式消除了传统晚期视电阻率计算方式造成的浅部假高值现象,相对真实的反映出了地层的电性变化规律.
致 谢 对课题组周楠楠博士在论文写作过程中给予的指导与帮助,以及本文匿名审稿人和编辑给予文章内容和格式上的帮助表示感谢!
| [1] | Annison C. 2004. B-Field TEM data acquisition for nickel exploration[C].// ASEG 17th Geophysical Conference and Exhibition-Extended Abstracts. |
| [2] | Bai D H, Meju M A, Lu J, et al. 2003. Numerical calculation of all-time apparent resistivity for the central loop transient electromagnetic method[J]. Chinese J. Geophys. (in Chinese), 46(5): 697-704, doi: 10.3321/j.issn:0001-5733.2003.05.018. |
| [3] | Chen Q Li, Yan L J, Fu Z H. 2009. Algorithm for the all-Time apparent resistivity of LOTEM method[J]. Chinese Journal of Engineering Geophysics (in Chinese), 6(4): 390-394. |
| [4] | Chen X D, Zhao Y, Zhang J, et al. 2012. The application of HTc SQUID magnetometer to TEM[J]. Chinese J. Geophys. (in Chinese), 55(2): 702-708, doi: 10.6038/j.issn.0001-5733.2012.02.034. |
| [5] | Foley C P, Leslie K E. 1998. Potential use of high Tc SQUIDS for airborne electromagnetics[J]. Exploration Geophysics, 29(2): 30-34. |
| [6] | Huang L J. 1995. A study of interpretation method for ondimensional full-region apparent resistivity of electric dipole source transient electromagnetic sounding[J]. Geophysical and Geochemical Exploration (in Chinese), 19(5): 391-397. |
| [7] | Li J S, Piao H R. 1993. On the calculation and application of the apparent resistivity of transient EM sounding by electric dipole[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 15(2): 108-116. |
| [8] | Li W Y, Yan C W. 2013. Bisection algorithm of central loop time domain transient electromagnetism all time apparent resistivity[J]. Journal of Kunming University of Science and Technology (Natural Science Edition) (in Chinese), 38(2): 26-33. |
| [9] | Liu J, Yang H Y, Lin Y. 2012. Binary search algorithm of all-time apparent resistivity in underground transient electromagnetic method[J]. Chinese Journal of Engineering Geophysics (in Chinese), 9(5): 526-530. |
| [10] | Purss M B J, Cull J P. 2003. B-field probes for down hole magnetometric resistivity surveys[J]. Exploration Geophysics, 34(4): 233-240. |
| [11] | Sheng Y. 1986. A single apparent resistivity expression for long-offset transient electromagnetics[J]. Geophysics, 51(6): 1291-1297. |
| [12] | Tang J T, He J S. 1994. A new method to define the full-zone resistivity in horizontal electric dipole frequency sounding on a layered earth [J]. Acta Geophysica Sinica (in Chinese), 37(4): 543-552. |
| [13] | Wang H J, Luo Y Z. 2003. Algorithm of a 2.5-Dimensional finite element method for transient electromagnetic with a central loop[J]. Chinese J. Geophys. (in Chinese), 46(6): 855-862, doi: 10.3321/j.issn:0001-5733.2003.06.020. |
| [14] | Wang H J. 2008. Time domain transient electromagnetism all time apparent resistivity translation algorithm[J]. Chinese J. Geophys. (in Chinese), 51(6): 1936-1942, doi: 10.3321/j.issn:0001-5733.2008.06.037. |
| [15] | Yan L J, Hu W B, Chen Q L, et al. 1999. The estimation and fast inversion of all-time apparent resistivities in long-offset transient electromagnetic sounding[J]. Oil Geophysical Prospecting (in Chinese), 34(5): 532-538. |
| [16] | Yang H Y, Deng J Z, Zhang H, et al. 2010. Research on full space apparent resistivity interpretation technique in mine transient electromagnetic method[J]. Chinese J. Geophys. (in Chinese), 53(3): 651-656. |
| [17] | Yin C C, Piao H R. 1991. A study of the definition of apparent resistivity in electromagnetic sounding[J]. Geophysics and Geochemical Exploration (in Chinese), 15(4): 290-299. |
| [18] | Zhang C F, Weng A H, Sun S D, et al. 2009. Computation of whole-time apparent resistivity of large rectangular loop[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 39(4): 755-758. |
| [19] | 陈明生, 田小波. 1999a. 电偶源瞬变电磁测深研究(四)——瞬变电磁测深视电阻率[J]. 煤田地质与勘探, 27(4): 52-54. |
| [20] | 陈明生, 田小波. 1999b. 电偶源瞬变电磁测深研究(五)——实测感应电压转换成垂直磁场[J]. 煤田地质与勘探, 27(5): 63-64. |
| [21] | 陈清礼, 严良俊, 付志红. 2009. 均匀半空间长偏移距TEM法全区 视电阻率的数值计算方法[J]. 工程地球物理学报, 6(4): 390-394. |
| [22] | 陈晓东, 赵毅, 张杰,等. 2012. 高温超导磁强计在瞬变电磁法中的应用研究[J]. 地球物理学报, 55(2): 702-708, doi: 10.6038/j.issn.0001-5733.2012.02.034. |
| [23] | 黄力军. 1995. 电偶源瞬变电磁测深一维全区视电阻率解释方法研究[J]. 物探与化探, 19(5): 391-397. |
| [24] | 李文尧, 晏冲为. 2013. 中心回线瞬变电磁法全期视电阻率的二分法求解[J]. 昆明理工大学学报(自然科学版), 38(2): 26-33. |
| [25] | 刘建新, 佟铁钢, 刘春明,等. 2013. E-Eφ广域视电阻率定义的改进 方法及场特性识别[J]. 中国有色金属学报, 23(9): 2359-2364. |
| [26] | 刘俊, 杨海燕, 林云. 2012. 地下瞬变电磁法全区视电阻率二分搜索算法[J]. 工程地球物理学报, 9(5): 526-530. |
| [27] | 朴化荣. 1990. 电磁测深法原理[M]. 北京: 地质出版社. |
| [28] | 汤井田, 何继善. 1994. 水平电偶源频率测深中全区视电阻率定义的新方法[J]. 地球物理学报, 37(4): 543-552. |
| [29] | 提云生, 刘长青, 夏春妹,等. 2011. 激发极化法在河北隆化县多金属矿区的应用[J]. 西部探矿工程, 23(5): 153-156. |
| [30] | 王华军, 罗延钟. 2003. 中心回线瞬变电磁法2.5维有限单元算法[J]. 地球物理学报, 46(6): 855-862, doi: 10.3321/j.issn:0001-5733.2003.06.020. |
| [31] | 王华军. 2008. 时间域瞬变电磁法全区视电阻率的平移算法[J]. 地球物理学报, 51(6): 1936-1942, doi: 10.3321/j.issn:0001-5733.2008.06.037. |
| [32] | 严良俊, 胡文宝, 陈清礼,等. 1999. 长偏移距瞬变电磁测深的全区视电阻率求取及快速反演方法[J]. 石油地球物理勘探, 34(5): 532-538. |
| [33] | 杨海燕, 邓居智, 张华,等. 2010. 矿井瞬变电磁法全空间视电阻率解释方法研究[J]. 地球物理学报, 53(3): 651-656. |
| [34] | 白登海, Meju M A, 卢健,等. 2003. 时间域瞬变电磁法中心方式全程视电阻率的数值计算[J]. 地球物理学报, 46(5): 698-704, doi: 10.3321/j.issn:0001-5733.2003.05.018. |
| [35] | 殷长春, 朴华荣. 1991. 电磁测深法视电阻率定义问题的研究[J]. 物探与化探, 15(4): 290-299. |
| [36] | 张成范, 翁爱华, 孙世栋,等. 2009. 计算矩形大定源回线瞬变电磁测深全区视电阻率[J]. 吉林大学学报(地球科学版), 39(4): 755-758. |
 2015, Vol. 30
2015, Vol. 30

