2. 塔里木油田勘探开发研究院, 库尔勒 841000;
3. 中国煤炭科工集团重庆研究院, 重庆 400039
2. Institute of Tarim Oilfield Company, Korla 841000, China;
3. China Coal Science and Industry Group Chongqing Institute, Chongqing 400039, China
致密砂岩油气藏做为一个新领域,有效预测储层的含油性非常困难(任青春等,2012).目前国内对致密砂岩油气藏的研究方法主要是采用叠前地震信息识别、地球物理测井和地震综合预测、叠后属性分析,采用叠前反演技术获得纵横波阻抗、泊松比和剪切模量等弹性参数,对储层的几何形状、物性和含流体性进行精细描述(王炳章等,2008;苏勤等,2011;张抗,2012; 李胜军等,2013).这些方法对致密砂岩岩性分布研究和砂岩油气藏类型研究有一定作用.但主要利用的是时间域的信息,且对由于砂岩非均质性、孔隙结构及流体的流动对信号的影响分析不够充分(刘兰锋等,2010; 李胜军等,2012).
众所周知,孔隙介质是由固体的骨架和孔隙构成的复合介质.岩石、陶瓷、超导材料等大部分是多孔介质.自1956年Biot提出孔隙弹性介质理论,开创了地震波在孔隙弹性介质中传播研究的先河(Biot,1956;赵海波等,2010).根据Biot理论,在地震频率范围(0~200 Hz)内,地震波在均匀孔隙弹性介质中传播是没有明显的衰减的.所以,地球物理学家一直在寻找其他理论解释实际地震数据和实验数据中观测到的高衰减产生机理.自20世纪70年代,已提出一些理论模型,如White的气泡模型,O’Connel等的喷射流模型、Pride等提出的多孔模型(O’Connell and Budiansky,1974;White,1975; Pride et al.,2004).
最近,在微尺寸(比孔隙大但比波长小)的不均匀介质中流体压力不同诱发的P波引起的流体流动,即微观机理,得到了广泛的关注.White等首先研究了微观机理,他们提出的气泡模型,水饱和与气饱和间隔的薄层模型,来解释地震频带内高衰减,这就是众所周知的White模型(Ren et al.,2008,2009).
Dutta等通过数值计算证实了White模型的精确性,他们认为气泡模型和薄层模型某种程度上是可比的(Dutta and Odé,1979).Gurevich等认为Biot衰减、散射、微观流体流动损失适用于一维薄层状孔隙弹性介质,并研究了垂直入射情况下的P波衰减(Gurevich et al.,1997; Zhao and Yang,2014).他们发现,微衰减机理衰减峰值比散射衰减峰值频率低.
本文在前人研究的基础上,通过数值模拟实验及物理模拟分析,证实了砂岩气藏在地震频带内地震波的衰减特征,定量的预测数衰减幅度,并将该项理论在中国石油的物探攻关区块进行了应用,取得了较好的应用效果.
1 方法原理及数值模拟当P波穿过孔隙介质时,一部分孔隙岩石被压缩,另一部分被扩张.如果岩石孔隙中是流体饱和的,压缩部分的孔隙压力要大于扩展部分的压力.若孔隙是连通的,流体将从高孔隙压力部分向压力小的部分移动.如果流体是黏性的,相对流体流动将导致能量损失.换句话说,波将衰减;另外,速度频散将产生(王大兴等,2006; 李胜军等,2008).
Biot理论模型指出在多孔弹性介质中有衰减和频散.在这个理论中,岩石骨架和流体的位移矢量分别由 u和U表示,孔隙流体相对于岩石骨架的位移用w表示(w =Φ(U-u)),这个根据介质的单位体积测量.对体积密度为ρb,孔隙度为Φ,渗透率为k的饱和岩石,孔隙介质的运动方程可写为
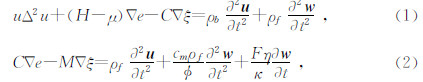
这里e= ▽ · u,ξ=- ▽ · w,ρb=ρg(1-Φ)+ρfΦ,ρg为矿物颗粒密度,ρf为流体密度,η为孔隙流体速度,cm为与孔隙结构相关的曲率参数,μ为饱和岩石的剪切模量.这里假定孔隙流体对剪切模量没有影响,因此,饱和岩石的剪切模量与干岩石的剪切模量是相同的.
根据Stern(1985),M、C和H是根据下式计算的弹性模量,公式为
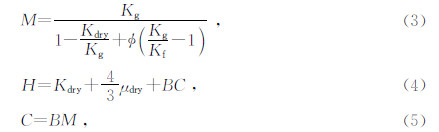
这里Kg,Kf,Kdry是矿物颗粒,孔隙流体和干岩石骨架的体积模量,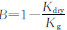 ,它通常叫Biot系数.最后,F是频率相关系数,它描述固体和流体间随频率增减的阻力,其表达式为
,它通常叫Biot系数.最后,F是频率相关系数,它描述固体和流体间随频率增减的阻力,其表达式为

这里T(ζ)是开尔文函数,其表达式为
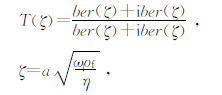
这里a是空隙大小因子,ω是角频率,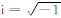 ,函数ber()和bei()是第一类贝塞尔函数,ber()和bei()是ber()和bei()函数的一阶导数(Dutta and Odé,1979; Masson and Pride,2010).
,函数ber()和bei()是第一类贝塞尔函数,ber()和bei()是ber()和bei()函数的一阶导数(Dutta and Odé,1979; Masson and Pride,2010).
为简单起见,考虑两种孔隙介质,厚度分别为d1和d2.这里d1和d2比地震波长小的多.这两种介质为(d1+d2)的层状周期排列,基于White模型,根据Carcione和Picotti(2006)针对P波垂直入射薄互层提出的复模量公式,推导可得薄互层的相速度Vp和品质因子Q为

这里Re(V)和Im(V)分别代表复速度V的实部和虚部,其中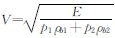 ,这里E为纵波的垂直穿过储层时的复数模量,也称为平面波模量,ρb1和ρb2分别代表介质1和2的体积密度.
,这里E为纵波的垂直穿过储层时的复数模量,也称为平面波模量,ρb1和ρb2分别代表介质1和2的体积密度.
垂直入射反射系数|NI|幅度和相位角为
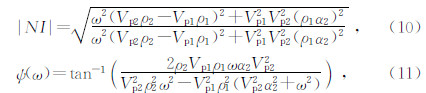
这里Vp和ρ分别代表垂直P波相速度和密度,角标1、2代表上下介质,油藏岩石的衰减系数与品质因子Q有关,公式为

孔隙介质的垂直相速度Vp和品质因子的倒数(1/Q)分别用式(8)、(9)计算.方程(10)~(12)中相速度Vp2可通过方程(8)计算,Vp1为上覆泥岩的纵波速度.层状孔隙介质的衰减通过公式(12)计算(Castagna et al.,2003 ;Korneev,2010; Quital et al.,2011; 张莹革,2014).
为了证明垂直入射的速度和相位角的频散效应,选择了两个油藏模型,代表通常油气勘探中遇到的类型.模型1代表压实的水饱和砂岩,模型2代表代表未压实部分气饱和砂岩气藏.模型1中的砂岩阻抗大于盖层的阻抗,含气砂岩阻抗低于盖层的阻抗.
砂泥岩参数采用Ren(2009)提供的参数,泥岩盖层纵波速度为2190 m/s,横波速度为820 m/s,密度为2.16 g/cm3,砂岩骨架纵波速度为4067 m/s,横波速度为2350 m/s,密度为2.65 g/cm3,流体纵波速度为1500 m/s,密度为1.02 g/cm3,通过改变砂岩气藏的含气饱和度来实现部分饱和与水饱和两种情况.根据上述公式(8)、(9)可以计算砂岩孔隙介质的相速度Vp和衰减系数1/Q与频率的关系,如图 1所示.从图 1a可以看出水饱和砂岩相速度随频率变化幅度较小,而部分气饱和砂岩气藏相速度在低频段变化较大,从0 Hz增加到22 Hz相速度的变化率达到13%,超过22 Hz以后,相速度随频率的增加变化趋势变的较为平缓;从图 1b中衰减系数随频率的变化关系中也可以较明显的看出,部分气饱和砂岩气藏在低频段衰减较严重,超过一个峰值之后衰减系数又变低,相对而言,水饱和砂岩衰减系数一直保持较小的数值,且基本随频率的增加没有变化.
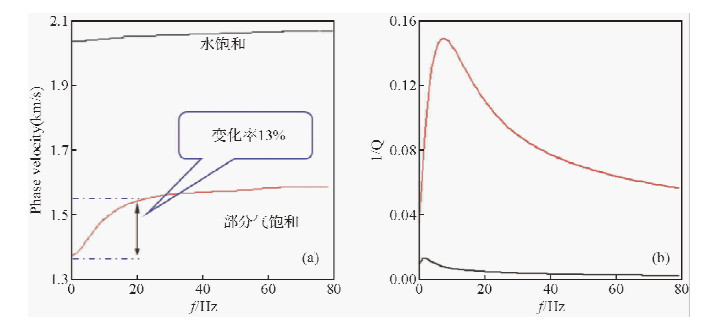 | 图 1 垂直相速度随频率的变化(a)与1/Q随频率的变化(b) Fig. 1 Vertical phase velocity varies with frequency(a) and 1/Q varies with frequency(b) |
利用公式(10)、(11)可以计算砂岩模型垂直入射情况下对应的反射系数和相位角随与频率的变化关系,如图 2所示.对于水饱和砂岩,相对反射系数和相位角随频率基本为发生变化,而部分气饱和砂岩,对反射系数和相位角影响较大,尤其是在低频端.频率从0 Hz增加到22 Hz,相对反射系数变化率达20%,同时相位角也发生了较大变化,超过峰值之后变化趋势都变的平缓.
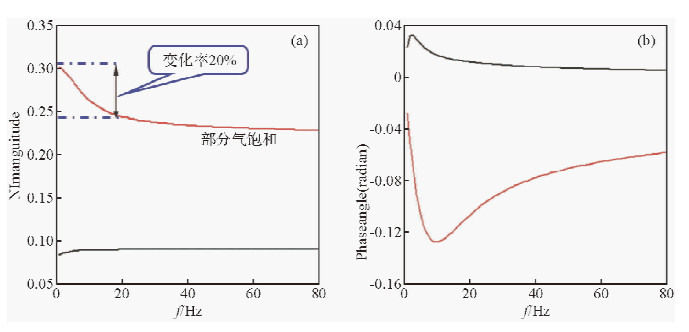 | 图 2 垂直入射反射系数数值随频率的变化(a)与垂直入射反射系数相位角随频率的变化(b) Fig. 2 The vertical incident reflection coefficient value varies with frequency(a) and vertical incident reflection coefficient phase angle varies with frequency(b) |
为了证实理论计算得到在低频端反射系数、相位、衰减变化的异常现象的正确性,针对上述模型开展了数值模拟实验研究.数值模拟时采用高阶精度的交错网格有限差分算法,尽可能的消除了由于差分引起的数值频散.地震子波选用Ricker子波,由于差分算法的限制,子波主频选在15~55 Hz,间隔为5 Hz,为了突出变化,在显示时以每10 Hz为间隔进行显示,结果如图 3所示.从图 3a中可以看出,对于部分含气砂岩模型,在低频15 Hz时振幅较强,在急剧减弱之后,振幅随频率的增加在缓慢减弱;相位也是在低频处呈异常,25 Hz之后基本稳定.对于饱和水砂岩模型计算结果如图 3b所示,可以看出,振幅和相位均未随频率的变化出现明显变化,与前面理论计算结果相吻合.理论分析和数值模拟实验都说明了砂岩在含气之后在低频端会产生振幅异常,也就是说通过频率域的分析可以有效检测砂岩层是否含气,进而实现储层的有效预测.
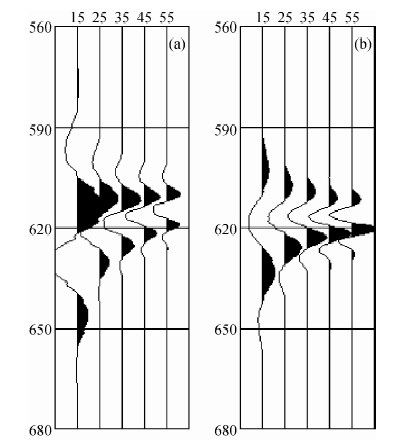 | 图 3 数值模拟不同频率的垂直入射记录 部分气饱和(a)与水饱和(b) Fig. 3 Vertical incident record of the different frequency part of gas saturation(a) and water saturation(b) |
理论分析及数值模拟实验结果都证实了部分含气砂岩在低频端有速度频散和振幅异常,但是理论假设是否正确,需要通过样品的测试进一步验证.为了研究砂岩孔隙样品在不同频率时是否有速度频散现象,测试时对样品使用了四种主频的纵波换能器进行波测试.测试前先对这四种频率的换能器在不同被测样品进行校正,以确定四个频率换能器之间是否存在测试差异.测试使用的换能器标称频率分别为1 MHz、0.5 MHz、0.25 MHz和0.1 MHz,这是岩石样品速度测试最常用的频率.但在实际测试时,由于被测样品的波阻抗等性能不同,得到的频率(主频)会有较大的不同,在高速且结晶较小的介质中测试时,得到的信号频率一般不会变化,但在粗晶砂岩和高衰减介质中得到的信号频率会有不同程度的下降.
为验证砂岩孔隙样品出现的速度随频率变化现象,选用了五种不同性能的材料作参考测试样品(图 4),一种是用硬铝(工业上常用的铝合金材料),此材料的阻抗和内部的结晶与高速的碳酸盐岩都相近.第二种是用环氧树脂与石粉混合而成的材料,用此材料的目的是,观测在制作人工砂岩中胶结物是否有频散现象.第三种是有机玻璃,其波阻抗与泥岩相近,而且内部均匀性和弹性都较好.另两块是不同粒径固结较好的天然砂岩,一块为粗颗粒与双孔隙样品相近,另一块为细颗粒.对这五种样品用上述四种换能器进行测试,观测不同频率时速度是否有误差.从已有的知识可知道,在铝合金或是有机玻璃上,只要样品的长度大于波长3~5倍时,其速度不会随测试频率面有的变化.但对于有一定孔隙度和颗粒的砂岩却有可能出现速度的变化.
 | 图 4 不同材料参考样品 Fig. 4 Samples of different material |
图 5~图 9给出了在五块参考样品上用四种频率测试的纵波波形,可以清楚地看到用四种频率测试对五种样品测试得到的波形.表 1为所测得的纵波速度.在图 5中铝样品的测试中,各频率得到的记录波形起跳时间基本一致,通过进行对零校正后速度的误差远小于1%,也就是说致密的铅块基本不存在速度的频散现象.
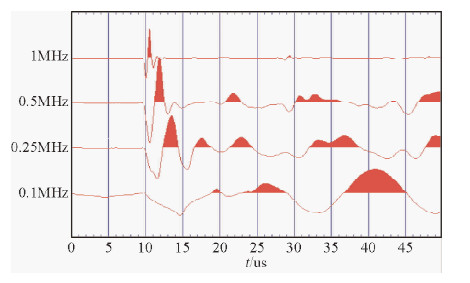 | 图 5 在铝样品上不同频率纵波透射记录 Fig. 5 Different frequency P wave transmission record on the aluminium samples |
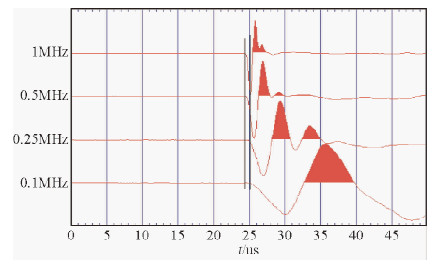 | 图 6 在石粉混合样品上不同频率纵波透射记录 Fig. 6 Different frequency P wave transmission record on the mixed stone powder samples |
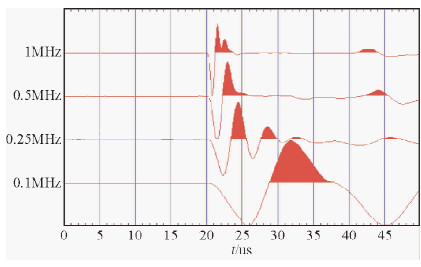 | 图 7 在有机玻璃样品上不同频率纵波透射记录 Fig. 7 Different frequency P wave transmission record on the plexiglass samples |
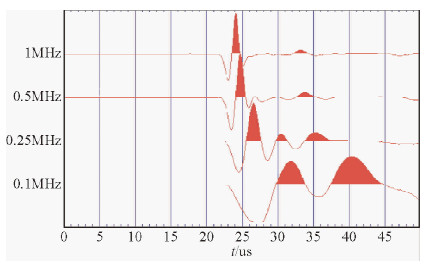 | 图 8 在粗砂岩样品上不同频率纵波透射记录 Fig. 8 Different frequency P wave transmission record on the coarse sandstone samples |
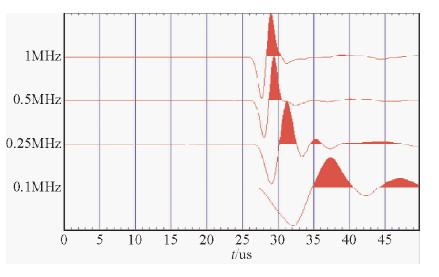 | 图 9 在细砂岩样品上不同频率纵波透射记录 Fig. 9 Different frequency P wave transmission record on the fine sandstone samples |
|
|
表 1 五块材料样品不同频率P波速度 Table 1 Five piece of material sample P wave velocity of different frequencies |
图 6和图 7分别是在石粉混合材料和有机玻璃上的纵波记录,可以看到当测试频率降低时,速度略有减小,但下降不到1%,小于0.5%,与测试误差相当.以上说明,在无孔的硬质材料用超声测试进行速度测试时,由测试频率引起的速度偏移小于0.5%.
图 8和图 9分别是在天然砂岩上测试的纵波记录,从记录的波形上可以明显见到,随着测试频率的降低波的传播时间增加,即速度减小,粗砂岩的速度下降比细砂岩速度下降程度大.粗砂岩纵波约有4.4%的误差,而细砂岩为3.4%.由于粗细砂岩的固结程度不同,这种速度随测试频度变化的原因应该就是样品颗粒和孔隙引起的.
通过五组物理模拟实验可以发现,样品的胶结程度(饱含气的程度)影响着速度随频率的变化,尤其对于粗砂岩样品的测试,由于胶结程度低,孔隙中含气,造成了速度的频散,证实了上面的理论分析的正确性.
3 实际应用实验工区位于新疆维吾尔自治区吐鲁番地区都善县境内,其包括温八、米登、温西一及温五四个区块,北临丘东凝析气田.其中温吉桑-温南区位于八道湾组和西山窑组煤系烃源岩两期供油范围内,煤成烃具有早生早排、富油富气的特征,具有充足的油气源,主要发育辫状河三角洲和扇三角洲,主要储集段为砂泥岩互层.区块内J1井,D2井都获得了良好的油气显示.
J1井目的层段为砂岩储层,日产气1.5万方、油11方,用S变换对井旁道进行时频分析,并显示出相应Xline线的单频剖面,如图 10所示.从图右侧岩性柱子可以看出,目的层段内为砂泥岩互层,但砂岩相对发育,从试气结果知道,该段基本为气饱和层段,含少量油和水,因为气泡存在,储层内会产生局部的压力差,在地震波传播过程中传过储层段时会产生压力差,引起所含流体相对骨架的运动,发生速度频散呈现出图 10所示明显的低频异常.W1井目的层段以泥岩为主,少量砂岩段无气显示,基本为水饱和储层,我们对该井井旁道进行S变换分析,时频图如图 11所示,可以看出目的层段内(图中层位之间),在21 Hz以内是根本没有低频异常的,也就是说无油气显示,与试气结果相一致.通过几口已钻井的验证,证实了本方法在实验区域的有效性,选择了适应的时频分析方法和最佳油气指示主频18 Hz,对整个工区的地震数据进行S变换,选择18 Hz的单频能量剖面,如图 12所示,在油气井位置均显示在较强的低频能量异常位置,同时配合地质分析及其他反演算法,多途径论证,为油田提供了5口建议井位,较好的完成了有利储层及流体预测目标.
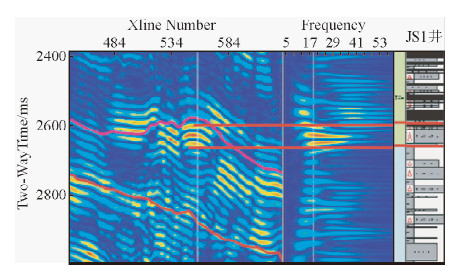 | 图 10 J1井井旁道分析结果 Fig. 10 Analysis result of J1 well |
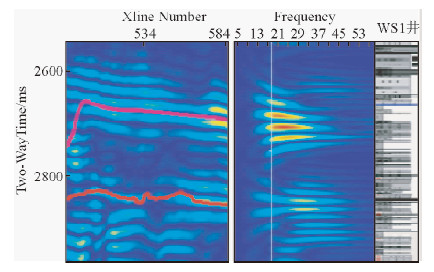 | 图 11 W1过井线时频分析剖面 Fig. 11 Analysis result of W1 well |
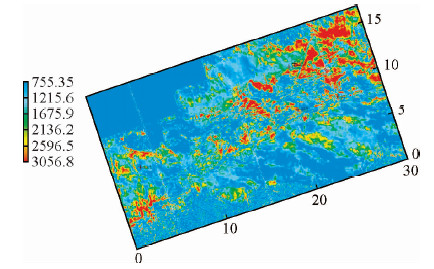 | 图 12 工区预测平面图 Fig. 12 Forecast result of work area |
4.1 对于未固结薄互层砂岩储层低频能量响应异常进行了分析,借助White模型,分别利用Biot理论、波场数值模拟方法,验证了水饱和及部分气饱和情况下,由于速度频散引起能量的差异,结果显示,部分气饱和砂岩储层,由于流体相对骨架的运动,对地震波的速度频散影响较大,而水饱和降低了储层的非均质性,因此速度频散较弱,相对而言低频能量异常也较弱.并利用天然砂岩制作了不同饱和度的砂岩模型,进行物理模拟分析,进一步验证了部分气饱和砂岩储层对速度频散的影响,揭示了利用地震低频能量异常可较好预测油气的规律.
4.2 利用地震低频能量异常检测油气的方法对吐哈物探攻关试验区块进行应用,对工区内油气井及水井进行分析,取得了非常高的吻合率,最后用该方法与其他储层预测方法相结合,对整个工区进行了储层及流体预测,取得了非常好的效果.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!
| [1] | Biot M A. 1956. Theory of propagation of elastic waves in a fluid-saturated porous solid:1-Low-frequency range[J]. The Journal of the Acoustical Society of America, 28(2):168-178. |
| [2] | Castagna J P, Sun S J, Siegfried R W. 2003. Instantaneous spectral analysis:Detection of low-frequency shadows associated with hydrocarbons[J]. The Leading Edge, 22(2):120-127. |
| [3] | Dutta N C, Odé H. 1979a. Attenuation and dispersion of compressional waves in fluid-filled porous rocks with partial gas saturation (White model); Part 1:Biot theory[J]. Geophysics, 44(11):1777-1788. |
| [4] | Dutta N C, Odé H. 1979b. Attenuation and dispersion of compressional waves in fluid-filled porous rocks with partial gas saturation (White model); Part 2:Results[J]. Geophysics, 44(11):1789-1805. |
| [5] | Gurevich B, Zyrianov V B, Lopatnikov S L. 1997. Seismic attenuation in finely layered porous rocks:Effects of fluid flow and scattering[J]. Geophysics, 62(1):319-324. |
| [6] | Korneev V. 2010. Low frequency fluid waves in fractures and pipes[J]. Geophysics, 75(6):N97-N107. |
| [7] | Li S J, Gao J H, Yong X S, et al. 2012. Spherical-wave AVO analysis of reflected P-wave[J]. Chinese Journal of Geophysics (in Chinese), 22(10):3459-3466, doi:10.6038/j.issn.0001-5733.2012.10.029. |
| [8] | Li S J, Gao J H, Zhang J D, et al. 2013. Volume texture attribute extraction technology and it's application[J]. Progress in Geophysics (in Chinese), 28(3):1563-1569, doi:10.6038/pg20130353. |
| [9] | Li S J, Sun C Y, Gao J H, et al. 2008. Analysis of dispersion suppression in wave equation numerical simulation[J]. Geophysical Prospecting for Petroleum (in Chinese), 47(5):444-448. |
| [10] | Liu L F, Cao S Y, Li X X, et al. 2010. Studies on the characteristics of low frequency seismic response from unconsolidated gas bearing sand reservoir[J]. Oil Geophysical Prospecting (in Chinese), 45(6):873-878. |
| [11] | Masson Y J, Pride S R. 2010. Finite difference modeling of Biot's poroelastic equations across all frequencies[J]. Geophysics, 75(2):N33-N41. |
| [12] | O'Connell R, Budiansky B. 1974. Seismic velocities in dry and saturated cracked solids[J]. Journal of Geophysical Research, 79(35):5412-5426. |
| [13] | Pride S R, Berryman J G, Harris J M. 2004. Seismic attenuation due to wave-induced flow[J]. Journal of Geophysical Research, 109(B1):B01201. |
| [14] | Quital B, Schmalholz S M, Podladchikov Y Y. 2011. Impact of fluid saturation on the reflection coefficient of a poroelastic layer[J]. Geophysics, 76(2):N1-N12. |
| [15] | Ren H T, Goloshubin G, Hilterman F J. 2008. Poroelastic analysis of amplitude versus frequency variations in thinly porous rocks[J]. SEG Technical Program Expanded Abstracts, 27(1):1744-1748. |
| [16] | Ren Q C, Wen Y H, Zheng L Q, et al. 2012. Prediction and hydrocarbon bearing measurement for tight sands reservoir based on pre-stack inversion[J]. Tuha Oil & Gas (in Chinese), 17(1):18-21. |
| [17] | R H T, Goloshubin G, Hilterman F J. 2009. Poroelastic analysis of amplitude-versus-frequency variations[J]. Geophysics, 74(6):N41-N48. |
| [18] | Su Q, Li H L, Lv B, et al. 2011. 3D Prestack seismic imaging in Baka area of northern Turpan-hami basin[J]. China Petroleum Exploration (in Chinese), (5-6):29-40. |
| [19] | Wang B Z, Zhu Y, Wang D. 2008. Fluid mechanism models and their velocity dispersions in porous media[J]. Progress in Exploration Geophysics (in Chinese), 31(6):405-413. |
| [20] | Wang D X, Xin K F, Li Y M, et al. 2006. An experimental study of influence of water saturation on velocity and attenuation in sandstone under stratum conditions[J]. Chinese Journal of Geophysics (in Chinese), 49(3):908-914. |
| [21] | White J E. 1975. Computed seismic speeds and attenuation in rocks with partial gas saturation[J]. Geophysics, 40(2):224-232. |
| [22] | Zhang K. 2012. From tight oil & gas to shale oil & gas-approach for the development of unconventional oil & gas in China[J]. Chinese Geological Education (in Chinese), (2):11-15. |
| [23] | Zhang Y G. 2014. The full-wave field simulation in saturated porous media using the reflectivity method. Progress in Geophysics (in Chinese), 29(3):1369-1376, doi:10.6038/pg20140351. |
| [24] | Zhao H B, Wang X M, Chen S M, et al. 2010. Acoustic response characteristics of unsaturated porous media[J]. Science China Physics, Mechanics and Astronomy, 53(8):1388-1396. |
| [25] | Zhao W J, Yang W Y. 2014. Progress of frequency-dependent AVO hydrocarbon detection technology[J]. Progress in Geophysics (in Chinese), 29(6):2858-2865, doi:10.6038/pg20140656. |
| [26] | 李胜军,孙成禹,高建虎,等. 2008.地震波数值模拟中的频散压制方法分析.石油物探, 47(5):444-448. |
| [27] | 李胜军,高建虎,雍学善,等. 2012.球面波的反射P波AVO分析[J].地球物理学报, 50(10):3459-3466, doi:10.6038/j.issn.0001-5733.2012.10.029. |
| [28] | 李胜军,高建虎,张军舵,等. 2013.体纹理属性提取技术研究及应用[J].地球物理学进展, 28(3):1563-1569, doi:10.6038/pg20130353. |
| [29] | 刘兰锋,曹思远,李绪宣,等. 2010.未固结含气砂岩储层低频地震响应特征研究[J].石油地球物理勘探, 45(6):873-878. |
| [30] | 任青春,文一华,郑雷清,等. 2012.叠前反演的致密砂岩储层预测和含油气性检测[J].吐哈油气, 17(1):18-21. |
| [31] | 苏勤,李海亮,吕彬,等. 2011.吐哈盆地北部山前带巴喀三维叠前地震成像处理解释技术研究及应用[J].中国石油勘探, (5-6):29-40. |
| [32] | 王炳章,朱晔,王丹. 2008.多孔介质的流体机制模型及其频散机理[J].勘探地球物理进展, 31(6):405-413. |
| [33] | 王大兴,辛可锋,李幼铭,等. 2006.地层条件下砂岩含水饱和度对波速及衰减影响的实验研究[J].地球物理学报, 49(3):908-914. |
| [34] | 张抗. 2012.从致密油气到页岩油气——中国非常规油气发展之路探析[J].中国地质教育, (2):11-15. |
| [35] | 张莹革. 2014.饱和流体多孔隙介质反射率法全波场模拟[J].地球物理学进展, 29(3):1369-1376, doi:10.6038/pg20140351. |
| [36] | 赵海波,王秀明,陈树民,等. 2010.未饱和孔隙介质的声场响应[J].中国科学:物理学力学天文学, 40(7):817-827. |
| [37] | 赵万金,杨午阳. 2014.频变AVO油气检测技术进展[J].地球物理学进展, 29(6):2858-2865, doi:10.6038/pg20140656. |
 2015, Vol. 30
2015, Vol. 30

