2. 资源与环境信息系统国家重点实验室, 中科院地理科学与资源研究所, 北京 100101;
3. 中国地质大学(北京)地球物理与信息技术学院, 北京 100083
2. State Key Laboratory of Resources and Environmental Information System, Institute of Geographic Science and Natural Resources Research, CAS, Chaoyang District, Beijing 100101, China;
3. School of Geophysics and Information Technology, China University of Geosciences, Beijing 100083, China
远震P波记录中包含了大量地震台站下方地壳和上地幔速度间断面所产生的PS转换波及其多次反射波的信息,由此提取的接收函数是了解地壳上地幔速度精细结构的重要手段.早期接收函数主要应用在一维速度结构研究(Burdick and Langston,1977;Langston,1977,1979),也可以用来追踪速度间断面(Kosarev et al.,1999).随着全球数字地震台站数量的增加和观测技术的完善,接收函数研究趋势向高分辨率成像方向发展.借鉴地震勘探中成熟的处理技术(Yilmaz,1987),利用数字信号分析和波传播理论,得到2D或3D的地下精细结构(王伟等,2011;沈旭章,2013; 张攀等,2014).随着宽频带地震台站密度的增加和新技术的引进,接收函数方法在正反演和偏移两个方向上有长足的发展,并且对地下结构及物性参数的研究更加精细.接收函数已经成为研究地壳上地幔速度结构的一种非常重要的方法手段(吴庆举和曾融生,1998;段永红等,2005;徐强等,2009;王晨阳和黄金莉,2012;叶卓等,2013),同时也可以和其他地球物理方法联合使用来研究壳幔速度结构(胡家富等,2005;彭淼等,2012).
将地震勘探处理技术中的波动方程偏移成像方法引入到接收函数阵列,按照偏移成像的概念,要将观测数据的转换震相按照地震波传播的反方向聚集到转换点上.Ryberg和Weber(2000)提出了接收函数转换波与地震勘探中的反射波的等效时距关系,提出将反射地震勘探方法应用到接收函数阵列上.吴庆举等(2007)提出了一种接收函数的克希霍夫偏移成像方法,这种方法能够适应介质速度的横向变化,提高接收函数成像的精度和分辨率,实现转换波的有效归位.在此基础上,田小波等(2004)引入了隐式差分多重网格算法提高了有限差分的精度、稳定性和计算效率,在数值模拟过程中提出了延迟边界条件,有效地消除了正演过程中的边界效应.王红落等(2005)利用波动方程有限差分的算法实现了接收函数的正演和偏移,实现了对点绕射和穹隆构造模型的高精度成像.
本文考虑地震波动力学特征,利用波动方程有限差分的算法数值模拟接收函数.根据马德堂和朱光明(2003)的波场分离理论,将接收函数分离成P波接收函数从和S波接收函数进行正演模拟.得到理论的接收函数波形记录后,引入反射地震勘探中的逆时偏移方法,实现了接收函数阵列的偏移成像.数值结果表明,成像具有很高的精度.
1 基于波场分离的接收函数正演地震台站所记录到的三分量远震P波地震记录(Langston,1979)可以表示为

其中,D V(t)、 D R(t)和D T(t)分别表示地震记录的垂直分量、径向分量和切向分量, E V(t)、 E R(t)和E T(t)分别表示接收介质脉冲响应的垂直、径向和切向分量,S(t)表示平面入射的远震P波波形的等效震源函数, I(t)表示仪器的脉冲响应.接收函数是由 D R(t)、 D T(t)分别和D V(t)反褶积得到的.因此,要正演接收函数,先要正演三分量地震记录.本文主要研究二维情况,即两分量的地震记录正演计算.
利用马德堂的纵横波场分离理论,将普通的二阶弹性波速度-应力方程通过引入新变量 S p和S s改造成纵、横波分离的弹性波方程,总波场 S 可以表示为全纵波和全横波之和,即 S = S p+ S s.本文采用张建磊提出的二维纵、横波分离模拟方程,具体形式如下(Virieux,1984,1986;张建磊等,2008):


式中,λ和μ为拉梅系数,t是时间,(τxx,τzz,τxz)表示应力张量,(u,w)表示质点在x和z方向上的速度,Vp和Vs分别表示纵、横波的速度.
本文采用交错网格有限差分的数值模拟方法.震源采用平面P波从模型底部入射,边界条件选用完美匹配层边界条件(Berenger,1994),差分格式采用时间二阶、空间十阶.
2 波动方程叠前逆时偏移常用的叠前偏移方法主要有单程波动方程偏移和克希霍夫偏移两种,但是这两种方法都不能对复杂介质实现精确成像,而逆时偏移是采用全波动方程方法,没有对上行波和下行波进行分离,而直接利用全波信息进行成像,能够较好地处理横向的不均匀性,是目前已知偏移方法中比较精确的一种(李文杰等,2008;周学明等,2013;吴国忱和秦海旭,2014).
叠前逆时偏移主要分两步来完成:延拓和成像.
延拓包括两个部分,一是震源波场的正向延拓,计算有震源激发得到的地震波场,也就是上述的正演过程,得到整个时间轴上的波场信息和地震台站接收到的“单炮记录”;二是检波点波场的逆时延拓,对“单炮记录”的数据沿着时间轴进行反向延拓.
叠前逆时偏移的第二步是成像,每逆时延拓一个波场,就将正演得到的震源波场和逆时外推的检波点波场利用成像条件做成像运算,然后对整个时间轴的成像值沿时间方向叠加,得到最终成像结果.本文采用的是互相关成像条件.
在得到成像结果后,成像剖面中会存在假象,多为低频干扰.这是由于在延拓过程中遇到分界面时产生的反射波在应用成像条件时会被当作成像值加入成像剖面中,从而产生假象.本文采用Laplace滤波的方法来压制低频噪声.
具体的计算流程如图 1所示:
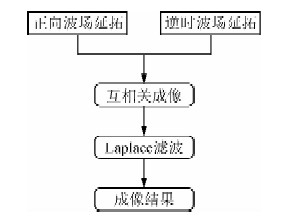 | 图 1 逆时偏移流程图 Fig. 1 Flow chart of time-reverse migration |
首先通过弹性波场的数值模拟来验证波场分离方法的正确性,建立速度模型如图 2a所示,分界面上下横波速度分别为3.6 km/s和4.0 km/s.给出模型的S波速度,由公式Vp= 和ρ=0.32Vp+0.77可以得到P波速度和密度,进而得到拉梅系数.经过数值计算,得到的两分量波场分离的地震图如图 2b-d所示,从正演结果可以验证基于波场分离的有限差分的地震模拟方法的有效性.
和ρ=0.32Vp+0.77可以得到P波速度和密度,进而得到拉梅系数.经过数值计算,得到的两分量波场分离的地震图如图 2b-d所示,从正演结果可以验证基于波场分离的有限差分的地震模拟方法的有效性.
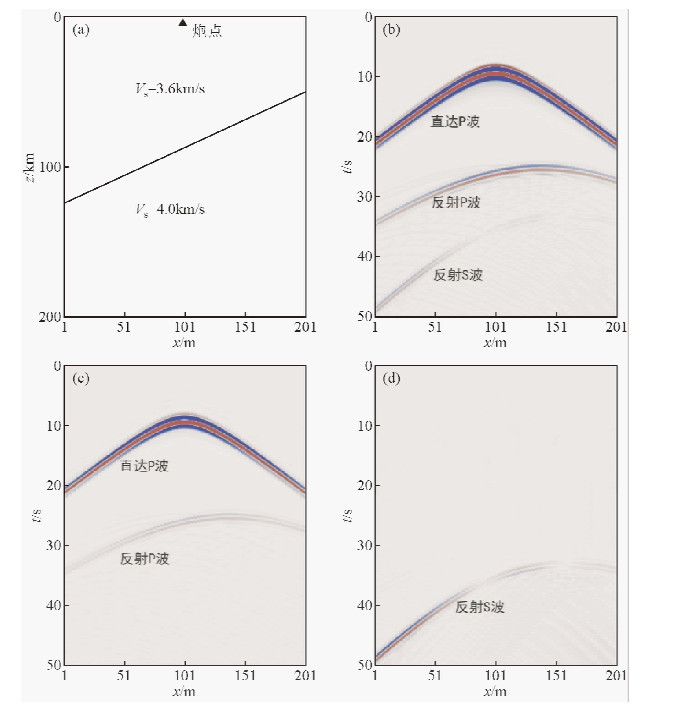 | 图 2 弹性波场正演模型与地震记录的Z分量 (a)为上倾界面地质模型,(b)、(c)、(d)分别为正演的总波场、纯P波波场和纯S波波场的Z分量. Fig. 2 Model of the elastic wave field forward modeling and Z component of the seismic record (a) The model of updip interface, (b)、(c)、(d) the Z component of the full wave field、P-wave field and S-wave field. |
对散射点模型进行接收函数的正演,模型参数如图 3a所示,整个区域除了在模型中心有一个3.2 km/s的散射点外,其余部分横波速度为4.0 km/s.数值模拟的结果表明波场分离的波动方程正演接收函数阵列的可行性.
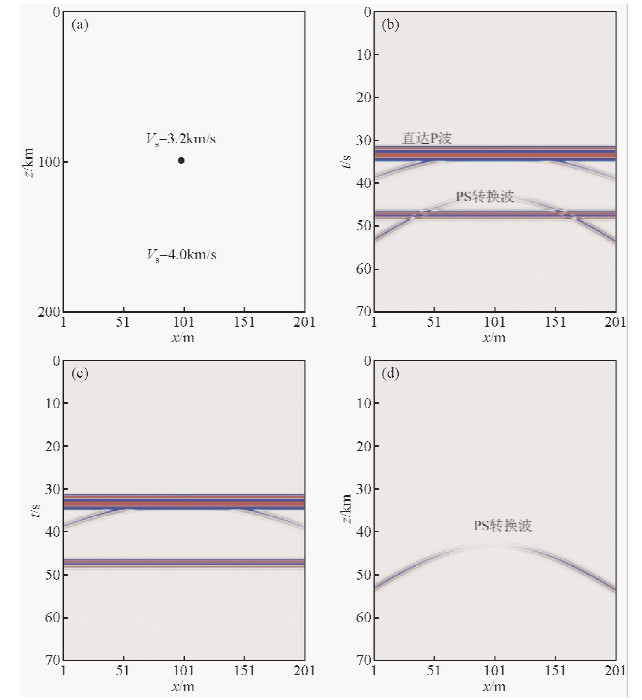 | 图 3 散射点模型与地震记录的Z分量 (a) 散射点模型,(b)、(c)、(d)分别为正演的总波场、纯P波波场和纯S波波场的Z分量. Fig. 3 Model of scatter point and Z component of the seismic record (a) The model of scatter point, (b)、(c)、(d) the Z component of the full wave field、P-wave field and S-wave field. |
选择相对简单的模型,利用上述的正演方法,数值模拟两分量的地震记录,然后利用叠前逆时偏移的方法对得到的PS转换波的地震记录进行偏移成像工作,得到最终的偏移剖面.模型的横波速度见表 1,纵波速度和拉梅系数依经验公式获取,具体模型及偏移结果如图 4所示.
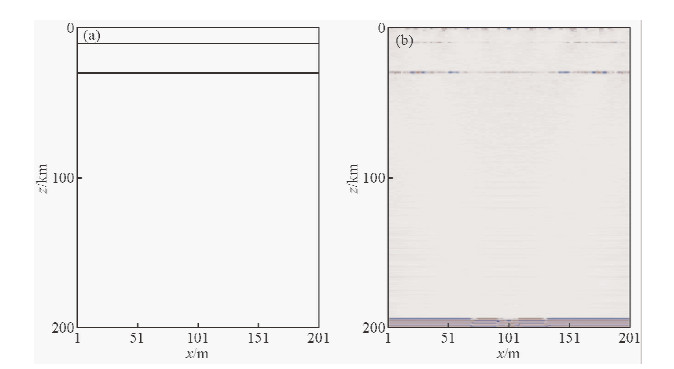 | 图 4 地表低速层模型及成像 (a)地震模型; (b)成像结果. Fig. 4 Model of lower velocity layers at the surface and the imaging (a) Seismic Model; (b) Imaging result. |
再选取一个相对复杂的地震模型如图 5a,横波速度如表 1所示,正演其波场并进行叠前逆时偏移后得到的成像结果如图 5b所示.从二者的结果对比来看,叠前逆时偏移能够对较复杂的地震模型进行更精确的高精度成像.
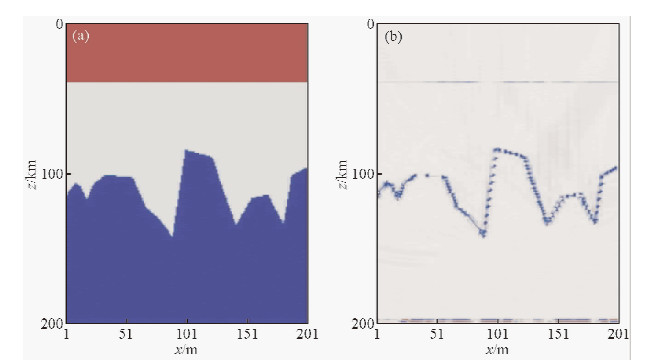 | 图 5 复杂模型及成像 (a)地震模型; (b)成像结果. Fig. 5 Complex model and the imaging (a) Seismic model; (b) Imaging result. |
|
|
表 1 接收函数偏移模型参数 Table 1 Model parameters of receiver function migration |
在叠前逆时偏移过程中需要选取震源波场作为正演波场,可供选择的有总波场、全P波波场和全S波波场三种.分别对这三种波场进行偏移成像,速度模型如图 6a所示,凹曲间断面上下横波速度分别为3.6 km/s和4.5 km/s,纵波速度和拉梅系数依经验公式获取,偏移得到的结果如图 6所示.从图中可以看到,总波场和全P波波场作为正演波场进行的偏移成像结果虽然能大致描绘模型的形态,但是在模型上半部分存在明显的噪声,而全S波波场的成像结果就基本不存在这个问题.分析原因,S波是只在速度间断面处才开始产生,所以不含间断面以下区域的地震信息,而P波波场含有整个模型空间的信息,所以S波波场与P波波场相比,能更好地反映模型内部速度间断面的信息.
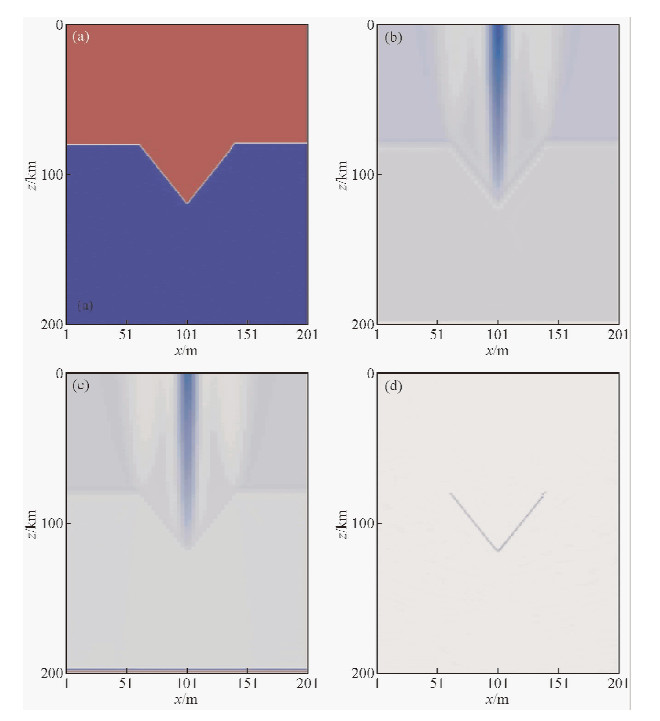 | 图 6 不同正演波场对偏移结果的影响 (a) 为地震模型,(b)、(c)、(d)分别为总波场、全P波波场和全S波波场的偏移结果. Fig. 6 The effects of forward modeling wave fields on the migration result (a) Seismic mode, (b)、(c)、(d) shows the imgration result of the whole wavefiled, P-wave field and S-wave field respectively. |
本文通过波场分离的理论将接收函数阵列分离成P波和S波的单独阵列,并引入勘探地震处理技术中常用的叠前逆时偏移成像对其进行偏移成像.通过数值实验得到的结果表明,基于波场分离的有限差分数值模拟方法能够较好的正演接收函数阵列,而叠前逆时偏移成像技术可以较好地对简单构造进行高精度成像.通过对比纯P波阵列、纯S波阵列和全波场阵列的成像结果发现,利用接收函数的纯S波阵列进行叠前逆时偏移能够获得较高精度的成像结果.
致 谢 本文得到国家自然基金项目(41130419、41240027、41374061)和博士后基金(2012M510533)支持,特此致谢.感谢审稿专家和编辑部的支持.
| [1] | Berenger J P. 1994. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 114(2):185-200. |
| [2] | Burdick L J, Langston C A. 1977. Modeling crustal structure through the use of converted phases in teleseismic body waves[J]. Bull. Seismol. Soc. Am., 67(3):677-691. |
| [3] | Duan Y H, Zhang X K, Liu Z, et al. 2005. A study on crustal structures of Changbaishan-Jingpohu volcanic area using receiver functions[J]. Chinese J. Geophys. (in Chinese), 48(2):352-358, doi:10.3321/j.issn:0001-5733.2005.02.017. |
| [4] | Hu J F, Zhu X G, Xia J Y, et al. 2005. Using surface wave and receiver function to jointly inverse the crust-mantle velocity structure in the West Yunnan area[J]. Chinese J. Geophys. (in Chinese), 48(5):1069-1076, doi:10.3321/j.issn:0001-5733.2005.05.013. |
| [5] | Kosarev G, Kind R, Sobolev S V, et al. 1999. Seismic evidence for a detached Indian lithospheric mantle beneath Tibet[J]. Science, 283(5406):1306-1309. |
| [6] | Langston C A. 1977. Corvallis, Oregon, crustal and upper mantle receiver structure from teleseismic P and S waves[J]. Bull. Seismol. Soc. Am., 67(3):713-724. |
| [7] | Langston C A. 1979. Structure under Mount Rainier, Washington, inferred from teleseismic body waves[J]. J. Geophys. Res., 84(B9):4749-4762. |
| [8] | Li W J, Wei X C, Ning J R, et al. 2008. The discussion of reverse time depth migration and wavefield separation for pre-stack elastic data[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 30(6):447-456. |
| [9] | Ma D T, Zhu G M. 2003. Numerical modeling of P-wave and S-wave separation in elastic wavefield[J]. Oil Geophysical Prospecting (in Chinese), 38(5):482-486. |
| [10] | Peng M, Tan H D, Jiang M, et al. 2012. Joint inversion of receiver functions and magnetotelluric data:Application to crustal and mantle structure beneath central Namche Barwa, eastern Himalayan syntaxis[J]. Chinese J. Geophys. (in Chinese), 55(7):2281-2291, doi:10.6038/j.issn.0001-5733.2012.07.014. |
| [11] | Ryberg T, Weber M. 2000. Receiver function arrays:a reflection seismic approach[J]. Geophysical Journal International, 141(1):1-11. |
| [12] | Shen X Z. 2013. Imaging structures of crust and upper mantle beneath the source of the 14 April 2010 Yushu, Qinghai earthquake using P-and S-wave receiver functions[J]. Chinese J. Geophys. (in Chinese), 56(2):495-503, doi:10.6038/cjg20130213. |
| [13] | Tian X B, Wu Q J, Zeng R S. 2004a. Multi-grid algorithm for numerical modeling of elastic wave field using finite-difference method[J]. Chinese J. Geophys. (in Chinese), 47(1):81-87, doi:10.3321/j.issn:0001-5733.2004.01.012. |
| [14] | Tian X B, Wu Q J, Zeng R S. 2004b. Delay boundary conditions for elastic wave modeling[J]. Chinese J. Geophys. (in Chinese), 47(2):268-273, doi:10.3321/j.issn:0001-5733.2004.02.013. |
| [15] | Virieux J. 1984. SH-wave propagation in heterogeneous media:Velocity-stress finite-difference method[J]. Geophysics, 49(11):1933-1942. |
| [16] | Virieux J. 1986. P-SV wave propagation in heterogeneous media:Velocity-stress finite-difference method[J]. Geophysics, 51(4):889-901. |
| [17] | Wang C Y, Huang J L. 2012. Mantle transition zone structure around Hainan by receiver function analysis[J]. Chinese J. Geophys. (in Chinese), 55(4):1161-1167, doi:10.6038/j.issn.0001-5733.2012.04.012. |
| [18] | Wang H L, Chang X, Chen C R. 2005. Receiver function forward modeling and migration based on wave-equation finite difference method[J]. Chinese J. Geophys. (in Chinese), 48(2):415-422, doi:10.3321/j.issn:0001-5733.2005.02.026. |
| [19] | Wang W, Gao X, Li Y Y, et al. 2011. Crustal velocity structure of S-wave beneath Tibetan Plateau with transform function method——Hi-CLIMB Profile[J]. Chinese J. Geophys. (in Chinese), 54(11):2769-2778, doi:10.3969/j.issn.0001-5733.2011.11.007. |
| [20] | Wu G C, Qin H X. 2014. Elastic reverse time migration in isotropic medium based on random boundary[J]. Progress in Geophysics (in Chinese), 29(4):1815-1821, doi:10.6038/pg20140444. |
| [21] | Wu Q J, Zeng R S. 1998. The crustal structure of Qinghai-Xizang plateau inferred from broadband teleseismic waveform[J]. Acta Geophysica Sinica (in Chinese), 41(5):669-679. |
| [22] | Wu Q J, Li Y H, Zhang R Q, et al. 2007. 2D Kirchhoff migration for receiver function[J]. Chinese J. Geophys. (in Chinese), 50(2):539-545, doi:10.3321/j.issn:0001-5733.2007.02.027. |
| [23] | Xu Q, Zhao J M, Cui Z X, et al. 2009. Structure of the crust and upper mantle beneath the southeastern Tibetan Plateau by P and S receiver function[J]. Chinese J. Geophys. (in Chinese), 52(12):3001-3008, doi:10.3969/j.issn.0001-5733.2009.12.009. |
| [24] | Ye Z, Li Q S, Gao R, et al. 2013. Seismic receiver functions revealing crust and upper mantle structure beneath the continental margin of southeastern China[J]. Chinese J. Geophys. (in Chinese), 56(9):2947-2958, doi:10.6038/cjg20130909. |
| [25] | Yilmaz O. 1987. Seismic Data Processing[M]. Tulsa:Society of Exploration Geophysics. |
| [26] | Zhang J L, Tian Z P, Wang C X. 2008. Elastic wave simulation of P-and S-waves separation by 2-D staggered grid and application[J]. Oil Geophysical Prospecting (in Chinese), 43(6):717-722. |
| [27] | Zhang P, Zhu L B, Chen H P, et al. 2004. Crustal structure in China from teleseismic receiver function[J]. Acta Seismologica Sinica (in Chinese), 36(5):850-861. |
| [28] | Zhou X M, Li Q C, Ma T. 2013. Prestack reverse time migration for elastic wave[J]. Geophysical and Geochemical Exploration (in Chinese), 37(2):274-279. |
| [29] | 段永红,张先康,刘志,等. 2005.长白山-镜泊湖火山区地壳结构接收函数研究[J].地球物理学报, 48(2):352-358, doi:10.3321/j.issn:0001-5733.2005.02.017. |
| [30] | 胡家富,朱雄关,夏静瑜,等. 2005.利用面波和接收函数联合反演滇西地区壳幔速度结构[J].地球物理学报, 48(5):1069-1076, doi:10.3321/j.issn:0001-5733.2005.05.013. |
| [31] | 李文杰,魏修成,宁俊瑞,等. 2008.叠前弹性波逆时深度偏移及波场分离技术探讨[J].物探化探计算技术, 30(6):447-456. |
| [32] | 马德堂,朱光明. 2003.弹性波波场P波和S波分解的数值模拟[J].石油地球物理勘探, 38(5):482-486. |
| [33] | 彭淼,谭捍东,姜枚,等. 2012.利用接收函数和大地电磁数据联合反演南迦巴瓦构造结中部地区壳幔结构[J].地球物理学报, 55(7):2281-2291, doi:10.6038/j.issn.0001-5733.2012.07.014. |
| [34] | 沈旭章. 2013. 2010年玉树7.1级地震震源区P和S波接收函数成像[J].地球物理学报, 56(2):495-503, doi:10.6038/cjg20130213. |
| [35] | 田小波,吴庆举,曾融生. 2004a.弹性波场数值模拟的隐士差分多重网格算法[J].地球物理学报, 47(1):81-87, doi:10.3321/j.issn:0001-5733.2004.01.012. |
| [36] | 田小波,吴庆举,曾融生. 2004b.弹性波场数值模拟的延迟边界方法[J].地球物理学报, 47(2):268-273, doi:10.3321/j.issn:0001-5733.2004.02.013. |
| [37] | 王晨阳,黄金莉. 2012.应用接收函数方法研究海南及其邻区地幔转换带结构[J].地球物理学报, 55(4):1161-1167, doi:10.6038/j.issn.0001-5733.2012.04.012. |
| [38] | 王红落,常旭,陈传仁. 2005.基于波动方程有限差分算法的接收函数正演与偏移[J].地球物理学报, 48(2):415-422, doi:10.3321/j.issn:0001-5733.2005.02.026. |
| [39] | 王伟,高星,历玉英,等. 2011.用转换函数研究青藏高原地壳S波速度结构——"Hi-CLIMB"剖面[J].地球物理学报, 54(11):2769-2778, doi:10.3969/j.issn.0001-5733.2011.11.007. |
| [40] | 吴国忱,秦海旭. 2014.各向同性弹性波随机边界逆时偏移[J].地球物理学进展, 29(4):1815-1821, doi:10.6038/pg20140444. |
| [41] | 吴庆举,曾融生. 1998.用宽频带远震接收函数研究青藏高原的地壳结构[J].地球物理学报, 41(5):669-679. |
| [42] | 吴庆举,李永华,张瑞青,等. 2007.接收函数的克希霍夫2D偏移方法[J].地球物理学报, 50(2):539-545, doi:10.3321/j.issn:0001-5733.2007.02.027. |
| [43] | 徐强,赵俊猛,崔仲雄,等. 2009.利用接收函数研究青藏高原东南缘的地壳上地幔结构[J].地球物理学报, 52(12):3001-3008, doi:10.3969/j.issn.0001-5733.2009.12.009. |
| [44] | 叶卓,李秋生,高锐,等. 2013.中国大陆东南缘地震接收函数与地壳和上地幔结构[J].地球物理学报, 56(9):2947-2958, doi:10.6038/cjg20130909. |
| [45] | 张建磊,田振平,王成祥. 2008.二维交错网格纵横波分离的弹性波模拟及应用[J].石油地球物理勘探, 43(6):717-722. |
| [46] | 张攀,朱良保,陈浩朋,等. 2014.用接收函数方法研究中国境内地壳结构[J].地震学报, 36(5):850-861. |
| [47] | 周学明,李庆春,马婷. 2013.弹性波叠前逆时偏移[J].物探与化探, 37(2):274-279. |
 2015, Vol. 30
2015, Vol. 30


