2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 青岛 266061
2. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, 266061, China
近20年来,计算机数据处理与运算能力不断增强,GPS测量、卫星测高、卫星重力测量等空间测绘技术迅速发展,国际地球参考框架(ITRF)逐年精化,成为全球和区域参考框架的基准(陈俊勇,2005,2007;刘经南等,2013),这一切为提高重力数据精确度与准确度,促进重力数据的一致性与相容性,扩大重力数据应用领域和用途范围奠定了基础.同时,现代的大地测量、固体地球物理、海洋、冰川、水资源等研究领域又迫切需要高精度和全频段的地球重力场数据,由此推动了北美重力数据归算标准的修订(Hinze et al.,2005).北美重力数据归算新标准(以下简称北美标准)的最大特点在于采用国际公认的地球椭球面,而不是常规使用的各国大地水准面作为重力测点高程基准,其次改进了传统的重力校正方法,提高了重力异常计算精度(曾华霖,2008).遵循修订后标准,北美重力数据库以及加拿大、墨西哥和美国的国家重力数据库数据进行了重新改算.随后,澳大利亚也修订标准完成了国家重力数据库数据的重新改算(Tracey et al.,2007).
我国陆地最新的区域重力调查行业标准为2006年国土资源部发布的DZ/T 0082-2006,即“区域重力调查规范”(中华人民共和国国土资源部,2006),其中对重力异常计算作了“五统一”规定,即统一采用2000国家重力基本网系统;统一采用1954年北京坐标系和1985国家高程基准;统一采用国际大地测量学会(IAG)推荐的1980年公式计算正常重力值;统一采用规范规定的公式进行布格校正和中间层校正,密度统一采用2.67 g/cm3;统一采用166.7 km的半径进行地形校正.其中的中间层密度、地形校正半径参数与北美标准一致.
我国海洋区域重力调查没有专门的行业标准,海洋重力校正一直执行1992年发布、2007年修订的国家标准GB/T 12763.8-2007,即“海洋地质地球物理调查规范”中第9.4.2条“海洋重力测量资料计算与校正”的相关规定(中国国家标准化管理委员会,2007).国土资源部于2009年发布了1:1000000海洋区域地质调查行业标准DZ/T 0247-2009(中华人民共和国国土资源部,2009);中国地质调查局于2012年推出了海域石油和天然气地球物理调查规范DD2012-02和1:250000海洋区域地质调查规范DD2012-03等地调局系统技术标准,其中DD2012-03于2014年升级为海洋区域地质调查行业标准DZ/T 0256-2014(中华人民共和国国土资源部,2014).1:1000000和1:250000海洋区域地质调查行业标准中的重力调查相关条文均等同采用国家标准GB/T 12763.8-2007,其中布格校正采用无限延伸平板的中间层模型,标准未涉及地形校正内容.而DD2012-02技术标准则是针对大陆架地区海域石油和天然气调查制订,其中提出了“准完全布格校正”概念,规定地形校正半径为40 km.
从本世纪初至2014年,我国海域已完成1:100万区域地质调查的全海域覆盖.随着海洋区域重力调查和研究的深入,业内对如何实施更完善的布格校正(高德章,2006;吕川川等,2009;高金耀等,2014;尹文笋和张建中,2014)、如何与陆地接轨实施重力异常数据的海陆联编、如何与国际接轨实现重力资料的洲际或大区域应用等问题多有讨论,并在实际工作中作了新的尝试(温珍河等,2014;杨金玉等,2014),但迄今还没有更新的规范出台.
参考北美及澳大利亚新标准中采用的重力校正计算方法,对比区域重力调查规范 DZ/T 0082-2006(以下简称陆地标准)中的陆地重力校正方法,本文对常规重力校正的传统近似方法及精确计算公式作了回顾总结,并针对海洋地质地球物理调查规范GB/T 12763.8-2007 第9.4.2条“海洋重力测量资料计算与校正”(以下简称海洋标准)中规定的海洋实测重力数据的重力校正有关条文,提出了相应修改建议.以尽最大可能保证重力校正在消除各类非地质因素过程中的客观化、定量化及全面化,使重力校正过程获取的重力异常确定无疑义,不确定因素移交地质解释过程中处理(LaFehr,199la).从而增强不同源重力数据集之间的互融性,提高重力异常的数据质量,扩大重力数据的应用范围.
1 重力校正与基准面出于水准测量目的,传统大地测量学利用重力来测定大地水准面形状,地球物理学将相关技术引入地质勘探领域,利用重力探测地球内部的横向密度变化,实现地质勘探目的.勘探地球物理所谓的重力校正(重力归算)是将观测点的原始重力观测值转换成重力异常形式的过程.假设地球是一质量均匀或呈同心层状均匀分布的旋转椭球体,各项重力校正就是从实测重力值中逐步消除该标准地球模型,即地球椭球体的重力效应,最后获得由测点所在地表面偏离地球椭球面(传统以大地水准面近似替代)的高差、以及偏离地球椭球正常质量分布的密度异常体所引起的重力异常(王宝仁,1986).
除重力仪零点漂移校正、以及海洋、航空重力测量过程中的厄特渥斯校正外,常规重力校正包括:
(1)正常重力值校正,也称纬度校正,选择与大地水准面最佳逼近的地球椭球体作为参考椭球(见图 1),正常重力校正值为参考椭球面上测点所在纬度的理论重力值.
 | 图1 大地水准面,椭球面和地表面示意图 Fig.1 Geoid, ellipsoid and topographic surface |
(2)高度校正,高度校正是陆地标准与北美标准的称谓,海洋标准称空间校正.空间或自由空间或自由空气校正术语源自传统大地测量学(Li and Götze,2001),意为将测点归算到大地水准面上,即测点与基准面之间物质除空气之外全部压缩至大地水准面,让大地水准面成为地球质量的包络面,由此依据斯托克斯定理利用重力计算大地水准面起伏高度;而勘探地球物理以地球内部密度异常体为目标,很难接受改变重力测点与异常体之间空间位置的理论,因此对地球物理而言称高度校正比较合理.高度校正值为测点相对参考椭球面高度的重力效应,高度校正用于消除因测点不在参考椭球面上,即高于或低于参考椭球面导致的正常重力值变化.
(3)布格校正,这里指陆地标准所谓的中间层校正,海洋标准按欧美习惯,将中间层校正称作布格校正;陆地标准按前苏联习惯,将高度校正与中间层校正合称布格校正.假设参考椭球面与测点之间的岩层(中间层)是一无限延伸的平板或考虑地球曲率影响时的球冠,布格校正目的就是消除按正常密度分布的该中间层物质的重力效应.
(4)地形校正,属陆地的常规校正项,海洋标准中未列地形校正要求.地形校正是布格校正的进一步完善,地形校正值为相对布格校正平板或球冠顶、底面的地形起伏或海底水深变化的重力效应,地形校正实际上是将平板或球冠外部的物质削去、内部空缺填满的过程.国际上将未经地形校正的布格校正称作简单布格校正,而经过地形校正的布格校正称完全布格校正(Chapin,1996).
理论上重力校正的基准面应该是参考椭球面,但在GPS(美国全球卫星定位系统)出现之前,测点相对参考椭球面的大地高(椭球高h,见图 2)难以获取,只有相对大地水准面的高程(H)能被准确测量,因此传统上以大地水准面近似替代参考椭球面作为重力校正的垂向基准面.随着GPS直接测量大地高成为可能,采用参考椭球面作为重力校正基准面已无任何技术障碍,只是改变传统习惯的必要性问题值得讨论.
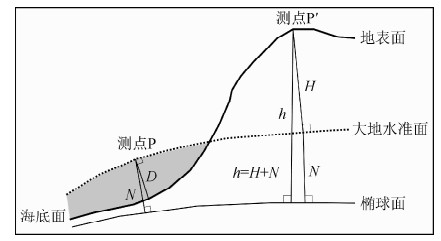 |
图 2 高程H、大地水准面高N、
大地高 |
大地水准面相对参考椭球面起伏(N)的重力效应称地球物理间接效应,间接效应属长波长的低频扰动,就局部地区的地质勘探目的,其影响完全可以忽略(Li and Götze,2001),但对洲际或大区域应用拟考虑其影响(Hinze et al.,2005).
北美与澳大利亚的重力校正基准面均采用国际大地测量和地球物理学联合会(IUGG)推荐的参考椭球GRS80(Hinze et al.,2005;Tracey et al.,2007),随着GPS定位系统的全面应用,我国地球物理界对重力校正采用国家高程基准的问题也早有讨论(励宝恒,1996).将来我国的重力校正基准面,是选择GRS80,还是2008年7月启用的2000国家大地坐标系参考椭球CGCS2000(国家测绘局,2008),这是需要待定的问题.
2 正常重力公式旋转椭球面上正常重力值的精确计算公式由Somigliana闭合式给出(Hinze et al.,2005):

为了便于计算,传统上采用公式(2)的近似表达式,即公式(1)的二阶级数展开式计算正常重力值(Li and Götze,2001):
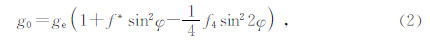
式中: g0为参考椭球面上地理纬度φ处的正常重力值; k= 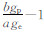 -1,ge赤道重力值,gp极地重力值;e=
-1,ge赤道重力值,gp极地重力值;e= 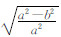 参考椭球第一偏心率,a、b参考椭球长、短半轴;f*=
参考椭球第一偏心率,a、b参考椭球长、短半轴;f*=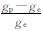 参考椭球重力扁率;
参考椭球重力扁率;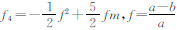 参考椭球扁率,
参考椭球扁率,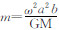 ,ω地球自转角速度,GM地心引力常数.
,ω地球自转角速度,GM地心引力常数.
将不同的参考椭球参数代入公式(1)或(2)即得到不同的正常重力公式.北美标准采用基于GRS80椭球的公式(1)执行正常重力值的精确计算;陆地标准采用基于GRS80椭球的公式(2),即公式(3)作为正常重力公式.公式(3)也是1980年国际正常重力公式,是国际大地测量协会(IAG)推荐的最新国际正常重力公式(Moritz,2000),表达式为
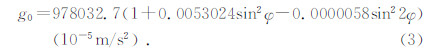
海洋标准采用的正常重力公式见公式(4),标准中称其为1985年国际正常重力公式,其实是将美国国防部制图局1987年公布的WGS84椭球参数代入公式(1)的结果(The Defence of Mapping Agency,1987a,1987b):

公式(4)常在文献中被称为1987年正常重力公式(Reynolds,2011).从1987年至今,WGS84经过四次精化,参考框架从1987年的WGS84演进为1994年的WGS84(G730)、1997年的WGS84(G873)、2002年的WGS84(G1150)、2012年的WGS84(G1674),WGS84椭球参数也随之精化(Wong et al.,2012).因此严格上说,海洋标准中规定的正常重力公式无论是名称还是系数均有必要修订.按公开发表的GRS80、WGS84及CGCS2000最新椭球参数(Moritz,2000;National Imagery and Mapping Agency,1997;魏子卿,2008a),表 1列出了与公式(1)相应的系数,供修订参考.
|
|
表 1 Somigliana闭合式正常重力公式系 Table 1 Constants required to compute normal gravity using Somigliana’s closed formula |
地理纬度φ、大地高h测点相对参考椭球面的正常重力值垂向变化δgh由公式(5)的二阶泰勒级数展开式给出(Hinze et al.,2005):
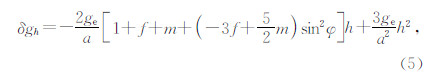
式中:δgh为高度校正值,校正值符号按北美标准设置,测点实测重力值g经正常重力值校正和高度校正后得到空间重力异常ΔgF为
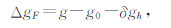
其中,ge赤道重力值; f=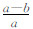 参考椭球扁率,a、b参考椭球长、短半轴;m=
参考椭球扁率,a、b参考椭球长、短半轴;m=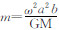 ,ω地球自转角速度,GM地心引力常数;h为相对参考椭球面的大地高.
,ω地球自转角速度,GM地心引力常数;h为相对参考椭球面的大地高.
高度校正计算公式从正常重力公式推导而得,因此两者采用的参考椭球必须一致.将GRS80椭球参数代入公式(5)给出北美标准的高度校正计算公式,见公式(6). WGS84和CGCS2000椭球参数代入公式(5)给出的高度校正计算公式同公式(6),其中h单位m,δgh单位10-5m/s2,表达式为
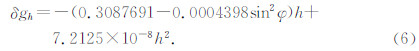
设φ=45°,仅提取公式(6)中的一次项,给出海洋标准的高度校正计算公式,也就是传统采用的将地球近似为球体的高度校正计算公式,即

理论上h=H+N(见图 2),其中H为测点相对大地水准面的高程,N为大地水准面相对参考椭球面的起伏高度,低于参考椭球面N取负值.当海面走航测量时,有
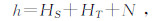
其中HS为重力仪弹性系统至船只吃水线高度,HT为重力观测时从大地水准面(平均海平面)起算的瞬时潮高.
传统上近似用大地水准面替代参考椭球面,即取N≈0,对于海洋重力测量,有h≈HS+HT,仪器高HS相应的高度校正值不大,一般在基点联接、传递绝对重力值时作为常差或分段常差随同仪器零漂校正分配到各测点;而潮高HT一般不会超过10 m,因此公式(7)完全能满足精度要求.
如果采用参考椭球面作为高度校正基准面,考虑全球范围内大地水准面与参考椭球面之间存在最大±100 m的高差(Hinze et al.,2005),公式(6)中的二次项影响在10-4量级,一次项的纬度相关校正项影响在10-2量级,此时,对于区域性的高精度勘测,有必要考虑纬度相关的一次项影响.
4 简单布格校正公式简单布格校正用于消除参考椭球面与测点之间的中间层重力效应,中间层模型有两种,即无限延伸平板模型和考虑地球曲率影响的球冠模型.
4.1 平板模型假设参考椭球面与测点之间的岩层,即中间层,为一无限延伸平板,得到公式(8)的陆地布格校正值计算公式为
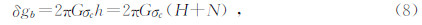
将公式(8)引伸到海域,也就是消除海水层重力效应,同时用正常密度的中间层物质填补,得到海洋布格校正值计算公式为
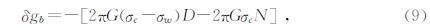
式中:δgb为布格校正值,单位10-5 m/s2,校正值符号按北美标准设置,测点实测重力值g经正常重力值校正、高度校正和布格校正后得到布格重力异常ΔgB为
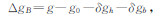
其中,π圆周率Pi;G引力常数,国际科技数据委员会(CODATA)最新推荐值6.67428×10-11 m3/kg/s2(Mohr et al.,2008);σc中间层密度,取2.670×103 kg/m3(Hinze,2003);σw海水密度,海洋标准取1.03×103 kg/m3,北美标准取1.027×103 kg/m3;h陆地中间层厚度,即测点相对参考椭球面大地高,单位m;H测点相对大地水准面高程,H大于零,单位m;D从大地水准面(平均海平面)起算的测点水深(见图 2),D大于零,单位m;N为大地水准面相对参考椭球面起伏高度,低于参考椭球面N取负值,传统取N≈0,单位m.
4.2 球冠模型如果考虑地球曲率影响,无限平板用一球面半径为166.7km的等厚球冠代替,得到更加精确的陆地布格校正值计算公式,也就是北美标准的布格校正值计算公式,见公式(10).与无限平板模型相比,对于2000 m以内的高程变化,166.7 km处截断和地球曲率影响效应在0~1.5(10-5 m/s2)之间波动(LaFehr,1991b),有
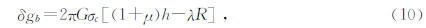
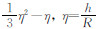 ;
;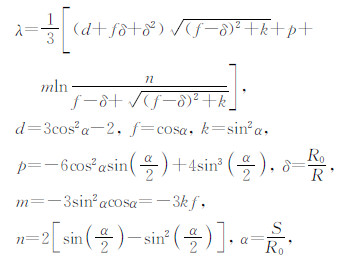
S=166.735 km(LaFehr,1991b).
澳大利亚对公式(10)进行了扩展,使之成为海陆空通用的计算公式(Argast et al.,2009).假设一开角2α、半径S0的圆锥,锥心与地心重合,锥面与球冠顶面重合,测点P距锥面高度为t,见图 3.那么圆锥体在测点P上引起的重力值可表示为S0和t的函数,见公式(11).将公式(11)应用到海域,得到大地水准面上测点P的球冠模型海洋重力布格校正值计算公式,见公式(12).公式(11)为

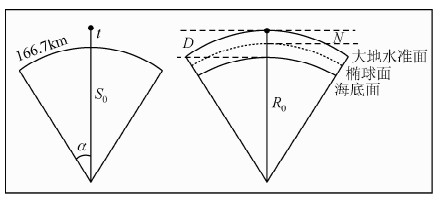 | 图 3 海洋重力布格校正圆锥体与球冠示意图 Fig. 3 The cone and spherical cap for Bouguer correction in the marine case |
其中,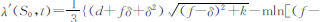
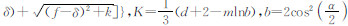 ,
,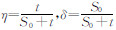 其余参数定义同公式(10).公式(12)为
其余参数定义同公式(10).公式(12)为
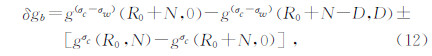
g(σc-σw)(...)表示将参数代入公式(10)计算g(S0,t)时,σ取(σc-σw);gσc(...)表示σ取σc;N大于零时,公式末项的“±”取正号,反之取负号.
5 标准修订建议本文对常规重力校正的传统近似方法及精确计算公式作了回顾总结,在此基础上,就海洋标准的重力校正有关条文提出以下修订建议:
(1)统一重力校正相关术语.海洋标准、陆地标准和北美标准三者的重力校正术语名称及定义各有不同,建议向北美标准靠拢,以便研究成果的国际交流,以及数据的大范围共享.
(2)统一重力校正值符号设置规则.海洋、陆地标准与北美标准的重力校正值符号设置规则不一致,海洋、陆地标准按校正物理意义设置校正值符号,由此带来的符号变化看上去很科学,实际执行异常计算时很容易造成符号混乱.建议一律按“重力观测值=空间异常值+高度校正值+正常重力值”及“重力观测值=布格异常值+布格校正值+高度校正值+正常重力值”规则设置校正值符号.该规则的符号设置结果同北美标准,并能与我国地球物理磁力测量的校正值符号设置方式保持一致,最主要的是易记易用.
(3)保留公式中基础物理常数的常量形式.早期为了简化计算,采用近似公式,并在计算公式中将基础物理常量固化,例如经典的0.0419就是2πG精确到四位小数的固化结果.考虑到基础物理常量在不断精化,建议计算公式中保留基础物理常数的常量形式,在常量说明时给出国际权威机构(例如国际科技数据委员会)推荐的最新常数值.
(4)添加参考椭球面重力垂向基准选项.除大地水准面这一传统基准面外,添加符合国际地球参考框架(ITRF)的参考椭球面作为另一个重力垂向基准选项.该选项将推动纬度、经度平面坐标之外的大地高数据采集,将重力数据从局部二维大地坐标系置于地心三维大地坐标系中;此外选择与ITRF框架相容的坐标系便于必要时的坐标系之间转换.至于选择GRS80、WGS84还是CGCS2000椭球,理论上取决于外业普遍使用的导航定位系统(例如GPS、北斗),即采用外业导航定位的参考椭球系统作为重力观测点水平地理位置及垂向高度基准,实际上三者的坐标值差异很小,甚至可以忽略不计(魏子卿,2008b;程鹏飞等,2009),因此最终涉及的只是名义上的选择.对海洋重力来说,采用参考椭球面作为基准的最大利好是可以直接利用基于ITRF的卫星重力数据,填补勘探程度较低海区的空白(Bacchin et al.,2008),或利用卫星重力数据模拟船载重力数据(Majumdar and Bhattacharyya,2014),实现海洋重力与卫星重力数据的互补或互融.卫星重力数据在海域具有较高的精度和分辨率,随着专用地球重力测量卫星的升空(郑伟等,2010),卫星重力数据精度及分辨率将会有较大提升,未来应用前景广阔.
(5)采用正常重力精确计算公式,并明确所选用的参考椭球体.以目前的计算机编程和计算能力,近似公式与精确公式的计算过程没有区别,那当然采用精确公式执行正常重力值计算.参考椭球体决定了计算公式中的系数值,因此拟明确说明.参考椭球体一旦确定,高度校正公式必须选用同一参考椭球体的椭球参数.
(6)明确定义高度校正公式中的高度变量,如果添加垂向基准,高度校正公式至少应保留纬度相关的一次项.海洋重力测量,高度校正值不大,但作为标准还是应该明确定义高度校正公式中的高度变量,将仪器高、潮高、以及大地水准面高(如果添加垂向基准)以公式方式明确表达.
(7)添加球冠模型布格校正选项.除无限平板模型布格校正公式外,添加球冠模型布格校正公式,供选择使用.
(8)体现海洋布格校正的特殊性.海洋与陆地的布格校正存在物理意义上差异,陆地布格校正中间层物质对测点的引力作用客观存在,而海区布格校正去除海水层、填补中间层,其中的填补物质引力是人为添加的,其对大地水准面以下物质的质量调整无法从物理学理论予以解释.因此Kearey等(1991)认为布格校正适合滨浅海区(一般指水深小于200 m海域),用于消除水深局部变化引起的局部重力效应,追踪地质特征的海域延伸;但不建议深海(一般指水深大于2000 m海域)重力的布格校正,因为人为的布格校正造成巨大的布格正异常,对密度异常体引起的局部重力特征无明显增强作用.美国、加拿大、英国、澳大利亚从上世纪80年代至今出版的全疆域重力异常图均采用陆地布格异常、海区空间异常的联编方案.标准修订后,澳大利亚最新出版的重力异常图依然维持陆地布格异常、海区空间异常的格局(Bacchin et al.,2008).除海域水深数据覆盖率低及精度不高等客观因素外,物理意义差异可能是其中的主要因素.陆地布格异常、海区空间异常符合大地水准面外部无质量存在、内部无质量增减的斯托克斯定理应用条件,能更准确地反映大地水准面的起伏变化.标准中最好能体现海洋布格校正物理意义的特殊性,以便布格校正的合理应用.
(9)纳入地形校正(水深校正)作为非常规重力校正选项.考虑到地形复杂海区的地质勘探需要,有必要在标准中列入相关内容,规范地形校正的方法、技术及精度要求,作为非常规校正项,供需要时选择,让海底地形校正有章可循.
6 结 语随着高精度、全频段地球重力场数据的需求递增,大地测量学界不断呼吁地球物理学界以大地测量方式进行高精度重力校正(Featherstone and Dentith,1997),同时做了大量基础工作,促进大地测量与地球物理学之间的沟通与理解.但对勘探地球物理学界来说,传统的近似计算方法已能满足地质勘探需求,进一步提高精度、改变传统习惯似乎没什么必要.权衡之下,将目光从局部地区的地质勘探,放至区域、洲际乃至全球的区域异常研究,北美各国及澳大利亚最终还是走出传统,采用了新的重力校正计算标准.本文列出了高精度重力校正计算公式,并就海洋标准提出了相应修改建议,以期进一步提高重力异常数据质量,抬升重力数据的信息价值,促进数据大范围共享.
致 谢 感谢审稿专家对本文提出的修改意见,感谢编辑对本文的帮助.
| [1] | Argast D, Bacchin M, Tracey R. 2009. An extension of the closed-form solution for the gravity curvature (Bullard B) correction in the marine and airborne cases[C].//ASEG Extended Abstracts, 2009(1):1-6, doi:10.1071/ASEG2009ab129. |
| [2] | Bacchin M,Milligan P, Wynne P,et al. 2008. Gravity anomaly map of the Australian region (Third Edition), scale 1:5000000. Geoscience Australia, Canberra. |
| [3] | Chapin D A. 1996. The theory of the Bouguer gravity anomaly:a tutorial[J]. The Leading Edge, 15(5):361-363. |
| [4] | Chen J Y. 2005. Contribution and progress in the determination of terrestrial coordinate frame, earth deformation and earth gravity field with spatial geodetic technology-notes on IAG 2005 scientific assembly[J]. Advances in Earth Science (in Chinese), 20(10):1053-1058. |
| [5] | Chen J Y. 2007. Progress in theory and practice for geodetic reference coordinate frame[J]. Journal of Geodesy and Geodynamics (in Chinese), 27(1):1-6. |
| [6] | Cheng P F, Wen H J, Cheng Y Y, et al. 2009. Parameters of the CGCS 2000 ellipsoid and comparisons with GRS 80 and WGS 84[J]. Acta Geodaetica et Cartographica Sinica (in Chinese), 38(3):189-194. |
| [7] | Featherstone W E, Dentith M C. 1997. A geodetic approach to gravity data reduction for geophysics[J]. Computer & Geosciences, 23(10):1063-1070. |
| [8] | Gao D Z. 2006. Marine gravity survey and underwater topographic correction[A]. 22nd Chinese Geophysical Annual Meeting,Abstracts(in Chinese), 350. |
| [9] | Gao J Y, Liu B H. 2014. Marine Geophysics in Offshore China (in Chinese)[M]. Beijing:Ocean Press, 86-96. |
| [10] | Hinze W J. 2003. Bouguer reduction density, Why 2.67?[J]. Geophysics, 68(5):1559-1560. |
| [11] | Hinze W J, Aiken C, Brozena J, et al. 2005. New standards for reducing gravity data:The North American gravity database[J]. Geophysics, 70(4):J25-J32. |
| [12] | Kearey P, Brooks M, Hill I. 1991. An Introduction to Geophysical Exploration[M]. 2nd ed. Blackwell Scientific Publications. |
| [13] | LaFehr T R. 1991a. Standardization in gravity reduction[J]. Geophysics, 56(8):1170-1178. |
| [14] | LaFehr T R. 1991b. An exact solution for the gravity curvature (Bullard B) correction[J]. Geophysics, 56(8):1179-1183. |
| [15] | Li B H. 1996. A discussion on the selection of elevation system in altitude correction of gravity survey[J]. Geophysical & Geochemical Exploration (in Chinese), 20(1):35-39. |
| [16] | Li X, Götze H -J. 2001. Ellipsoid, geoid, gravity, geodesy and geophysics[J]. Geophysics, 66(6):1660-1668. |
| [17] | Liu J N, Wei N, Shi C. 2013. Status and prospects of the international terrestrial reference frame (ITRF)[J]. Chinese Journal of Nature (in Chinese), 35(4):243-250. |
| [18] | Lü C C, Hao T Y, Xu Y. 2009. Complete bouguer correction in the oceanic gravity exploration[J]. Progress in Geophysics (in Chinese), 24(2):513-521, doi:10.3969/j.issn.1004-2903.2009.02.020. |
| [19] | Majumdar T J, Bhattacharyya R. 2014. High resolution satellite gravity over a part of the Sir Creek offshore on west northwest margin of the Indian subcontinent[J]. Indian Journal of Marine Sciences, 43(3):337-339. |
| [20] | Ministry of Land and Resources of the People's Republic of China. 2006. DZ/T 0082-2006, The standard for regional gravity survey (in Chinese)[S]. Beijing:Geological Publishing House. |
| [21] | Ministry of Land and Resources of the People's Republic of China. 2009. DZ/T 0247-2009, Specifications for regional marine geological survey (scale:11000000) (in Chinese)[S]. Beijing:Standards Press of China. |
| [22] | Ministry of Land and Resources of the People's Republic of China. 2014. DZ/T 0256-2014, Specifications for regional marine geological survey (scale:1250000) (in Chinese)[S]. Beijing:Standards Press of China. |
| [23] | Mohr P J, Taylor B N, Newell D B. 2008. CODATA recommended values of the fundamental physical constants:2006[J]. Reviews of Modern Physics, 80(2):633-730. |
| [24] | Moritz H. 2000. Geodetic reference system 1980[J]. Journal of Geodesy, 74(1):128-133. |
| [25] | National Imagery and Mapping Agency. 1997. Department of Defense World Geodetic System 1984:Its definition and relationships with local geodetic systems[R]. NIMA TR 8350.2, third edition. |
| [26] | National Standardization Management Committee of China. 2007. GB/T 12763.8-2007, Specifications for oceanographic survey, part 8:marine geology and geophysics survey (in Chinese)[S]. Beijing:China Standards Press. |
| [27] | National Administration of Surveying,Mapping and Geoinformation.2008. No. 2 announcement in 2008(in Chinese)[EB/OL]. http://www.sbsm.gov.cn/article/tzgg/200806/20080600037863.shtml, 2008-06-27. |
| [28] | Reynolds J M. 2011. An Introduction to Applied and Environmental Geophysics[M]. 2nd ed. Wiley-Blackwell. |
| [29] | The Defence of Mapping Agency. 1987a. Supplement to Department of Defense World Geodetic System 1984 Technical Report:Part I-Methods, techniques, and data used in WGS84 development[R]. DMA TR 8350.2-A. |
| [30] | The Defence of Mapping Agency. 1987b. Supplement to Department of Defense World Geodetic System 1984 Technical Report:Part Ⅱ-Parameters, formulas, and graphics for practical application of WGS84[R]. DMA TR 8350.2-B. |
| [31] | Tracey R, Bacchin M and Wynne P. 2007. AAGD07:A new absolute gravity datum for Australian gravity and new standards for the Australian National Gravity Database[C].//ASEG Extended Abstracts, 2007(1):1-3, doi:10.1071/ASEG2007ab149. |
| [32] | Wang B R. 1986. Gravity correction and the geophysical meaning of corresponding gravity anomaly-A discussion with Mr.Lai Zhongkang[J]. Oil Geophysical Prospecting (in Chinese), 21(1):98-104. |
| [33] | Wei Z Q. 2008a. China geodetic coordinate system 2000[J]. Journal of Geodesy and Geodynamics (in Chinese), 28(6):1-5. |
| [34] | Wei Z Q. 2008b. China geodetic coordinate system 2000 and its comparison with WGS84[J]. Journal of Geodesy and Geodynamics (in Chinese), 28(5):1-5. |
| [35] | Wen Z H, Zhang X H, Hao T Y, et al. 2014. Progress in compilation of geoscience map series for China seas and adjacent regions[J]. Chinese J. Geophys. (in Chinese), 57(12):3907-3919, doi:10.6038/cjg20141205. |
| [36] | Wong R, Rollins C and Minter C. 2012. Recent updates to the WGS 84 reference frame[C].//Proceedings of the 25th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2012), Institute of Navigation, Manassas, VA, 1164-1172. |
| [37] | Yang J Y, Zhang X H, Zhang F F, et al. 2014. Preparation of the free-air gravity anomaly map in the land and seas of China and adjacent areas using multi-source gravity data and interpretation of the gravity field[J]. Chinese J. Geophys. (in Chinese), 57(12):3920-3931, doi:10.6038/cjg20141206. |
| [38] | Yin W S, Zhang J Z. 2014. The effect of terrestrial and submarine topography on the marine gravity anomalies[J]. Progress in Geophysics (in Chinese), 29(5):2449-2455, doi:10.6038/pg20140569. |
| [39] | Zeng H L. 2008. Striking revisions of vertical datum and procedures for calculating gravity anomalies in North America[J]. Geophysical & Geochemical Exploration (in Chinese), 32(1):8-12. |
| [40] | Zheng W, Xu H Z, Zhong M, et al. 2010. Research progress in international gravity satellites and future satellite gravity measurement program in China[J]. Science of Surveying and Mapping (in Chinese), 35(1):5-9. |
| [41] | 陈俊勇. 2005.空间大地测量技术对确定地面坐标框架、地形变与地球重力场的贡献和进展——出席2005年国际大地测量协会(IAG)科学大会札记[J].地球科学进展, 20(10):1053-1058. |
| [42] | 陈俊勇. 2007.大地坐标框架理论和实践的进展[J].大地测量与地球动力学, 27(1):1-6. |
| [43] | 程鹏飞,文汉江,成英燕,等. 2009. 2000国家大地坐标系椭球参数与GRS 80和WGS 84的比较[J].测绘学报, 38(3):189-194. |
| [44] | 高金耀,刘宝华. 2014.中国近海海洋——海洋地球物理[M].北京:海洋出版社, 86-96. |
| [45] | 国家测绘局. 2008.国家测绘局2008年第2号公告[EB/OL]. http://www.sbsm.gov.cn/article/tzgg/200806/20080600037863.shtml, 2008-06-27. |
| [46] | 励宝恒. 1996.关于重力勘察的高度改正应采用何种高程系统的讨论[J].物探与化探, 20(1):35-39. |
| [47] | 高德章. 2006.海洋重力调查与海底地形改正[A].中国地球物理学会第22届年会论文集, 350. |
| [48] | 刘经南,魏娜,施闯. 2013.国际地球参考框架(ITRF)的研究现状及展望[J].自然杂志, 35(4):243-248. |
| [49] | 吕川川,郝天珧,徐亚. 2009.海洋重力勘探中的完全布格校正[J].地球物理学进展, 24(2):513-521, doi:10.3969/j.issn.1004-2903.2009.02.020. |
| [50] | 王宝仁. 1986.重力校正及相应重力异常的地球物理意义——与赖仲康同志商榷[J].石油地球物理勘探, 21(1):98-104. |
| [51] | 魏子卿. 2008a. 2000中国大地坐标系[J].大地测量与地球动力学, 28(6):1-5. |
| [52] | 魏子卿. 2008b. 2000中国大地坐标系及其与WGS84的比较[J].大地测量与地球动力学, 28(5):1-5. |
| [53] | 温珍河,张训华,郝天珧,等. 2014.我国海洋地学编图现状、计划与主要进展[J].地球物理学报, 57(12):3907-3919, doi:10.6038/cjg20141205. |
| [54] | 杨金玉,张训华,张菲菲,等. 2014.应用多种来源重力异常编制中国海陆及邻区空间重力异常图及重力场解读[J].地球物理学报, 57(12):3920-3931, doi:10.6038/cjg20141206. |
| [55] | 尹文笋,张建中. 2014.陆地和海底地形对海洋重力异常的影响[J].地球物理学进展, 29(5):2449-2455, doi:10.6038/pg20140569. |
| [56] | 曾华霖. 2008.北美国家高程基准面及重力异常计算方法的重大修改[J].物探与化探, 32(1):8-12. |
| [57] | 郑伟,许厚泽,钟敏,等. 2010.国际重力卫星研究进展和我国将来卫星重力测量计划[J].测绘科学, 35(1):5-9. |
| [58] | 中国国家标准化管理委员会. 2007. GB/T 12763.8-2007海洋调查规范,第8部分:海洋地质地球物理调查[S].北京:中国标准出版社. |
| [59] | 中华人民共和国国土资源部. 2006. DZ/T 0082-2006区域重力调查规范[S].北京:地质出版社. |
| [60] | 中华人民共和国国土资源部. 2009. DZ/T 0247-200911000000海洋区域地质调查规范[S].北京:中国标准出版社. |
| [61] | 中华人民共和国国土资源部. 2014. DZ/T 0256-2014海洋区域地质调查规范(1250000)[S].北京:中国标准出版社. |
 2015, Vol. 30
2015, Vol. 30


