GRACE(Gravity Recovery And Climate Experiment)重力卫星由美国航天局(NASA)及德国空间飞行中心(DLS)联合研发发射,采用两颗低高度(300~500 km)、近极轨道小卫星,通过精确定位和相互跟踪探测地球重力场及变化(Tapley et al.,2004a,b).GRACE卫星的主要用途包括以下三方面:
第一,确定高精度静态地球重力场的中长波部分;
第二,确定15~30天或者更长时间尺度上的地球重力场时变特征;
第三,监测、分析大气和电离层随时间的变化.
GRACE卫星每30天产出一组数据,主要有三个数据中心进行数据解算并发布相关成果:CSR(Center for Space Research,University of Texas at Austin)、GFZ(German Research Center of Geosciences)以及JPL(Jet Propulsion Laboratories).不同机构中心提供的数据产品存在不同的适用范围,目前GRACE数据集最新的产品为RL05模型.
GRACE卫星重力的优势在于能不受陆地条件的限制进行连续、快速和重复观测,由GRACE卫星重力解算得到的时变重力场信号,近年来已被广泛地应用到区域地下水储量变化及河流、冰川的质量迁移等方面的研究.在研究陆地水质量迁移方面,相较于传统的以大气和水文观测资料为基础,将地基观测、遥感卫星观测结果结合相应物理规律以及水文模式等研究而言,GRACE卫星重力能有效弥补测量范围不深,空间分布不均匀,资料获取不充分以及水文模型分布不均匀等问题造成的数据不均匀,能得到全球分布均匀,且观测尺度统一的数据(许民等,2013; Houborg et al.,2012).
GRACE重力变化数据处理中,需要将影响重力变化的固体潮、海潮、地球自转产生的极潮等潮汐成分以及大气和海洋的非潮汐成分等已知因素扣除(Bettadpur,2003; 汪汉胜等,2007).GRACE卫星重力数据经过模型校正后,得到在一定区域尺度分辨率下的非大气、非海洋的质量变化.一般认为,在季节性或更短的时间尺度上,这种剩余的重力场变化在陆地区域主要与水储量变化相关(Tapley et al.,2004a; 胡小工等,2006).陆地水储量(Terrestrial Water Storage,TWS)变化是指包含降雨、蒸发(包括蒸腾)、径流和地下水活动等过程引起的质量变化(Chen et al.,2009),在计算过程中,时变地球重力场的球谐参数转换为对地球系统表面及其浅层地下区域的质量重新分布数据,可将它理想化地假想为地球表面的一个薄层,或等效水柱高来衡量其质量变化.
近年来的研究主要应用GRACE数据估算了全球尺度、区域尺度以及多个流域尺度的水储量变化,监测冰盖质量平衡、海平面上升以及海洋环流等.由于GRACE对各种深度的水储量同样敏感,因此,也可以将其与水量平衡方程和水文模型结合来估算蒸散发量、土壤水含量和地下水储量变化等.
基于GRACE卫星重力场变化来研究中国大陆地区的陆地水储量变化,国内研究结果表明中国陆地水储量变化呈现明显的地区不平衡性和季节性变化特征(周旭华等,2006;段建宾等,2007; 邢乐林等,2007; 朱广彬等,2008; 杨元德等,2009; 钟敏等,2009; 叶叔华等,2011).对中国的几大典型流域的研究结果表明,长江流域水储量变化幅度可高达3.4 cm(胡小工等,2006; 翟宁等,2009; 许民等,2013).
GRACE卫星数据处理中,高斯平滑滤波通常是重要的处理技术,对滤波半径的选择和模型截断阶数等的选择,针对不同的研究问题有特定的要求(Chen et al.,2004,2005a,b,2006b).一般认为,高斯滤波半径为800 km时,可以有效地去除数据相关误差,获得大尺度的水文信号;当模型截断阶数为20阶时,得到的地球表面质量变化可以在保留水储量信号和模型误差之间达到较好平衡(Chen et al.,2006b).
应用GRACE卫星重力变化来进行研究之前,必须注意到滤波是对于测量误差和泄露误差的一个均衡处理,从原理上不可能完全消除这些误差(Yamamoto et al.,2007).此外,除观测误差外还有球谐系数的截断误差,特别要注意的是去“条带”和高斯平滑引起的误差在估计区域陆地水变化时,周边区域的陆地水信号会“泄露”到研究区域内,同时研究区域内的信号也可能因为高斯平滑而有所改变(Klees et al.,2008a).因此,采用GRACE卫星重力来估计陆地水储量变化只具有一定区域尺度上的平均意义,与实际陆地的定点观测结果具有十分显著的区别.下面本文将从GRACE数据反演原理、滤波处理方法、水文模型检验、陆地水储量变化应用和存在的问题等几个方面分别进行总结,最后进行综合评述和未来应用的展望.
1 数据处理方法1.1 GRACE重力数据推得地表质量重分布的基本原理地球重力场通常用大地水准面表示,大地水准面球谐系数模型为(Wahr et al.,1998)

地面物质运动引起大气水准面高度的变化为ΔN,可表示为


大地水准面球谐系数变化由两部分组成,一部分直接由地表物质引起,一部分由于固体地球产生形变而引起,表达式为




由此可得ΔClm、ΔSlm和ΔClm、ΔSlm之间存在如下关系:



由此便得到了地球表面密度变化的基本方程,转化为等效水高,则有

GRACE提供的球谐阶数是有限的,GFZ的GRACE数据中心提供了GSM数据和GAC数据的120×120阶次的月重力位球谐系数Clm和Slm(l,m≤120).UTR提供了GRACE的60×60阶次的月重力球谐系数.
由重力场的分辨率和球谐参数阶数之间的关系为

Tapley认为将模型阶数截断控制在90阶以下是合理的(Tapley et al.,2004b),Chen经进一步分析,认为大于60阶以上的数据会引入较大的误差,故通常将重力模型球谐系数截断至60×60阶次,其半波长分辨率可达到333 km(Chen et al.,2005a,b).而在利用GRACE位模型反演陆地水储量变化的实际应用中,一般模型截断阶数取至20阶(Wahr et al.,1998),能够在尽量不减少有用反演信息的同时,有效地抑制位模型误差带来的影响.
1.3 低阶参数项的处理由于GRACE的轨道几何构形对重力场的C20不敏感,故测得的C20项精度较差,然而若去除C20项会对质量变化和大地水准面高程的估算带来较大影响(Wahr et al.,1998).Chen提出其它独立于 GRACE 系统的低阶项参数与 GRACE 数据结合起来考虑,一般采用由SLR观测得到的C20项来替代(Chen et al.,2004; Cheng and Tapley,2004),大量研究采用该方法对低阶项进行了数据处理(Chen et al.,2005a,b; Seo et al.,2006; 胡小工等,2006; Yamamoto et al.,2007; 汪汉胜等,2007; 郑伟等,2012).实际运用中,也有研究考虑到该项本身就存在较大的不确定性,忽略了该项(Rodell et al.,2004b; Ramillien et al.,2005; 邢乐林等,2007; 周旭华等,2006).低阶部分中的C11、S11和C10也会对数据处理带来误差,在南极地区影响尤为明显(Chen et al.,2008),但相较于C20,其影响相对较小,部分研究中也忽略了该项的影响(Chen et al.,2007).
1.4 滤波处理方法GRACE所提供的高阶斯托克斯系数带来了大部分噪声,且阶次越高,噪声越大,如果不进行滤波平滑,则平滑结果以条带状噪声为主,无法看到陆地水储量特征(Chen et al.,2006b),此外,球谐系数的截断还产生了“截断”误差,故需要进行滤波处理来压制这种噪声,以获得更多的地球物理信号.
滤波处理是GRACE数据处理的重要步骤,目前用于消除噪声污染的滤波器大体可分为各向同性高斯滤波器(Jekeli,1981;Wahr et al.,1998)、非各向同性滤波器(Guo et al.,2010; Han et al.,2005a; Sasgen et al.,2006; Seo et al.,2006; Swenson and Wahr,2006a,b; Kusche,2007).在早期关于GRACE卫星产品的研究中,各向同性高斯滤波是常用的.后来逐渐发现GRACE误差组成并非各向同性的,仅依赖于阶的高斯滤波无法有效的去除信号误差,因此提出了用非各向同性高斯滤波方法(Han et al.,2005a)、去相关滤波器方法(Swenson and Wahr,2006a)等来处理GRACE数据,通过这种方法来消除“南北”条带误差和球谐系数的相关误差.以下介绍几个常用的滤波器的原理以及滤波参数的选择.
1.4.1 各向同性高斯滤波器在大地水准面的球谐系数展开式(Wahr et al.,1998)的基础上,Swenson等人引入了高斯平滑算子W(γ)(Swenson and Wahr,2002),推得了地表质量的变化,W(γ)表示为

 ,r为高斯平滑半径,a为地球平均半径,γ为点(θ,λ)与点(θ′,λ′)之间的夹角.W随γ的变化而变化.经过高斯平滑后,Δσ变为
,r为高斯平滑半径,a为地球平均半径,γ为点(θ,λ)与点(θ′,λ′)之间的夹角.W随γ的变化而变化.经过高斯平滑后,Δσ变为
 ,由此可得等效水高(常用cm表示)为
,由此可得等效水高(常用cm表示)为
而高斯平滑半径的选择与误差水平之间具有一定的关系,研究结果表明选择较大的高斯平滑半径,虽可以降低误差,但如果平滑半径超过实验区域过多,将引入不必要的误差(Werth et al.,2009).因此,需选择合适的滤波半径,使得在减少误差和噪声污染的同时,又不损失有效的地表质量变化的信息.
通过对高斯滤波半径的选取的研究表明800 km高斯平滑半径更适合于对陆地水储量的研究(Chen et al.,2005b;邹正波等,2008),大尺度的特征可以较为显著的表现出来,并结合GLDAS数据得出了全球几大流域尺度水储量的季节性变化(Chen et al.,2007).图 1对GRACE数据分别进行400 km、600 km、800 km和1000 km的高斯滤波处理,可看出400 km滤波半径时条带噪声较大,600 km滤波半径时噪声相对较小,但在海洋区域仍然明显,1000 km滤波半径时对噪声的处理相对较好,却损失了部分真实信号.
 | 图 1 2003年4月全球陆地水储量的变化(平均海平面变化单位为cm),(a)(b)(c)(d)平滑半径分别为400 km,600 km,800 km,1000 km(Chen et al.,2005b) Fig. 1 Global terrestrial water storage changes (in units of cm of equivalent water thicknesschange) in April 2003 when Gaussian smoothing with spatial scale of 400 (Figure 1a), 600 (Figure 1b),800 (Figure 1c), or 1000 km (Figure 1d) is applied(Chen et al.,2005b) |
平滑半径较大的高斯滤波器虽然能压制高阶噪声,但高斯滤波只考虑了阶部分,对次部分不起作用,因此通过改进提出了非各向同性滤波器,它与球谐系数的阶数和次数均有关(Han et al.,2005a).它基于对系数的经验性分析或用一个先验模型来进行观测,能有效去除条带现象(Kusche,2007; Klees et al.,2008a).各向异性高斯滤波器表示为


图 2中显示了平滑半径为r1=1000 km高斯滤波(a)和非各向同性高斯滤波(b)r0=500 km,r1=1000 km,m=15的谱.可以看到非各向同性高斯滤波能够有效地滤除高阶以及低次位系数,并且能够拒绝高次系数.但是随着阶数的增高,发现非各向同性高斯滤波的频谱会出现负值(Han et al.,2005a).
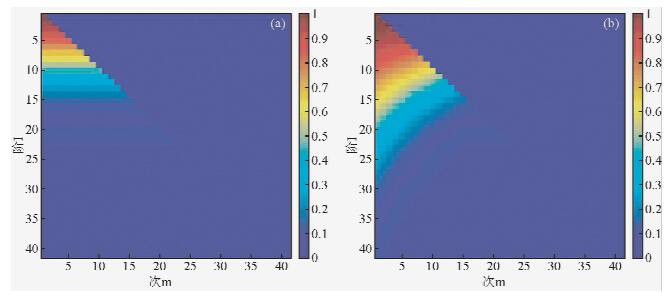 | 图 2 (a)各向同性高斯(r=1000 km)滤波;(b)非各向同性高斯滤波(r0=500 km,r1=1000 km,m1=15)(Han et al.,2005a) Fig. 2 (a) Gaussian(r=1000 km)filter;(b) non-isotropic filter(r0=500 km,r1=1000 km,m1=15) (Han et al.,2005a) |
高斯滤波和各向异性滤波的处理虽然都能够减少球谐系数带来的误差,但并没有考虑到球谐系数间存在的相关性,Swenson设计了去相关滤波来消除球谐系数间的相关系统误差,该方法又被称为PnMm方法(Swenson and Wahr,2006a).其基本思想是前m×m阶的位系数保持不变,用n阶多项式对大于等于m阶次的位系数进行拟合,奇数阶与偶数阶分开拟合.
图 3c与3a对比发现,经过该相关误差滤波后,条纹明显地减少,但在赤道附近区域该效果不是很明显;图 3c 经过了500 km 高斯平滑,依然存在条纹现象;而图 3d 显示经去相关滤波和500 km 高斯平滑后,条纹现象已经非常少.因此可得出相关误差滤波能够有效的减少南北向的条纹噪声.
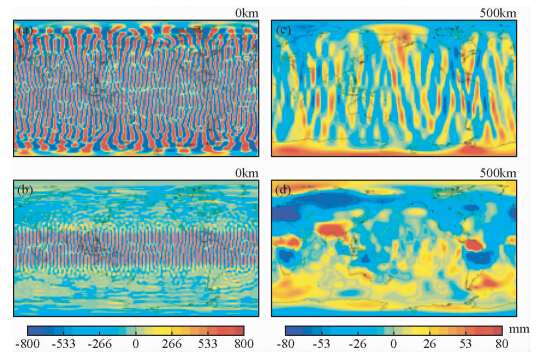 | 图 3 GRACE 全球月水储量异常图,(a)未经任何滤波,(b)去相关误差滤波,未经过高斯平滑;(c)未经过去相关滤波,500 km 高斯平滑;(d)去相关滤波和 500 km 高斯平滑 (Swenson and Wahr,2006a) Fig. 3 GRACE-derived maps of monthly anomaly of water storage. (a) Unfiltered, no smoothing; (b)filtered with correlated-error filter, no smoothing; (c) unfiltered and smoothed with 500 km Gaussian; (d) filtered with correlated-error filter and smoothed with 500 km Gaussian(Swenson and Wahr,2006a) |
为了平衡噪声和真实地球物理信号,还需要选取合适的滤波参数(Swenson et al.,2006; Belda et al.,2015).去相关滤波方法一般不单独使用,而是结合高斯滤波方法(Chen et al.,2007; 杨元德等,2009; 鄂栋臣等,2009; 金涛勇等,2010)或Fan滤波的方法(罗志才等,2012; 李琼等,2013; 鞠晓蕾等,2013)使用,以更有效地抑制条带噪声.
1.4.4 滤波方法的选取除以上常用空间滤波器之外,不同研究者也给出了不同的滤波方法.如:维纳滤波,它是一种线性卷积低通滤波,通过分别计算信号和噪声的方差,使得滤波后的结果函数误差尽可能小(Wiener,1964; Sasgen et al.,2006).Chen提出了最优平滑方法对全球水储量进行了估计,并与高斯平滑对比表明该方法更能有效去除高阶误差(Chen et al.,2006b).之后又提出两步滤波法来减小高阶噪声(Chen et al.,2008,2009).Klees提出了一个能减小GRACE月数据误差的ANS滤波方法,它既是各项异性的,又是非对称的(Klees et al.,2008a).全球水文模型先验信息滤波技术(Ramillien et al.,2005)、方向滤波(Han et al.,2005a)、次卷积方法(Kusche et al.,2009)以及Fan滤波器(Zhang et al.,2009)也同样能有效抑制球谐系数的高阶噪声.经验正交函数(EOF)方法能将球谐系数进行分离以去除高阶噪声,该方法也得到了广泛应用(Wouters and Schrama,2007; Neumeyer et al.,2008; Schmidt et al.,2008).
不同学者对于不同研究区域选取了对应适合的最佳滤波器和滤波参数以压制噪声并得到更多地球物理信号.Swenson通过估算滤波器造成的误差值,建议依据不同流域的特征,如地球物理位置、形状和流域水文信号等特征来选择适合该最佳滤波类型及滤波器参数(Swenson et al.,2006),Werth就6种不同类型的滤波器进行对比分析,也提出相同建议(Werth et al.,2009).
2 水文模型检验GRACE监测重力变化结果相对容易验证,可直接的地面重力监测数据进行对比.然而,GRACE估算水储量则欠缺直接的监测数据进行对比,这是因为GRACE计算得到的水储量变化时空间尺度上的总水储量变化,包括地下水、土壤水含量、地表水、冰雪和生物含水量,目前常用水文数据模型进行检验,此外也可以应用GPS等对GRACE数据模型进行验证(王正涛等,2008; 廖海华等,2010; 王武星等,2010),和结合绝对重力仪(邢乐林等,2012)或超导重力仪(Neumeyer et al.,2008; 周江存等,2009)数据对GRACE水储量估计进行验证等.
水文模型可以作为验证GRACE结果精确度的主要方式,同样地,利用GRACE陆地水储量数据也可以对全球水文模型进行改进(Rowlands et al.,2005; Niu and Yang,2006a).水文模型主要分为两类,陆面过程模型(L and Surface Model,LSM)和水平衡模型(Water Budget Model,WBM).陆面过程模型主要表达气候模型和天气数值预测对陆地表面的影响等(Rodell et al.,2004a);水平衡模型(Güntner,2008)则主要考虑河流流域区域的水流量.目前常用GLDAS(Global L and Data Assimilation System)、CPC(Climate Prediction Center)以及WGHM(Watergap Global Hydrological Model)数据来验证GRACE水储量估测.
GLDAS是由美国国家航空航天局(NASA)戈达德空间飞行中心(GSFC)和美国海洋和大气局(NOAA)国家环境预报中心(NCEP)联合开发的水储量模型,是一个全球高分辨率路面模拟系统,融合来自地面和卫星的观测数据提供最优化的近实时的地表状态变量.GLDAS所预测的陆地水储量变化只包括土壤水分和地表积雪变化,地下水变化不在其内,其时间间隔为3小时或者一个月,来自于四个LSM模型:Catchment、Noah、CLM(Community L and Model)和VIC(Variable Infiltration Capacity).产品空间格网间隔分为0.25°与1°两种.其中0.25°格网间隔的产品从2000年2月至今,1°格网间隔产品时间跨度从1979年至今,但GLDAS缺乏南极数据.目前被广泛运用于GRACE结果的验证,表明GRACE卫星数据能够足够精确的检测到较大流域水储量的变化量.
CPC水文模型主要反映了土壤水分和积雪变化,它来自美国国家海洋和大气局(NOAA)的气象预报中心(CPC).主要根据全球观测到的降水分布而建立,采用的数据包括CPC每日和每小时的降水分析结果、太阳辐射分布、地表大气压、潮湿度、温度以及水平风速等.CPC提供的产品包括地表积雪分布以及厚度,土壤湿度,地表以下4层的土壤水含量等,时间间隔为1个月,经、纬度格网为0.5°×0.5°,时间跨度从1948年至今.CPC水文模型同样不含南极数据.
WGHM水文模型模型不仅计算了各个国家或流域的长期平均水资源,还研究了土壤水、径流、地下水补给、地表积雪和地表水储量(包括河流、湖泊、水库)变化,空间分辨率为0.5°×0.5°.与GRACE数据结合分析,能有效验证GRACE对水储量的估计(Schmidt et al.,2006; Ramillien et al.,2005,2006; Kusche et al.,2009).
为了对GRACE结果进行验证,GLDAS、CPC和WGHM数据需进行球谐展开,并进行相应的“条带”处理和平滑处理.大量研究结果表明GRACE与水文模式具有很好的一致性,但相较于水文模式而言,GRACE包含的信号明显比水文模型多,因为GRACE资料不仅包含了地表土壤水,还包括了土壤水、湖泊水、地下水以及湿地的影响.结合GRACE与GLDAS的陆地水储量估算值,分析其差别在于遗漏表面和地下水成分或雪参数化不足(Syed et al.,2008).Winsemius利用GRACE卫星估算赞比西河上游的水储量时变量,通过模型LEW(Lumped Elementary Watershed)验证其结果,并讨论了偏差来源以及提高GRACE时空分辨率的措施(Winsemius et al.,2006).Zaitchik结合LSM模型,通过对密西西比河以及四个子河流的水储量分析中证实了数据同化在水储量研究中的重要性(Zaitchik et al.,2008).同时,结合CLSM水文模型,还可监测区域尺度的干旱事件(Houborg et al.,2012).此外,研究还发现GRACE所得平均水储量变化和水文模型数据在年际尺度上虽具有一致性,但GRACE观测结果迟滞了两个月左右(Papa et al.,2008),这主要是因为陆地水包括了该流域内的该月之前的降雨部分(Feng et al.,2013).
3 陆地水储量变化估算研究进展3.1 全球尺度水储量变化通过数值模拟去除大气和海洋引起的干扰信号即可得到陆地水储量的变化.研究表明在季节性时间尺度和几百千米或更大空间尺度上,GRACE可探测到平均小于 1 cm(Wahr et al.,2004; Swenson et al.,2003)甚至0.9 mm的等效水高变化(Andersen et al.,2005).
Tapley(Tapley et al.,2004b)利用GRACE数据得到了全球以及南美洲水量变化;Chen和胡小工等就CSR提供的2002年到2003年间的15个月的数据,分别用800 km高斯平滑并结合GLDAS水文模型(Chen et al.,2005)和1000 km高斯平滑并结合CPC和GLDAS水文模型相比较(胡小工等,2006),得到了全球水储量的变化.GRACE数据反演得到的平均水储量和水文模型所得的结果符合的相当好,且呈现明显的季节性特征.从图 4和图 5的比较中看出,二者的不同集中在海洋上,这是由于图 5在计算过程中加回了已扣除的大气和海洋影响.对比发现在大陆地区的变化是一致的,基本体现出大陆地区水储量的变化.
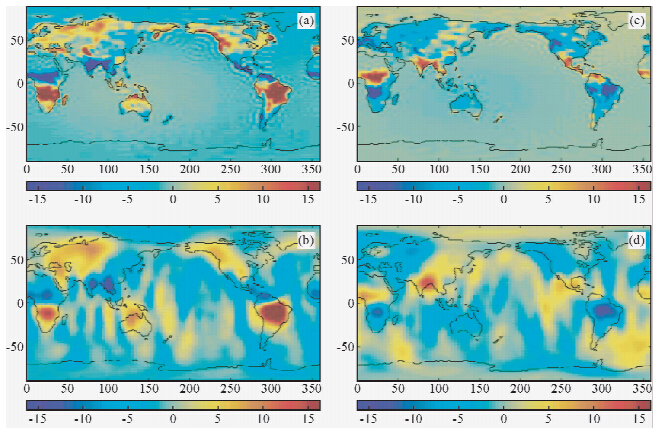 | 图 4 GLDAS未经高斯平滑所得的陆地水储量在(a)2003年4月(b)2003年10月的变化;GRACE数据经800 km高斯滤波估测的全球水储量变化(c)2003年4月(d)2003年10月(Chen et al.,2005a) Fig. 4 Continental water storage change in (a) April and (b) October 2003 estimated from GLDASwith no smoothing,and GRACE estimated global water storage change in (c) April and (d) October 2003, with 800 km smoothing. To be consistent with GRACE data processing, C20 and the degree-1 spherical harmonics are also removed from GLDAS data.(Chen et al.,2005a) |
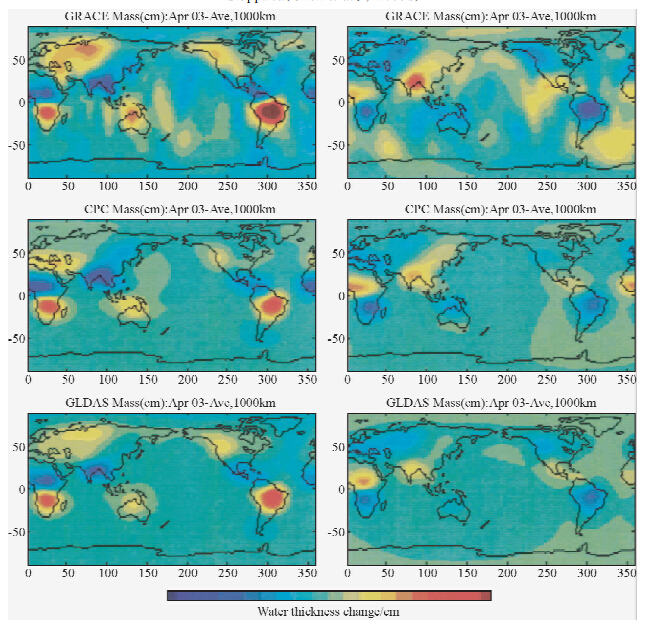 | 图 5 GRACE反演的2003年3月和10月的全球水储量变化,以及GLDAS与CPC两个水文模型(Hu et al.,2006) Fig. 5 GRACE recovery of the water storage in March 2003 and October 2003 (upper two panels), and two state-of-the-art hydrology models. CPC model (middle) and GLDAS (lower). Units are cm of equivalent water height(Hu et al.,2006) |
虽然与水文模型均符合较好,但实质差异仍然是明显的,从图 4和图 5均可看出在海洋地区差异较大,如南美洲的亚马逊河流域、非洲大陆的尼日尔胡、乍得和赞比西河流域,亚洲东南部的孟加拉湾和长江流域地区以及澳大利亚北部.这可能是由两种原因引起的.一方面,GRACE重力观测数据以及在数据分析中带来的误差;另一方面,由于当前的水文模型可能仍然不完善,即未能正确反映水储量的变化.但毫无疑问GRACE卫星重力数据能揭示全球的水储量变化.
3.2 区域尺度水储量变化GRACE卫星数据也被应用于监测区域尺度的水储量变化,对区域水储量进行分析可达2cm的等效水高(Klees et al.,2008b).通过择取合适的滤波方法并结合水文模型分析获取美国地区高地平原含水层的季节性陆地水储量(Strassberg et al.,2007)、Illinois地区的陆地水储量变化(Swenson et al.,2006; Yeh et al.,2006)以及北极地区雪水储量(Niu et al.,2007);结合测井资料获取了中欧地区2002-2003年间的陆地水储量年际变化(Andersen et al.,2005).另外,通过获得区域水储量并运用平衡方程(降雨量-土壤水分蒸发蒸腾-地表流失-深层渗透=土壤水分变化+积雪变化),可求得蒸散发量(Ramillien et al.,2006; Niu and Yang,2006b; Yeh et al.,2008)、渗透量、土壤水含量和地下水变化量(Niu and Yang,2006b; Yeh et al.,2006; Swenson et al.,2008; Strassberg et al.,2009).并获取了California地区(Famiglietti et al.,2011)和印度(Rodell et al.,2009; Tiwari et al.,2009)的地下水亏损量.结合遥感数据获得了中东地区中北部的地下水亏损(Voss et al.,2013).但GRACE数据因受其空间分辨率限制,区域尺度越小,误差越大.
国内大量学者也对中国及其周边地区的水储量变化进行了估测(邢乐林等,2007; 段建斌等,2007; 朱广彬等,2008; 苏晓莉等,2009; 胡小工等,2006; 杨元德等,2009).监测了2003年~2007年连续5年来中国区域陆地水储量的线性变化趋势,得出我国水储量变化幅度趋势较大的有五大典型地区(华北京津冀地区、青藏高原区域、三峡水库区、青川甘交界区域以及新疆地区)的水储量变化(钟敏等,2009).利用87个月的GRACE时变重力数据,采用13点滑动年平均去除了季节性变化解释了中国及其周边陆地水储量季节性变化的特征(叶叔华等,2011).图 6a 呈现出2003-2009年中国地区水储量的区域不平衡性,图 6b呈现出明显的季节变化特征.
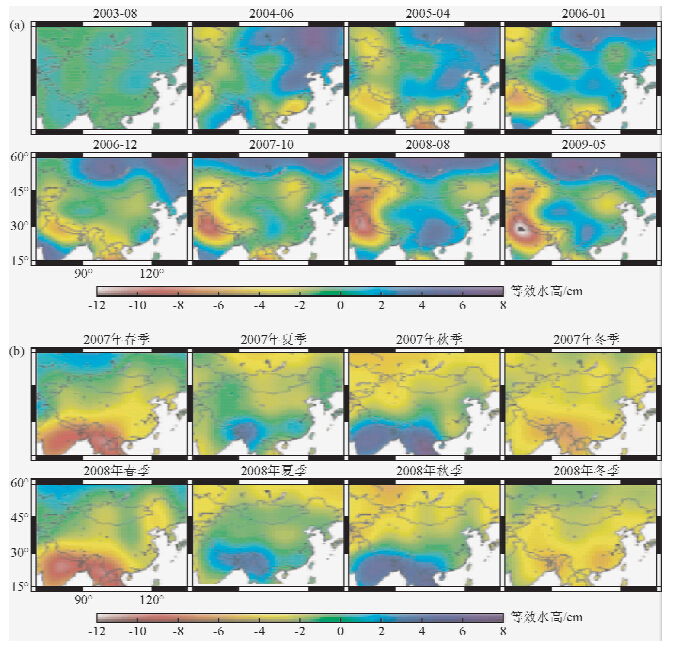 | 图 6 中国及其周边地区以水高形式表示的(a)陆地水量的趋势变化及(b)季节性变化(叶叔华等, 2011) Fig. 6 The trend (a) and seasonal changes (b) of water storage variation in water sickness in China and adjacent regions(Ye et al., 2011) |
针对地下水亏损较严重的华北平原,也证实了GRACE水储量估测结果与民用及灌溉所用的地下水抽取相情况相符合(苏晓莉等,2012; 邢乐林等,2012);并结合GBCNP(Groundwater Bulletin of China Northern Plains)分析得到含水层以及山脉区域对地下水估测有影响(Feng et al.,2013).新疆天山山区由于气候变暖、冰川消融等原因水储量变化复杂,结合国家气象台逐月降水资料,采用趋势分析法,得到该地区8年以来的水储量变化呈下降趋势(许民等,2013).GRACE数据还用于研究青藏高原及雅鲁藏布江流域的水储量的衰减趋势(许朋琨和张万昌,2013)以及我国2009年到2010年的西南干旱事件(李琼等,2013)等.
3.3 流域尺度水储量变化对流域水储量的处理,需要考虑到降雨、蒸发、地表径流、土壤与地下水的交换等多种过程的总和.运用陆地上每点的积雪厚度、土壤水分以及由GRACE反演获得的总水储量变化,结合水储量的平衡方程,即可求得流域水储量.
大量学者将GRACE应用于估测流域的水储量变化,但由于其空间分辨率的限制(Yamamoto et al.,2007),目前主要集中于面积较大的流域,如亚马逊流域(Tapley et al.,2004a; Chen et al.,2005a; Syed et al.,2008; Ramillien et al.,2005; Rodell et al.,2007)、密西西比河流域流域(Syed et al.,2005; Wahr et al.,2004; Swenson et al.,2003; Chen et al.,2007)、尼罗河流域(Frappart et al.,2008)等区域,其精度可达1.0~1.5cm等效水柱高(Velicogna and Wahr,2006).GRACE卫星数据对于大尺度区域严重干旱和洪灾事件也具有监测能力(Chen et al.,2010; Reager and Famiglietti,2009),研究表明全球几大流域(密西西比河流域、亚马逊河流域、刚果河流域、鄂毕河流域、赞比西河流域以及维多利亚流域)的年际水储量均呈现明显的季节性变化.此外,Crowley运用GRACE数据与降雨资料(CMAP,TRMM)对比分析横跨赤道两侧的刚果河流域的水储量变化,得出由于径流量而导致亚马逊流域和刚果和流域的水储量残差呈现负相关变化(Crowley et al.,2006).结合水量平衡方程和水文模型,还可以估算地下水储量(Rodell et al.,2007)、土壤含水量(Rodell and Famiglietti,2001)、蒸散发(Rodell et al.,2004b; Swenson and Wahr,2006b)、以及河流流量(Syed et al.,2009).
GRACE地球重力场模型也在国内几个大的典型流域的研究中得到了运用,如长江流域(胡小工等,2006; 许民等,2013; 翟宁等,2009)、海河流域(Moiwo et al.,2009、黑河流域(曹艳萍和南卓铜,2011; 罗志才等,2012)等区域水储量变化的监测.在更小尺度区域水储量变化方面也有研究,汪汉胜证明了GRACE重力反演数据对于三峡库区的监测是合理的(汪汉胜等,2007),并结合WGHM模型反演了三峡水库补给水系的水储量变化(Wang et al.,2011).将GRACE数据模型与水文模型相比较发现两者有较好的吻合,且都呈现出明显的季节性变化.
4 目前研究存在的主要问题GRACE重力卫星对于水储量的估计具有重要作用,但所获取的GRACE数据存在误差.误差来源主要包括两大类:球谐系数引起的误差、信号泄露引起的误差.且误差随着测量区域的尺度大小、纬度以及模型而改变(Seo et al.,2006).
4.1 球谐系数误差球谐系数引起的误差主要包括仪器误差、数据处理误差和混淆效应.
仪器误差即卫星间距离变化率的系统噪声误差、加速度误差、超稳定振荡器误差和轨道误差.GRACE反演地球重力场的精度由GRACE误差决定,随着球谐系数阶数的增加,可以通过截断阶数和空间平均来减少该误差的影响(Swenson and Wahr,2002),这样既能估算任意地区的水储量变化,又能将卫星测量误差控制在信号泄露误差的可接受范围内.但阶数截断会产生“截断”误差,此外,为抑制球谐系数高阶噪声而引入的滤波处理也会带来误差,研究表明,纬度和平滑半径相关的误差呈正太分布(Wahr et al.,2006).
混淆误差是指重力场中那些次级的短周期变化混入月平均重力场而导致的误差.反演地球时变重力场时,假定海洋潮汐和大气影响是已知的,利用模型化的数据移去固体地球、海洋潮汐、大气质量变化在陆地上的影响,理论上,如果这些模型是完美的,GRACE球谐系数中剩余的时变信号只是由于陆地水储量变化引起的,但实际上,大气-海洋去混淆模型(AOD)本身存在误差,这些模型中误差都会导致与重力场模型中存在混淆误差(Seo et al.,2006).这将会引起错误的潮汐模拟和不正确的卫星轨道的大气扰动,影响反演重力场的精度.Han等(Han et al.,2004)通过模拟海洋潮汐、大气和陆地水储量的时变混淆对GRACE卫星月轨道造成的扰动来评估实际混淆效应,提出定量化GRACE重力场中数据和地球物理模型来消除与球谐系数相关的混淆误差.
4.2 信号泄漏误差信号泄漏误差是指研究区域外的地球物理信号进入了研究区域内,或者研究区域内的信号未考虑完全,对于小尺度区域的研究尤为明显(Baur et al.,2009),且通常由所监测流域的尺度大小以及纬度来决定(Seo et al.,2006).常用滤波处理(如均值函数、高斯滤波、最佳平滑核)来减少信号泄露,通过选取最优平滑核能最大程度的减少信号泄漏误差(Wahr et al.,2004),在区域尺度的研究中,空间波谱定位法(Longuevergne et al.,2010; Rodell and Famiglietti,2002)的提出也可用于去除信号泄露误差以及有混淆误差,并用此方法获取了美国高原含水层的水量变化.分析GRACE重力场数据及格林兰岛质量平衡时,Velicogna结合GLDAS-Noah陆表模型估算来自格林兰岛外的陆地水文信号污染值,并利用GLDAS和CPC估算值之差作为水文泄露测量的不确定值(Velicogna and Wahr,2005),从GRACE重力场中去除了水文泄露值估测了南极地区质量的亏损(Velicogna and Wahr,2006).此外,各向异性高斯滤波器也能有效去除泄露误差(Guo et al.,2012).需要考虑的还有冰后回弹(Velicogna and Wahr,2005; 汪汉胜等,2009)带来的误差.
5 结论与展望5.1 GRACE重力卫星数据在多个学科领域得到了广泛应用,尤其在陆地水储量应用研究中取得了重大进展,有助于分析和了解全球水质量平衡以及大气、陆地、海洋、冰盖之间的水交换.利用GRACE重力数据可估测全球尺度及大尺度区域的陆地水储量变化,在水文研究方面估测地下水、土壤水分蒸发蒸腾损失总质量的大尺度变化,有助于对大尺度水文模型的发展评价,并改善现有水文模型.
5.2 通过对滤波方法分析、滤波参数及模型截断阶数选择等具体问题的探讨,得出非各向异性滤波器相对地能更有效地消除GRACE数据误差.国内外研究表明,利用GRACE位模型可推求全球陆地水储量月变化和年际变化,且与水文模型资料相比,结果显示在南美洲的亚马逊河流域、非洲大陆的尼日尔湖、乍得和赞比西河流域、亚洲东南部的孟加拉湾和长江流域地区以及澳大利亚北部等区域符合较好.结合水文资料对中国地区的陆地水储量变化分析,表明中国大陆地区的陆地水储量变化呈现出明显的地区不平衡性和季节性变化特征,可见利用GRACE反演数据监测区域陆地水储量变化已成为独特而有效的技术手段.
5.3 但GRACE数据由于空间分辨率不足,在小区域尺度和小流域尺度的水储量变化监测计算结果与实际情况误差较大.此外,由于水文模型本身不够完善,全球水文信号变化缺乏真实而独立的观测等问题,无法正确解释GRACE观测得到的水文信号.相信随着GRACE-Follow-On计划的实施,能够提高对水储量变化的监测精度,并在气候变化、陆地冰川变化、模型数据同化以及地下水资源的利用等方面发挥积极作用.在未来的应用研究中,近一步提升GRACE的空间分辨率,将能弥补由GRACE的空间分辨率带来的误差,从而推动GRACE卫星在陆地水储量变化监测中的研究和应用.
致 谢 感谢审稿专家的热情支持和帮助!
| [1] | Andersen O B, Seneviratne S I, Hinderer J, et al. 2005. GRACE-derived terrestrial water storage depletion associated with the 2003 European heat wave[J]. Geophysical Research Letters, 32(18):L18405. |
| [2] | Baur O, Kuhn M, Featherstone W E. 2009. GRACE-derived ice-mass variations over Greenland by accounting for leakage effects[J]. Journal of Geophysical Research:Solid Earth (1978-2012), 114(B6):B06407. |
| [3] | Belda S, García-García D, Ferrándiz J M. 2015. On the decorrelation filtering of RL05 GRACE data for global applications[J]. Geophysical Journal International, 200(1):173-184. |
| [4] | Bettadpur S. 2003. Level-2 gravity field product user handbook[R]. GRACE 327-734, The GRACE Project. |
| [5] | Chen J L, Rodell M, Wilson C R, et al. 2005a. Low degree spherical harmonic influences on Gravity Recovery and Climate Experiment (GRACE) water storage estimates[J]. Geophysical Research Letters, 32(14):L14405. |
| [6] | Chen J L, Tapley B D, Wilson C R. 2006a. Alaskan mountain glacial melting observed by satellite gravimetry[J]. Earth and Planetary Science Letters, 248(1-2):368-378. |
| [7] | Chen J L, Wilson C R, Famiglietti J S, et al. 2005b. Spatial sensitivity of the Gravity Recovery and Climate Experiment (GRACE) time-variable gravity observations[J]. Journal of Geophysical Research:Solid Earth (1978-2012), 110(B8):B08408. |
| [8] | Chen J L, Wilson C R, Famiglietti J S, et al. 2007. Attenuation effect on seasonal basin-scale water storage changes from GRACE time-variable gravity[J]. Journal of Geodesy, 81(4):237-245. |
| [9] | Chen J L, Wilson C R, Seo K W. 2006b. Optimized smoothing of Gravity Recovery and Climate Experiment (GRACE) time-variable gravity observations[J]. Journal of Geophysical Research:Solid Earth (1978-2012), 111(B6):B06408. |
| [10] | Chen J L, Wilson C R, Tapley B D, et al. 2004. Low degree gravitational changes from GRACE:validation and interpretation[J]. Geophysical Research Letters, 31(22):L22607. |
| [11] | Chen J L, Wilson C R, Tapley B D, et al. 2008. Antarctic regional ice loss rates from GRACE[J]. Earth and Planetary Science Letters, 266(1-2):140-148. |
| [12] | Chen J L, Wilson C R, Tapley B D, et al. 2009. 2005 drought event in the Amazon River basin as measured by GRACE and estimated by climate models[J]. Journal of Geophysical Research:Solid Earth (1978-2012), 114(B5):B05404. |
| [13] | Chen J L, Wilson C R, Tapley B D. 2010. The 2009 exceptional Amazon flood and interannual terrestrial water storage change observed by GRACE[J]. Water Resources Research, 46(12):W12526. |
| [14] | Cheng M K, Tapley B D. 2004. Variations in the Earth's oblateness during the past 28 years[J]. Journal of Geophysical Research:Solid Earth (1978-2012), 109(B9):B09402. |
| [15] | Crowley J W, Mitrovica J X, Bailey R C, et al. 2006. Land water storage within the Congo Basin inferred from GRACE satellite gravity data[J]. Geophysical Research Letters, 33(19):L19402. |
| [16] | E D C, Yang Y D, Zhao D B. 2009. The sea level change from the Antarctic ice sheet based on GRACE[J]. Chinese Journal of Geophysics (in Chinese), 52(9):2222-2228, doi:10.3969/j.issn.0001-5733.2009.09.005. |
| [17] | Famiglietti J S, Lo M, Ho S L, et al. 2011. Satellites measure recent rates of groundwater depletion in California's Central Valley[J]. Geophysical Research Letters, 38(3):L03403. |
| [18] | Feng W, Zhong M, Lemoine J M, et al. 2013. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground-based measurements[J]. Water Resources Research, 49(4):2110-2118. |
| [19] | Frappart F, Papa F, Famiglietti J S, et al. 2008. Interannual variations of river water storage from a multiple satellite approach:A case study for the Rio Negro River basin[J]. Journal of Geophysical Research:Atmospheres (1984-2012), 113(D21):D21104. |
| [20] | Güntner A. 2008. Improvement of global hydrological models using GRACE data[J]. Surveys in Geophysics, 29(4-5):375-397. |
| [21] | Guo J Y, Duan X J, Shum C K. 2010. Non-isotropic Gaussian smoothing and leakage reduction for determining mass changes over land and ocean using GRACE data[J]. Geophysical Journal International, 181(1):290-302. |
| [22] | Han S C, Jekeli C, Shum C K. 2004. Time-variable aliasing effects of ocean tides, atmosphere, and continental water mass on monthly mean GRACE gravity field[J]. Journal of Geophysical Research:Solid Earth (1978-2012), 109(B4):B04403. |
| [23] | Han S C, Shum C K, Jekeli C, et al. 2005a. Non-isotropic filtering of GRACE temporal gravity for geophysical signal enhancement[J]. Geophysical Journal International, 163(1):18-25. |
| [24] | Han S C, Shum C K, Jekeli C, et al. 2005b. Improved estimation of terrestrial water storage changes from GRACE[J]. Geophysical Research Letters, 32(7):L07302. |
| [25] | Houborg R, Rodell M, Li B L, et al. 2012. Drought indicators based on model-assimilated Gravity Recovery and Climate Experiment (GRACE) terrestrial water storage observations[J]. Water Resources Research, 48(7):W07525. |
| [26] | Jekeli C. 1981. Alternative methods to smooth the Earth's gravity field[R]. Technical Report Rep 327.Columbus:Department of Geodesy and Science and Surveying, Ohio State University. |
| [27] | Jin T Y, Li J C, Wang Z T, et al. 2010. Global ocean mass variation in recent four years and its spatial and temporal characteristics[J]. Chinese Journal of Geophysics (in Chinese), 53(1):49-56, doi:10.3969/j.issn.0001-5733.2010.01.006. |
| [28] | Ju X L, Shen Y Z, Zhang Z Z. 2013. Antarctic ice mass change analysis based on GRACE RL05 data[J]. Chinese Journal of Geophysics (in Chinese), 56(9):2918-2927, doi:10.6038/cjg20130906. |
| [29] | Klees R, Revtova E A, Gunter B C, et al. 2008a. The design of an optimal filter for monthly GRACE gravity models[J]. Geophysical Journal International, 175(2):417-432. |
| [30] | Klees R, Liu X, Wittwer T, et al. 2008b. A comparison of global and regional GRACE models for land hydrology[J]. Surveys in Geophysics, 29(4-5):335-359. |
| [31] | Kusche J. 2007. Approximate decorrelation and non-isotropic smoothing of time-variable GRACE-type gravity field models[J]. Journal of Geodesy, 81(11):733-749. |
| [32] | Kusche J, Schmidt R, Petrovic S, et al. 2009. Decorrelated GRACE time-variable gravity solutions by GFZ, and their validation using a hydrological model[J]. Journal of Geodesy, 83(10):903-913. |
| [33] | Li Q, Luo Z C, Zhong B, et al. 2013. Terrestrial water storage changes of the 2010 southwest China drought detected by GRACE temporal gravity field[J]. Chinese Journal of Geophysics (in Chinese), 56(6):1843-1849, doi:10.6038/cjg20130606. |
| [34] | Liao H H, Zhong M, Zhou X H. 2010. Climate-driven annual vertical deformation of the solid Earth calculated from GRACE[J]. Chinese Journal of Geophysics (in Chinese), 53(5):1091-1098, doi:10.3969/j.issn.0001-5733.2010.05.009. |
| [35] | Longuevergne L, Scanlon B R, Wilson C R. 2010. GRACE Hydrological estimates for small basins:Evaluating processing approaches on the High Plains Aquifer, USA[J]. Water Resources Research, 46(11):W11517. |
| [36] | Moiwo J P, Yang Y H, Li H L, et al. 2009. Comparison of GRACE with in situ hydrological measurement data shows storage depletion in Hai River basin, Northern China[J]. Water SA, 35(5):663-670. |
| [37] | Neumeyer J, Barthelmes F, Kroner C, et al. 2008. Analysis of gravity field variations derived from superconducting gravimeter recordings, the GRACE satellite and hydrological models at selected European sites[J]. Earth Planets and Space, 60(5):505-518. |
| [38] | Niu G Y, Yang Z L. 2006a. Assessing a land surface model's improvements with GRACE estimates[J]. Geophysical Research Letters, 33(7):L07401. |
| [39] | Niu G Y, Yang Z L. 2006b. Effects of frozen soil on snowmelt runoff and soil water storage at a continental scale[J]. Journal of Hydrometeorology, 7(5):937-952. |
| [40] | Niu G Y, Yang Z L, Dickinson R E, et al. 2007. Development of a simple groundwater model for use in climate models and evaluation with Gravity Recovery and Climate Experiment data[J]. Journal of Geophysical Research:Atmospheres (1984-2012), 112(D7):D07103. |
| [41] | Papa F, Güntner A, Frappart F, et al. 2008. Variations of surface water extent and water storage in large river basins:A comparison of different global data sources[J]. Geophysical Research Letters, 35(11):L11401. |
| [42] | Ramillien G, Frappart F, Cazenave A, et al. 2005. Time variations of land water storage from an inversion of 2 years of GRACE geoids[J]. Earth and Planetary Science Letters, 235(1-2):283-301. |
| [43] | Ramillien G, Lombard A, Cazenave A, et al. 2006. Interannual variations of the mass balance of the Antarctica and Greenland ice sheets from GRACE[J]. Global and Planetary Change, 53(3):198-208. |
| [44] | Reager J T, Famiglietti J S. 2009. Global terrestrial water storage capacity and flood potential using GRACE[J]. Geophysical Research Letters, 36(23):L23402. |
| [45] | Rodell M, Chen J L, Kato H, et al. 2007. Estimating groundwater storage changes in the Mississippi River basin (USA) using GRACE[J]. Hydrogeology Journal, 15(1):159-166. |
| [46] | Rodell M, Famiglietti J S. 2001. An analysis of terrestrial water storage variations in Illinois with implications for the Gravity Recovery and Climate Experiment (GRACE)[J]. Water Resources Research, 37(5):1327-1339. |
| [47] | Rodell M, Famiglietti J S. 2002. The potential for satellite-based monitoring of groundwater storage changes using GRACE:the High Plains aquifer, Central US[J]. Journal of Hydrology, 2002, 263(1-4):245-256. |
| [48] | Rodell M, Famiglietti J S, Chen J, et al. 2004b. Basin scale estimates of evapotranspiration using GRACE and other observations[J]. Geophysical Research Letters, 31(20):L20504. |
| [49] | Rodell M, Houser P R, Jambor U, et al. 2004a. The Global land data assimilation system[J]. Bulletin of the American Meteorological Society, 85(3):381-394. |
| [50] | Rodell M, Velicogna I, Famiglietti J S. 2009. Satellite-based estimates of groundwater depletion in India[J]. Nature, 460(7258):999-1002. |
| [51] | Rowlands D D, Luthcke S B, Klosko S M, et al. 2005. Resolving mass flux at high spatial and temporal resolution using GRACE intersatellite measurements[J]. Geophysical Research Letters, 32(4):L04310. |
| [52] | Sasgen I, Martinec Z, Fleming K. 2006. Wiener optimal filtering of GRACE data[J]. Studia Geophysica et Geodaetica, 50(4):499-508. |
| [53] | Schmidt R, Schwintzer P, Flechtner F, et al. 2006. GRACE observations of changes in continental water storage[J]. Global and Planetary Change, 50(1-2):112-126. |
| [54] | Schmidt R, Petrovic S, Güntner A, et al. 2008. Periodic components of water storage changes from GRACE and global hydrology models[J]. Journal of Geophysical Research:Solid Earth (1978-2012), 113(B8):B08419. |
| [55] | Seo K W, Wilson C R, Famiglietti J S, et al. 2006. Terrestrial water mass load changes from Gravity Recovery and Climate Experiment (GRACE)[J]. Water Resources Research, 42(5):W05417. |
| [56] | Strassberg G, Scanlon B R, Rodell M. 2007. Comparison of seasonal terrestrial water storage variations from GRACE with groundwater-level measurements from the High Plains Aquifer (USA)[J]. Geophysical Research Letters, 34(14):L14402. |
| [57] | Swenson S, Famiglietti J, Basara J, et al. 2008. Estimating profile soil moisture and groundwater variations using GRACE and Oklahoma Mesonet soil moisture data[J]. Water Resources Research, 44(1):W01413. |
| [58] | Swenson S, Wahr J. 2002. Methods for inferring regional surface-mass anomalies from Gravity Recovery and Climate Experiment (GRACE) measurements of time-variable gravity[J]. Journal of Geophysical Research:Solid Earth (1978-2012), 107(B9):ETG 3-1-ETG 3-13. |
| [59] | Swenson S, Wahr J, Milly P C D. 2003. Estimated accuracies of regional water storage variations inferred from the Gravity Recovery and Climate Experiment (GRACE)[J]. Water Resources Research, 39(8):1223. |
| [60] | Swenson S, Wahr J. 2006a. Post-processing removal of correlated errors in GRACE data[J]. Geophysical Research Letters, 33(8):L08402. |
| [61] | Swenson S, Wahr J. 2006b. Estimating large-scale precipitation minus evapotranspiration from GRACE satellite gravity measurements[J]. Journal of Hydrometeorology, 7(2):252-270. |
| [62] | Swenson S, Yeh P J F, Wahr J, et al. 2006. A comparison of terrestrial water storage variations from GRACE with in situ measurements from Illinois[J]. Geophysical Research Letters, 33(16):L16401. |
| [63] | Syed T H, Famiglietti J S, Chambers D P. 2009. GRACE-based estimates of terrestrial freshwater discharge from basin to continental scales[J]. Journal of Hydrometeorology, 10(1):22-40. |
| [64] | Syed T H, Famiglietti J S, Rodell M, et al. 2008. Analysis of terrestrial water storage changes from GRACE and GLDAS[J]. Water Resources Research, 44(2):W02433. |
| [65] | Tapley B D, Bettadpur S, Ries J C, et al. 2004a. GRACE measurements of mass variability in the Earth system[J]. Science, 305(5683):503-505. |
| [66] | Tapley B D, Bettadpur S, Watkins M, et al. 2004b. The gravity recovery and climate experiment:Mission overview and early results[J]. Geophysical Research Letters, 31(9):L09607. |
| [67] | Tiwari V M, Wahr J, Swenson S. 2009. Dwindling groundwater resources in northern India, from satellite gravity observations[J]. Geophysical Research Letters, 36(18):L18401. |
| [68] | Velicogna I, Wahr J. 2005. Greenland mass balance from GRACE[J]. Geophysical Research Letters, 32(18):L18505. |
| [69] | Velicogna I, Wahr J. 2006. Measurements of time-variable gravity show mass loss in Antarctica[J]. Science, 311(5768):1754-1756. |
| [70] | Voss K A, Famiglietti J S, Lo M H, et al. 2013. Groundwater depletion in the Middle East from GRACE with implications for transboundary water management in the Tigris-Euphrates-Western Iran region[J]. Water Resources Research, 49(2):904-914. |
| [71] | Wahr J, Molenaar M, Bryan F. 1998. Time variability of the Earth's gravity field:Hydrological and oceanic effects and their possible detection using GRACE[J]. Journal of Geophysical Research:Solid Earth (1978-2012), 103(B12):30205-30229. |
| [72] | Wahr J, Swenson S, Zlotnicki V, et al. 2004. Time-variable gravity from GRACE:First results[J]. Geophysical Research Letters, 31(11):L11501. |
| [73] | Wahr J, Swenson S, Velicogna I. 2006. Accuracy of GRACE mass estimates[J]. Geophysical Research Letters, 33(6):L06401. |
| [74] | Wang X W, de Linage C, Famiglietti J, et al. 2011. Gravity Recovery and Climate Experiment (GRACE) detection of water storage changes in the Three Gorges Reservoir of China and comparison with in situ measurements[J]. Water Resources Research, 47(12):W12502. |
| [75] | Wang W X, Shi Y L, Gu G H, et al. 2010. Gravity changes associated with the Ms8.0 Wenchuan earthquake detected by GRACE[J]. Chinese Journal of Geophysics (in Chinese), 53(8):1767-1777, doi:10.3969/j.issn.0001-5733.2010.08.002. |
| [76] | Wang H S, Wang Z Y, Yuan X D, et al. 2007. Water storage changes in Three Gorges water systems area inferred from GRACE time-variable gravity data[J]. Chinese Journal of Geophysics (in Chinese), 50(3):730-736, doi:10.3321/j.issn:0001-5733.2007.03.011. |
| [77] | Wang H S, Wu P, Xu H Z. 2009. A review of research in glacial isostatic adjustment[J]. Progress in Geophysics (in Chinese), 24(6):1958-1967, doi:10.3969/j.issn.1004-2903.2009.06.005. |
| [78] | Wang Z T, Li J C, Jiang W P, et al. 2008. Determination of earth gravity field model WHU-GM-05 using GRACE gravity data[J]. Chinese Journal of Geophysics (in Chinese), 51(5):1364-1371, doi:10.3321/j.issn:0001-5733.2008.05.010. |
| [79] | Werth S, Güntner A, Schmidt R, et al. 2009. Evaluation of GRACE filter tools from a hydrological perspective[J]. Geophysical Journal International, 179(3):1499-1515. |
| [80] | Wiener N. 1964. Extrapolation, Interpolation, and Smoothing of Stationary Time Series[M]. Cambridge, MA:MIT Press. |
| [81] | Winsemius H C, Savenije H H G, van de Giesen N C, et al. 2006. Assessment of Gravity Recovery and Climate Experiment (GRACE) temporal signature over the upper Zambezi[J]. Water Resources Research, 42(12):W12201. |
| [82] | Wouters B, Schrama E J O. 2007. Improved accuracy of GRACE gravity solutions through empirical orthogonal function filtering of spherical harmonics[J]. Geophysical Research Letters, 34(23):L23711. |
| [83] | Xing L L, Li H, Xuan S B, et al. 2012. Long-term gravity changes in Chinese mainland from GRACE and terrestrial gravity measurements[J]. Chinese Journal of Geophysics (in Chinese), 55(5):1557-1564, doi:10.6038/j.issn.0001-5733.2012.05.013. |
| [84] | Yamamoto K, Fukuda Y, Nakaegawa T, et al. 2007. Landwater variation in four major river basins of the Indochina peninsula as revealed by GRACE[J]. Earth, Planets, and Space, 59(4):193-200. |
| [85] | Yang Y D, E D C, Zhao D B, et al. 2009. Seasonal and inter-annual change in land water storage from GRACE[J]. Chinese Journal of Geophysics (in Chinese), 52(12):2987-2992, doi:10.3969/j.issn.0001-5733.2009.12.007. |
| [86] | Yeh P J F, Famiglietti J S. 2008. Regional terrestrial water storage change and evapotranspiration from terrestrial and atmospheric water balance computations[J]. Journal of Geophysical Research:Atmospheres (1984-2012), 113(D9):D09108. |
| [87] | Yeh P J F, Swenson S C, Famiglietti J S, et al. 2006. Remote sensing of groundwater storage changes in Illinois using the Gravity Recovery and Climate Experiment (GRACE)[J]. Water Resources Research, 42(12):W12203. |
| [88] | Zaitchik B F, Rodell M, Reichle R H. 2008. Assimilation of GRACE terrestrial water storage data into a land surface model:Results for the Mississippi River basin[J]. Journal of Hydrometeorology, 9(3):535-548. |
| [89] | Zhang Z Z, Chao B F, Lu Y, et al. 2009. An effective filtering for GRACE time-variable gravity:Fan filter[J]. Geophys. Res. Lett., 36(17):L17311. |
| [90] | Zheng W, Xu H Z, Zhong M, et al. 2009. Effective processing of measured data from GRACE key payloads and accurate determination of Earth's gravitational field[J]. Chinese Journal of Geophysics (in Chinese), 52(8):1966-1975, doi:10.3969/j.issn.0001-5733.2009.08.003. |
| [91] | Zhou X H, Wu B, Peng B B, et al. 2006. Detection of global water storage variation using GRACE[J]. Chinese Journal of Geophysics (in Chinese), 49(6):1644-1650, doi:10.3321/j.issn:0001-5733.2006.06.010. |
| [92] | 曹艳萍,南卓铜. 2011. GRACE重力卫星数据的水文应用综述[J].遥感技术与应用, 26(5):543-553. |
| [93] | 翟宁,王泽民,伍岳等. 2009.利用GRACE反演长江流域水储量变化[J].武汉大学学报·信息科学版, 34(4):436-439. |
| [94] | 段建宾,钟敏,闫昊明等. 2007.利用重力卫星观测资料解算中国大陆水储量变化[J].大地测量与地球动力学, 27(3):68-71. |
| [95] | 鄂栋臣,杨元德,晁定波. 2009.基于GRACE资料研究南极冰盖消减对海平面的影响[J].地球物理学报, 52(9):2222-2228, doi:10.3969/j.issn.0001-5733.2009.09.005. |
| [96] | 胡小工,陈剑利,周永宏等. 2006.利用GRACE空间重力测量监测长江流域水储量的季节性变化[J].中国科学D辑:地球科学, 36(3):225-232. |
| [97] | 金涛勇,李建成,王正涛等. 2010.近四年全球海水质量变化及其时空特征分析[J].地球物理学报, 53(1):49-56, doi:10.3969/j.issn.0001-5733.2010.01.006. |
| [98] | 鞠晓蕾,沈云中,张子占. 2013.基于GRACE卫星RL05数据的南极冰盖质量变化分析[J].地球物理学报, 56(9):2918-2927, doi:10.6038/cjg20130906. |
| [99] | 李琼,罗志才,钟波等. 2013.利用GRACE时变重力场探测2010年中国西南干旱陆地水储量变化[J].地球物理学报, 56(6):1843-1849, doi:10.6038/cjg20130606. |
| [100] | 廖海华,钟敏,周旭华. 2010.利用GRACE卫星重力资料解算气候驱动的地表周年垂直形变[J].地球物理学报, 53(5):1091-1098, doi:10.3969/j.issn.0001-5733.2010.05.009. |
| [101] | 罗志才,李琼,钟波. 2012.利用GRACE时变重力场反演黑河流域水储量变化[J].测绘学报, 41(5):676-681. |
| [102] | 苏晓莉,平劲松,黄倩等. 2009.重力卫星检测到的全球陆地水储量变化[J].中国科学院上海天文台年刊, (30):14-21. |
| [103] | 苏晓莉,平劲松,叶其欣. 2012. GRACE卫星重力观测揭示华北地区陆地水量变化[J].中国科学:地球科学, 42(6):917-922. |
| [104] | 汪汉胜,王志勇,袁旭东等. 2007.基于GRACE时变重力场的三峡水库补给水系水储量变化[J].地球物理学报, 50(3):730-736, doi:10.3321/j.issn:0001-5733.2007.03.011. |
| [105] | 汪汉胜, Wu P,许厚泽. 2009.冰川均衡调整(GIA)的研究[J].地球物理学进展, 24(6):1958-1967, doi:10.3969/j.issn.1004-2903.2009.06.005. |
| [106] | 王武星,石耀霖,顾国华等. 2010. GRACE卫星观测到的与汶川Ms8.0地震有关的重力变化[J].地球物理学报, 53(8):1767-1777, doi:10.3969/j.issn.0001-5733.2010.08.002. |
| [107] | 王正涛,李建成,姜卫平等. 2008.基于GRACE卫星重力数据确定地球重力场模型WHU-GM-05[J].地球物理学报, 51(5):1364-1371, doi:10.3321/j.issn:0001-5733.2008.05.010. |
| [108] | 邢乐林,李辉,刘东至等. 2007.利用GRACE时变重力场监测中国及其周边地区的水储量月变化[J].大地测量与地球动力学, 27(4):62-65. |
| [109] | 邢乐林,李辉,玄松柏等. 2012. GRACE和地面重力测量监测到的中国大陆长期重力变化[J].地球物理学报, 55(5):1557-1564, doi:10.6038/j.issn.0001-5733.2012.05.013. |
| [110] | 许民,叶柏生,赵求东. 2013. 2002-2010年长江流域GRACE水储量时空变化特征[J].地理科学进展, 32(1):68-77. |
| [111] | 许朋琨,张万昌. 2013. GRACE反演近年青藏高原及雅鲁藏布江流域陆地水储量变化[J].水资源与水工程学报, 24(1):23-29. |
| [112] | 杨元德,鄂栋臣,晁定波等. 2009. GRACE估算陆地水储量季节和年际变化[J].地球物理学报, 52(12):2987-2992, doi:10.3969/j.issn.0001-5733.2009.12.007. |
| [113] | 叶叔华,苏晓莉,平劲松等. 2011.基于GRACE卫星测量得到的中国及其周边地区陆地水量变化[J].吉林大学学报(地球科学版), 41(5):1580-1586. |
| [114] | 郑伟,许厚泽,钟敏等. 2009. GRACE卫星关键载荷实测数据的有效处理和地球重力场的精确解算[J].地球物理学报, 52(8):1966-1975, doi:10.3969/j.issn.0001-5733.2009.08.003. |
| [115] | 钟敏,段建宾,许厚泽等. 2009.利用卫星重力观测研究近5年中国陆地水量中长空间尺度的变化趋势[J].科学通报, 54(9):1290-1294. |
| [116] | 周旭华,吴斌,彭碧波等. 2006.全球水储量变化的GRACE卫星检测[J].地球物理学报, 49(6):1644-1650, doi:10.3321/j.issn:0001-5733.2006.06.010. |
| [117] | 朱广彬,李建成,文汉江等. 2008.利用GRACE时变重力位模型研究全球陆地水储量变化[J].大地测量与地球动力学, 28(5):39-44. |
| [118] | 周江存,孙和平,徐建桥. 2009.用地表和空间重力测量验证全球水储量变化模型[J].科学通报, 54(9):1282-1289. |
| [119] | 邹正波,邢乐林,李辉等. 2008.中国大陆及邻区GRACE卫星重力变化研究[J].大地测量与地球动力学, 28(1):23-27. |
 2015, Vol. 30
2015, Vol. 30

