2015, Vol. 30
2. 武汉大学中国南极测绘研究中心, 武汉 430079
2. Chinese Antarctic Center of Surveying and Mapping, Wuhan University, Wuhan University, Wuhan 430079, China
在卫星精密定轨和重力场解算等相关卫星大地测量问题的研究中，引力位及其一、二阶导数有着重要的应用(Montenbruck and Gill，2000; Vallado，2001)，例如，引力位非球形部分的一阶导数是卫星受到的主要摄动力，二阶导数是精密定轨中求解状态转移矩阵的重要组成部分.关于引力位及其一、二阶导数的计算，国内外学者进行过大量的研究.传统Legendre方法计算速度和精度取决于缔合Legendre函数及其一、二阶导数的计算，故以往研究多集中于缔合Legendre函数及其导数的递推方法及去奇异研究上(Holmes and Featherstone，2002; Jekeli et al.，2007;刘晓刚等，2010)，并在超高阶次缔合勒让德函数计算方法上取得较多成果(张传定等，2004；彭富清，2004；吴星和刘雁雨，2006；王建强等，2009；刘缵武等，2011；Fukushima，2012；于锦海等，2015)，但传统Legendre方法存在球坐标和直角坐标之间的转换，无法克服在极点计算的奇异性(Casotto and Fantino，2007).Lundberg和Schutz(1988)使用新的变量及Helmholtz多项式，消除了奇异性，即Pines方法(Pines，1973; Balmino et al.，1990).Cunningham(1970)使用引力位的复数表达形式，推导了引力位及其任意阶导数的直角坐标递推计算公式，但其表达式比较复杂，Lin(1997)基于Cunningham方法，提出一种改进的快速计算方法，并运用于卫星定轨中.Sünkel(2002)和钟波(2010)给出了Cunningham正规化的递推公式，表达式相对简洁，易于程序实现.张传定和吴晓平(2003)基于Belikov(1991)递推方法引入新的球函数定义，给出一套简洁的公式，极大的提高了计算效率.Fantino和Casotto(2009)对广泛使用的4种方法重新推导整理，即传统Legendre方法，基于Clenshaw求和的变量方法，Pines方法和Cunningham-Metris方法，从计算精度和效率方面进行了比较，但其对传统Legendre方法中的Legendre函数及其导数的递推并未采用最佳的方法.上述方法均是从显示表达式出发的，而引力位的一、二阶导数的计算还可以采用数值微分方法，无需复杂的显示表达式.Abad和Lacruz(2013)提出一种新的基于自动微分的方法，可以计算引力位的任意阶次的导数，并且易于实现并行化，可极大的提高计算效率.
本文综合已有成果，选择了其中的3种较优方法进行比较研究：即传统Legendre方法，Cunningham直角坐标递推方法，张传定和吴晓平(2003)提出的方法(下称Zhang方法).有关引力位及其一、二阶导数的计算公式比较繁琐，已有文献存在一些细节错误，这些细微的错误对高精度计算会产生影响.为此，本文首先对3种方法的公式进行重新推导整理，给出上述3种方法较为准确的计算公式，并使用GRAIL(Gravity Recovery and Interior Laboratory)(Roncoli and Fujii，2010)卫星在科学任务阶段轨道数据以及最新660阶次月球重力场模型GRGM660PRIM(Zuber et al.，2013; Lemoine et al.，2013)，从计算精度和效率角度对3种方法进行分析比较，最后给出相关计算建议.
1 引力位及其一、二阶导数计算公式引力位可表示为(Heiskanen and Moritz，1979)
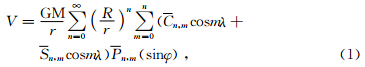
该方法先求位函数V对(r，λ，φ)的偏导数，然后根据(r，λ，φ)与(x，y，z)的函数关系求得(r，λ，φ)对(x，y，z)的偏导数，进一步根据链式法则得到V对(x，y，z)的偏导数，用同样的思路可以求得V的二阶导数.该方法思路简明，计算速度和精度主要取决于正规化缔合Legendre函数Pn，m(μ)及其一、二阶导数的递推.下面分别给出V的一、二阶导数的计算公式：
V的一阶导数，即引力矢量，可表示为
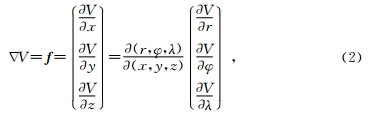
V的二阶导数，即引力梯度张量，可表示为
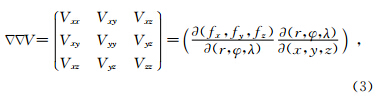
式(2)(3)中的偏导数具体表达式见钟波(2010)及附录.由偏导数具体表达式可以看出，V的一、二阶导数的计算涉及到缔合Legendre函数及其一、二阶导数的计算.综合苏勇等(2012)，于锦海和万晓云(2010)，于锦海等(2015)和刘晓刚(2011)的研究结果，本文采用计算速度和稳定性较好的跨阶次递推方法计算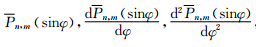
，详细递推公式见苏勇等(2012).递推公式中用到相同的系数αnm，βnm，γnm，在实际程序设计中，这些与位置无关的系数可先进行计算，存储到内存，从而减少运算量.
Cunningham(1970)通过引入新的组合形式，对式(1)进行变形，得出引力位V及其一、二阶导数的直角坐标递推关系，从而消除了球坐标和直角坐标相互转换带来的奇异性，但此递推关系是基于自然形式的Legendre函数的组合得到的.Sünkel(2000)给出正规化Cunningham递推方法，其递推公式形式简单，易于编程实现，但其公式部分系数有误，本文重新推导整理，给出公式为
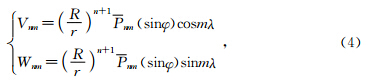
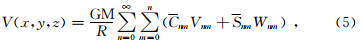
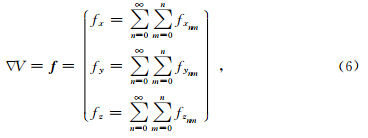
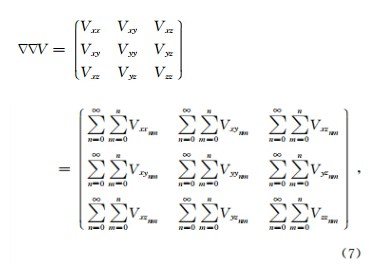
在研究Legendre函数递推问题上，Belikov(1991)引入了新的非正常化球谐函数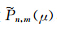
，给出一组递归公式，递推公式乘系数绝对值小于1，提高了递推的稳定性.张传定和吴晓平(2003)基于Belikov引入的非正常化球谐函数，结合调和函数的性质，给出V及其一、二阶导数的递推公式，使得计算效率有显著提高.其思路是先定义非正常化球谐函数
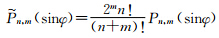，则式(1)用非正常化球谐函数可表示为
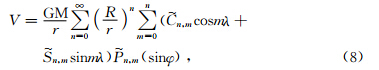
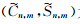为非正常化引力位系数.
引力位V的一阶导数可表示为
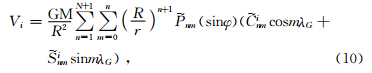
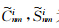为递推系数，N为引力场截断的最高阶次.n从1开始取值，相应的，非球形部分n从3开始取值.
按照式(10)的逻辑关系，可以写出引力位V的二阶导数，即▽▽V各分量为
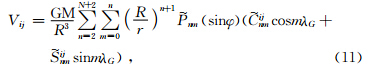
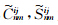为递推系数.n从2开始取值，非球形部分n从4开始取值.式(8)～(11)的计算涉及到
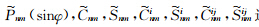递推，具体公式见附录说明.
2 数值实验及其分析
为比较上述3种方法的计算效率和精度，本文使用GRAIL-A(Gravity Recovery and Interior Laboratory)在科学任务阶段(2012-03-01T10:00:00 至 2012-05-29T18:00:00)获取的轨道数据(采样点257279个，纬度覆盖范围为-89.9108981393°至89.8469351768°)，基于660阶次重力场模型GRGM660PRIM，分别计算了V，▽V，▽▽V.
本文采用Fortran90实现上述3种方法，数据类型使用real×8，采用相同的输入输出接口，对于与位置无关的递推系数，例如αnm，βnm，γnm，(A5)(A6)等，在调用3种方法前统一计算并存储到内存，从而减少重复计算.本文实验平台是IVF 11.0.3451，Intel(R)Core(TM)i7-3630QM CPU @ 2.40 GHz 四核，8.00 GB，Window 8，64 bit.
2.1 计算效率比较
对于以上257279个采样点，分别计算了3对组合V，V+▽V和V+▽V+▽▽V，并统计其CPU耗时(表 1).图 1为三种方法耗时的对比图.从表 1可以看出，在仅计算引力位V时，Zhang方法虽然优于前2种方法，但不明显；在计算V+ ▽V时，Legendre方法效率明显高于Cunningham方法，原因在于Legendre方法采用了跨阶次方法，计算二阶导数时，递推式中用到相同的系数αnm，βnm，γnm，减少了运算量.Zhang方法此时体现出一定的优越性，原因为计算▽V项时，公式(10)仍然使用非正常化的球谐函数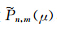，无需新的递推，且形式比较统一，可极大的减少了运算量；对于V+▽V+▽▽V的计算，Zhang方法的计算速度是Legendre方法的1.3倍，Cunningham方法的2.3倍，表现出最高的效率.为进一步提高计算效率，可以充分利用▽▽V的对角线满足拉普拉斯方程的性质，只需计算其中2个分量即可.
|
表 1 3种方法的计算时间(s)和奇异性 Table 1 CPU time(s) and singularity of the three methods |
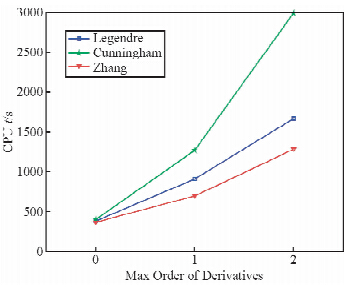 | 图 1 3种方法的CPU耗时比较 Fig. 1 CPU Times of the three methods |
由于目前关于引力位V及其一、二阶导数并没有一个“真值”，本文采用相对精度RP(Relative Precision)对3种方法进行比较，计算公式(Holmes and Featherstone，2002)为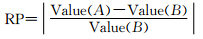
，式中Value(A)，Value(B)分别表示A，B方法计算的结果，本文以计算效率较高的Zhang方法为基准，分别计算了Legendre方法和Cunningham方法的相对精度.图 2，图 3分别为两种方法计算V，▽V的相对精度.图 4为对角线分量满足Laplace方程的精度，表 2为其统计结果.
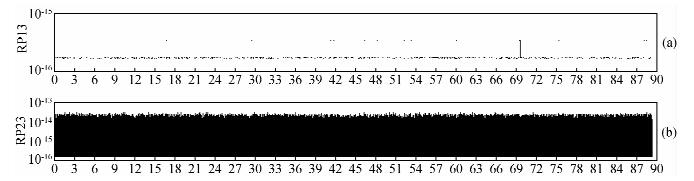 | 图 2 V的相对精度，(a)是Legendre方法的相对精度，(b)是Cunningham方法的相对精度 Fig. 2 The relative precision of V，(a) figure shows RP from the Legendre method, (b) shows RP from the Cunningham method |
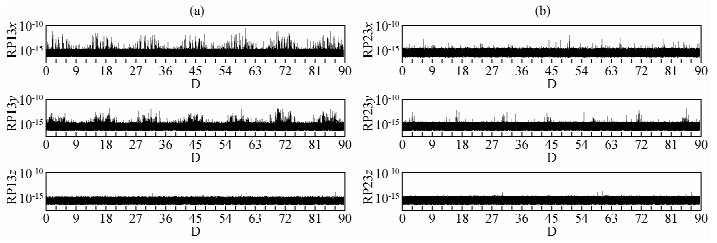 | 图 3 ▽V的相对精度，(a)是Legendre方法的相对精度，(b)是Cunningham方法的相对精度 Fig. 3 The relative precision of ▽V，(a)shows ▽V RP from the Legendre method, (b) shows ▽V RP from the Cunningham method |
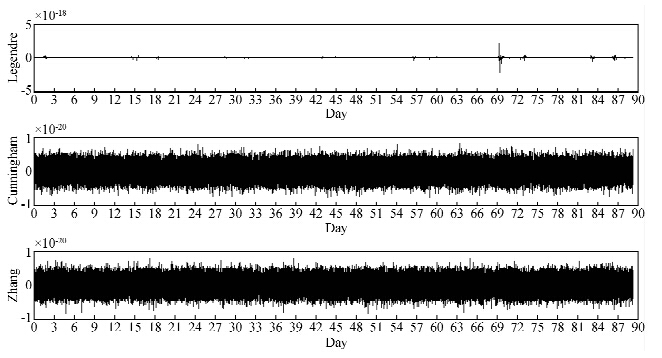 | 图 4 ▽▽V对角线分量满足Laplace方程的精度 Fig. 4 The Laplacian accuracy of ▽▽V |
|
|
表 2 ▽▽V对角线分量满足Laplace方程精度的统计结果 Table 2 The statistical result of ▽▽V Laplacian accuracy |
由图 2可以看出，在计算V时，Cunningham方法的相对精度为10-16～10-14，稳定性低于Legendre方法.原因在于：Cunningham方法计算V的精度取决于Vnm，Wnm的递推精度，Vnm，Wnm的递推实质是列递推，随着阶次的升高会积累误差；而Legendre方法中缔合Legendre函数的计算采用了跨阶次递推方法，稳定性较好.
关于▽V的精度，由图 3可以看出，Cunningham方法的相对精度比Legendre方法略高，且Legendre方法稳定性明显不如Cunningham方法.原因在于GRAIL卫星为极轨卫星，当卫星进入极区时，计算纬度接近90°，此时Pn，m(μ)及其一阶导数的计算精度下降，并且式(A1)中的分母含有cosφ项，两者会最终导致Legendre方法计算▽V的精度下降.综合图 2和图 3分析，Zhang方法和Legendre方法计算V的精度相当，均优于Cunningham方法，计算▽V时，Zhang方法仍然使用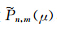，并且不存在球坐标和直角坐标之间的转换，稳定性较好，计算精度和Cunningham方法相当，均为10-16～10-14.
图 4，表 2反映▽▽V的对角线符合Laplace方程的精度，3种方法均能以10-21的精度满足Laplace方程，其中Zhang方法精度最高，为1.553E-021.与Cunningham方法和Zhang方法相比，Legendre方法的精度相对较差.同上分析，式(A1)～(A2)中Jacob矩阵的分母含cosφ，且随着纬度接近90°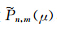，及其一、二阶导数的计算精度下降，从而致使Legendre方法计算▽▽V的精度下降，这也是Legendre方法计算 ▽V，▽▽V的固有缺点.
本文讨论了三种计算引力位及其一、二阶导数的方法，即传统Legendre方法，Cunningham直角坐标递推方法和Zhang方法，使用GRAIL卫星轨道数据，采用660阶次月球重力场模型GRGM660PRIM，从计算效率和精度角度进行了对比分析，得出以下结论：
(1)本文给出了3种方法的计算公式，修正Cunningham方法递推公式部分系数和Zhang方法中引力位V的一、二阶导数表达式，并经过实际数值对比验证，表明本文的公式较为准确.
(2)由于Cunningham直角坐标递推方法采用列递推求VnmWnm，计算引力位V时稳定性不如Legendre和Zhang方法，且需要大量的递推计算，计算效率也不如Legendre和Zhang方法.
(3)通过3种方法的比较，发现Zhang方法无论从计算效率还是编程易实现性上都明显优于前2种方法，是对Fantino和Casotto(2009)中提到的4种方法的一种重要补充.
(4)传统Legendre方法存在奇异，在实际数据处理时，当纬度接近90°时，可采用其他非奇异的方法，例如本文提到的其他两种方法替代以确保计算精度.
致 谢 感谢审稿专家及编辑部的支持. 附录：相关递推公式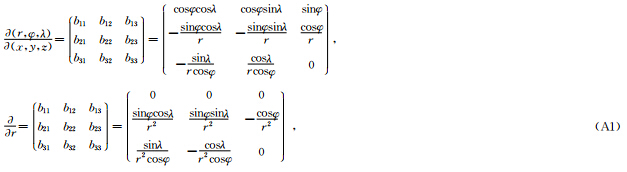 
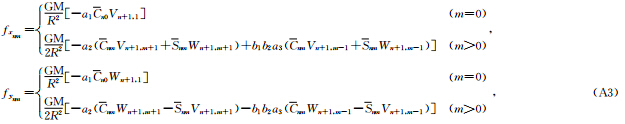
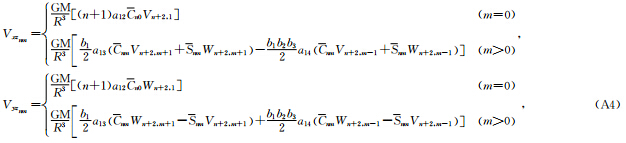
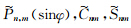递推公式详见张传定和吴晓平(2003)，下面给出
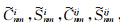易于程序实现的递推公式为
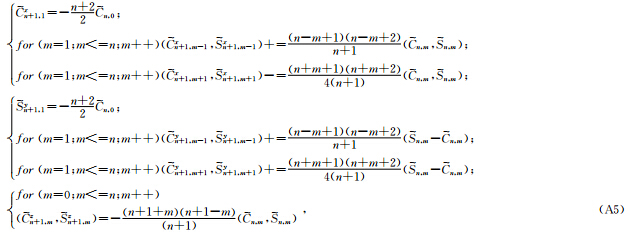
| [1] | Abad A, Lacruz E. 2013. Computing derivatives of a gravity potential by using automatic differentiation[J]. Celestial Mechanics and Dynamical Astronomy, 117(2):187-200. |
| [2] | Balmino G, Barriot J P, Valès N. 1990. Non-singular formulation of the gravity vector and gravity gradient tensor in spherical harmonics[J]. Manuscr. Geod., 15(1):11-16. |
| [3] | Belikov M V. 1991. Spherical harmonic analysis and synthesis with the use of column-wise recurrence relations[J]. Manuscr. Geod., 16(6):384-410. |
| [4] | Casotto S, Fantino E. 2007. Evaluation of methods for spherical harmonic synthesis of the gravitational potential and its gradients[J]. Advances in Space Research, 40(1):69-75. |
| [5] | Cunningham L E. 1970. On the computation of the spherical harmonic terms needed during the numerical integration of the orbital motion of an artificial satellite[J]. Celestial Mechanics, 2(2):207-216. |
| [6] | Fantino E, Casotto S. 2009. Methods of harmonic synthesis for global geopotential models and their first-, second-and third-order gradients[J]. Journal of Geodesy, 83(7):595-619. |
| [7] | Fukushima T. 2012. Numerical computation of spherical harmonics of arbitrary degree and order by extending exponent of floating point numbers[J]. Journal of Geodesy, 86(4):271-285. |
| [8] | Heiskanen W A, Moritz H. 1979. Physical Geodesy (in Chinese)[M]. Beijing:Surveying and Mapping Press. |
| [9] | Holmes S A, Featherstone W E. 2002. A unified approach to the Clenshaw summation and the recursive computation of very high degree and order normalised associated legendre functions[J]. Journal of Geodesy, 76(5):279-299. |
| [10] | Jekeli C, Lee J K, Kwon J H. 2007. On the computation and approximation of ultra-high-degree spherical harmonic series[J]. Journal of Geodesy, 81(9):603-615. |
| [11] | Lemoine F G, Goossens S, Sabaka T J, et al. 2013. High? degree gravity models from GRAIL primary mission data[J]. Journal of Geophysical Research:Planets, 118(8):1676-1698. |
| [12] | Lin Q C. 1997. Fast computation of the spherical harmonic perturbation on an artificial satellite[J]. Science in China Series E:Technological Sciences, 40(3):324-330. |
| [13] | Liu X G. 2011. Theory and methods of the earth's gravity field model recovery from GOCE data (in Chinese)[Ph. D. thesis]. Zhengzhou:PLA Information Engineering University. |
| [14] | Liu X G, Wu X P, Zhao D M, et al. 2010. Non-singular expression of the disturbing gravity gradients[J]. Acta Geodaetica et Cartographica Sinica (in Chinese), 39(5):450-457. |
| [15] | Liu Z W, Liu S H, Huang O, et al. 2011. Scale factors in recursion of ultra-high degree and order Legendre functions and Horner's scheme of summation[J]. Acta Geodaetica et Cartographica Sinica (in Chinese), 40(4):454-458. |
| [16] | Lundberg J B, Schutz B E. 1988. Recursion formulas of legendre functions for use with nonsingular geopotential models[J]. Journal of Guidance, Control, and Dynamics, 11(1):31-38. |
| [17] | Montenbruck O, Gill E. 2000. Satellite Orbits:Models, Methods, and Applications[M]. Berlin Heidelberg:Springer. |
| [18] | Peng F Q. 2004. Algorithms for computing ultra-high-degree disturbing geopotential elements[J]. Chinese J. Geophys.(in Chinese), 47(6):1023-1-28. |
| [19] | Pines S. 1973. Uniform representation of the gravitational potential and its derivatives[J]. AIAA Journal, 11(11):1508-1511. |
| [20] | Roncoli R B, Fujii K K. 2010. Mission design overview for the gravity recovery and interior laboratory (GRAIL) mission[C].//AIAA/AAS Astrodynamics Specialist Conference, 2010-8383. |
| [21] | Sünkel H. 2002. From E? tv? s to mGal Final report[R]. ESA/ESTEC Contract 13392/NL/GD. |
| [22] | Su Y, Fan D M, You W. 2012. Fast and stably recursive algorithm for computing second derivative of associated legendre functions[J]. Geomatics and Information Science of Wuhan University (in Chinese), 37(12):1409-1412. |
| [23] | Vallado D A. 2001. Fundamentals of Astrodynamics and Applications[M]. 2nd ed. Dordrecht:Kluwer Academic Publishers. |
| [24] | Wang J G, Zhao G Q, Zhu G B. 2009. Contrastive analysis of common computing methods of ultra-high degree and order fully normalized associated Legendre function[J]. J. Geod. Geodyn.(in Chinese), 29(2):126-130. |
| [25] | Wu X, Liu Y Y. 2006. Comparison of computing methods of the ultra-high degree and order[J]. Journal of Zhengzhou Institute of Surveying and Mapping (in Chinese), 23(3):188-191. |
| [26] | Yu J H, Wan X Y. 2010. Non-singular Formulae for Computing Derivatives of Legendre Functions[J]. Journal of Geomatics Science and Technology (in Chinese), 27(1):1-3. |
| [27] | Yu J H, Zeng Y Y, Zhu Y C, et al. 2015. A recursion arithmetic formula for Legendre functions of ultra-high degree and order on every other degree[J]. Chinese J. Geophys. (in Chinese), 58(3):748-755, doi:10.6038/cjg20150305. |
| [28] | Zhang C D, Wu X P. 2003. Fast computation method of non-central perturbation force[J]. Geomatics and Information Science of Wuhan University (in Chinese), 28(S):87-90. |
| [29] | Zhang C D, Xu H Z, Wu X. 2004. Typros problem in harmonic analysis of the gravity field (in Chinese)[C].//Proc. Geod. and Geodyn. Hubei:Science and Technology Press, 302-314. |
| [30] | Zhong B. 2010. Study on the Determination of the earth's gravity field from satellite gravimetry mission GOCE (in Chinese)[Ph. D. thesis]. Wuhan:Wuhan University. |
| [31] | Zuber M T, Smith D E, Watkins M M, et al. 2013. Gravity field of the moon from the gravity recovery and interior laboratory (GRAIL) mission[J]. Science, 339(6120):668-671. |
| [32] | Heiskanen W A, Moritz H. 1979.物理大地测量学[M].卢福康,胡国理,译.北京:测绘出版社. |
| [33] | 刘晓刚. 2011. GOCE卫星测量恢复地球重力场模型的理论与方法[博士论文].郑州:解放军信息工程大学. |
| [34] | 刘晓刚,吴晓平,赵东明,等. 2010.扰动重力梯度的非奇异表示[J].测绘学报, 39(5):450-457. |
| [35] | 刘缵武,刘世晗,黄欧,等. 2011.超高阶次勒让德函数递推计算中的压缩因子和Horner求和技术[J].测绘学报, 40(4):454-458. |
| [36] | 彭富清. 2004.超高阶扰动场元的计算方法[J].地球物理学报, 47(6):1023-1028. |
| [37] | 苏勇,范东明,游为. 2012.缔合Legendre函数二阶导数的快速稳定递推算法[J].武汉大学学报·信息科学版, 37(12):1409-1412. |
| [38] | 王建强,赵国强,朱广彬. 2009.常用超高阶次缔合勒让德函数计算方法对比分析[J].大地测量与地球动力学, 29(2):126-130. |
| [39] | 吴星,刘雁雨. 2006.多种超高阶次缔合勒让德函数计算方法的比较[J].测绘科学技术学报, 23(3):188-191. |
| [40] | 于锦海,万晓云. 2010.计算Legendre函数导数的非奇异方法[J].测绘科学技术学报, 27(1):1-3. |
| [41] | 于锦海,曾艳艳,朱永超,等. 2015.超高阶次Legendre函数的跨阶数递推算法[J].地球物理学报, 58(3):748-755, doi:10.6038/cjg20150305. |
| [42] | 张传定,吴晓平. 2003.非心摄动引力的快速计算方法研究[J].武汉大学学报·信息科学版, 28(S):87-90. |
| [43] | 张传定,许厚泽,吴星. 2004.地球重力场调和分析中的"轮胎"问题[C].//《大地测量与地球动力学进展》论文集.湖北:科学技术出版社, 302-314. |
| [44] | 钟波. 2010.基于GOCE卫星重力测量技术确定地球重力场的研究[博士论文].武汉:武汉大学. |