2. 中国地震局地震预测研究所, 北京 100036
2. Institute of Earthquake Science, China Earthquake Administration, Beijing 10036, China
中国大陆地处印度-欧亚板块碰撞引起的复杂变形区内,地震活动频发.统计表明,全球约有33%的大陆地震发生在中国境内(Zhang et al.,2003).随着社会经济的不断发展和城市化进程的不断加剧,出现了越来越多的人口高密区域.因此,分析中国大陆的地震危险性具有非常重要的意义.
随着GPS(Global Positioning System)等空间大地测量技术的发展,研究中国大陆的变形特征已经有很多研究成果(Jiang and Ma.,2003; Calais et al.,2006; 郑文俊等,2009).但是,前人研究局限于对形变场模型反映的研究区域变形特征的分析,在前人的研究结果中,变形较大的区域存在应变积累,也即为潜在的震源区.然而,GPS数据得到的形变场模型包含瞬时变形、断层蠕滑等非震形变、由已发地震释放的永久形变和震间弹性变形.因此,用大地测量资料分析研究区域的地震危险性,需要扣除已发地震产生的永久形变及其它非震形变.
Holt等(1995)利用历史地震资料反演了中、东亚的速度场;任金卫等(1999,2002)和Holt等(2000)利用地震资料、GPS等大地测量资料和第四纪活断层资料联合反演了中国大陆及其邻区的应变率场和速度场.上述模型分别从运动学和动力学的角度实际客观地描述了中国大陆及其邻区现今变形特征,为进一步分析该区域的地震危险性提供了基础资料.
本文在任金卫等(2002)的研究基础上,详细搜集整理了1900-2013年间发生在中国大陆及其邻区的4级及其以上历史地震资料,并对其中47个地表破裂带较长(40 km)的大震做了分段.其次,利用历史地震资料、第四纪活断层资料和GPS等大地测量资料联合反演了研究区域的应变率场和速度场.最后,利用历史地震资料和反演的应变率场估算了研究区域的地震矩亏损,为分析研究区域的地震危险性提供参考资料.
1 估算中国大陆及其邻区的剩余应变率和地震矩率 1.1 历史地震资料搜集和整理首先搜集了1900-2013年间发生在中国大陆及其邻区的1349个4级及其以上历史地震资料(图 1),震源球大小用矩震级(MW)表示.其中,1976-2013年间的地震资料来自哈佛大学全球地震中心矩张量目录(CMT);1964-1976年的历史地震资料通过总结前人的研究成果得到(Chen et al.,1977; Molnar et al.,1983,1984; Holt et al.,1991a);1900-1964的地震资料主要来自于Molnar等(1984)和Anne等(1984)的研究成果.图 1中,1900-2013年间,中国东北、蒙古东部和华南地区地震较少.
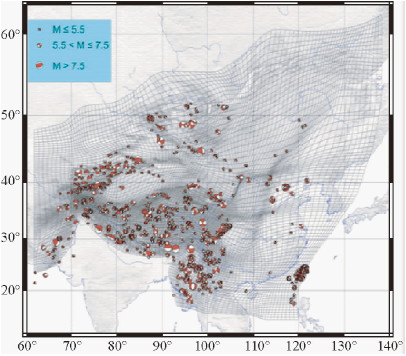 | 图 1 中国大陆及其邻区地震震源机制 Fig. 1 Focal mechanisms of Chinese mainland and its vicinity |
任金卫等(2002)将中国大陆及其邻区划分成不规则的地质构造单元,并结合地震资料、GPS等大地测量资料和第四纪活断层资料,反演了研究区域现今应变率场和速度场.为了减小大震的影响范围和提高反演结果的空间分辨率,本文对网格进行加密,从原来的12×11个增加到96×88个不规则的四边形网格.利用改进的双三次样条方法(Haines et al.,1993; Beaven et al.,2001)反演了中国大陆及其邻区的应变率场( mod,图 2),并利用
mod,图 2),并利用 mod估算了模型矩率(
mod估算了模型矩率( 0mod)(Haines et al.,1993; Beaven et al.,2001)为
0mod)(Haines et al.,1993; Beaven et al.,2001)为

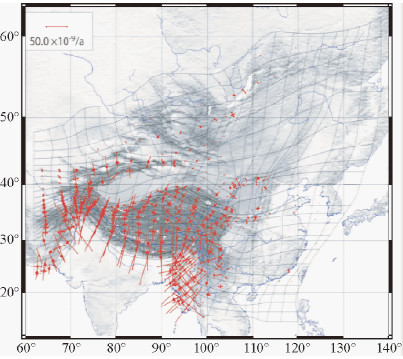 | 图 2 利用地震资料、第四纪活断层资料和GPS资料联合反演的研究区域的应变率场(单位:10-9/a),图例表示50×10-9/a的拉张应变率 Fig. 2 Strain rate model determined from earthquake data,Quaternary fault rates and GPS observations (units:10-9/a),Legend is 50×10-9/a of tensional strain rate |
 φφ,
φφ, θθ,
θθ, φθ为
φθ为 mod的分量,φ为东向,θ为北向;μ为剪切模量,取3.0×1011dyne.cm-2;V为网格的面积乘以孕震厚度(15 km(Holt et al.,1995)).需要指出的是,反演资料中增加了Liang等(2013)的GPS观测结果和荆燕等(2004)总结的活断层资料;反演使用的网格如图 1所示,成图时通过加权平均法估算了较大尺度网格的应变率(图 2)和对应的地震矩率.
mod的分量,φ为东向,θ为北向;μ为剪切模量,取3.0×1011dyne.cm-2;V为网格的面积乘以孕震厚度(15 km(Holt et al.,1995)).需要指出的是,反演资料中增加了Liang等(2013)的GPS观测结果和荆燕等(2004)总结的活断层资料;反演使用的网格如图 1所示,成图时通过加权平均法估算了较大尺度网格的应变率(图 2)和对应的地震矩率.
利用Kostrov求和公式(Molnar et al.,1984; Kostrov.,1974)(式2)和历史地震资料(图 1)估算各网格的应变率观测值( obs)为
obs)为


利用式1和 obs估算各网格的观测矩率(
obs估算各网格的观测矩率( 0obs),则剩余矩率Δ
0obs),则剩余矩率Δ 0=
0= 0mod-
0mod- 0obs.各网格的剩余应变率张量Δ
0obs.各网格的剩余应变率张量Δ =
= mod-
mod- obs(图 3a),再利用Δ
obs(图 3a),再利用Δ 求地震震源参数(式4~11)(Shentu et al.,1998),则可将Δ
求地震震源参数(式4~11)(Shentu et al.,1998),则可将Δ 0用震源球表示(图 3b).图 3(a,b)中,红色表示地震矩率亏损,即Δ
0用震源球表示(图 3b).图 3(a,b)中,红色表示地震矩率亏损,即Δ 0>0;蓝色为地震矩率盈余,即Δ
0>0;蓝色为地震矩率盈余,即Δ 0 < 0.断层面走向(θ),倾角(δ),滑动角(λ)表示为
0 < 0.断层面走向(θ),倾角(δ),滑动角(λ)表示为
 其中,
其中,

 φφ、Δ
φφ、Δ θθ和Δ
θθ和Δ φθ为Δ
φθ为Δ 的分量.
的分量.
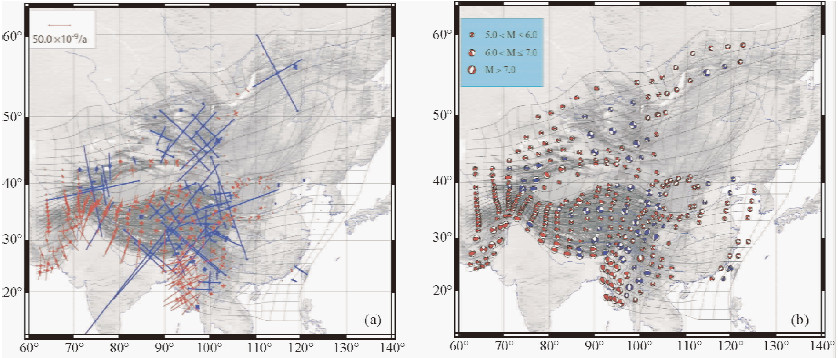 |
图 3 (a)剩余应变率,模型应变率( mod)和应变率观测值( mod)和应变率观测值( obs)之差. 红色为Δ obs)之差. 红色为Δ 0>0,蓝色为Δ 0>0,蓝色为Δ 0<0,图例表示50×10-9/a的拉张应变率. (b)剩余地震矩率.其中,红色表示地震矩率亏损(Δ 0<0,图例表示50×10-9/a的拉张应变率. (b)剩余地震矩率.其中,红色表示地震矩率亏损(Δ 0>0); 蓝色表示地震矩率盈余(Δ 0>0); 蓝色表示地震矩率盈余(Δ 0 < 0)
Fig. 3 (a) Residual strain rate from the difference between predicted strain rate ( 0 < 0)
Fig. 3 (a) Residual strain rate from the difference between predicted strain rate ( mod) and strain rate observations ( mod) and strain rate observations ( obs),in which red represents Δ obs),in which red represents Δ 0>0 and blue represents Δ 0>0 and blue represents Δ 0 < 0.Legend is 50×10-9/a of tensional strain rate. (b) Residual moment rate,in which red represents moment rate deficit (Δ 0 < 0.Legend is 50×10-9/a of tensional strain rate. (b) Residual moment rate,in which red represents moment rate deficit (Δ 0>0) and blue represents moment rate surplus (Δ 0>0) and blue represents moment rate surplus (Δ 0 < 0) 0 < 0)
|
图 3中的应变率和地震矩率盈余量(蓝色)分布很不合理,主要表现在喜马拉雅逆冲断裂带,东昆仑断裂、海原断裂带和蒙古高原等有大震发生的地区.在喜马拉雅逆冲断裂带,1934年比哈尔-尼泊尔地震的发震断裂为近E-W的逆冲断裂,其地表破裂长度达到200 km以上(Singh and Harsh,1980),然而,图 3所示的盈余量主要分布在震中和其北边的网格,并未按照地震产生的形变带分布.昆仑山口西地震的发震断裂长度达到420 km(Lin et al.,2002),破裂长度至少横穿三个网格,破裂带东段所在的网格却存在较大的地震矩率和应变率亏损.上述不合理性存在的主要原因是估算剩余应变率和地震矩率时,将大震以点源的形式释放,使大震形变分布过于集中而并未按照其破裂带分布,从而使存在大震的网格应变率观测值出现峰值.
2 7级及其以上大震的分段处理和研究区域的地震矩亏损 2.1 7级及其以上大震的分段处理为了解决2.2中存在的问题,本文将历史地震分为两类:第一类包括所有小于7级和7级以上但地表破裂带较短(40 km,接近于本文网格尺度)的地震;第二类为47个7级及其以上且地表破裂带较长的地震.详细搜集整理了第二类地震的震源参数、地表破裂带和地表位移资料(表 1).根据资料的完整程度将其分成A,B,C三类:A类,震源参数完整且有地表位移观测资料;B类,震源参数相对完整,存在发震断裂和地表破裂带资料,但缺少地表位移观测数据;C类,缺少发震断裂和地表破裂带资料.
|
|
表 1 1900-2013年间中国大陆及其邻区7级及其以上地震资料总结 Table 1 Summary of materials about 47 earthquakes with magnitude greater than or equal to 7.0 in Chinese Mainland and its vicinity between 1900-2013 |
对A类地震,首先根据地表破裂带展布和本文网格之间的位置关系将破裂带分段,再根据地表位移分布估算各子破裂段的地震矩和矩震级.对缺少地表位移观测资料的B类地震,由于地震地表位移总体呈现中间大、两边小的分布特征,在此假定其服从三角形分布(Martin and Beroza,2000),利用与A类地震相同的分段方法将其分段.C类地震缺少地表位移和破裂带资料,首先,利用经验公式(Wesnousky,2008)估算破裂带长度,假定震源位于破裂带中间,根据走向参数和震源位置确定地表破裂带位置,再利用B类地震的方法分段.地震分段时,由于各破裂子段长度已知,通过调整破裂矩形面宽度,使分段后子地震的地震矩之和与该地震的地震矩观测值保持一致,47个大震的分段结果见图 4.
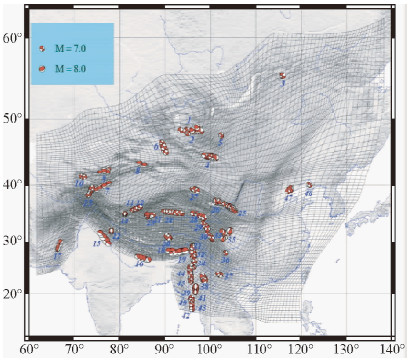 | 图 4 47个大震子地震的震源机制 Fig. 4 Focal mechanisms of sub earthquakes of 47 major events |
将所有第一类地震和分段处理的第二类地震利用Kostrov求和公式估算各网格的应变率观测值( obs),再根据(2.2)的方法估算各网格的剩余应变率(Δ
obs),再根据(2.2)的方法估算各网格的剩余应变率(Δ )和剩余地震矩率(Δ
)和剩余地震矩率(Δ ).为了使表述更为清晰,将Δ
).为了使表述更为清晰,将Δ 转化成与地震矩率相关的应变率Δ
转化成与地震矩率相关的应变率Δ (式12),如图 5a所示.其中,红色表示地震矩率亏损(即Δ
(式12),如图 5a所示.其中,红色表示地震矩率亏损(即Δ 0>0),蓝色表示地震矩率盈余(即Δ
0>0),蓝色表示地震矩率盈余(即Δ 0 < 0),公式(11)为
0 < 0),公式(11)为

 φφ,Δ
φφ,Δ θθ,Δ
θθ,Δ φθ为Δ
φθ为Δ 的分量,再利用式(13)估算各网格的地震矩为
的分量,再利用式(13)估算各网格的地震矩为 
 | 图 5 (a)中国大陆及其邻区的剩余应变率(扣除蠕动等非震形变);(b)由图5a的剩余应变率估算的地震矩亏损(红色)和盈余(蓝色) Fig. 5 (a)Residual strain rate of Chinese Mainland and its vicinity (Part of aseismic deformation is removed);(b)Moment deficit (red) and surplus (blue) evaluated from residual strain rate in figure 5a |
图 5a中,应变率亏损较大的区域主要包括喜马拉雅断裂带、天山、阿尔金断裂带、青藏高原中南部、川滇地区、鄂尔多斯块体周缘和东南沿海等区域.在鄂尔多斯块体内部,塔里木盆地,华南块体和中国东北的亏损量相对较小,与该区域较低的构造活动特征(张培震等,2013)一致.图 5b为利用剩余应变率估算的研究区域113年间的地震矩亏损(红色)和盈余(蓝色),其中的地震震源机制反映了相关区域的力学性质,震源球由矩震级大小确定.表 2为研究区域主要活动块体和断裂的地震矩亏损量及对应的矩震级.
|
|
 2015, Vol. 30
2015, Vol. 30


