地球物理学进展  2015, Vol. 30 Issue (6): 2482-2488   PDF    
引用本文
雷伟伟, 张捍卫. 2015. 地球扁率对天体引潮力影响的计算与分析[J]. 地球物理学进展, 30(6): 2482-2488, doi: 10.6038/pg20150606  
LEI Wei-wei, ZHANG Han-wei. 2015. The calculation and analysis of effect of earth's flattening on tidal generating force of celestial bodies. Progress in Geophysics, 30(6): 2482-2488, doi: 10.6038/pg20150606   
地球扁率对天体引潮力影响的计算与分析
雷伟伟, 张捍卫    
河南理工大学测绘与国土信息工程学院, 焦作 454000
收稿日期: 2015-08-18 修回日期: 2015-10-10.
基金项目: 国家自然科学基金(41474021:精密引潮力位展开与地球自转速率潮汐变化研究)资助.
作者简介: 雷伟伟,男,1982年生,博士生,讲师,主要从事大地测量学教学与科研工作.(E-mail:geodesy@163.com)
摘要: 高精度天体引潮力计算中需要考虑地球扁率的影响.由DE421历表计算得到太阳系各个天体在GCRS中的坐标,基于天球参考系经典的岁差章动转换方法、IERS 2010规范推荐的转换参数以及IERS发布的EOP 08 C04数据模型,在综合考虑影响天体坐标转换的各种因素(框架偏差、岁差、章动、地球自转、时间尺度转换、极移)改正后,得到天体在ITRS中的坐标,并由此计算得到1962年至2015年间地球扁率对各天体引潮力位和引潮力影响的具体数值.计算结果表明:地球扁率对天体引潮力的影响,对月球来说不超过1.8898×10-11 ms-2(1.8898 nGal),对太阳来说不超过0.0018×10-11 ms-2(0.0018 nGal),对其他天体来说可完全忽略不计.地球扁率对月球、太阳引潮力影响的变化周期与相应天体的运行周期一致.
关键词: 地心天球参考系(GCRS)     国际地球参考系(ITRS)     IERS 2010规范     岁差章动模型     DE421历表    
The calculation and analysis of effect of earth's flattening on tidal generating force of celestial bodies
LEI Wei-wei, ZHANG Han-wei    
School of Geodesy & Land Information Engineering, Henan Polytechnic University, Jiaozuo 454000, China
Abstract: The effect of earth's flattening must be considered when calculating the high-precision tidal generating force of celestial bodies. In this paper, the coordinates of celestial bodies of solar system in GCRS were calculated based on DE421, these coordinates were transformed to ITRS through celestial reference system equinox-based precession-nutation transformation method, parameters recommended by IERS Conventions (2010) and the EOP 08 C04 model provided by IERS, including celestial reference frame bias, precession, nutation, earth rotation, the difference between TT and UT1, polar motion, et al. The numerical values of tidal generating potential and tidal generating force are calculated based on the basic formulas. The results indicate that between 1962 and 2015 the earth's flattening effect on moon's tidal generating force doesn't exceed 1.8898×10-11 ms-2(1.8898 nGal), and that effect on sun doesn't exceed 0.0018×10-11 ms-2(0.0018 nGal), and that effect on other celestial bodies can completely be neglected. The results also indicated that the period of effect of the tidal generating force by moon and sun was consistent with the corresponding celestial bodies' period.
Key words: geocentric celestial reference system     international terrestrial reference system     IERS conventions 2010     precession-nutation model     DE421 ephemeris    
0 引 言

精密引潮力位及引潮力的计算是地球物理学、大地测量学和空间科学研究的基本理论问题，它不仅可以提高空间测地技术的归算精度(测站位移和地球重力场的精确计算、地球自转速率变化的准确预测等)，而且对地球内部物理结构和动力学演化、板块运动和地壳形变监测等科学研究均具有重要意义，同时还可应用精密引潮力位展开建立刚体地球章动序列(张捍卫，2005).郗钦文(1999)和张捍卫(2010)分别指出，地球扁率对引潮力的影响不超过5×10-11 ms-2(5 nGal，1 nGal=1×10-11 ms-2)，这在高精度的潮汐分析、引潮力计算中是必须要考虑的.其实Bartels早在1957年就曾指出这一问题，随后Wilhelm(1983)和Dahlen(1993)给出了相关的计算公式，但使用的数学工具太过于专门化；Hartmann和Wenzel(1995a)在此基础上，通过对公式中参数的数量级估计，表明当引潮力位计算截断阈值为0.001×10-11 ms-2(0.001 nGal)时，需要考虑地球扁率对月球和太阳引潮力的影响，对其他行星的影响则不需考虑；郝洪涛(2010)基于ELP2000-85月球历表估算得到地球扁率对月球引潮力的影响在2×10-11 ms-2(2 nGal)以内.在理论公式改进推导方面，郗钦文(1999)基于位理论和微积分中求原函数的方法，推导出地球扁率对引潮位的影响公式；张捍卫(2010)则通过对地球质心处受力分析，利用坐标转换方法，导出了顾及地球扁率的引潮位表达式.刘复刚(2013)基于行星会合指数运动学方程，分析了行星系统对太阳的引潮力的变化特征与规律.

上述影响数值均为根据理论公式估算得到的结果，而其具体数值目前尚没有明确的研究成果，本文基于IERS 2010规范推荐的DE421历表，根据地球扁率对天体引潮力影响的理论公式和天球参考系经典的岁差章动转换模型，在综合考虑影响天体坐标转换的各种因素(框架偏差、岁差、章动、地球自转、时间尺度转换、极移)改正后，计算了地球扁率对各个天体引潮力影响的具体数值.本文成果不但为引潮力位展开截断项的选择提供理论依据，同时也能为实际的潮汐数据分析提供取舍依据.

1 理论公式

在历元t地球扁率对天体引潮位的影响Vf(t)为(郗钦文，1999；张捍卫，2010)：

(1)式中，t为从J2000.0起算的TT(法Temps Terrestre/英Terrestrial Time，地球时)儒略世纪数；GM为天体的万有引力与质量之积；(λ，φ，r)、(α，δ，R)分别为如图 1所示的测站点、天体在ITRS(International Terrestrial Reference System，国际地球参考系)中的地心经度、地心纬度、地心距；a、J2⊕分别为地球椭球半长轴、地球重力场二阶带球谐系数，IERS 2010规范(Petit and Luzum，2010)中对二者的推荐值分别为a=6378136.6 m、J2⊕=1.0826359×10-3.另外，Pmn(x)为n阶m次完全规格化缔合勒让德函数，其中x∈[-1，1]，n、m均为0或正整数，且n≥m，在本文中用到：

由此，就可得Vf在ITRS中球坐标系下的径向、经向、纬向梯度gS，rf、gS，λf、gS，φf分别为

记测站在ITRS中的椭球大地坐标为(L，B，H)，则有：

式中，N、e分别为地球椭球的卯酉圈曲率半径、第一偏心率.

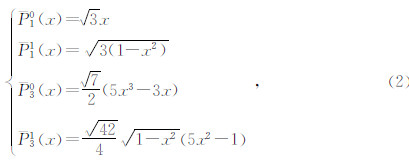
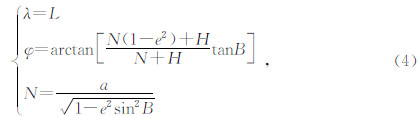
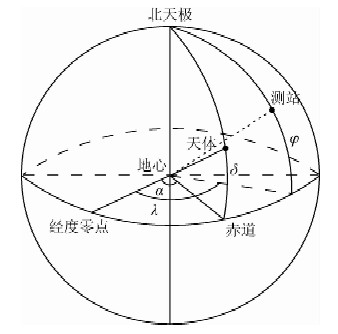图 1 天体、测站在地心天球中的位置 Fig. 1 The position of celestrial body and station in the geocentric celestial sphere

由于重力仪测量数据是基于铅垂线方向，故需将(3)式中基于球坐标系的径向元素转换为基于铅垂线方向的元素.Wenzel(1974，1995b)指出此处可忽略垂线偏差的影响，只需将基于球面的径向元素转换为基于椭球面的法向元素即可.记Δφ为测站点处的大地纬度B与球心纬度φ之差(即径向与法向的夹角)，则ITRS中球坐标系下以径向为基准的gS，rf、gS，λf、gS，φf还需要转换为ITRS中以椭球法线为基准的gE，rf、gE，Lf、gE，Bf，转换公式为

gE，rf即为地球扁率对天体引潮力的影响.gE，Lf、gE，Bf分别为地球扁率对引潮位的法向经度、纬度梯度值的影响，是计算地倾斜固体潮和天文经、纬度固体潮的基础(郭俊义，2001).

2 天体坐标计算与转换

从(1)式中可以看出，计算天体坐标(α，δ，R)是引潮位Vf计算的基础，在天体测量中，天体坐标是基于天体历表计算得到的，目前应用最为广泛天体历表的是由美国NASA(National Aeronautics and Space Administration，美国航空航天局)的JPL(Jet Propulsion Laboratory，喷气推进实验室)发布的DE系列历表(Development Ephemeris，展开历表)，是基于数值积分方法获得的数值历表.

IERS 2010规范将DE421历表作为ICRS(International Celestial Reference System，国际天球参考系)的动力学实现并推荐使用(Petit & Luzum，2010)，因此，在本文中天体坐标(α，δ，R)是基于DE421历表计算得到的.由DE421历表计算得到的是天体在GCRS(Geocentric Celestial Reference System，地心天球参考系)中的坐标，还需要将其转换为ITRS中的坐标.

2.1 时间尺度

在天体测量中出于不同目的采用不同的时间尺度，其中DE系列历表中的时间尺度为TDB(法Temps Dynamique Barycentrique /英Barycentric Dynamical Time，质心力学时)，而ITRS、岁差模型、章动模型、飞行器轨道计算中的运动积分等的时间尺度均为TT，TDB与TT之间差值的大小不超过±1.7 ms(millisecond，毫秒)，此差值在太阳系动力学历表计算中可忽略不计(李广宇，2010，2015；Soffel & Langhans，2013)，在本文接下来的计算过程中，时间尺度均采用TT.

2.2 DE421历表计算

DE421历表包含1个头文件“header.421”、2个数据文件“ascp1900.421、ascp2050.421”和1个测试位置文件“testpo.421”，时间范围从1899年12月4日至2200年2月1日，其中在头文件中给出了228个天文常数数据，两个数据文件中共有3426个数据块，每个数据块中包含32天的数据.

采用JPL发布的Fortran程序进行计算，首先将两个Ascii格式的数据文件进行合并，接下来通过子程序“asc2eph.f”将其转换为二进制格式的数据文件，然后通过“testeph.f”子程序以及测试位置文件数据验证数据格式转换是否有误，当确保转换无误后，最后根据子程序“PLEPH”进行所需天体坐标的计算.在计算过程中，中心星为地球，目标星分别为各个待计算天体，时间尺度为地球时TT，计算得到各天体在GCRS中的三维直角坐标.

DE421历表数据及计算程序可从ftp://ssd.jpl.nasa.gov/pub/eph/planets下载，其中头文件、数据文件以及测试位置文件等历表数据在ascii文件夹中，各个子程序在fortran文件夹中.

2.3 GCRS到ITRS转换的数学模型

在历元t，由GCRS到ITRS经典的基于春分点的岁差章动转换方法的数学模型为(Petit and Luzum，2010)：

式中[ITRS]、[GCRS] 分别表示相应参考系下的三维直角坐标，Q eqx(t)、 R eqx(t)、 W(t)分别称为框架偏差-岁差-章动矩阵、地球自转矩阵、极移矩阵，三个矩阵的计算模型分别为

在框架偏差-岁差-章动矩阵 Q eqx(t)中，B 为参考框架偏差矩阵(简称框架偏差)，P为岁差矩阵，N 为章动矩阵，它们的计算公式分别为

岁差矩阵 P还有另一种表示方法为

对于(9)式，Capitaine(2003)、Fukushima(2003)指出，在接近J2000.0时，zA和ζA对参考架偏差矩阵 B 非常敏感，从而导致它们不能用多项式表达，转换精度大大降低，所以应该避免使用这种岁差转换方法.而(8)式中的岁差矩阵 P 将赤道岁差和黄道岁差非常清晰地区分开，且意义明确，Capitaine(2003)建议在进行岁差转换时，应该采用(8)中的岁差矩阵 P .

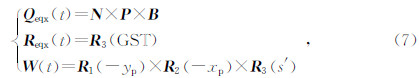
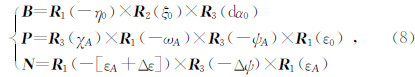
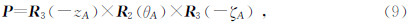
在岁差矩阵 P和章动矩阵N 中，ψA、ωA为基本赤道岁差参数，χA为黄道岁差导出量，εA为瞬时黄赤交角，ζA、θA、zA为赤道岁差参考导出量，Δψ为黄经章动，Δε为交角章动，这些岁差-章动元素如图 2所示，它们的具体数值是基于岁差-章动模型计算得到的.

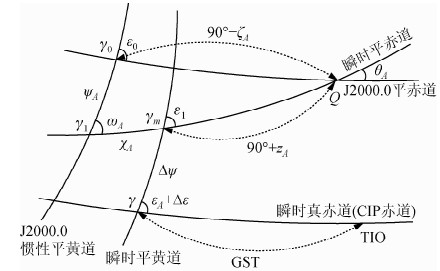图 2 岁差章动参数 Fig. 2 The parameters of precession and nutation

在地球自转矩阵 R eqx(t)中，GST(Greenwich Sidereal Time)为格林尼治真恒星时，可根据格林尼治平恒星时GMST(Greenwich Mean Sidereal Time)、赤经章动EE(Equation of the Equinoxes)以及赤经章动补充项EECT(Complementary Terms of the Equation of the Equinoxes)计算得到：

在极移矩阵 W(t)中，xp、yp是CIP(Celestial Intermediate Pole，天球中间极)在ITRS中极移的两个分量，s′为TIO(Terrestrial Intermediate Origin，地球中间零点)定位角，表示TIO在CIP赤道上的位置，它们的计算公式为

式中等号右端三项分别表示IERS数据中心发布的极移数据、由海洋潮汐引起的极移量、由章动引起的极移量，得到公式为

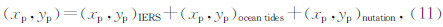
上述基于春分点的坐标转换过程见图 3所示.

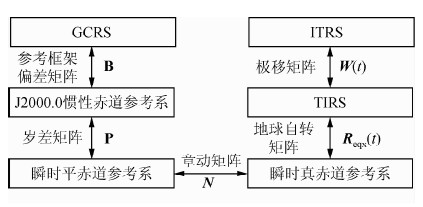图 3 坐标转换过程示意图 Fig. 3 The flowchart of transformation between GCRS and ITRS

图 2中在GCRS与ITRS转换过程中涉及到四个中间参考系，它们的基本情况列于表 1中.

表 1 四个中间参考系的基本情况 Table 1 The datum of four intermediate reference systems
2.4 GCRS到ITRS转换参数的计算

在由GCRS到ITRS转换的数学模型中，涉及到众多转换参数，对这些转换参数的计算概述如下(Petit & Luzum，2010；刘佳成，2012).

参考架偏差是由于在标准历元J2000.0时刻岁差-章动模型给出的天极、分点与GCRS的天极、经度零点不重合造成的.ξ0、η0表示CIP在GCRS中J2000.0时刻的天极偏差，其值由VLBI观测得出，dα0为瞬时平春分点的赤经偏差值，其值由LLR观测资料分析得到.框架偏差矩阵 B 中参数的数值分别为

岁差矩阵 P 中参数的计算采用IERS 2010规范推荐的IAU 2006岁差模型为

章动矩阵 N 中参数的计算采用IERS 2010规范推荐的IAU 2000AR06章动模型为

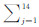其中ARGUMENT=kjFj.限于篇幅，模型具体内容请参考IERS 2010规范5.6节，这里不再详细说明.模型中具体数据可从ftp://tai.bipm.org/iers/conv2010/chapter5或ftp://toshi.nofs.navy.mil/conv2010/chapter5下载获取，计算黄经章动Δψ所需的数据在tab5.3a.txt文件中，计算交角章动Δε所需的数据在tab5.3b.txt文件中.

根据IERS 2010规范的推荐，地球自转矩阵中各相关参数计算模型为

在(17)中计算地球自转角ERA时，Tu为从J2000.0起算的儒略日数，时间尺度为UT1(Universal Time，世界时).这就涉及到地球时TT与世界时UT1之间的转换，记二者的差值为ΔT=TT-UT1.

雷伟伟(2015)根据USNO(United States Navy Observatory，美国海军天文台)发布的三个ΔT数据文件，基于最小二乘法拟合得到一组新的计算ΔT的六次多项式经验公式，不仅适用于公元纪年、JD、MJD以及从J2000.0起算的儒略世纪数等四种时间格式，便于程序设计，而且精度远高于目前国际上常用的Morrison和Stephenson经验公式(李广宇，2010)的结果，故而在本文中予以采用.

在赤经章动EE计算公式中，Δψ、εA分别为IAU 2000AR06章动模型、IAU 2006岁差模型的计算结果.赤经章动补充项EECT模型数据可以从ftp://tai.bipm.org/iers/conv2010/chapter5/ tab5.2e.txt或ftp://toshi.nofs.navy.mil/conv2010/chapter5/ tab5.2e.txt下载获取.

(xp，yp)IERS是由IERS数据中心发布的EOP(Earth Orientation Parameters，地球定向参数)模型数据中的一部分，本文采用最新发布的EOP 08 C04模型，该模型为每天一组不断更新的数据，且数据延迟一个月，模型数据可从http://datacenter.iers.org/eop/-/somos/ 5Rgv/latest/214下载.

IERS 2010 规范推荐(xp，yp)ocean tides、(xp，yp)nutation的计算模型分别为

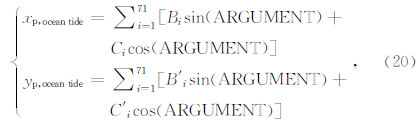
两式中ARGUMENT=∑j=16kjFj，两个模型的具体数据分别由IERS 2010规范中表 8.2和表 5.1给出，文中不再列出.

s′由IERS2010规范推荐计算公式为

3 计算与分析

在由GCRS到ITRS的转换过程中，需要知道极移量xp、yp，但由于地球自转的不规则性和不可预知性，极移数据无法准确预测，因此只能根据已发布的相关数据进行实验计算.目前，IERS数据处理中心发布的地球长期自转数据模型EOP 08 C04中，提供了从1962年1月1日至今的每天一组的极移数据.

基于DE421历表、GCRS到ITRS的转换模型、EOP 08 C04模型以及(1~6)式，本文计算了从1962年1月1日至2015年3月1日之间每隔1小时Vf、gE，rf、gE，Lf、gE，Bf的具体数值.为了更加全面地研究地球扁率对各个天体引潮力的影响大小，本文选择月球、太阳、水星、金星、火星、木星、土星、天王星、海王星、冥王星10个天体进行计算，各天体的GM值采用DE421历表头文件“header.421”中给出的数值.

Wenzel(1995a，1995b)、Roosbeek(1996)、Kudryavtsev(2004)在进行引潮力计算或引潮位展开研究时，均以德国Black Forest Observation(BFO)测站为例进行计算，为了与国际研究保持一致，本文也以该测站位置为例进行计算.BFO 测站的椭球大地坐标为B=48.330600°N、L=8.3300°E、 H=589 m，根据(4)式可得到其地心坐标为φ=48.139419°、λ=8.3300°、r=6366836.969 m.

计算步骤为：

(1)首先由DE421历表计算各天体在GCRS中的三维直角坐标，根据(6)式转换得到各天体在ITRS中的三维直角坐标，然后计算出ITRS中的地心坐标(α，δ，R)；基于(1~3)式计算得到地球扁率对各个天体引潮位、引潮力的影响Vf、gS，rf、gS，λf、gS，φf，最后由(5)式转换得到gE，rf、gE，Lf、gE，Bf.

(2)计算Vf的截断阈值选取为10-8 m2s-2，计算gE，rf、gE，Lf、gE，Bf的截断阈值选取为0.0001×10-11 ms-2(0.0001 nGal)，各个天体相关计算结果的统计值列于表 2中.

从表 2中可以看出，地球扁率对月球的引潮位、引潮力等的影响最大，对太阳引潮位、引潮力等的影响次之，对其他天体引潮位、引潮力等的影响可完全忽略不计.因此，在进行高精度引潮力计算时，当计算截断阈值为1×10-11 ms-2(1 nGal)时，仅需考虑地球扁率对月球的影响；当计算截断阈值为0.001×10-11 ms-2(0.001 nGal)时，需要考虑地球扁率对月球、太阳的影响.

表 2 地球扁率对各个天体的影响统计表(1962.1.1-2015.3.1) Table 2 Statistics of each planet influenced by earth’s flattening (1962.1.1-2015.3.1)

计算结果表明地球扁率对月球、太阳引潮力的影响的最大数值分别为1.8898×10-11 ms-2(1.8898 nGal)和0.0018×10-11 ms-2(0.0018 nGal)，这个结果验证了郗钦文(1999)、张捍卫(2010)、Hartmann & Wenzel(1995a)、郝洪涛(2010)论文中关于地球扁率对月球、太阳引潮力影响的数值估计量级的正确性，并且表明郝洪涛(2010)估计的数值最为准确.

为了更加直观地分析地球扁率对月球、太阳引潮力的影响，在图 4中给出了2014年9月1日至2015年3月1日之间6个月内月球的gE，rf、gE，Lf、gE，Bf数值变化图；在图 5中给出了2010年1月1日至2015年1月1日之间5年内太阳的gE，rf、gE，Lf、gE，Bf数值变化图.

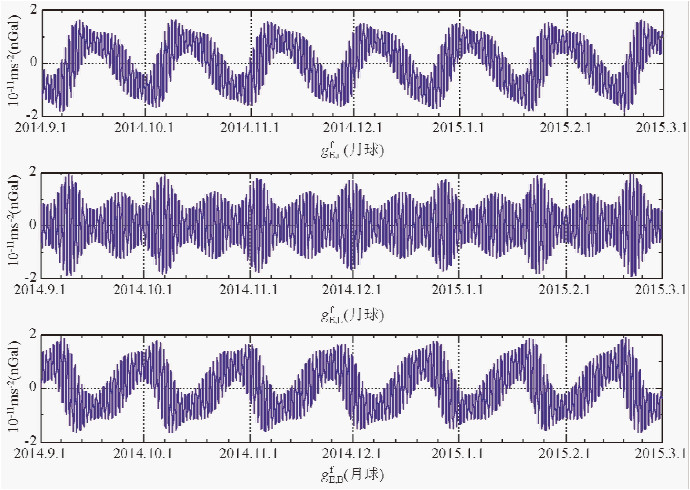图 4 月球gE,rf、gE,Lf、gE,Bf变化图(2014.9.1-2015.3.1) Fig. 4 The numerical distribution of moon’s gE,rf、gE,Lf、gE,Bf(2014.9.1-2015.3.1)

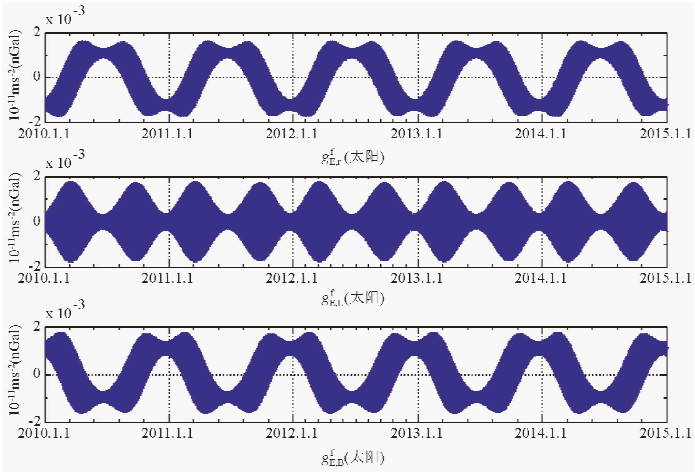图 5 太阳gE,rf、gE,Lf、gE,Bf变化图(2010.1.1-2015.1.1) Fig. 5 The numerical distribution of sun’s gE,rf、gE,Lf、gE,Bf(2010.1.1-2015.1.1)

从图 4中可以看出，月球的

gE，rf、gE，Lf、gE，Bf

数值变化具有很明显的周期性，大约28天一个周期，这个周期和月球绕地运动的周期是一致的，说明地球扁率对月球引潮位、引潮力等的影响和月球的运动是密切相关的.同样，在图 5中，太阳

gE，rf、gE，Lf、gE，Bf

的数值变化是以1年为周期，这和地球的公转周期也是一致的.

4 结论

本文从地球扁率对天体引潮位影响的理论公式出发，基于DE421历表计算得到天体在GCRS中的坐标，根据IERS 2010规范推荐的天球参考系转换模型得到天体在ITRS中的坐标，计算了1962年至2015年间地球扁率对月球、太阳、水星、金星、火星、木星、土星、天王星、海王星、冥王星10个天体引潮位和引潮力影响的具体数值.计算结果表明地球扁率对月球、太阳引潮力影响的最大值分别为1.8898×10-11 ms-2(1.8898 nGal)和0.0018×10-11 ms-2(0.0018 nGal)，对其他天体引潮力的影响可以完全忽略不计.同时表明地球扁率对月球、太阳引潮力的影响具有很强的周期性，且周期与月球绕地运行周期、地球公转周期一致.

致 谢 感谢审稿专家和编辑部的支持和鼓励.
参考文献
[1] Bartels J. 1957. Gezeitenkraefte[J]. Handb D Physik, 48:734-744.
[2] Capitaine N, Wallace P T, Chapront J. 2003. Expressions for IAU 2000 precession quantities[J]. Astronomy and Astrophysics, 412:567-586.
[3] Dahlen F A. 1993. Effect of the earth's ellipticity on the lunar potential[J]. Geophysical Journal International, 113:250-251.
[4] Fukushima T. 2003. New Determination of Precession Formulas[J]. Astronomical Journal, 126:494-534.
[5] Petit G, Luzum B. 2010. IERS conventions (2010), IERS Technical Note 36[R]. Frankfurt am Main:Verlag des Bundesamts für Kartographie und Geodäsie.
[6] Guo J Y. 2001. The fundamental of Geophysics (in Chinese)[M],BEIJING, Surveying and Mapping Press.
[7] Hartmann T, Wenzel H G. 1995a. Catalogue HW95 of the tide generating potential[J]. Bulletin D'informations Marées Terrestres, 123:9278-9301.
[8] Hartmann T, Wenzel H G. 1995b. The HW95 tidal potential catalogue[J]. Geophysics Research Letter, 22(24):3553-3556. dio:10.1029/95GL03324.
[9] Hao H T, Li H, Liu Z W, et al. 2010. Effect of earth flattening on precise calculation of tidal generation force[J]. Journal of Geodesy and Geodynamics (in Chinese), 30(17):6-9.
[10] Kudryavtsev S M. 2004. Improved harmonic development of the earth tide generating potential[J]. Journal of Geodesy, 77:829-838.
[11] Lei W W, Li K, Zhang H W. 2015. The Improvement and Comparison of the Empirical Formula for Transformation between Universal Time and Terrestrial Time[J]. Journal of Spacecraft TT&C Technology (in Chinese), 34(6):in Press.
[12] Li G Y. 2010. Celestial reference system transform and its applications (in Chinese)[M],BEIJING, Science Press.
[13] Li G Y. 2015. Astrometry and celestial mechanics foundation (in Chinese)[M],BEIJING, Science Press.
[14] Liu F G, Wang J. 2013. Relations of the planets revolution, sun tidal force and Gravitation deriving from the planets with the solar activity periodicity[J]. Progress in Geophysics (in Chinese), 28(5):2229-2240,doi:10.6038/pg20130504.
[15] Liu J C. 2012. The establishment, realization, and transformation of new astronomical reference systems (in Chinese)[Ph. D. thesis]. Nanjing:Nanjing University.
[16] Roosbeek, F. 1996. RATGP95:a harmonic development of the tide-generating potential using an analytical method[J]. Geophysical Journal International, 126(1):197-204.
[17] Soffel M, Langhans R. 2013. Space-Time Reference Systems[M]. Heidelberg New York Dordrecht London:Springer-Verlag.
[18] Wilhelm H. 1983. Earth's flattening effect on the tidal forcing field[J]. Journal of Geophysics, 52:131-135.
[19] Wenzel H G. 1974. The correction of tidal force development to ellipsoidal normal[J]. Bulletin D'informations Marées Terrestres, 68:3784-3790.
[20] Xi Q W. 1999. The influence of earth's flattening on tidal generating potential[J]. Progress in Natural Science (in Chinese), 9(10):925-929.
[21] Zhang H W, Xu H Z, Zhang C. 2005. Nutation sequence of the rigid earth determined by expansion of precise tidal generating potential[J]. Chinese Journal of Geophysic (in Chinese), 48(3):567-573.
[22] Zhang H W, Zheng Y, Ma G F. 2010. Re-derivation for influence of earth's flatting on TGP[J]. Journal of Geodesy and Geodynamics (in Chinese), 30(4):98-101.
[23] 郭俊义.2001.地球物理学基础[M].北京:测绘出版社
[24] 郝洪涛,李辉,刘子维,等.2010.高精度引潮力计算中地球扁率的影响[J].大地测量与地球动力学,30(17):6-9.
[25] 雷伟伟,李凯,张捍卫.2015.世界时与地球时转换经验公式的改进与比较[J].飞行器测控学报,34(6):(已接受,待发表).
[26] 李广宇. 2010.天球参考系变换及其应用[M].北京:科学出版社.
[27] 李广宇. 2015.天体测量和天体力学基础[M].北京:科学出版社.
[28] 刘复刚,王建.2013.行星系统运动、太阳引潮力和引力的变化与太阳运动周期律的关系[J].地球物理学进展,28(5):2229-2240,doi:10.6038/pg20130504.
[29] 刘佳成.2012.新天文参考系若干问题的研究[博士论文].南京:南京大学.
[30] 郗钦文.1999.地球扁率对引潮位的影响[J].自然科学进展,9(10):925-929.
[31] 张捍卫,许厚泽,张超.2005.应用精密引潮力位展开建立刚体地球章动序列[J].大地测量与地球动力学,48(3):567-573.
[32] 张捍卫,郑勇,马高峰.2010.地球扁率对引潮力位影响的重新推导[J].大地测量与地球动力学,30(4):98-101.