地球物理学进展  2015, Vol. 30 Issue (6): 2433-2439   PDF    
引用本文
蔡剑华, 肖晓. 2015. 基于小波自适应阈值去噪的MT信号处理方法[J]. 地球物理学进展, 30(6): 2433-2439, doi: 10.6038/pg20150601  
CAI Jian-hua, XIAO Xiao. 2015. Method of processing magnetotelluric signal based on the adaptive threshold wavelet. Progress in Geophysics, 30(6): 2433-2439, doi: 10.6038/pg20150601   
基于小波自适应阈值去噪的MT信号处理方法
蔡剑华1, 肖晓2    
1. 湖南文理学院信息研究所, 常德 415000;
2. 中南大学地球科学与信息物理学院, 长沙 41000
收稿日期: 2014-09-10 修回日期: 2015-10-02.
基金项目: 国家自然科学基金项目(41304098)、湖南省自然科学基金项目(12JJ4034)、湖南省教育厅青年项目(13B076)、湖南省重点建设学科-光学基金、湖南省重点实验室"光电信息集成与光学制造技术"和"湖南省光电信息技术校企联合人才培养基地"联合资助.
作者简介: 蔡剑华,男,1979年生,湖南郴州人,博士,副教授,从事大地电磁数据处理的研究.(E-mail:cjh1021cjh@163.com)
摘要: 针对常用大地电磁(magnetotelluric,MT)信号小波阈值去噪中阈值函数和阈值选取的不足,选取一种新的阈值函数,并提出了基于小波变换多分辨Stein无偏风险估计,自适应的获得最优阈值的方法;给出了新函数和自适应阈值的确定方法;在与小波硬、软阈值去噪、小波模极大值法去噪结果对比的基础上,用仿真实验验证了方法的可行性;最后用内蒙某地实测的大地电磁数据进行了去噪效果的对比研究.结果表明:本文选取的新函数和自适应阈值的确定方法是正确、有效的,克服了常用小波硬、软阈值去噪的缺点;去噪后大地电磁信号变得平稳,估算的响应参数方差减小,曲线更为圆滑、连续,为后续的地质解释和评价提供了更为准确的信息.
关键词: 大地电磁信号     阈值函数     自适应     小波阈值     去噪    
Method of processing magnetotelluric signal based on the adaptive threshold wavelet
CAI Jian-hua1, XIAO Xiao2    
1. Institute of Information, Hunan University of Arts and Science, Changde 415000, China;
2. School of geosciences and info-physics, Central south university, Changsha 41000, China
Abstract: In view of the deficiency from the wavelet threshold method commonly used in magnetotelluric signals procession, a new threshold function is given and the threshold is obtained adaptively based on Stein unbiased risk estimation in multi-resolution of wavelet transform. The determination method of new function and adaptive threshold is presented. Based on the comparison with wavelet hard threshold, soft threshold method and module maxima method, the proposed method is verified to be reliable from the simulation results. Finally some measured data from Inner Mongolia is processed similarly. The results show that the proposed method to determine the threshold function and the adaptive threshold is correct and effective. The new method overcomes the disadvantage from the traditional wavelet threshold method. After de-noising, magnetotelluric signals become stable, the variance estimation response parameters is reduced, and the parameter curve is more smooth and continuous. The better de-noised results provide more accurate information for subsequent geological interpretation and evaluation.
Key words: magnetotelluric signal     threshold function     adaptive     wavelet threshold     de-noising    
0 引 言大地电磁信号极其微弱，所以野外观测数据不可避免地会受到各种噪声的污染，同时又由于电磁噪声背景随着国家经济建设的发展而日益严重，导致大地电磁观测资料质量明显下降(王书明和王家映，2004；宁津生等，2004；汤井田等，2008；蔡剑华等，2010).近年来，小波阈值去噪，以及和经验模态分解相结合的小波阈值去噪方法，常用于大地电磁信号的处理(Trad and Travassos，2000；严家斌等，2008；武粤等，2012；蔡剑华等，2013).其中，最常用的阈值去噪方法主要有硬阈值法与软阈值法，方法本身有一些潜在的缺点，如硬阈值法的阈值函数具有不连续性，重构所得的信号会产生伪吉布斯效应(Mallat，1989；Trad and Travassos，2000；蔡剑华等，2013;汤井田等，2014)；而软阈值方法估计后的小波系数和分解得到的小波系数总存在恒定的偏差，直接影响着重构信号与真实信号的逼近程度，散失部分有用信号的信息(Mallat，1989；Trad and Travassos，2000，胡汉辉等2007).鉴于此，本文选取了一个新的阈值函数，且利用中点寻优算法获得函数参数，以克服硬软阈值法存在的不足，并提出了基于小波变换的Stein无偏风险估计算法自适应的确定各层阈值的方法，试图为大地电磁信号去噪处理提供新的技术手段. 1 阈值函数

本文选取了一个新的阈值函数，且利用寻优算法获得最优的函数参数，以克服阈值去噪方法中存在的不足.新阈值函数为

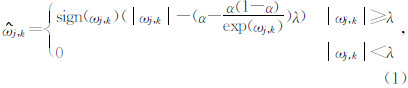
式中：α∈[0，1].当α分别取0和1值时，(1)式即成为硬阈值法和软阈值法；对于α∈(0，1)，该方法估计出来的系数介于软硬阈值法之间.由于采用单纯的软阈值法估计出来的j，k其绝对值总比ωj，k要小，因此要设法减小此偏差，但若把这种偏差减小为0就成了硬阈值情况(张旭东等，2007；林杰等，2011).因此，令 |ωj，k |的取值介于| ωj，k| －λ与 |ωj，k| 之间可能会使估计出来的小波系数j，k更加接近于理想值.基于此，把在公式(1)中的α因子可以看成一个自变量，而将去噪效果SNR看成α的函数，采用寻优算法寻优，以找到使SNR最大的α取值(Donoho，1995; 林杰等，2011).

本文采用的寻优算法为中点法，算法的详细内容请见文献(朱艳芹和杨先麟，2008；林杰等，2011).用中点法寻优求取α值的过程可描述为：

(1)对公式(1)中的参数α给出初始值 α1=0和α2=1，令i=1，N为算法需要迭代的次数.

(2)分别将参数α取值α1和α2，对信号进行去噪处理，计算去噪后信号的信噪比SNR1和SNR2.

(3)计算α1和α2的中点αmid=(α1+α2)/2，并代入阈值函数，对信号进行去噪处理，计算去噪后信号的信噪比SNRmid.

(4)计算SNR以α为变量的函数在α点处的微分值SNR′.如果SNR′≥0，则α1=αmid，SNR1=SNRmidd，否则α1=αmid，SNR2=SNRmid.

(5)判断i>N是否成立，否则令i < i+1，返回步骤(2)，成立则算法结束，此时α{mid则为最优的阈值参数，对应的SNRmid为最大的信噪比.

2 自适应阈值算法

假设信号为S(t)=f(t)+n(t)，f(t)为有用信号，n(t)为噪声，信号长度为N.带噪信号S(t)在规范正交基B下分解为高频小波系数HB[m]和低频小波系数LB[m]，其中B={gm}，0≤m < N，gm为滤波器系数，m为分解层次下的小波系数个数，且满足：

式中，SB(m)为S(t)的小波系数，有用信号f(t)可通过一个决策算子D由S(t)估计得到，决策算子D是正交基B下的投影，所得的估计函数为(Zheng and Zhang，2007；谢庆明等，2010)

其中，dm为阈值函数，此处采用本文选用的阈值函数如公式(1)所示.为了提高信号的信噪比，可以通过最小化风险估计，计算自适应于小波分解系数的阈值.设R=(f，λ)为阈值λ时的估计风险函数，λ可以通过求极小化的R=(f，λ)而被优化求解.Donoho认为可用 |SB(m)| 2－σ2来估计| HB |m 2，所得的估计函数为(谢庆明等，2010；邵忍平等，2012)

其中，σ为噪声的方差，Donoho已证明可由小波系数的中值来估计噪声的方差(Donoho，1995)

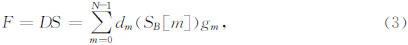
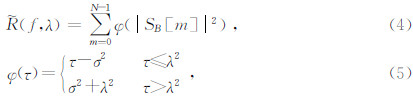
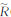此时，(f，λ)就是Stein的无偏风险估计函数.将N个小波系数SB(m)以降序排列，寻找第l个小波系数，满足SB[l]≤λ≤SB[l+1]，则式(4)可以改写为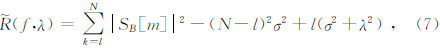

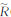多次迭代估计可求取最小化的(f，λ)，确定l，取得阈值λ=SB[l].将阈值选取自适应于尺度2j，可求得每个分解尺度上的阈值，则可形成多分辨率的自适应阈值算法.

3 仿真分析

按照上述确定阈值函数和自适应阈值的算法，将每一级尺度都看作是相互独立的，计算出一个与之最匹配的阈值进行降噪，最后再用各个尺度上软阈值降噪处理后的小波系数来重构信号，达到去噪的目的.首先，以常用的含噪声小波测试数据“Heavy sine”信号在不同噪声环境下所得的含噪信号作为实验对象，来验证本文方法的去噪效果.本文采用“Sym6”为小波基，小波分解层数定为7层.在Matlab7.0.1环境下，分别取传统的硬、软阈值去噪方法、模极大值去噪与本文算法的去噪效果加以比较.阈值采用Donoho等人的理论取λi=σi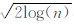，σi的取值如公式(6)所示，n为信号长度.为验证方法的可行性，处理了3种不同噪声强度下的“Heavy sine”信号.表 1列出了4种方法对3种加噪“Heavy sine”信号去噪后的信噪比SNR和均方根误差RMSE的参数对比：

表 1 4种方法去噪效果对比 Table 1 Comparison of de-noising effect for 4 methods

图 1所示为输入信号SNR=15.69时，4种方法对“Heavy sine”加噪信号的去噪结果.由表 1的评价参数和图 1的时域图对比可见，在不同强度的噪声背景下，所用4种方法均能够较好地完成对信号的去噪.其中：硬阈值的去噪曲线较为平滑，但丢失了该信号的局部特征；软阈值的去噪曲线存在一定的毛刺；模极大值法整体较好，但峰值不突出；而本文提出的算法能够较好地滤除噪声信号，并恢复信号的特征信息，去噪后信号折点和峰值信息更突出，本文去噪算法优于其他3种方法.计算的SNR也越大，RMSE也越小，相比硬阈值的去噪结果，本文去噪算法的处理结果SNR由22.78提高到24.58，RMSE则由0.227减小到了0.151.

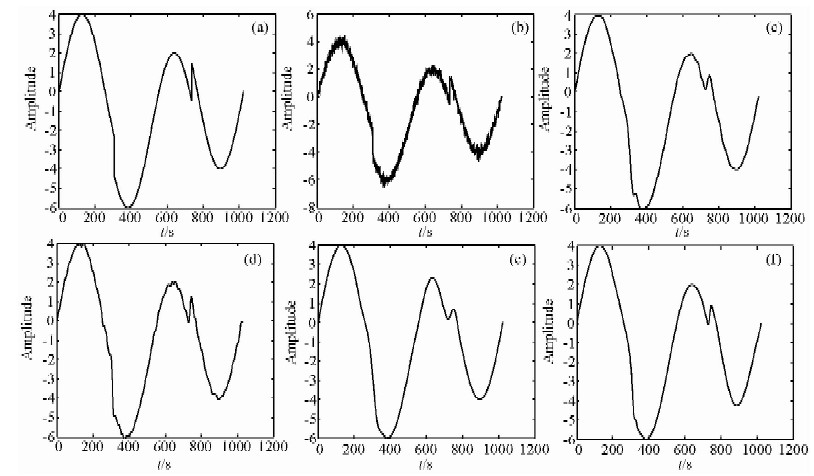图 1 仿真信号4种去噪方法处理结果对比
(a)原始信号; (b) 加噪信号(SNR=15.69); (c) 硬阈值方法处理结果; (d) 软阈值方法处理结果; (e) 模极大值方法处理结果; (f)本文方法处理结果. Fig. 1 Comparison of de-noised results from 4 kinds of de-noising method
(a)Original signal; (b) Noised signal(SNR=15.69); (c)Results processed by hard-threshold method; (d)Results processed by soft-threshold method;(e)Results processed by modulus maximum method;(f)Results processed by proposed method.
4 实测数据处理

实测数据是来自内蒙毛登某矿区某测点的EH-4数据，数据受到各种噪声的干扰很大，甚至掩盖了有用信号的峰值，时间序列如图 2所示.可见，噪声主要影响了电道的信号，对磁场的信号也有一定的干扰.为量化比较去噪效果，先给出去噪前两个电道信号的统计参数:

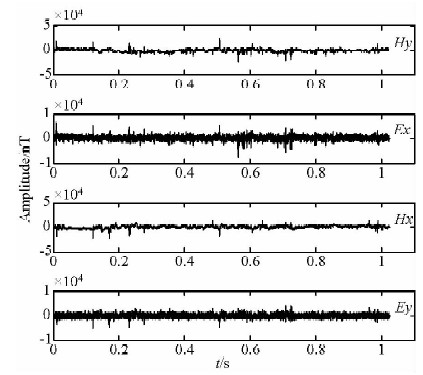图 2 实测大地电磁信号的时间序列 Fig. 2 Time series of measured MT signal

Ex数据的统计参数为：最大值6.0494×103 mV，最小值-7.2355×103 mV，均值282.9287 mV，方差6.1235×105，能量为8.5076×109 mV2；

Ey数据的统计参数为：最大值3.9017×103 mV，最小值-5.1824×103 mV，均值13.7152 mV，方差5.3341×105，能量为6.5564×109 mV2.

采用本文提出的阈值函数和自适应阈值去噪方法对上面给出的原始数据做去噪处理，并与硬、软阈值去噪，模极大值去噪的结果进行对比，去噪后的数据如图 3所示.从图 3可见，4种方法都对噪声有了很大程度的抑制，去噪后信号的细节得到了凸显.为节约篇幅，仅列出Ex数据的统计参数，Ey数据的统计规律同Ex数据.去噪后的Ex数据量化统计参数为分别为：

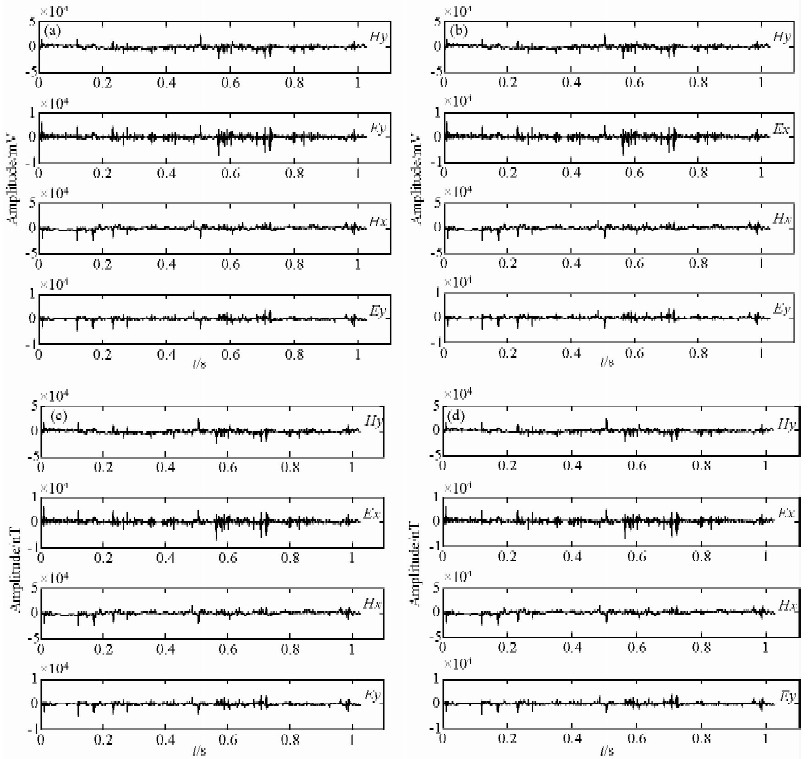图 3 实测数据4种去噪方法处理结果对比
(a) 硬阈值方法处理结果； (b) 软阈值方法处理结果；(c) 模极大值方法处理结果； (d)本文方法处理结果. Fig. 3 Comparison of processed results of MT data for 4 kinds of de-noising methods
(a)Results processed by hard-threshold method；(b)Results processed by soft-threshold method； (c)Results processed by modulus maximum method；(d)Results processed by proposed method.

硬阈值去噪后：最大值5.8997×103 mV，最小值-7.0283×103 mV，均值286.7846 mV，方差3.1061×105，能量为4.8271×109 mV2；

软阈值去噪后：最大值5.8981×103 mV，最小值-6.9911×103 mV，均值287.0067 mV，方差3.1046×105，能量为4.8269×109 mV2；

模极大值法去噪后：最大值5.8910×103 mV，最小值-7.0045×103 mV，均值286.7536 mV，方差3.1033×105，能量为4.8234×109 mV2；

本文方法去噪后：最大值5.8931×103 mV，最小值-7.0039×103 mV，均值286.7881 mV，方差3.1031×105，能量为4.8234×109 mV2.

从统计的数据可以看到，噪声的能量很大，它的存在将使得阻抗的估算很不稳定；去噪后信号的方差都减小了，能量也减小到了原来的近一半，改正后信号变得平稳，峰值等细节得到了凸显；再者，从时域图和统计参数来看本文算法取得的去噪效果也优于其他3种方法.

用去噪前后的数据分别计算电阻率曲线ρxy和ρxy，图 4 对比了4种方法去噪前后估算的阻抗参数曲线ρxy，图 5对比了相应的电阻率曲线ρxy.此处，用方差(VAR)，曲线平滑系数(SNS)来评估去噪前后两参数曲线的平稳性，用曲线相似性参数(NCC)从整体上评价去噪前后两参数曲线的相似程度即整体趋势.曲线平滑系数和曲线相似性参数定义如下(彭建亮等，2012)：

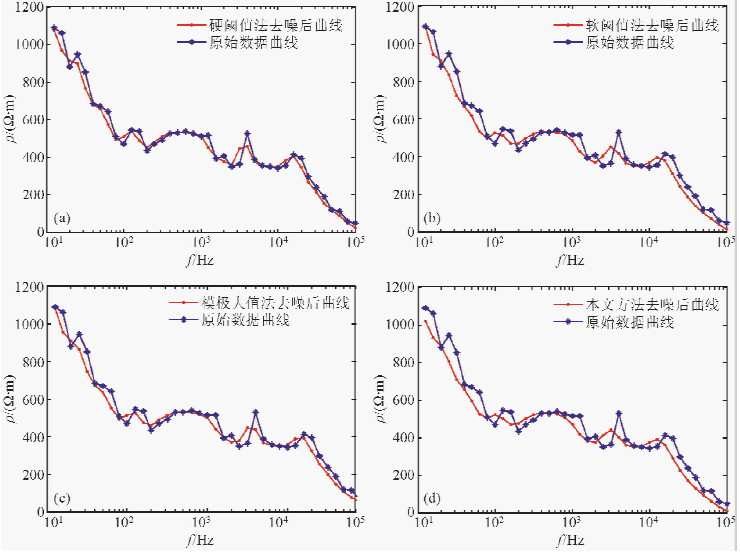图 4 4种方法去噪前后的ρxy曲线对比
(a) 硬阈值方法处理结果； (b) 软阈值方法处理结果；(c) 模极大值方法处理结果； (d)本文方法处理结果. Fig. 4 Comparison of ρxy curve before and after de-noising for 4 kinds of methods
(a)Results processed by hard-threshold method；(b)Results processed by soft-threshold method； (c)Results processed by modulus maximum method；(d)Results processed by proposed method.

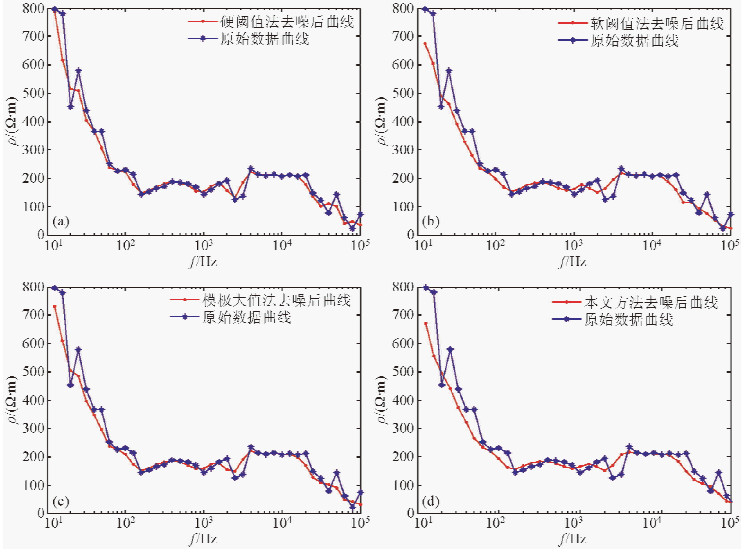图 5 4种方法去噪前后的ρyx曲线对比
(a)硬阈值方法处理结果； (b) 软阈值方法处理结果；(c) 模极大值方法处理结果； (d)本文方法处理结果. Fig. 5 Comparison of ρyx curve before and after de-noising for 4 kinds of methods
(a)Results processed by hard-threshold method；(b)Results processed by soft-threshold method； (c)Results processed by modulus maximum method；(d)Results processed by proposed method.

(1)曲线平滑系数

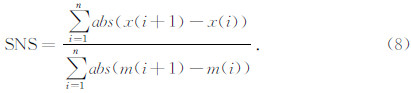
(2)曲线相似性参数

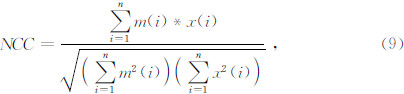
式(8)中m(i)为4种去噪方法消噪后计算所得视电阻率所求的均值，x(i)为各种方法消噪后的视电阻率，系数越小说明曲线越平滑；式(9)中，m(i)和x(i)的取值与式(8)同，NCC的值在-1~1之间，-1代表变换前后两数据波形反向，0代表两波形正交；1代表完全相同.

表 2给出了4种方法计算的电阻率曲线ρxy和ρxy的方差、曲线平滑系数和曲线相似性参数.其中去噪前计算的ρxy曲线的方差是8.9939×104，ρxy曲线的方差是3.1012×104.由图 4、图 5和表 2数据的对比可知，消噪前后计算电阻率曲线ρxy和ρxy整体趋势是一致的，计算的曲线相似性参数都在0.9以上.但去噪前后曲线细节得到了明显的改善，去噪前存在少数不平滑和飞点的情况，去噪后某些飞点得到了有效的抑制，所有响应曲线的误差棒平均值都减小了，曲线也更加圆滑、连续，参数的估算变得稳定；相比传统硬阈值方法，本文提出的方法去噪结果更好，ρxy电阻率曲线方差由8.4805×104减小到7.8493×104，曲线平滑系数由37.89减小到33.75，线相似性参数则由0.9162提高到0.9647，ρxy电阻率曲线也表现出相同的规律.说明在相同信噪比的情况下，用本文方法处理后的曲线更为平稳，资料质量有更明显的改善，为大地电磁信号的去噪提供了一种更好的途径.

表 2 4种方法去噪后曲线参数对比 Table 2 Comparison of curve parameters after de-noising for 4 methods
5 结论

5.1      为适应大地电磁信号去噪的要求，针对目前小波硬、软阈值去噪方法存在的不足，本文提出了一种小波自适应阈值去噪方法.该方法采用一个新的阈值函数，克服了传统软、硬阈值函数的缺陷，并基于小波变换的多分辨率Stein无偏风险估计自适应的确定阈值，在不同分解尺度下采用自适应阈值去.

5.2       噪的方法能有效的消除大地电磁信号中的噪声.仿真和实测数据处理结果表明，在相同信噪比的情况下，本文提出的小波自适应阈值去噪方法，比传统的小波硬、软阈值和模极大值法效果更好，能获得更好的去噪效果，为进一步的反演和地质解释工作提供更为准确的资料.

致谢 感谢审稿专家和编辑部的帮助和支持.
参考文献
[1] Cai J H, Hu W W, Ren Z Y, et al. 2010. Magnetotelluric data processing and simulation based on higher-order statistics[J]. Journal of Central South University (Science and Technology) (in Chinese), 41(8):1556-1560.
[2] Cai J H, Wang X C, Hu W W. 2013. A method for MT data denoising based on empirical mode decomposition and wavelet threshold[J]. Oil Geophysical Prospecting (in Chinese), 48(2):303-307.
[3] Chipman H A, Kolaczyk E D, MeCulloch R E. 1997. Adaptive Bayesian wavelet shrinkage[J]. Journal of the American Statistical Association, 92(440):1413-1421.
[4] Donoho D L. 1995. De-noising by soft-thresholding[J]. IEEE Transaction on Information Theory, 41(3):613-627.
[5] Donoho D L, Johnstone I M. 1995. Adapting to unknown smoothness via wavelet shrinkage[J]. Journal of the American Statistical Association, 90(432):1200-1224.
[6] Hu H H, Yang H, Tan Q, et al. 2007. Sintering fan faults diagnosis based on wavelet analysis[J]. J. Cent. South Univ. (Science and Technology) (in Chinese), 38(6):1169-1173.
[7] Lin J, Fu M Y, Li D P. 2011. Self-adaptive wavelet threshold de-noising method and its application in image processing[J]. Acta Armamentarii (in Chinese), 32(7):896-900.
[8] Mallat S G. 1989. A theory for multiresolution signal decomposition:the wavelet representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11(7):674-693.
[9] Ning J S, Wang H H, Luo Z C. 2004. Applications of wavelet analysis in geodesy and its progress[J]. Geomatics and Information Science of Wuhan University (in Chinese), 29(8):659-663.
[10] Peng J L, Peng Z M, Zhang J, et al. 2012. De-noising method of seismic signal based on adaptive filtering in fractional domain[J]. Progress in Geophysics (in Chinese), 27(4):1730-1737, doi:10.6038/j.issn.1004-2903.2012.04.054.
[11] Shao R P, Cao J M, Li Y L. 2012. Gear fault pattern identification and diagnosis using time-frequency analysis and wavelet threshold de-noising based on EMD[J]. Journal of Vibration and Shock (in Chinese), 31(8):96-101, 106.
[12] Tang J T, Hua X R, Cao Z M, et al. 2008. Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data[J]. Chinese J. Geophys. (in Chinese), 51(2):603-610, doi:10.3321/j.issn:0001-5733.2008.02.034.
[13] Tang J T, Li J, Xiao X, et al. 2014. Mathematical morphology filtering and noise suppression of magnetotelluric sounding data[J]. Chinese Journal of Geophysics (in Chinese), 55(5):1784-1793, doi:10.6038/j.issn.0001-5733.2012.05.036.
[14] Trad D O, Travassos J M. 2000. Wavelet filtering of magnetotelluric data[J]. Geophysics, 65(2):482-491.
[15] Wang S M, Wang J Y. 2004. Analysis on statistic characteristics of magnetotelluric signal[J]. Acta Seismologica Sinica (in Chinese), 26(6):669-674.
[16] Wu Y, Meng X H, Li S L. 2012. Wavelet analysis and its application in geophysics of China[J]. Progress in Geophysics (in Chinese), 27(2):750-760, doi:10.6038/j.issn.1004-2903.2012.02.043.
[17] Xie Q M, Xiao L Z, Liao G Z. 2010. Application of SURE algorithm to echo train de-noising in low field NMR logging[J]. Chinese J. Geophys. (in Chinese), 53(11):2776-2783, doi:10.3969/j.issn.0001-5733.2010.11.027.
[18] Yan J B, Liu G Z, Liu J X. 2008. Application of wavelet transform in processing nature electromagnetic field time series[J]. Geology and Prospecting (in Chinese), 44(3):75-78.
[19] Zhang X D, Zhang Y, Ma Y Q. 2007. Approaches of denoise by wavelet ferent signals[J]. Oil Geophysical Prospecting (in Chinese), 42(Supplement):119-123.
[20] Zheng C X, Zhang Y M. 2007. Low-field pulsed NMR signal denoising based on wavelet transform[C]. //IEEE 15th Signal Processing and Communications Applications.Eskisehir:IEEE, 1-4.
[21] Zhu Y Q, Yang X L. 2008. Several new methods based on wavelet thresholding denoising[J]. Electronic Test (in Chinese), (2):18-22.
[22] 蔡剑华,胡惟文,任政勇,等. 2010.基于高阶统计量的大地电磁数据处理与仿真[J].中南大学学报(自然科学版), 41(8):1556-1560.
[23] 蔡剑华,王先春,胡惟文. 2013.基于经验模态分解与小波阈值的MT信号去噪方法[J].石油地球物理勘探, 48(2):303-307.
[24] 胡汉辉,杨洪,谭青,等. 2007.基于小波分析的风机故障诊断[J].中南大学学报(自然科学版), 38(6):1169-1173.
[25] 林杰,付梦印,李道平. 2011.自适应小波阈值去噪算法及在图像处理中的应用[J].兵工学报, 32(7):896-900.
[26] 宁津生,汪海洪,罗志才. 2004.小波分析在大地测量中的应用及其进展[J].武汉大学学报·信息科学版, 29(8):659-663.
[27] 彭建亮,彭真明,张杰,等. 2012.基于分数域自适应滤波的地震信号去噪方法[J].地球物理学进展, 27(4):1730-1737, doi:10.6038/j.issn.1004-2903.2012.04.054.
[28] 邵忍平,曹精明,李永龙. 2012.基于EMD小波阈值去噪和时频分析的齿轮故障模式识别与诊断[J].振动与冲击, 31(8):96-101, 106.
[29] 汤井田,化希瑞,曹哲民,等. 2008. Hilbert-Huang变换与大地电磁噪声压制[J].地球物理学报, 51(2):603-610, doi:.10.3321/j.issn:0001-5733.2008.02034.
[30] 汤井田,李晋,肖晓,等. 2014.数学形态滤波与大地电磁噪声压制[J].地球物理学报, 55(5):1784-1793, doi:10.6038/j.issn.0001-5733.2012.05.036.
[31] 王书明,王家映. 2004.大地电磁信号统计特征分析[J].地震学报, 26(6):669-674.
[32] 武粤,孟小红,李淑玲. 2012.小波分析及其在我国地球物理学研究中的应用进展[J].地球物理学进展, 27(2):750-760, doi:10.6038/j.issn.1004-2903.2012.02.043.
[33] 谢庆明,肖立志,廖广志. 2010. SURE算法在核磁共振信号去噪中的实现[J].地球物理学报, 53(11):2776-2783, doi:10.3969/j.issn.0001-5733.2010.11.027.
[34] 严家斌,刘贵忠,柳建新. 2008.小波变换在天然电磁场信号时间序列处理中的应用[J].地质与勘探, 44(3):75-78.
[35] 张旭东,詹毅,马永琴. 2007.不同信号的小波变换去噪方法[J].石油地球物理勘探, 42(增刊):118-123.
[36] 朱艳芹,杨先麟. 2008.几种基于小波阈值去噪的改进方法[J].电子测试, (2):18-22.