2. 中国地质科学院地球物理地球化学勘查研究所, 廊坊 065000
2. Institute of Geophysical and Geochemical Exploration CAGS, Lang fang 065000, China
瞬变电磁正演是研究瞬变电磁响应规律的有效途径,随着计算机技术的应用,瞬变电磁正演方面有了很快的发展(殷长春等,1994;李貅,2002;王华军,2003;熊彬等,2006).而时域有限差分法(Finite-Difference Time-Domain,简称FDTD)是电磁场计算领域的一种常用方法.自1993年Wang和Hohmann实现了瞬变电磁法的FDTD算法以来(Oristaglio,1984;Adhidjaja,1989;Commer,2004;Commer,2006),目前该算法已经获得了较大的进展(许洋铖,林君等,2012;孙怀凤,李貅等,2013;李建慧等,2013;李展辉等,2014).目前的FDTD算法可以实现地面、隧道、地-空、地-井等装置的三维模拟(王建,1996年;李貅,武军杰等,2006;岳建华,2007;宋汐瑾等,2011;孟庆鑫,2012;殷长春,2013;卢绪山,2014).FDTD三维正演中几何建模和网格剖分是瞬变电磁三维正演模拟的重要组成部分.目前瞬变电磁三维正演模拟中以简单几何体(如板状体、球体、圆柱体等)的正演模拟为主(殷长春,刘斌等,1994;汤井田等,2010;蒋大青,2012),而对于复杂模型尚缺乏有效的建模工具.所以,针对复杂模型的FDTD数值模拟,选择一种高效、高精度的建模方法,对于提高瞬变电磁FDTD正演效率极为重要.
由于复杂目标三维几何建模及Yee元胞格式的网格剖分的困难性,国内学者对于FDTD的Yee元胞格式网格剖分已有一些研究,大致分为三种:第一种根据目标特点进行拆分,对各部件单独处理并拼接在一起(阎玉波,1998);第二种采用CAD技术通过VBA或Auto-LISP语言二次开发,从而实现模型的Yee元胞的网格剖分(李明之等,1999;莫锦军,2004;张秋菊,2005);第三种是基于目标的三角面元模型,采集模型的网格信息(普鑫,2006;杨利霞,2006;梁慧,2009).但这些方法,并没有形成一套完整的分析软件包.而且开发难度大,不具备通用性,针对复杂模型,这些方法还不太完善.国外针对FDTD三维建模及网格剖分,已有一些功能强大的商业软件,应用较为广泛的通用软件有:XFDTD、QFDTD90、EMU/FDTD和FDTD-Solver等(Srisukh,2003;RaiMittra,2008;MacGillivray,2008),但这些软件只适合于微波、雷达、天线等高频数值模拟,针对地球物理电磁法勘探领域数值模拟,目前还未见成熟的商业软件.
经过调研,西班牙巴塞罗那国际工程计算方法研究中心开发的GID软件能够快速建立几何模型,并能实现结构化和非结构化的网格剖分.该软件功能强大,图形用户界面友好,适应性强,最重要的是可以为FDTD数值模拟提供是三维可视化的几何建模及Yee元胞格式的网格剖分.不过GID软件虽然具备Yee元胞形式的网格剖分,但功能还不完善,缺乏必要的输出,从而不能直接应于瞬变电磁FDTD计算.为了能够满足FDTD计算需求,作者对GID软件进行二次开发,通过编写代码,得到FDTD计算所需的节点的数据,从而用于瞬变电磁三维FDTD正演计算.最后作者结合课题组在研项目,针对不同类型的目标体进行了建模及数值模拟.结果表明,应用GID软件建模,使得复杂模型的瞬变电磁三维正演模拟成为可能,使得FDTD算法精细模拟的特点更加突出.
1 GID软件二次开发GID具有类似CAD的系统,可以方便快捷地建立几何模型,同时提供用于有限差分的笛卡尔网格剖分器,这为FDTD数值模拟提供了条件.但是GID软件缺乏现成的边界条件、材料库、单位以及用户所需的文本文件格式及内容,已开发的一些接口不适用等.建立几何模型和网格剖分之后,只能输出.msh后缀文件,这文件还只包含了节点和节点坐标.由于没有建立好的材料库,不能对模型添加材料及其属性.因此,在进行有限差分数值模拟前,需要对它进行二次开发,编写材料库,及自定义输出文本格式等.
1.1 编写材料库当在GID软件里面建立三维模型后,需要为模型添加属性信息.用户通过利用内置的.BAS后缀文件控制模型材料属性.FDTD所需材料及属性内定的格式如下:
MATERIAL: material_name
QUESTION: field_name[‘#CB#’(...,optional_value_i,...)]
VALUE: default_field_value
END MATERIAL
其中MATERIAL为材料名称,QUESTION为材料多种属性,VALUE为材料默认值大小.当对线、面、体添加材料,对模型网格剖分,材料属性自动转到单元上.
1.2 定义输出文件根据FDTD数值模拟所需模型文本文件要求,需要对GID的输出文本文件重新定义,给出满足FDTD计算需要的文本文件,主要是编写后缀为(.BAS)的文件.该文件经GID处理后产生存储几何、物理信息的数据文件文本,文件代码采用类似于脚本语言的写法,其主要语句如下:
GEOMETRY
& ELEMENT CONNECTIVITIES
& ELEM. MATER. CONNECTIVITIES
*loop elems
*elemsnum *elemsmat *elemsConec
*end elems
& NODAL COORDINATES
&NODE COORD.X COORD.Y COORD.-Z
*loop nodes
*format "%6i%15.5f%15.5f%15.5f"
*NodesNum *NodesCoord
*end
END_GEOMETRY
其中前面带有“*”的为程序内定的变量或命令,例如上面语句*loop elems表示单元循环,*elemsum表示输出单元个数,*elemsmat表示输出单元材料,*elemsConec表示输出单元上节点,*loop nodes*表示节点循环,*NodesNum表示输出节点编号和节点坐标,*format表示输出结果字节长度.而未带*号代表注释行,经GID原样输出到.DAT文件.
1.3 调用脚本语言GID提供的.BAS文件控制的输出主要用于有限元,其GID提供的笛卡尔网格剖分器,则专门用于有限差分信息输出,所以单纯依靠.BAS文件不能完全输出有限差分所需信息,需要在.BAS文件中调用脚本语言.编写*TCL命令,然后用脚本语言(TCL)编写输出内容,其语言结构如下:
procInitGIDProject { dir } {
}
procBeforeInitGIDPostProcess {} {
}
procInitGIDPostProcess {} {
...body...
set value ...
return &value
}
上述代码采用TCL形式结构,通过调用GID内部函数,返回值.
procGetIjkFromNum { numgrid_nigrid_nij } {
incrnum -1
set k [expr &num/&grid_nij]
set rest [expr &num%&grid_nij]
set j [expr &rest/&grid_ni]
set i [expr &rest%&grid_ni]
return "&i &j &k"
}
上述代码主要是为了把有限元的节点编号做一个转换,变成有限差分形式的节点排列方式,转换成X,Y,Z三个方向的索引号,同时调用如下函数语句:
setpmin [GiD_Cartesian get corner]
setboxsize [GiD_Cartesian get boxsize]
setngridpoints [GiD_Cartesian get ngridpoints]
set dimension [GiD_Cartesian get dimension]
set coordinates [GiD_Cartesian get coordinates]
上述代码通过调用GID内部函数,得到有限差分所需的笛卡尔网格信息,依次输出网格剖分最小点位置,剖分网格范围,相邻网格尺寸,X、Y、Z方向的网格数目及三个方向的坐标,这都是有限差分所需的信息.
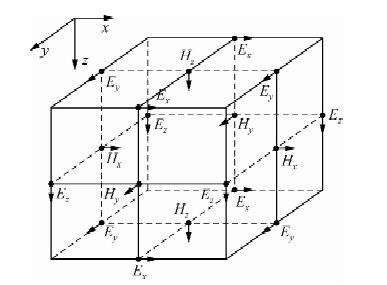
2 三维建模与数值模拟瞬变电磁三维数值模拟方法选择FDTD(孙怀凤,2013;卢绪山,2014),FDTD计算中要求的网格剖分为六面体Yee元胞交错网格格式,如图 1所示.本文数值模拟首先利用二次开发的GID软件进行可视化建模并进行六面体剖分,输出相应的网格节点及属性数据,然后利用FDTD软件进行三维正演计算.
|
图 1 FDTD计算采用的Yee元胞格式 Fig. 1 The Yee cell format of FDTD |
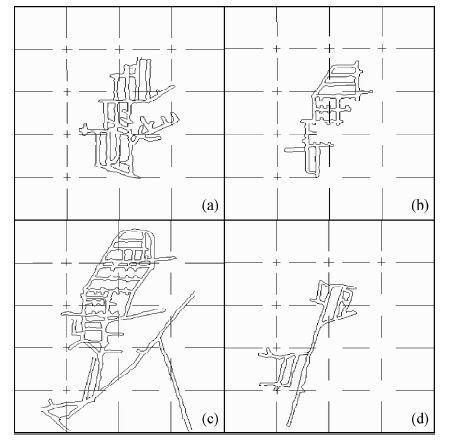
课题组在某地开展了地-空装置TEM勘查试验,探测目标为地下巷道.为对实际探测提供参考,课题组对地下巷道探测目标进行了三维数值模拟.工作区采掘巷道共有四层,如图 2所示.地表海拔约为90~100 m.激发方式选择电性源,AB=230 m,平行x轴,源中心点偏移矿体中心1000 m,接收海拔为120 m.
|
图 2 开采巷道平面分布 (a)海拔高度7 m;(b)海拔高度0 m; (c)海拔高度-10 m;(d)海拔高度-24 m. Fig. 2 Plane distribution of mining tunnel (a)Altitude 7 m;(b)Altitude 0 m; (c)Altitude -10 m;(d)Altitude -24 m. |
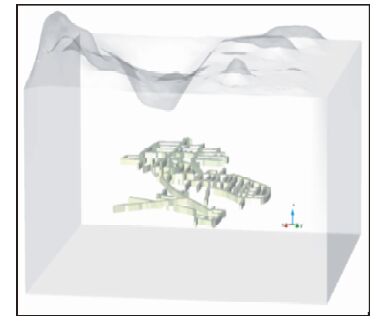
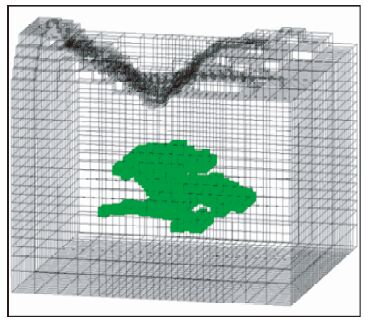
课题组采用GID软件根据原始平面巷道分布图,进行了三维建模.图 3为三维巷道模型,图中展示了地形的起伏以及探测目标的三维分布.同时由于实验目的是在低阻区域寻找高阻,为了减小边界误差,增加计算区域范围,在巷道外采用1.1的比率增加网格尺寸.最后利用GID软件的笛卡尔网格剖分器,对模型进行Yee元胞形式网格剖分.图 4为巷道体Yee元胞网格剖分后结果图,图中所有单元为正交直立六面体,巷道单元材料添加电阻率400 Ω·m.通过GID材料属性显示功能,区别背景材料值,显示巷道所属单元为绿色.
|
图 3 三维巷道模型图 Fig. 3 3D model diagram of tunnel |
|
图 4 三维网格剖分结果 Fig. 4 3D mesh division |
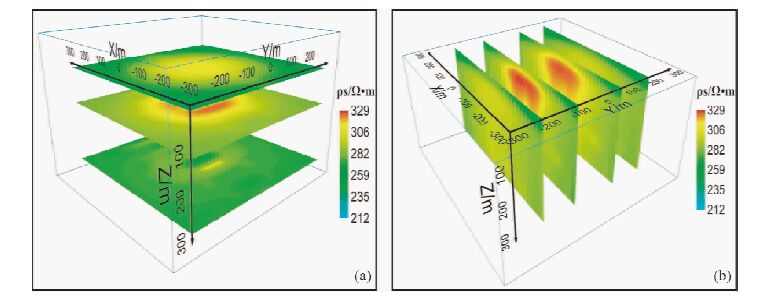
正演程序使用课题组编制的瞬变电磁法三维FDTD软件.图 5为不同方向全域视电阻率切片图(李貅,2015),图中可以看出,对于呈三维分布的地下巷道,通过GID软件三维建模、FDTD数值计算、全域视电阻率处理,能够可靠地反应其巷道中心位置,高阻异常体分布范围和模型吻合.
|
图 5 视电阻率切面图 (a)XY方向切片图;(b)YZ方向切片图. Fig. 5 Section map of apparent resistivity (a)Slice map in XY direction;(b)Slice map in YZ direction. |
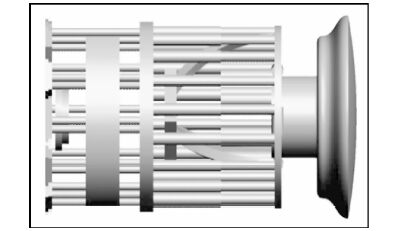
利用瞬变电磁进行隧道超前探测工作时,在TBM机施工的隧道中会受到TBM机严重干扰,使得瞬变电磁超前探测的效果大打折扣.为了研究消除TBM机干扰响应的方法,需要通过数值模拟来获取TBM机的瞬变电磁响应规律.由于双护盾TBM机(图 6)在生产中应用比较广泛,本文采用双护盾TBM机进行几何建模(图 8),计算其响应规律.

|
图 6 双护盾型TBM机结构图 Fig. 6 Structure diagram of double shield TBM |
|
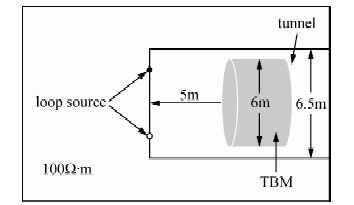
图 7 TBM机开挖隧道模型示意图 Fig. 7 The ketch diagram tunnel with TBM |
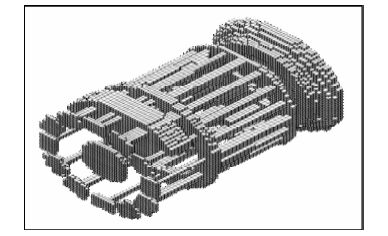
如图 7所示模型中(卢绪山,2014),在一个均匀全空间中存在一个已经开挖了的隧道空腔,在掌子面后方5 m处存在双护盾TBM机,TBM模型直径为6 m.由于模型尺寸相对较小,采用0.2 m的网格对其精细网格剖分(图 9),设定围岩电阻率为100 Ω·m.采用回线源激发,回线源长边长为3.2 m,激发电流为100A.首先对具有不同电阻率的TBM机模型进行正演计算,TBM机电导率取值分别为102 S/m、103 S/m、104 S/m、105 S/m、106 S/m和107 S/m.
|
图 8 双护盾TBM机模型 Fig. 8 TBM model with double shield |
|
图 9 TBM机网格剖分图 Fig. 9 Grid subdivision of TBM machine |
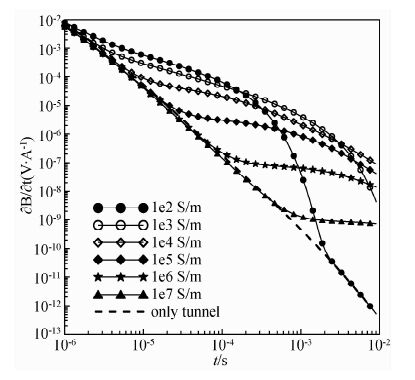
图 10为具有不同电阻率的TBM机开挖隧道模型在掌子面处回线源中心点处的垂直衰减曲线,其中虚线表示不存在TBM机时的隧道模型的响应.从图中可以看出,具有不同电导率的TBM机相对于隧道空腔来说所产生的瞬变电磁响应表现为典型的低阻异常特征,并且随着TBM机电导率的增加,低阻异常在衰减曲线中表现出规律性的变化.电导率越大,低阻异常出现的时间越靠后,并且衰减也越慢.由于正演模拟的时间长度有限,图中具有较大电导率的TBM机开挖隧道模型的衰减曲线并没有衰减到与隧道空腔曲线重合.
|
图 10 不同电导率的TBM机TEM响应曲线图 Fig. 10 TEM curves of TBM with different conductivity |
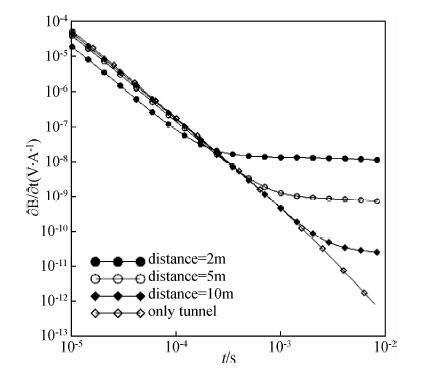
由于铁的电导率为107 S/m,因此将TBM机的电导率近似为107 S/m,模拟位于掌子面前面不同距离的TBM响应.将TBM机与掌子面的距离分别设置为2 m、5 m和10 m并计算其在掌子面出产生的瞬变电磁响应.图 11给出了四条衰减曲线,分别对应着TBM机与掌子面距离为2 m、5 m、10 m以及隧道空腔的响应.从图中可以看出,随着距离的增加,TBM机造成的异常在衰减曲线上出现的越晚,并且异常的幅值也越小.因此在施工中应该尽可能地让TBM机远离掌子面,使其产生的干扰影响变小.
|
图 11 TBM机与掌子面不同距离TEM响应曲线图 Fig. 11 TEM curves of TBM with different distance from tunnel face |
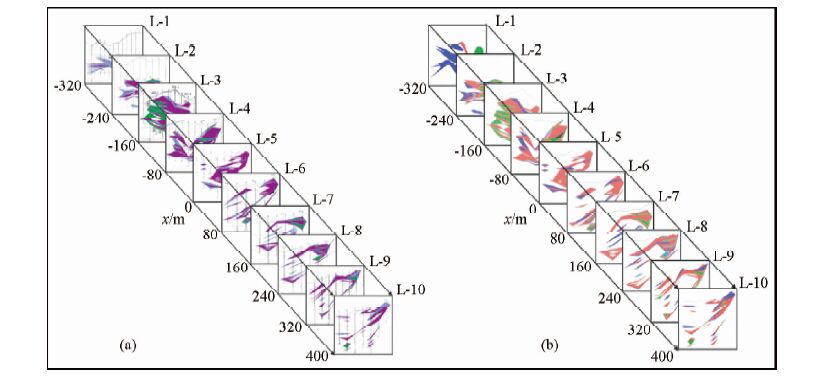
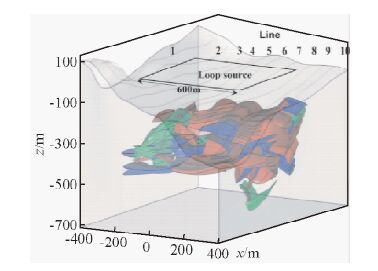
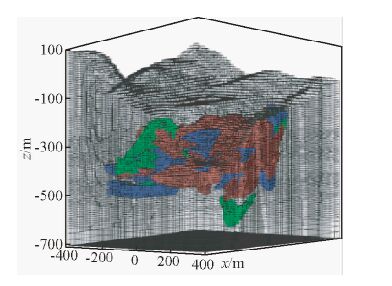
图 12为某铜镍矿体地质剖面图,图中展示1~10线的矿体分布情况,其中矿体分为铜镍矿、镍钴矿以及低含量镍矿.图 13为根据地质断面建立的地球物理模型,模型中对不同种类的矿体添加对应的电阻率值,其中红色为镍钴矿(电阻率设为10 Ω·m)、绿色为铜镍矿(电阻率设为20 Ω·m)、蓝色为低镍矿(电阻率设为50 Ω·m),围岩电阻率为500 Ω·m.图中还给出了测线以及发射框的位置.图 14为Yee元胞形式的网格剖分图.
|
图 12 铜镍矿体地质剖面图
(a)地质剖面图;(b)GID建模剖面图. Fig. 12 Geology profile map with copper and nickel (a)Geological profiles;(b)GID model profiles. |
|
图 13 三维矿体模型 Fig. 13 3D model of ore body |
|
图 14 Yee元胞形式的网格剖分 Fig. 14 Grid subdivision of Yee cell |
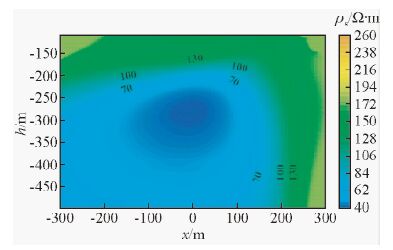
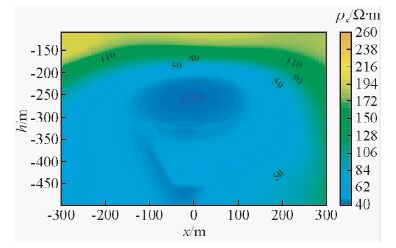
数据处理采用全域视电阻率方法,这里选L2线和L9线处理结果(李貅,2015).图 15中可以看出L2线在-200~100点号范围内存在低阻异常,为矿体的反应,异常中心在0号点附近,异常整体平缓,这与实际地质断面上的矿体分布基本是一致的.由于L2线下方矿体分布较为集中使得矿体在视电阻率断面图中显示为团块.图 16中L9线视电阻率断面等值线图,该图中细节相对更加丰富,除在-250 m深度显示的主体异常外,还在约330 m深度处出现微弱低阻异常,该异常对应地质断面上的矿体薄层.此外在-150~0点号范围内-400~-500 m深度处出现的陡倾异常,应为多个小薄层矿体的叠加反应.
|
图 15 L2线视电阻率断面图 Fig. 15 Apparent resistivity profile of line 2 |
|
图 16 L9线视电阻率断面图 Fig. 16 Apparent resistivity profile of line 9 |
三维可视化建模及复杂模型的瞬变电磁三维正演是目前的研究热点.本文基于GID商业软件,实现了复杂模型的三维可视化建模;通过对GID软件进行二次开发,获得了适合FDTD算法的网格剖分数据;从而实现复杂模型的几何建模及瞬变电磁三维FDTD正演计算.文中通过三种不同类型复杂模型的三维可视化建模及瞬变电磁三维正演计算,得到以下结论:
(1)利用GID软件强大的几何建模功能,实现了复杂模型的三维可视化建模.为瞬变电磁数值计算领域,提供简便易行的可视化建模方法,从而有助于瞬变电磁三维正演响应规律的探索,为瞬变电磁三维反演奠定基础.
(2)以GID的Cartesian网格剖分器为基础,对模型进行Yee元胞格式的网格剖分.该网格剖分方法,能很好的对模型进行网格剖分,相比基于传统三角面元的FDTD网格剖分方法,提高了效率和精度.
(3)文中通过实际生产中三种不同类型的复杂模型三维正演计算,采用全域视电阻率对计算结果进行了处理解释.通过分析电阻率断面图,能准确反映地下介质的电性分布,从而促进三维正演解释技术在生产实际的应用.
致 谢 感谢两位匿名评审专家和编辑部老师对本文内容和格式上的帮助,感谢中国地质科学院地球物理地球化学勘查研究所武军杰和智庆全对本文提出的宝贵意见,使本文质量大大提高,在此表示致谢!
| [1] | Adhidjaja J I, Hohmann G W. 1989. A finite-difference algorithm for the transient electromagnetic response of a three-dimensional body[J]. Geophysical Journal International., 98(2): 233-242. |
| [2] | Alimoradi A, Moradzadeh A, Naderi R, et al. 2008. Prediction of geological hazardous zones in front of a tunnel face using TSP-203 and artificial neural networks[J]. Tunnelling and Underground Space Technology, 23(6): 711-717. |
| [3] | Commer M, Newman G. 2004 .A parallel finite-difference approach for 3D transient electromagnetic modeling with galvanic sources[J]. Geophysics, 69(5): 1192-1202. |
| [4] | Commer M, Newman G A. 2006.An accelerated time domain finite difference simulation scheme for three-dimensional transient electromagnetic modeling using geometric multigridconcepts[J]. Radio Science, 41(3): n/a-n/a. |
| [5] | Chen L L, Liao C, Xia X Y. 2010. Auto dissection of entity with three-dimensional network based on FDTD [C]. Asia-Pacific Symposium on Electromagnetic Compatibility:920-923. |
| [6] | Dey S, Mittra R. 1998. A modified locally conformal finite-difference time-domain algorithm for modeling three-dimensional perfectly conducting objects [J]. Microwave and Optical Technology Letter, 17(6):349-352 |
| [7] | Li Q, Dong H, Tang W. 2003. A simplified CFDTD algorithm for scattering analysis [C]. 2003 6th International Symposium on Antennas and propagation and EM Proceedings, Beijing: 404-407. |
| [8] | MacGillivray J T. 2008. Trillion Cell CAD-Based Cartesian Mesh Generator for the Finite Difference Time Domain Method on a Single-Processor 4-GB Workstation [J].IEEE Transactions on Antennas and Propagation, 56(8):2187-2190. |
| [9] | MacGillivray J T. 2008. Trillion Cell CAD-Based Cartesian Mesh Generator for the Finite Difference Time Domain Method on a Single-Processor 4-GB Workstation [J].IEEE Transactions on Antennas and Propagation, 56(8):2187-2190. |
| [10] | Macinnes S C, Snyder D D, Zonge K L. 2002. Physics-based characterization of UXO from multi-component TEM data[C]. |
| [11] | Macinnes S C, Snyder D D, George D C, et al. 2002. Model-based UXO classification based on static 3-component TEM measurements[J]. SAGEEP 2002. |
| [12] | Oristaglio M L, Hohmann G W. 1984.Diffusion of electromagnetic fields into a two-dimensional earth: A finite-difference approach[J]. Geophysics. 49(7): 870-894. |
| [13] | RaiMittra, Wenhua Yu, Yongquan Lu, Rui Lu. 2008. GEMS-A General Purpose Conformal FDTD Solver Tailored for Parallel latforms[C]. Asia-Pacific Symposium on Electromagnetic Compatibility, 44-47. |
| [14] | Rai Mittra, Wenhua Yu, Yongquan Lu, Rui Lu. 2008. GEMS-A General Purpose Conformal FDTD Solver Tailored for Parallel Platforms[C]. Asia-Pacific Symposium on Electromagnetic Compatibility, 44-47. |
| [15] | Santos F A M, Perea H, Massoud U, et al. 2009. Using tensorial electrical resistivity survey to locate fault systems[J]. Journal of Geophysics and Engineering. 6(4): 390. |
| [16] | Smith R, Fountain D, Allard M. 2003. The MEGATEM fixed-wing transient EM system applied to mineral exploration: a discovery case history[J]. First Break. 21(7). |
| [17] | Srisukh Y, Nehrbass J, Teixeira F L, Lee J F, Lee R. 2003. Automatic grid generation of complex geometries for 3D FDTD simulations [C]. IEEE Antennas and Propagation Society International Symposium:326-329. |
| [18] | Srisukh Y, Nehrbass J, Teixeira F L, Lee J F, 2003. Lee R. Automatic grid generation of complex geometries for 3D FDTD simulations [C]. IEEE Antennas and Propagation Society International Symposium:326-329. |
| [19] | Wenhua Yu, Xiaoling Yang, Yongjun Liu, Rai Mittra. 2009. Electromagnetic Simulation Techniques Based on the FDTD Method [M].New Jersey: John Wiley & Sons. |
| [20] | Xiao T, Liu Q H. 2004.Enlarged cells for the conformal FDTD method to avoid the time step reduction [J]. IEEE Microwave and Wireless Components Letters, 14(12):551-553 |
| [21] | Yu W H, Mittra R. 2000. A conformal FDTD software package modeling antennas and microstrip circuit components [J]. IEEE Antennas and Propagation Magazine, 42(5):28-39. |
| [22] | Yu W, Mittra R. 2001. A conformal finite difference time domain technique for modeling curved dielectric surfaces [J]. IEEE Microwave and Wireless Components Letters, 11(1):25-27. |
| [23] | Zhang Y, Li L, Liang C H. 2002. A modified locally conformal FDTD method for broadwall radiating slot in a finite wall thickness waveguide [J]. Microwave and Optical Technology Letter. 35(3): 198-201 |
| [24] | Zivanovic S S, Yee K S, Mei K K. 1991. A Subgridding Method for the Time-domain Finite-difference method to solve Maxwell’s Equations [J]. IEEE Transactions on Microwave Theory and Techniques, 39(3): 471-479. |
| [25] | Xue G, Qin K, Li X, et al. 2012. Discovery of a large-scale porphyry molybdenum deposit in Tibet through a modified TEM exploration method[J]. Journal of Environmental & Engineering Geophysics. 17(1): 19-25. |
| [26] | Viezzoli A, Munday T, Auken E, et al. 2011. Accurate quasi 3D versus practical full 3D inversion of AEM data-the Bookpurnong case study[J]. Preview. 2010(149): 23-31. |
| [27] | 丁艳飞,白登海,许诚.2012.均匀半空间表面大定源瞬变电磁响应的快速算法[J].地球物理学报,06:2087-2096.doi:10.6038/j.issn.0001-5733.2012.06.030. |
| [28] | 孟庆鑫,潘和平.2012.地-井瞬变电磁响应特征数值模拟分析[J].地球物理学报,03:1046-1053.doi:10.6038.j.issn.0001-5733.2012.03.035 |
| [29] | 蒋大青,付志红,侯兴哲,等.2012.基于Maxwell 3D瞬变电磁法三维正演研究[J].电测与仪表, 06:29-32. |
| [30] | 王建,彭仲秋,谢处方.1996.地下目标瞬时散射的时域有限差分法数值模拟[J].地球物理学报,S1:349-356. |
| [31] | 戚志鹏,李貅,吴琼,等.2013.从瞬变电磁扩散场到拟地震波场的全时域反变换算法[J].地球物理学报,10:3581-3595.doi:10.6038./cjg2013033. |
| [32] | 齐彦福,殷长春,王若,等.2015.多通道瞬变电磁m序列全时正演模拟与反演[J].地球物理学报,07:2566-2577.doi:10.6038/cjg20150731. |
| [33] | 邱稚鹏,李展辉,李墩柱,等.2013.基于非正交网格的带地形三维瞬变电磁场模拟[J].地球物理学报,12:4245-4255.doi:10.6038/cjg20131227. |
| [34] | 卢绪山.2014.隧道TBM机瞬变电磁响应三维并行模拟及干扰去除研究[D].长安大学. |
| [35] | 孙怀凤,李貅,李术才,等.2013.考虑关断时间的回线源激发TEM三维时域有限差分正演[J].地球物理学报.03: 1049-1064.doi:10.6038/cjg20130333. |
| [36] | 孙怀凤.2013.隧道含水构造三维瞬变电磁场响应特征及突水灾害源预报研究[D].山东大学 |
| [37] | 宋汐瑾,党瑞荣,郭宝龙,等.2011.井中磁源瞬变电磁响应特征研究[J].地球物理学报,04:1122-1129.doi:10.3969/j.issn.0001-5733.2011.04.028. |
| [38] | 汤井田,公劲喆.2010.基于GiD的有限元前处理和后处理可视化[J].地球物理学展01:186-195. doi:10.3969/j.issn.1004-2903.2010.01.026. |
| [39] | 李貅.2002.瞬变电磁测深的理论与应用[M].西安:陕西科学技术出版社. |
| [40] | 李貅,武军杰,曹大明,等.2006.一种隧道水体不良地质体超前地质预报方法—瞬变电磁法[J].工程勘察,03:70-75. |
| [41] | 李貅,张莹莹,卢绪山,等.2015.电性源瞬变电磁地空逆合成孔径成像[J].地球物理学报,01:277-288.doi:10.6038/cjg20150125. |
| [42] | 李貅,刘文韬,智庆全,等.2015.核磁共振与瞬变电磁三维联合解释方法[J].地球物理学报,08:2730-2744.doi:10.6038/cjg20150810. |
| [43] | 李建慧,胡祥云,曾思红,等.2013.基于电场Helmholtz方程的回线源瞬变电磁法三维正演[J].地球物理学报,12:4256-4267.doi:10.6038/cjg20131228. |
| [44] | 李建慧,朱自强,曾思红,等.2012.瞬变电磁法正演计算进展[J].地球物理学进展,2012,04:1393- 1400.doi:10.6038/j.issn.1004-2903.2012.04.013. |
| [45] | 李展辉,黄清华.2014.复频率参数完全匹配层吸收边界在瞬变电磁法正演中的应用[J].地球物理学报,04:1292-1299.doi:10.6038/cjg20140426. |
| [46] | 李静,曾昭发,吴丰收,等.2010.探地雷达三维高阶时域有限差分法模拟研究[J].地球物理学报,04:974-981.doi:10.3969/j.issn.0001-5733.2010.04.022. |
| [47] | 李向军,马秋华,焦景欣,等.2008.基于通用CAD几何模型的复杂目标 RCS 计算[J]. 探测与控制学报, 30(6):46-50. |
| [48] | 李迎春,徐果明,徐涛.2002.地下介质三维模型中界面的描述方法.地球物理学进展, 17(3): 445- 450 |
| [49] | 王建,彭仲秋,谢处方.1996.地下目标瞬时散射的时域有限差分法数值模拟[J]. 地球物理学报S1:349-356. |
| [50] | 王帮兵,田钢,孙波,等.2009.南极冰盖内部结构特性研究—基于三维各向异性电磁波时域有限差分方法[J]. 地球物理学报, 04:966-975. |
| [51] | 王华军,罗延钟.2003.中心回线瞬变电磁法2.5维有限单元算法[J].地球物理学报,06:855-862. |
| [52] | 王祎鹏.2014.大回线源瞬变电磁法全域视电阻率定义研究[D].长安大学. |
| [53] | 徐涛,徐果明,高尔根,等.2004.三维复杂介质的块状建模和试射射线追踪[J]. 地球物理学报,06:1118-1126. |
| [54] | 熊彬,罗延钟.2006.电导率分块均匀的瞬变电磁2.5维有限元数值模拟[J]. 地球物理学报,02:590-597. |
| [55] | 薛国强,李貅.2008.瞬变电磁隧道超前预报成像技术[J].地球物理学报,03:894-900. |
| [56] | 许洋铖,林君,李肃义,等.2012.全波形时间域航空电磁响应三维有限差分数值计算[J].地球物理学报,06:2105-2114.doi:10.6038/j.issn.0001-5733.2012.06.032. |
| [57] | 殷长春,刘斌.1994.瞬变电磁法三维问题正演及激电效应特征研究[J].地球物理学报,S2:486-492. |
| [58] | 殷长春,黄威,贲放.2013.时间域航空电磁系统瞬变全时响应正演模拟[J].地球物理学报,09:3153-3162. |
| [59] | 闫玉波,石守元,葛德彪.1998.用于FDTD的复杂目标建模[J].西安电子科技大学学报, 25(3): 389-392. |
| [60] | 杨长春,冷传波,李幼铭.1997.适于复杂地质模型的三维射线追踪方法.地球物理学报, 40(3): 414- 420. |
| [61] | 岳建华,杨海燕,胡搏.2007.矿井瞬变电磁法三维时域有限差分数值模拟[J]. 地球物理学进展, 06:1904-1909. |
| [62] | 杨守文,汪宏年,陈桂波,等.2009.倾斜各向异性地层中多分量电磁波测井响应三维时域有限差分(FDTD)算法[J].地球物理学报03:833-841. |
| [63] | 张保祥,刘春华.2004.瞬变电磁法在地下水勘查中的应用综述[J].地球物理学进展,03:537-542. |
| [64] | 张开元,韩自豪,周韬.2007.瞬变电磁法在探测煤矿采空区中的应用[J].工程地球物理学报,04:341-344. |
| [65] | 张世田,任小红,杨利霞,等.2011.基于FDTD的目标双站RCS计算方法及其应用[J].微波学报,27(3):5-8. |
| [66] | 张军,赵莹,李萍.2012.矿井瞬变电磁法在超前探测中的应用研究[J]. 工程地球物理学报,01:49-53. |
 2015, Vol. 30
2015, Vol. 30


