天然气水合物在全球清洁能源替代以及温室效应、海底滑塌等自然灾害预防等研究方面具有重要影响.海底天然气水合物储层的厚度通常较薄(<40 m),常规地震勘探技术很难达到要求.据杨睿等(2013)不完全统计,全球85处海域天然气产地中未发现明显似海底反射层(BSR)标志的有18处,约占21%,水合物的存在与BSR并非严格对应.在无明显BSR标志区域,如何识别天然气水合物将成为研究难点.对于深水勘探,受数据获取成本限制,能直接用于水合物评价或地震约束反演的测井资料极少.全波形反演(Full Waveform Inversion,FWI)以全波场模拟为基础,充分利用地震波场包含的地下岩性与流体细节变化信息,可以在无井或少井区域求取高分辨率水合物沉积层速度结构,该方法已被广泛应用于大陆边缘天然气水合物勘探研究中(Singh et al.,1993; Minshull et al.,1994; Pecher et al.,1996; Korenaga et al.,1997; Yuan et al.,1999; 宋海斌等,2003).
20世纪80年代,Tarantola(1984a,1984b,1986,1988)发表了一系列关于地震波场反演的论文,奠定了全波形反演理论基础,Kolb等(1986)和Gauthier等(1986)用理论模型合成数据进行声波全波形反演测试,Mora(1987)对复杂模型实现了弹性波全波形反演,展示了全波形反演的潜力,并指出反演结果严重依赖于初始模型.(Pratt and Worthington 1990; Pratt,1990)将频率域正演模拟和Tarantola全波形反演的思想相结合,发展了频率域声波和弹性波全波形反演,Shin和Cha(2008,2009)提出了Laplace域全波形反演.近年来,Virieux和Operto(2009)对全波形反演的研究现状做了全面概述,并指出所面临的挑战.全波形反演在国内的研究相对滞后,许琨和王妙月(2001,2004)先后给出了基于有限元模拟的声波和弹性波全波形反演.高凤霞等(2013)详细对比了频率域中几种优化方法的收敛速度、计算存储量以及算法稳定性,为后续多参数反演提供参考.卞爱飞(2011)从阻尼因子与阻尼信号角度出发,建立时间域和频率域阻尼波动方程,指出常规频率域波动方程、考虑常Q值衰减效应的频率域波动方程以及Laplace域波动方程都是频率域阻尼波动方程的特例,可以利用频率域阻尼波动方程代替其他三种方程进行波场正演与反演研究,并提出阻尼剥层波形反演法与多尺度剥层波形反演流程.杨积忠等(2014)从变密度声波方程出发,在分析各参数之间相互影响基础上提出了一种速度、密度多参数全波形反演策略,其采用分步反演,将第一步反演结果中相对可靠的速度作为下一步反演初始速度模型,在一定程度上降低了多参数反演的非线性程度.另外,卞爱飞等(2010)和杨午阳等(2013)分别对国内外全波形反演研究进展做了详细总结.
全波形反演利用完整波形信息特别是将振幅信息参与反演,这是该方法具有高分辨率反演结果的根本原因,对于诸如盐丘等复杂构造,全波形反演方法的速度建模能力已经得到理论模型检验(Choi et al.,2008; Li et al.,2013).本世纪以来,随着高性能计算平台技术的快速发展,全波形反演正逐步应用于实际地震资料中,其在海洋多分量地震数据(Delescluse et al.,2011)、井间地震资料(Zhou and Greenhalgh,2003; Ernst et al.,2007; Marelli et al.,2012)以及时移地震数据(Watanabe et al.,2004; Lambot et al.,2009; Queiβer and Singh,2013)等研究中均取得一定效果.
1 水合物参数结构分析研究进展Singh和Minshull(1993)首次将全波形反演应用于天然气水合物勘探中,预测出加拿大温哥华岛近海卡斯卡底(Cascadia)边缘似海底反射层下方游离气的存在以及厚度,该实验结果得到大洋钻探第146航次证明(MacKay et al.,1994; Singh and Minshull,1994).Korenaga等(1997)对布莱克(Blake)海脊地区的宽方位角地震数据进行全波形反演研究,通过分析BSR附近速度结构变化指出该地区水合物的存在,进而对该地区水合物生成的控制因素做了分析.Watanabe等(2004)对加拿大麦肯锡(Mallik)三角洲地区时移井间地震数据进行全波形反演,成功检测出高速水合物开采后的低速游离气圈闭区域,其结果由测井数据所验证,在实验中,虽然低速开采区域范围很小,但全波形反演依然可以有效识别,进一步体现了全波形反演高精度优势.另外,在印度克里希纳-戈达瓦里(Krishna-Godavari)盆地(Jaiswal et al.,2012)、新西兰希库朗伊(Hikurangi)边缘(Crutchley et al.,2011)、巴基斯坦麦克兰(Makran)海岸地区(Sain et al.,2000)以及挪威西北斯瓦尔巴群岛(Svalbard)大陆边缘(Westbrook et al.,2008)等地区水合物研究中,全波形反演同样发挥了重要作用,为海域缺乏测井等资料情况下水合物研究提供了一种可靠方法.
我国天然气水合物调查研究起步稍晚,宋海斌(2003)首次将全波形反演应用于日本东南海(Nankai)海槽双BSR速度结构研究中,为水合物与游离气分布特征研究提供了有力依据.Huo和Zhang(2009)将全波形反演应用于我国南海北部天然气水合物研究中,得到高分辨率BSR速度结构,其反演思路基本与Singh所采用的方法类似,反演全局优化算法采用遗传算法,提高了传统波形反演计算效率.Sun等(2012)采用全波形反演对中国南海珠江口盆地白云凹陷BSR速度结构做了分析,并详细研究了与水合物运移密切相关的“气烟囱”构造,为分析水合物成藏系统提供可靠依据.
实验证明(Yuan et al.,1999),天然气水合物和游离气都可以引起AVO异常,因此AVO技术广泛应用于水合物研究中(Katzman et al.,1994; Andreassen et al.,1997; Carcione and Tinivella,2000; Tinivella and Accaino,2000; 宋海斌等,2002),但其有效性仍存在争议,其争议体现在:(1)水合物储层具有多个薄互层相间的特点,因此产生的多次反射以及干涉调谐效应会很大程度上影响AVO分析准确度;(2)在应用AVO异常来估算游离气饱和度时,1%的饱和度就可引起明显的AVO异常,饱和度超过2%以后,增量对异常影响很小(Andreassen et al.,1997),因此很难利用单一AVO技术来预测游离气饱和度准确值.AVO分析只利用了波形信息中的最大振幅,上世纪90年代初期Dahl等(Dahl and Ursin,1991)将AVO分析与波形反演的思想相结合,形成了AVO多参数波形反演方法,可以降低薄层效应的影响,提高信息利用率.但是由于饱和度与弹性参数岩石物理关系还不是很明确,因此全波形反演在水合物饱和度预测应用的准确度还有待考证.
2 天然气水合物全波形反演策略 2.1 水合物正演模拟方法地震波场数值模拟主要分为基于运动学特征的射线追踪法和基于动力学特征的波动方程法,其中波动方程法又分为有限差分法、有限元法、伪谱法和反射率法等.射线追踪法由于将地震波波动理论简化为以惠更斯原理和斯奈尔定理为基础的射线理论,计算效率高,在发展初期计算机处理能力有限情况下广泛使用,但是没有考虑地震波动力学特征,容易受薄层多次反射波和转换波影响,因此将该方法应用于叠前全波形反演无法满足精度要求.有限差分和有限元可以准确的模拟层间多次波和转换波,且能很好反应横向非均匀介质特征,但计算量大.
反射率法通常利用Kennett广义反射透射系数矩阵递推(Kennett,1979,1980)以及平面波分解和合成来实现地震波模拟,该方法可以有效模拟多次波以及转换波波形,较有限差分法或有限元法计算效率高,是水平层状天然气水合物全波场模拟的理想方法.在研究早期,全波形反演在水合物勘探中应用主要是分析与海底平行的BSR附近速度结构,研究区域大多为水平层状结构,因此反射率法被广泛采用(Minshull et al.,1994; Yuan et al.,1996; Pecher et al.,1996,1998; Korenaga et al.,1997; Xia et al.,1998; Mallick et al.,2000).
但反射率法受地质模型为近似水平层状条件限制,对于复杂构造区域,输入数据必须先经过叠前时间偏移甚至叠前深度偏移,鉴于目前深度偏移技术还有待改进,因此反射率法并不能满足复杂地质区域天然气水合物全波形反演的要求.随着计算机计算能力的飞速发展,一些学者开始将有限差分正演模拟方法应用到水合物全波形反演中,Barnes和Noble(2007)在对日本南海海槽水合物研究中,采用时间域交错网格有限差分正演模拟方法,而Pratt等(2003)则将频率域有限差分应用到加拿大麦肯锡三角洲地区水合物研究中,同样在印度克里希纳-戈达瓦里盆地水合物研究中,Jaiswal(2012)也采用频率域有限差分模拟方法,实现了纵波速度和衰减系数联合反演.由于有限元正演模拟要求更高的计算量,因此现阶段应用比较少,近年来,Kim等(2013)首次将有限元弹性波模拟应用于水合物全波形反演研究中,该方法采用声波-弹性波耦合波动方程(Kim et al.,2009),实现横波速度的反演.
2.2 水合物全波形反演方法Singh和Minshull(1993)首次将全波形反演应用于海域天然气水合物勘探中,其采用方法可以归结为“降维”与“尺度分解”相结合的反演策略:降维体现在该方法基于层状介质假设;尺度分解指利用同相轴走时信息全局优化获取速度长波长或背景速度,利用完整波形信息获取速度短波长分量.Singh等(1991,1993)采用Monte-Carlo搜索来寻找全局最优,该随机搜索方法可以避免梯度法易陷入局部极小值的缺点,但搜索方向完全随机,这样在多参数同时反演时效率太低.这一策略在水合物应用早期极具代表性,该方法能够有效计算BSR附近水合物和游离气速度结构,被广泛应用于大陆边缘天然气水合物勘探中,如南美哥伦比亚西海岸(Minshull et al.,1994)、秘鲁近海岸(Pecher et al.,1996)、太平洋卡斯卡底古陆边缘(Yuan et al.,1996)、布莱克海台与加利福尼亚隆起(Korenaga et al.,1997)、哥斯达黎加(Costa Rican)岸外汇聚型大陆边缘(Pecher et al.,1998)、巴基斯坦麦克兰海岸(Sain et al.,1998)、日本南海海槽(宋海斌等,2003)、挪威西北斯瓦尔巴群岛大陆边缘(Westbrook et al.,2008),中国南海北部海域(霍元媛和张明,2010),新西兰希库朗伊大陆边缘(Crutchley et al.,2011)等.
Xia等(1998)提出了一种基于分治算法的全波形反演方法,并将该方法应用于美国东海岸卡罗莱纳(Carolina)海槽(Xia et al.,2000),该方法主要步骤为:(1)首先采用快速模拟退火法来求取速度的低频背景分量;(2)然后采用基于近似线性反射系数的AVO反演来获取平滑背景速度的高频扰动分量;(3)最后将低频背景速度分量和高频扰动速度分量相结合构成全波形反演的初始速度模型,从而应用全波形反演来获取BSR附近沉积层速度结构以及游离气、水合物厚度等信息.由于此方法采用的初始速度模型和真实速度模型很接近,因此可以将最后的反演看作是似线性问题来解决.快速模拟退火法(Very Fast Simulated Annealing,VFSA)由Ingber(1989)提出,其不同于模拟退火法,更新模型是根据当前模型温度的柯西分布所推导而来,这样当温度升高时可以增加采样数,而温度降低时则缩小采样数,另外每个模型参数都有独立的退火准则和模型空间采样准则,因此可以独立控制每个参数并且和先验信息相统一,加快收敛速度.同样,宋海斌(2003)在对日本东南海海槽BSR速度结构研究中也采用快速模拟退火法来求取速度长波长分量.
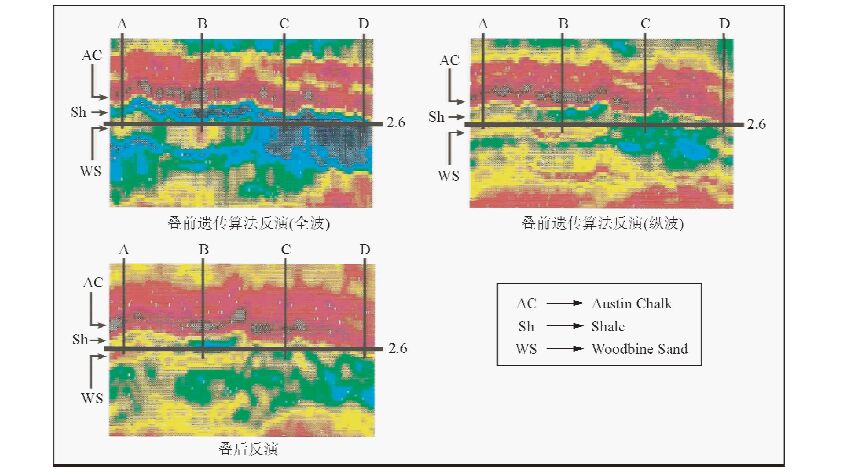
Mallick(1999)提出一种基于遗传算法的全波形反演方法,该算法将叠加角道集数据与叠前资料结合,弥补了叠前资料覆盖次数低的不足.其将该方法应用于东德克萨斯州含气砂岩地区实际资料中,并结合井资料和实际生产数据证明基于遗传算法的叠前全波形反演较叠后反演能够更详细的刻画地层信息,并且可以区分由于转换波和多次反射波所引起的虚假AVO异常,处理调谐效应.另外,Mallick指出虽然忽略转换波和多次波可以提高计算速度,但是,Woodbine地区含气砂岩实验表明包含P波、转换波以及多次波的全波反演比采用单一P波反射能量的反演可以更准确获取薄层含气砂岩信息(图 1).
|
图 1 叠前遗传算法全波反演、仅使用P波反射能量的叠前遗传算法反演以及叠后反演的结果对比(Mallick,1999) Fig. 1 A comparison of prestack GA inversion that computed a complete elastic response with prestack GA inversion with P-wave primary reflection energy only,and with poststack inversion(Mallick,1999) |
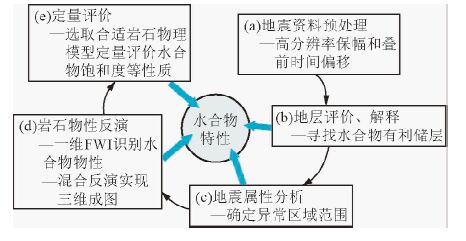
随后,Mallick(2000)将该叠前遗传算法全波形反演与叠后反演相结合提出一种叠前叠后混合的反演方法.在整个反演过程中,由于叠前全波形反演可以在缺乏井资料的情况下提供低频纵、横波波阻抗趋势,避免调谐效应,很适合深海天然气水合物勘探,该优点通过实际资料得到证明.另外,一维叠前全波形反演和三维叠后反演相结合既避免了无井约束下叠后反演的多解性,也解决了叠前全波形反演计算量大的问题,提供了一种可行、快速三维反演成图思路.Dai等(2004,2008)将该技术与地震地层学原理以及Dvorkin等(2003)提出的天然气水合物岩石物理模型相结合开发了一套完整的“天然气水合物地震勘探五步法流程”(图 2),并对墨西哥湾水合物沉积层速度结构以及饱和度做了详细评估.随着高信噪比和宽频地震技术的发展,该方法逐渐变得可行.需要指出的是该方法虽然采用三维地震数据,但是叠前全波形反演仍局限于一维,水合物饱和度预测是基于三维叠后反演结果所实现的,其主要受制于三维叠前全波形反演的巨大计算量.
|
图 2 天然气水合物地震勘探五步法流程 (Dai et al.,2004) Fig. 2 The five-step process for gas hydrate detection and estimation using seismic data(Dai et al.,2004) |
上述分步法水合物全波形反演方法基于层状介质假设,认为BSR附近速度结构为层状或似层状,为了考虑水合物物性参数的强横向变化,一些学者采用直接反演方法来获取水合物区域速度、密度以及衰减系数等物性参数.Barnes和Noble(2007)采用二维时间域全波形反演方法,正演模拟采用有限差分法,对日本南海海槽实际数据实验证明,该方法具有很强的鲁棒性,可以得到可靠纵波速度.Pratt等(2003)采用频率域全波形反演技术,对加拿大麦肯锡三角洲地区水合物分布区域速度和品质因子进行反演重建,得到更加详细的水合物分布情况,再次印证了“高速层区域具有低品质因子”的假设.Jaiswal等(2012)将频率域全波形反演应用于印度克里希纳-戈达瓦里盆地中,实现纵波速度VP和纵波衰减系数QP-1联合反演,证明该地区水合物分布受构造和地层的双重控制.Kim等(2013)将以有限元弹性波模拟(Kim et al.,2009)为基础的全波形反演应用于日本和韩国之间郁陵(Ulleung)盆地水合物勘探中,正演采用声波-弹性波耦合波动方程(Komatitsch et al.,2000),得到纵横波速度、密度以及泊松比,为水合物勘探提供更多岩性信息.
3 关键技术探讨 3.1 地震子波估计方式前期天然气水合物全波形反演中,一些研究者通过海底首次反射和全程多次波的反褶积来估计震源子波(Minshull et al.,1994; Pecher et al.,1996; Korenaga et al.,1997;Sain et al.,2000),其假设海底子波为震源子波与反射系数褶积.Yuan等(1999)认为确定震源子波后海底反射在大多数情况下是单一对称零相位脉冲,并且可以将海底近似看做密度和速度分界面,因此通过利用近偏移距数据来产生规则震源子波是比较合理的.Pecher等(1998)详细讨论了子波对反演结果的影响,指出震源子波估计的一点误差就可能引起海底很大的速度变化,降低BSR附近水合物层速度预测精度.Xia等(1998)认为应该将子波作为反演的一部分,而不是固定不变.
Chikichev等(2012)提出了一种基于一次反射波和多次反射波的震源子波提取方法,该方法通过一次反射波的全波形反演来获得初始模型,然后利用初始模型模拟多次波,最后将模拟多次波与实际地震记录对比匹配来不断修正子波.实验表明,该方法在子波相位发生变化时仍可以实现一次波和多次波的同时匹配,避免了子波相位不准确所带来的反演误差.而且该方法不依赖井控调整子波,很适合深海水合物勘探井资料缺乏的情况,当然该方法是否能成功应用到BSR以及周围水合物速度结构分析中还有待研究.
3.2 海底多分量地震数据早期海域天然气水合物勘探中只能获取纵波信息,然后通过经验公式来得到横波速度,无法满足精确预测水合物饱和度的要求.目前,海洋地震调查技术发展迅速,深海拖曳地震技术、海底多分量地震调查技术、广角地震反射技术等逐渐成熟.海底多分量地震勘探技术可以直接获取横波信息,还可以很好避免多次波和面波干扰.Backus等(2006)将海底多分量地震勘探技术应用于墨西哥湾水合物调查中,成功获取PS转换波信息,提高了水合物预测的精度.同样海底地震仪(OBS)也可以获取精确的地震数据,Westbrook等(2008)在对挪威西北斯瓦尔巴群岛大陆边缘等地区水合物全波形反演研究中,采用OBS多分量地震数据对水合物沉积层纵横波速度结构进行高精度成像,进而预测水合物饱和度等岩石物理性质.最近,张光学等(2014)以三维高分辨率地震与海底高频地震仪联合勘探数据为基础,获取我国南海神狐海域某区域天然气水合物沉积层纵、横波速度结构,其纵波速度下降但横波速度变化较小特征可能预示游离气的存在.
3.3 多参数同时反演早期水合物全波形反演中,Singh等(1993)、Pecher等(1996)、宋海滨等(2003)、Huo和Zhang(2009)等学者仅将纵波速度作为反演参数来实现,对于横波速度以及密度等参数则采用经验公式来获得.一般通过Hamilton关系(Hamilton,1978)求出密度,采用浅海沉积中简单的纵横波速度经验关系(Castagna et al.,1985)求出横波,将纵横波品质因子Q值则设置为固定值,例如Minshull等(1994)将沉积层QP设置为100,QS设置为25,甚至有些并未考虑衰减系数对反演结果的影响(Barnes and Noble,2007),反演结果存在不确定性,因此很有必要发展多参数水合物全波形反演方法.
和纵波速度一样,纵波衰减系数(QP-1)也是判断水合物分布重要的物性参数(Cordon et al.,2006).目前,水合物衰减系数的机理还不是很明确(Pecher and Holbrook,2003; Priest et al.,2006; Gerner et al.,2007; Rossi et al.,2007),因此对于衰减系数的反演研究比较少.Pratt等(2003)在对加拿大麦肯锡三角洲地区水合物研究中对速度和Q值进行全波形反演重建,为预测水合物饱和度提供了有力工具,再次证明“高速层区域具有低品质因子”的假设.同样,Jaiswal等(2012)在对印度克里希纳-戈达瓦里盆地水合物研究中,对VP与QP-1进行联合反演,表明游离气对衰减有增强作用,而水合物则会抑制衰减.
各向异性参数的全波形反演可以说是研究中最具有挑战性的领域之一,具有垂直对称轴的横向各向同性(VTI)介质和具有倾斜对称轴的横向各向同性(TTI)介质在油气勘探中通常被认为是真实地质介质的体现.在VTI介质中,正常时差(NMO)纵波速度只决定于两个参数:水平层反射的NMO速度VNMO(0)=VP$\sqrt {1 + 2\delta } $和η=(ε-δ)/(1+2δ)参数(Alkhalifah and Tsvankin,1995),η为Thomsen参数(Thomsen,1986)δ和ε的结合.Barnes和Noble(2007)给出了时间域水合物各向异性全波形反演的可行性研究,将参数分为五类:VP,VS,density,δ和ε,实现每类参数的反演重建.
4 结束语4.1 随着计算机速度的加快以及宽孔径和宽方位观测系统的发展,三维声波FWI如今已经可以实现.但大部分三维应用局限在低频段(<7 Hz)(Plessix,2009),FWI可以看作是一个速度模型反演重建的工具.在三维FWI情况下,多炮正演模拟效率是主要关注点之一.近年来,Krebs等(2009)和Ben-Hadj-Ali等(2009)将震源组合和相位编码技术分别应用于时间域和频率域全波形反演,有效降低了计算量,使三维全波形反演的实际应用逐渐成为可能.可以预见,在天然气水合物探测中,三维资料的全波形反演将是下一个突破方向.
4.2 近年来,Shin和Cha(2008)提出了Laplace域声波波形反演方法,该方法通过对取对数后的波场低频部分进行最小二乘拟合可以在低频成分缺失的情况下恢复长波长速度分量,为时间域或频率域波形反演提供可靠的初始速度模型.特别是在类似SEG/EAGE模型强速度差异的情况下,结合长偏移距地震数据,该方法能有效提供正确背景速度模型(Pyun et al.,2008),避免层间多次波和转换波影响,具有很强的稳健性(Ha and Shin,2013).由于频率域波形反演可以更多描述速度的高频细节部分,因此Shin和Cha(2009)将二者相结合建立了Laplace-Fourier域混合波形反演方法,并将其应用于不规则地表条件下的声波-弹性波耦合介质,适合海域水合物勘探情况.目前,仍未见到Laplace-Fourier域波形反演在海域天然气水合物中的应用,该方法是否能够有效重建水合物沉积层精细速度结构还有待验证.
致 谢 感谢审稿专家和编辑部老师的耐心指导和帮助.
| [1] | Alkhalifah T, Tsvankin I. 1995. Velocity analysis for transversely isotropic media[J]. Geophysics, 60(5): 1550-1566. |
| [2] | Andreassen K, Hart P E, MacKay M. 1997. Amplitude versus offset modeling of the bottom simulating reflection associated with submarine gas hydrates[J]. Marine Geology, 137(1-2): 25-40. |
| [3] | Backus M M, Murray P E, Hardage B A, et al. 2006. High-resolution multicomponent seismic imaging of deepwater gas-hydrate systems[J]. The Leading Edge, 25(5): 578-596. |
| [4] | Barnes C, Noble M. 2007. Feasibility study to quantify gas hydrates using an anisotropic full waveform inversion in the time domain[C].// 77th Annual International Meeting, Society of Exploration Geophysicists, Expanded Abstracts, 1825-1829. |
| [5] | Ben-Hadj-Ali H, Operto S, Virieux J. 2009. Three-dimensional frequency-domain full waveform inversion with phase encoding[C]. // 79th Annual International Meeting, Society of Exploration Geophysicists, Expanded Abstracts, 2288-2292. |
| [6] | Bian A F. 2011. Theory and application of full waveform inversion in reflection seismology (in Chinese)[Ph. D. thesis]. Wuhan: China University of Geosciences (Wuhan). |
| [7] | Bian A F, Yu W H, Zhou H W. 2010. Progress in the frequency-domain full waveform inversion method[J]. Progress in Geophysics (in Chinese), 25(3): 982-993, doi: 10.3969/j.issn.1004-2903.2010.03.037. |
| [8] | Carcione J M, Tinivella U. 2000. Bottom-simulating reflectors: Seismic velocities and AVO effects[J]. Geophysics, 65(1): 54-67. |
| [9] | Castagna J P, Batzle M L, Eastwood R L. 1985. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks[J]. Geophysics, 50(4): 571-581. |
| [10] | Chikichev I, Wang K, Lazaratos S. 2012. Wavelet estimation and multiple modeling in full-waveform inversion[C]. // 74th EAGE Conference & Exhibition-Workshops. |
| [11] | Choi Y, Min D, Shin C. 2008. Frequency-domain elastic full waveform inversion using the new pseudo-Hessian matrix: Experience of elastic Marmousi-2 synthetic data[J]. Bulletin of the Seismological Society of America, 98(5): 2402-2415. |
| [12] | Cordon I, Dvorkin J, Mavko G. 2006. Seismic reflections of gas hydrate from perturbational forward modeling[J]. Geophysics, 71(6): F165-F171. |
| [13] | Crutchley G J, Gorman A R, Pecher I A, et al. 2011. Geological controls on focused fluid flow through the gas hydrate stability zone on the southern Hikurangi Margin of New Zealand, evidenced from multi-channel seismic data[J]. Marine and Petroleum Geology, 28(10): 1915-1931. |
| [14] | Dahl T, Ursin B. 1991. Parameter estimation in a one-dimensional anelastic medium[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 96(B12): 20217-20233. |
| [15] | Dai J C, Snyder F, Gillespie D, et al. 2008. Exploration for gas hydrates in the deepwater, northern Gulf of Mexico: Part I. A seismic approach based on geologic model, inversion, and rock physics principles[J]. Marine and Petroleum Geology, 25(9): 830-844. |
| [16] | Dai J C, Xu H B, Snyder F, et al. 2004. Detection and estimation of gas hydrates using rock physics and seismic inversion: Examples from the northern deepwater Gulf of Mexico[J]. The Leading Edge, 23(1): 60-66. |
| [17] | Delescluse M, Nedimovic' M R, Louden K E. 2011. 2D waveform tomography applied to long-streamer MCS data from the Scotian Slope[J]. Geophysics, 76(4): B151-B163. |
| [18] | Dvorkin J, Nur A, Uden R, et al. 2003. Rock physics of a gas hydrate reservoir[J]. The Leading Edge, 22(9): 842-847. |
| [19] | Ernst J R, Green A G, Maurer H, et al. 2007. Application of a new 2D time-domain full-waveform inversion scheme to crosshole radar data[J]. Geophysics, 72(5): J53-J64. |
| [20] | Gao F X, Liu C, Feng X, et al. 2013. Comparison and analyses of several optimization methods in the application of frequency-domain full waveform inversion[J]. Progress in Geophysics (in Chinese), 28(4): 2060-2068, doi: 10.6038/pg20130450. |
| [21] | Gauthier O, Virieux J, Tarantola A. 1986. Two-dimensional nonlinear inversion of seismic waveforms: Numerical results[J]. Geophysics, 51(7): 1387-1403. |
| [22] | Gerner A, Saenger E H, Shapiro S A. 2007. Attenuation of P-waves due to interlayer fluid flow in hydrate-bearing sediments[J]. Journal of Geophysics and Engineering, 4(4): 394. |
| [23] | Ha W, Shin C. 2013. Why do Laplace-domain waveform inversions yield long-wavelength results?[J]. Geophysics, 78(4): R167-R173. |
| [24] | Hamilton E L. 1978. Sound velocity-density relations in sea-floor sediments and rocks[J]. The Journal of the Acoustical Society of America, 63(2): 366-377. |
| [25] | Huo Y Y, Zhang M. 2009. Full waveform inversion of gas hydrate reflectors in Northern South China Sea[J]. Acta Geophysica, 57(3): 716-727. |
| [26] | Huo Y Y, Zhang M. 2010. The genetic algorithm based velocity structure waveform inversion for gas hydrate bottom simulating reflectors (BSR)[J]. Oil Geophysical Prospecting (in Chinese), 45(1): 55-59. |
| [27] | Ingber L. 1989. Very fast simulated re-annealing[J]. Mathematical and Computer Modelling, 12(8): 967-973. |
| [28] | Jaiswal P, Dewangan P, Ramprasad T, et al. 2012. Seismic characterization of hydrates in faulted, fine-grained sediments of Krishna-Godavari Basin: Full waveform inversion[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 117(B10), doi: 10.1029/2012JB009201. |
| [29] | Katzman R, Holbrook W S, Paull C K. 1994. Combined vertical-incidence and wide-angle seismic study of a gas hydrate zone, Blake Ridge[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 99(B9): 17975-17995. |
| [30] | Kennett B L N. 1979. Theoretical reflection seismograms for elastic media[J]. Geophysical Prospecting, 27(2): 301-321. |
| [31] | Kennett B L N. 1980. Seismic waves in a stratified half space-II. Theoretical seismograms[J].Geophysical Journal International, 61(1): 1-10. |
| [32] | Kim H J, Jou H T, Kang S G, et al. 2013. Seismic characterization and imaging of a gas hydrate deposit in the western part of the Ulleung Basin, the East Sea (Japan Sea)[J]. Marine and Petroleum Geology, 47: 214-221. |
| [33] | Kim M H, Choi Y, Cha Y H, et al. 2009. 2-D frequency-domain waveform inversion of coupled acoustic-elastic media with an irregular interface[J]. Pure and Applied Geophysics, 166(12): 1967-1985. |
| [34] | Kolb P, Collino F, Lailly P. 1986. Pre-stack inversion of a 1-D medium[J]. Proceedings of the IEEE, 74(3): 498-508. |
| [35] | Komatitsch D, Barnes C, Tromp J. 2000. Wave propagation near a fluid-solid interface:A spectral-element approach[J].Geophysics, 65(2): 623-631. |
| [36] | Korenaga J, Holbrook W S, Singh S C, et al. 1997. Natural gas hydrates on the southeast U.S. margin: Constraints from full waveform and travel time inversions of wide-angle seismic data[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 102(B7): 15345-15365. |
| [37] | Krebs J R, Anderson J E, Hinkley D, et al. 2009. Fast full-wavefield seismic inversion using encoded sources[J]. Geophysics, 74(6): WCC177-WCC188. |
| [38] | Lambot S, Slob E, Rhebergen J, et al. 2009. Remote estimation of the hydraulic properties of a sand using full-waveform integrated hydrogeophysical inversion of time-lapse, off-ground GPR data[J]. Vadose Zone Journal, 8(3): 743-754. |
| [39] | Li M K, Rickett J, Abubakar A. 2013. Application of the variable projection scheme for frequency-domain full-waveform inversion[J]. Geophysics, 78(6): R249-R257. |
| [40] | MacKay M E, Jarrard R D, Westbrook G K, et al. 1994. Origin of bottom-simulating reflectors: geophysical evidence from the Cascadia accretionary prism[J]. Geology, 22(5): 459-462. |
| [41] | Mallick S. 1999. Some practical aspects of prestack waveform inversion using a genetic algorithm: An example from the east Texas Woodbine gas sand[J]. Geophysics, 64(2): 326-336. |
| [42] | Mallick S, Huang X, Lauve J, et al. 2000. Hybrid seismic inversion: A reconnaissance tool for deepwater exploration[J]. The Leading Edge, 19(11): 1230-1237. |
| [43] | Marellik S, Maurer H, Manukyan E. 2012. Validity of the acoustic approximation in full-waveform seismic crosshole tomography[J]. Geophysics, 77(3): R129-R139. |
| [44] | Minshull T A, Singh S C, Westbrook G K. 1994. Seismic velocity structure at a gas hydrate reflector, offshore western Colombia, from full waveform inversion[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 99(B3): 4715-4734. |
| [45] | Mora P. 1987. Nonlinear two-dimensional elastic inversion of multioffset seismic data[J]. Geophysics, 52(9): 1211-1228. |
| [46] | Pecher I A, Minshull T A, Singh S C, et al. 1996. Velocity structure of a bottom simulating reflector offshore Peru: Results from full waveform inversion[J]. Earth and Planetary Science Letters, 139(3-4): 459-469. |
| [47] | Pecher I A, Ranero C R, Von Huene R, et al. 1998. The nature and distribution of bottom simulating reflectors at the Costa Rican convergent margin[J]. Geophysical Journal International, 133(2): 219-229. |
| [48] | Pecher I A, Holbrook W S. 2003. Seismic methods for detecting and quantifying marine methane hydrate/free gas reservoirs[A]. // Max M D ed. Natural Gas Hydrate[M]. Amsterdam: Springer Netherlands, 275-294. |
| [49] | Plessix R. 2009. Three-dimensional frequency-domain full-waveform inversion with an iterative solver[J]. Geophysics, 74(6): WCC149-WCC157. |
| [50] | Pratt R G. 1990. Frequency-domain elastic wave modeling by finite differences: A tool for crosshole seismic imaging[J]. Geophysics, 55(5): 626-632. |
| [51] | Pratt R G, Worthington M H. 1990. Inverse theory applied to multi-source cross-hole tomography, Part 1: acoustic wave-equation method[J]. Geophysical Prospecting, 38(3): 287-310. |
| [52] | Pratt R G, Bauer K, Weber M. 2003. Crosshole waveform tomography velocity and attenuation images of arctic gas hydrates[C]. // 73th Annual International Meeting, Society of Exploration Geophysicists, Expanded Abstracts, 2255-2258. |
| [53] | Priest J A, Best A I, Clayton C R. 2006. Attenuation of seismic waves in methane gas hydrate-bearing sand[J]. Geophysical Journal International, 164(1): 149-159. |
| [54] | Pyun S, Shin C, Lee H, et al. 2008. 3D elastic full waveform inversion in the Laplace domain[C]. // 78th Annual International Meeting, Society of Exploration Geophysicists, Expanded Abstracts, 1976-1980. |
| [55] | Queiβer M, Singh S C. 2013. Full waveform inversion in the time lapse mode applied to CO2 storage at Sleipner[J]. Geophysical Prospecting, 61(3): 537-555. |
| [56] | Rossi G, Gei D, Böhm G, et al. 2007. Attenuation tomography: An application to gas-hydrate and free-gas detection[J]. Geophysical Prospecting, 55(5): 655-669. |
| [57] | Sain K, Minshull T A, Singh S C, et al. 2000. Evidence for a thick free gas layer beneath the bottom simulating reflector in the Makran accretionary prism[J]. Marine Geology, 164(1-2): 3-12. |
| [58] | Shin C, Cha Y H. 2008. Waveform inversion in the Laplace domain[J]. Geophysical Journal International, 173(3): 922-931. |
| [59] | Shin C, Cha Y H. 2009. Waveform inversion in the Laplace-Fourier domain[J]. Geophysical Journal International, 177(3): 1067-1079. |
| [60] | Singh S C, Dietrich M, Chapel F. 1991. A complete waveform inversion and its application to ECORS data[J]. Continental Lithosphere: Deep Seismic Reflections, 22: 391-400. |
| [61] | Singh S C, Minshull T A, Spence G D. 1993. Velocity structure of a gas hydrate reflector[J]. Science, 260(5105): 204-207. |
| [62] | Singh S C, Minshull T A. 1994. Velocity structure of a gas hydrate reflector at Ocean Drilling Program site 889 from a global seismic waveform inversion[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 99(B12): 24221-24233. |
| [63] | Song H B, Mstsubayashi O, Yang S X, et al. 2002. Physical property models of gas hydrate-bearing sediments and AVA character of bottom simulating reflector[J]. Chinese Journal of Geophysics (in Chinese), 45(4): 546-556, doi: 10.3321/j.issn:0001-5733.2002.04.012. |
| [64] | Song H B, Mstsubayashi O, Kuramoto S. 2003. Full waveform inversion of gas hydrate related bottom simulating reflectors[J]. Chinese Journal of Geophysics (in Chinese), 46(1): 42-46. |
| [65] | Sun Y B, Wu S G, Dong D D, et al. 2012. Gas hydrates associated with gas chimneys in fine-grained sediments of the northern South China Sea[J]. Marine Geology, 311: 32-40. |
| [66] | Tarantola A. 1984a. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 49(8): 1259-1266. |
| [67] | Tarantola A. 1984b. Linearized inversion of seismic reflection data[J]. Geophysical Prospecting, 32(6): 998-1015. |
| [68] | Tarantola A. 1986. A strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics, 51(10): 1893-1903. |
| [69] | Tarantola A. 1988. Theoretical background for the inversion of seismic waveforms including elasticity and attenuation[J]. Pure and Applied Geophysics, 128(1-2): 365-399. |
| [70] | Thomsen L. 1986. Weak elastic anisotropy[J]. Geophysics, 51(10): 1954-1966. |
| [71] | Tinivella U, Accaino F. 2000. Compressional velocity structure and Poisson's ratio in marine sediments with gas hydrate and free gas by inversion of reflected and refracted seismic data (South Shetland Islands, Antarctica)[J]. Marine Geology, 164(1): 13-27. |
| [72] | Virieux J, Operto S. 2009. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 74(6): WCC1-WCC26. |
| [73] | Watanabe T, Shimizu S, Asakawa E, et al. 2004. Differential waveform tomography for time-lapse crosswell seismic data with application to gas hydrate production monitoring[C]. // 74th Annual International Meeting, Society of Exploration Geophysicists, Expanded Abstracts, 2323-2326. |
| [74] | Westbrook G K, Chand S, Rossi G, et al. 2008. Estimation of gas hydrate concentration from multi-component seismic data at sites on the continental margins of NW Svalbard and the Storegga region of Norway[J]. Marine and Petroleum Geology, 25(8): 744-758. |
| [75] | Xia G Y, Sen M K, Stoffa P L. 1998. 1-D elastic waveform inversion: A divide-and-conquer approach[J]. Geophysics, 63(5): 1670-1684. |
| [76] | Xia G Y, Sen M K, Stoffa P L. 2000. Mapping of elastic properties of gas hydrates in the Carolina trough by waveform inversion[J]. Geophysics, 65(3): 735-744. |
| [77] | Xu K, Wang M Y. 2004. Frequency-domain finite-element inversion of elastic-wave velocity using the geological regular-blocky-model method[J]. Chinese Journal of Geophysics (in Chinese), 47(4): 708-717, doi: 10.3321/j.issn:0001-5733.2004.04.024. |
| [78] | Yang J Z, Liu Y Z, Dong L G. 2014. A multi-parameter full waveform inversion strategy for acoustic media with variable density[J]. Chinese Journal of Geophysics (in Chinese), 57(2): 628-643, doi: 10.6038/cjg20140226. |
| [79] | Yang R, Wu N Y, Bai J, et al. 2013. Gas hydrate identification in non-BSR region, northern South China Sea[J]. Progress in Geophysics (in Chinese), 28(2): 1033-1040, doi: 10.6038/pg20130257. |
| [80] | Yang W Y, Wang X W, Yong X S, et al. 2013. The review of seismic full waveform inversion method[J]. Progress in Geophysics (in Chinese), 28(2): 766-776, doi: 10.6038/pg20130225. |
| [81] | Yuan T, Hyndman R D, Spence G D, et al. 1996. Seismic velocity increase and deep-sea gas hydrate concentration above a bottom-simulating reflector on the northern Cascadia continental slope[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 101(B6): 13655-13671. |
| [82] | Yuan T, Spence G D, Hyndman R D, et al. 1999. Seismic velocity studies of a gas hydrate bottom-simulating reflector on the northern Cascadia continental margin: Amplitude modeling and full waveform inversion[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 104(B1): 1179-1191. |
| [83] | Zhang G X, Xu H N, Liu X W, et al. 2014. The acoustic velocity characteristics of sediment with gas hydrate revealed by integrated exploration of 3D seismic and OBS data in Shenhu area[J]. Chinese Journal of Geophysics (in Chinese), 57(4): 1169-1176, doi: 10.6038/cjg20140414. |
| [84] | Zhou B, Greenhalgh S A. 2003. Crosshole seismic inversion with normalized full-waveform amplitude data[J]. Geophysics, 68(4): 1320-1330. |
| [85] | 卞爱飞. 2011. 反射地震学全波形反演理论与应用研究[博士论文]. 武汉: 中国地质大学(武汉). |
| [86] | 卞爱飞, 於文辉, 周华伟. 2010. 频率域全波形反演方法研究进展[J]. 地球物理学进展, 25(3): 982-993, doi: 10.3969/j.issn.1004-2903.2010.03.037. |
| [87] | 高凤霞, 刘财, 冯晅等. 2013. 几种优化方法在频率域全波形反演中的应用效果及对比分析研究[J]. 地球物理学进展, 28(4): 2060-2068, doi: 10.6038/pg20130450. |
| [88] | 霍元媛, 张明. 2010. 基于遗传算法的天然气水合物似海底反射层速度结构全波形反演[J]. 石油地球物理勘探, 45(1): 55-59. |
| [89] | 宋海斌, Mstsubayashi O, 杨胜雄,等. 2002. 含天然气水合物沉积物的岩石物性模型与似海底反射层的AVA特征[J]. 地球物理学报, 45(4): 546-556, doi: 10.3321/j.issn:0001-5733.2002.04.012. |
| [90] | 宋海斌, Mstsubayashi O, Kuramoto S. 2003. 天然气水合物似海底反射层的全波形反演[J]. 地球物理学报, 46(1): 42-46. |
| [91] | 许琨, 王妙月. 2001. 声波方程频率域有限元参数反演[J]. 地球物理学报, 44(6): 852-864, doi: 10.3321/j.issn:0001-5733.2001.06.015. |
| [92] | 许琨, 王妙月. 2004. 利用地质规则块体建模方法的频率域有限元弹性波速度反演[J]. 地球物理学报, 47(4): 708-717, doi: 10.3321/j.issn:0001-5733.2004.04.024. |
| [93] | 杨积忠, 刘玉柱, 董良国. 2014. 变密度声波方程多参数全波形反演策略[J]. 地球物理学报, 57(2): 628-643, doi: 10.6038/cjg20140226. |
| [94] | 杨睿, 吴能友, 白杰等. 2013. 南海北部无明显BSR地区天然气水合物识别研究[J]. 地球物理学进展, 28(2): 1033-1040, doi: 10.6038/pg20130257. |
| [95] | 杨午阳,王西文,雍学善,等.2013.地震全波形反演方法研究综述[J].地球物理学进展, 28(2): 766-776, doi: 10.6038/pg20130225. |
| [96] | 张光学, 徐华宁, 刘学伟,等. 2014. 三维地震与OBS联合勘探揭示的神狐海域含水合物地层声波速度特征[J]. 地球物理学报, 57(4): 1169-1176, doi: 10.6038/cjg20140414. |
 2015, Vol. 30
2015, Vol. 30

