叠前深度偏移是进行叠前成像和偏移速度建模的重要方法技术.目前,偏移速度建模是叠前深度偏移中迫切需要解决的问题之一,这主要是因为波动方程叠前深度偏移对成像速度场非常敏感.我们可以利用偏移成像结果对偏移速度模型的敏感性,建立适当的速度误差判别准则及速度更新函数,来修改初始偏移速度模型,直到得到最佳偏移速度模型.但是,如何选择一种合理有效的用于偏移速度分析的共成像点道集,引起了广大地球物理学家的关注,基于ADCIG的速度分析方法也已经成为偏移速度分析领域研究的一个热点,如Sava等(Sava and Formel,2000a,b,2003,2005; Sava and Biondi,2004a,b); Biondi和Symes(2004); Biondi和Tisserant(2004).朱莉(2009)利用RMO在ADCIG进行偏移速度建模,取得了较好结果.程玖兵等(程玖兵等,2002,2003,2005; 程玖兵和马在田,2011)通过对地震波局部方向特征的分析,讨论了适用于各向同性与各向异性介质的方位保真局部角度域叠前偏移成像原理及其应用方法.刘文卿等(2010)以共反射角偏移方法为基础,研究共反射角道集构建、旅行时计算及几何扩散因子获取及偏移拉伸对共反射角道集的影响.张敏等(2011)应用双平方根保幅波动方程叠前深度偏移输出ADCIG及成像结果,为后续偏移速度分析和AVO分析提供可靠的数据.耿瑜等(2012)在采用局部指数标架小波束进行角度域方向照明分析的基础上,研究采集系统对复杂盐丘下部层状结构成像质量的影响.ADCIG凭借其自身优越性被广泛推崇,利用ADCIG不仅可以进行偏移速度分析,还可以进行AVO/AVA等地震属性分析,得到与速度、岩性和流体有关的信息;同时,还可以对共成像点道集进行适当的去噪和剩余静校正处理,然后再叠加成像,这样会进一步提高构造图像的成像效果.
1 双平方根算子基本原理对于地震波场的延拓过程,可以在炮域使用单平方根算子来实现,也可以在中点-偏移距域根据“测线下延”原理,使用双平方根算子对记录波场进行反向外推.
如果将炮点和检波点同时向下外推同样的深度,把炮、检点坐标变换到中心点-偏移距域坐标,得到(刘定进和印兴耀,2007)

将(1)式变换到频率-波数域,得到用于叠前深度偏移的双平方根波场延拓算子为
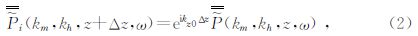

(2)式和(3)式即构成了中点-偏移距域的裂步傅立叶双平方根波场延拓算子.其中,km,kh为中心点坐标分量与偏移距分量的波数,${\overline{\overline {\tilde P}} _i}$i(km,kh,z+Δz;ω)为背景慢度引起的波场,Pu(km,kh,z+detaz,w)为扰动慢度引起的散射波场.
2 成像条件角度域共成像道集的提取总是建立在偏移距域共成像点道集已知的前提下,无论是从炮域单平方根算子中提取ADCIG,还是从中点-偏移距域双平方根算子中提取ADCIG,在获取ADCIG之前,都必须首先构建局部的ODCIG.因此,在讨论ADCIG道集的提取之前,重点研究局部ODCIG道集的构建过程.论文关于ADCIG的道集的提取都是从双平方根算子出发的,采用中点-偏移距域的双平方算子,在波场延拓过程中可以很自然的得到ODCIG.
为了保留与反射角度有关的反射信息,需要对传统成像条件进行修改,采用零时间、非零偏移距局部成像条件,成像过程中保留与反射角度有关的局部偏移距信息.采用局部成像条件可以在成像点附近对波场进行部分成像,得到与反射角度有关的ODCIG,局部成像公式为
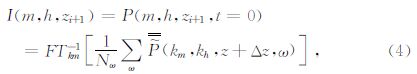
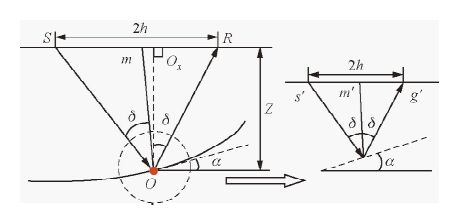
由于ADCIG对射线多路径问题的适应性,很多学者对它非常关注,因此形成了相应的抽取算法(Sava and Fomel,2003).图 1反映了常速介质下具有单层反射界面的射线传播情况,其中,炮点Source为入射射线、检波点Re ceiver为反射射线,它们和地面构成了一个三角关系,从该三角关系出发可以推出所有变量之间的简单关系式.图 1中,α表示地层倾角,δ表示局部入射角,v是地层速度,2h是地表偏移距,Z表示反射点的深度.
|
图 1 反射点局部反射示意图 Fig. 1 Schematic diagram of partial reflection in the reflection point |
Sava and Fomol(2003)给出了频率-波数域纵波ADCIG的转换公式为

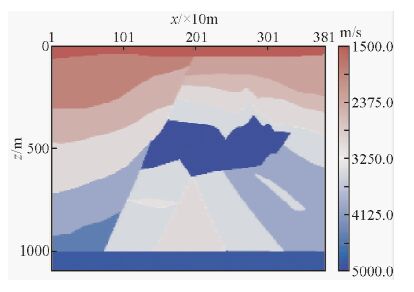
为了验证角度域共成像点道集对复杂模型的适应性,将其应用到SEG/EAGE岩丘模型.图 2为SEG/EAGE岩丘模型的纵波速度模型,模型横向宽为3800 m,垂向1100 m.纵波速度最小值和最大值分别为1500 m/s,5000 m/s;炮集记录采用标量波动方程方法计算得到,合成数据总共140炮,第一炮位于速度模型表层X为980 m处,炮间距20 m,每炮98道接收,最小偏移距0 m,最大偏移距970 m,道距10 m;采样间隔0.002 s,采样长度2.0 s.延拓步长4 m,延拓深度1100 m .
|
图 2 SEG/EAGE岩丘纵波速度模型 Fig. 2 SEG/EAGE rock mound P-wave velocity model |
图 3 为DSR全角度波动方程叠前深度偏移成像结果,图 4a和4b分别表示ANGLE-45和ANGLE-15度DSR波动方程叠前深度偏移成像结果(ANGLE-45表示最大入射角为45度,ANGLE-15表示最大入射角为15度);从图中可以看出,采用双平方根(DSR)波动方程叠前深度偏移,基本上已经恢复了岩丘模型的层位构造.对于不同入射角范围的偏移成像结果,可以突出岩丘模型局部成像效果,如ADCIG-15的偏移成像结果,与ADCIG-45和全角度成像结果相比,前者对岩丘底部成像更好,边界成像能量更强,底部层位也慢慢凸显出来.

|
图 3 DSR叠前深度偏移剖面 Fig. 3 DSR pre-stack depth migration profile |

|
图 4 (a)DSR叠前深度偏移剖面(ANGLE-45度);(b)DSR叠前深度偏移剖面(ANGLE-15度) Fig. 4 (a)DSR pre-stack depth migration profile(ANGLE-45 degrees); (b)DSR pre-stack depth migration profile(ANGLE-15 degrees) |
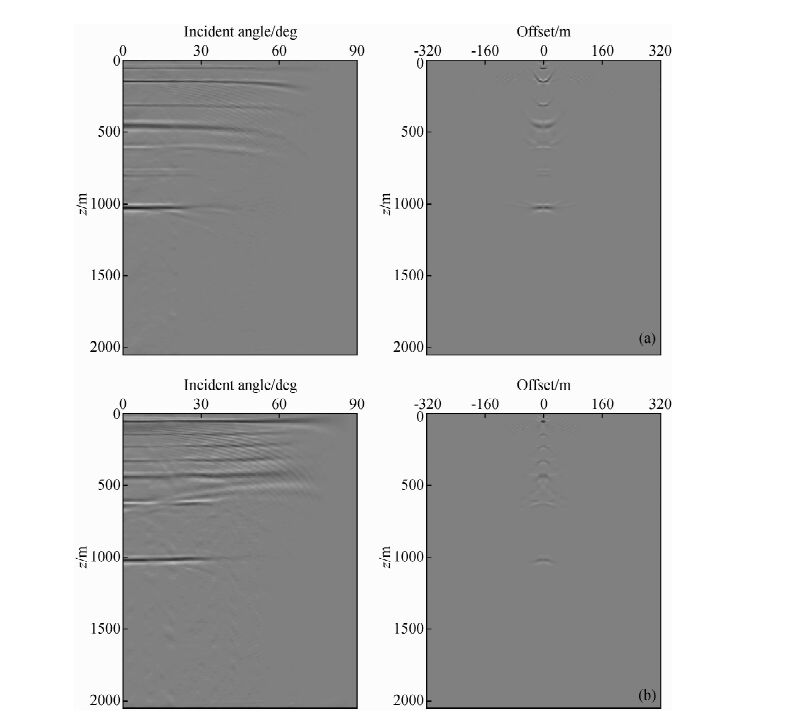
图 5a和图 5b分别为SEG/EAGE岩丘模型CMP200和CMP400处的ADCIG和ODCIG道集,从图中可以看出,对任意一个CMP道集,ADCIG道集由浅到深同相轴逐渐缩短,说明浅层对应的反射角信息更广,深层反射角逐渐减小,但ADCIG的同相轴仍旧是平坦的,这说明了ODCIG道集在零偏移距处聚焦较强.
|
图 5 (a)模型CMP-200处ODCIG和ADCIG道集;(b)模型CMP-400处ODCIG和ADCIG道集 Fig. 5 (a)ODCIG and ADCIG gathers at CMP-200;(b)ODCIG and ADCIG gathers at CMP-400 |
在中点-偏移距域采用双平方根算子偏移具有边界处理简单、无需求取震源子波、倾角假频少、无需考虑偏移孔径以及计算效率高等特点.通过对ODCIG和ADCIG道集进行分析研究,表明ODCIG是一种能量聚焦型的道集,当偏移速度模型正确时,ODCIG表现为聚焦于零偏移距处的能量,与ODCIG不同,波动方程ADCIG是没有假象的道集,当速度正确时,ADCIG同相轴是拉平的道集.在叠加成像时,将波场变换到ADCIG道集,然后通过对不同入射角范围的波场进行叠加成像.叠加效果表明,采用不同入射角范围的波场进行成像时,可以突出地下不同的结构信息,同时,ADCIG道集反映了波场与入射角的关系,这为AVO/AVA等地震资料属性分析及后续地震资料处理提供了可靠的依据.
致 谢 感谢审稿专家提出的宝贵修改意见和编辑部的大力支持!
| [1] | Biondi B, Tisserant T. 2004. 3D angle-domain common-image gathers for migration velocity analysis[J]. Geophysical Prospecting, 52(6): 575-591. |
| [2] | Biondi B, Symes W W. 2004. Angle-domain common-image gathers for migration velocity analysis by wavefield-continuation imaging[J]. Geophysics, 69(5): 1283-1298. |
| [3] | Chen L, Wu R S, Wang W J. 2004. Common angle image gathers obtained from Gabor-Daubechies beamlet prestack depth migration[J]. Chinese Journal of Geophysics (in Chinese), 47(5): 876-885, doi: 10.3321/j.issn:0001-5733.2004.05.020. |
| [4] | Cheng J B, Ma Z T. 2011. Azimuth-preserved local angle domain imaging for objects[J]. Oil Geophysical Prospecting (in Chinese), 46(3): 374-385. |
| [5] | Cheng J B, Wang H Z, Ma Z T. 2002. Pre-stack Depth migration with finite-difference method in frequency-space domain[J]. Chinese Journal of Geophysics (in Chinese), 44(3): 389-395, doi: 10.3321/j.issn:0001-5733.2001.03.011. |
| [6] | Cheng J B, Wang H Z, Ma Z T. 2003. Double square root equation 3D prestack depth migration[J]. Chinese Journal of Geophysics (in Chinese), 46(5): 676-683, doi: 10.3321/j.issn:0001-5733.2003.05.015. |
| [7] | Cheng J B, Wang H Z, Ma Z T. 2005. Double square root equation migration methods of narrow azimuth seismic data[J]. Chinese Journal of Geophysics (in Chinese), 48(2): 399-405, doi: 10.3321/j.issn:0001-5733.2005.02.024. |
| [8] | Cui X F, Zhang G Q, He Z Q. 2004. Velocity analysis on wavefiled continued gathers from double squared root operator[J]. Geophysical Prospecting for Petroleum (in Chinese), 43(1): 16-19, doi: 10.3969/j.issn.1000-1441.2004.01.004. |
| [9] | Duan P F, Cheng J B, Chen A P, et al. 2013. Local angle-domain Gaussian beam prestack depth migration in a TI medium[J]. Chinese Journal of Geophysics (in Chinese), 56(12): 4206-4214, doi: 10.6038/cjg20131223. |
| [10] | Duan P F, Cheng J B, Chen S P, et al. 2013. Local angle-domain ray tracing and prestack depth migration in TI medium[J]. Chinese Journal of Geophysics (in Chinese), 56(1): 269-279, doi: 10.6038/cjg20130128. |
| [11] | Geng J H, Ma Z T, Wang H Z, et al. 1998. Prestack depth migration by wave equation finite difference[J]. Chinese Journal of Geophysics (in Chinese), 41(3): 392-399. |
| [12] | Geng Y, Mao J, Wu R S, et al. 2012. Local angle domain target oriented illumination analysis and imaging using beamlets[J]. Chinese Journal of Geophysics (in Chinese), 55(3): 981-990, doi: 10.6038/j.issn.0001-5733.2012.03.028. |
| [13] | Liu D J, Yin X Y. 2007. Amplitude-preserved seismic migration based on double square root[J]. Oil Geophysical Prospecting (in Chinese), 42(1): 11-16. |
| [14] | Liu L N, Liu H, Li Y M. 2004. Wave-equation 3-D prestack depth migration for the SEG/EAGE salt and over thrust model[J]. Chinese Journal of Geophysics (in Chinese), 47(2): 312-320. |
| [15] | Liu L N, Zhang H, Zhang J F. 2013. Angle gathers for one-way wave equation shot-record migration methods[J]. Chinese Journal of Geophysics (in Chinese), 56(9): 3124-3133, doi: 10.6038/cjg20130925. |
| [16] | Liu W Q, Wang X W, Wang Y C, et al. 2010, Angle domain pre-stack migration imaging studies and application[J]. Oil Geophysical Prospecting (in Chinese), 45(S1): 62-65. |
| [17] | Ma Z T. 1983. A splitting-up method for solution of higher-order migration equation by finite-difference scheme[J]. Chinese Journal of Geophysics (in Chinese), 26(4): 377-388. |
| [18] | Sava P, Fomel S. 2000. Angle-gathers by Fourier transform[J]. Geophysics, 103: 391-402. |
| [19] | Sava P, Fomel S. 2003. Angle-domain common-image gathers by wavefield continuation methods[J]. Geophysics, 68(3): 1065-1074. |
| [20] | Sava P, Biondi B. 2004a. Wave-equation migration velocity analysis. I: Theory[J].Geophysical Prospecting, 52(6): 593-606. |
| [21] | Sava P, Biondi B. 2004b. Wave-equation migration velocity analysis. II: Subsalt imaging examples[J].Geophysical Prospecting, 52(6): 607-623. |
| [22] | Sava P, Fomel S. 2005. Coordinate-independent angle-gathers for wave equation migration[J]. SEG Technical Program Expanded Abstracts, 2052-2055, doi: 10.1190/1.2148114. |
| [23] | Wang H Z, Feng B, Liu S Y, et al. 2015. Characteristic wavefield decomposition, imaging and inversion with prestack seismic data[J]. Chinese Journal of Geophysics (in Chinese), 58(6): 2024-2034, doi: 10.6038/cjg20150617. |
| [24] | Wang W Z, Tsingas C. 2001. Converted-wave pre-stack imaging and velocity analysis by pseudo-offset migration[J]. First Break, 20(11) |
| [25] | Xu S, Lambaré G. 2006. True amplitude Kirchhoff prestack depth migration in complex media [J]. Chinese Journal of Geophysics (in Chinese), 49(5): 1431-1444. |
| [26] | Yang C C, Liu X C, Li Y M, et al. 1996. A methodology for seismic prestack depth migration[J]. Chinese Journal of Geophysics (in Chinese), 39(3): 409-415. |
| [27] | Zhang G Q. 1986. Steep Dip finite-difference migration using the system of lower-order partial differential equations[J]. Chinese Journal of Geophysics (in Chinese), 29(3): 273-282. |
| [28] | Zhang M, Li Z C, Ye Y M, et al. 2011. Amplitude-preserved imaging based on double square root wave-equation in angle domain[J]. Journal of China university of Petroleum (in Chinese), 35(2), 45-50, doi: 10.3969/j.issn.1673-5005.2011.02.008. |
| [29] | Zhang Y. 2006. The theory of true amplitude one way wave equation migration[J]. Chinese Journal of Geophysics (in Chinese), 49(5): 1410-1430. |
| [30] | Zhang Y, Xu S, Zhang G Q, et al. 2007. True amplitude turning-wave one-way wave equation migration[J]. Geophysical Prospecting for Petroleum (in Chinese). 46(6): 582-587, 642, doi: 10.3969/j.issn.1000-1441.2007.06.010. |
| [31] | Zhu L. 2009. Migration velocity analysis based on common image point gathers in angle domain (in Chinese) [D]. Dongying: China University of Petroleum (East China). |
| [32] | 陈凌, 吴如山, 王伟君. 2004. 基于Gabor-Daubechies小波束叠前深度偏移的角度域共成像道集[J]. 地球物理学报, 47(5): 876-885, doi: 10.3321/j.issn:0001-5733.2004.05.020. |
| [33] | 程玖兵, 王华忠, 马在田. 2002. 频率-空间域有限差分法叠前深度偏移[J]. 地球物理学报, 44(3): 389-395, doi: 10.3321/j.issn:0001-5733.2001.03.011. |
| [34] | 程玖兵, 王华忠, 马在田. 2003. 双平方根方程三维叠前深度偏移[J]. 地球物理学报, 46(5): 676-683, doi: 10.3321/j.issn:0001-5733.2003.05.015. |
| [35] | 程玖兵, 王华忠, 马在田. 2005. 窄方位地震数据双平方根方程偏移方法探讨[J]. 地球物理学报, 48(2): 399-405, doi: 10.3321/j.issn:0001-5733.2005.02.024. |
| [36] | 程玖兵, 马在田. 2011. 针对目标的方位保真局部角度域成像方法[J]. 石油地球物理勘探, 46(3): 374-385. |
| [37] | 崔兴福, 张关泉, 何忠泉. 2004. 双平方根算子波场延拓道集速度分析[J]. 石油物探, 43(1): 16-19, doi: 10.3969/j.issn.1000-1441.2004.01.004. |
| [38] | 段鹏飞, 程玖兵, 陈三平,等. 2013. 介质局部角度域射线追踪与叠前深度偏移成像[J]. 地球物理学报, 56(1): 269-279, doi: 10.6038/cjg20130128. |
| [39] | 段鹏飞, 程玖兵, 陈爱萍,等. 2013. TI介质局部角度域高斯束叠前深度偏移成像[J]. 地球物理学报, 56(12): 4206-4214, doi: 10.6038/cjg20131223. |
| [40] | 耿建华, 马在田, 王华忠,等. 1998. 波动方程有限差分法叠前深度偏移[J]. 地球物理学报, 41(3): 392-399. |
| [41] | 耿瑜, 毛剑, 吴如山,等. 2012. 基于目标区的局部角度域方向照明分析及其在偏移成像中的应用[J]. 地球物理学报, 55(3): 981-990, doi: 10.6038/j.issn.0001-5733.2012.03.028. |
| [42] | 刘定进, 印兴耀. 2007. 基于双平方根方程的保幅地震偏移[J]. 石油地球物理勘探, 42(1): 11-16. |
| [43] | 刘礼农, 刘洪, 李幼铭. 2004. SEG/EAGE盐丘和推覆体模型的波动方程三维叠前深度偏移成像[J]. 地球物理学报, 47(2): 312-320. |
| [44] | 刘礼农, 张辉, 张剑锋. 2013. 波动方程叠前深度偏移直接产生角道集[J]. 地球物理学报, 56(9): 3124-3133, doi: 10.6038/cjg20130925. |
| [45] | 刘文卿, 王西文, 王宇超,等. 2010. 角度域叠前偏移成像研究及应用[J]. 石油地球物理勘探, 45(增刊1): 62-65. |
| [46] | 马在田. 1983. 高阶方程偏移的分裂算法[J]. 地球物理学报, 26(4): 377-388. |
| [47] | 王华忠, 冯波, 刘少勇,等. 2015. 叠前地震数据特征波场分解、偏移成像与层析反演[J]. 地球物理学报, 58(6): 2024-2034, doi: 10.6038/cjg20150617. |
| [48] | 徐升, Lambaré G. 2006. 复杂介质下保真振幅Kirchhoff深度偏移[J]. 地球物理学报, 49(5): 1431-1444. |
| [49] | 杨长春, 刘兴材, 李幼铭,等. 1996. 地震叠前深度偏移方法流程及应用[J]. 地球物理学报, 39(3): 409-415. |
| [50] | 张关泉. 1986. 利用低阶偏微分方程组的大倾角差分偏移[J]. 地球物理学报, 29(3): 273-282. |
| [51] | 张敏, 李振春, 叶月明,等. 2011. 基于双平方根算子的保幅角度域成像[J]. 中国石油大学学报, 35(2), 45-50, doi: 10.3969/j.issn.1673-5005.2011.02.008. |
| [52] | 张宇. 2006. 振幅保真的单程波方程偏移理论[J]. 地球物理学报, 49(5): 1410-1430. |
| [53] | 张宇, 徐升, 张关泉,等. 2007. 真振幅全倾角单程波方程偏移方法[J]. 石油物探, 46(6): 582-587, 642, doi: 10.3969/j.issn.1000-1441.2007.06.010. |
| [54] | 朱莉. 2009. 基于角度域共成像点道集的偏移速度分析[D]. 东营: 中国石油大学. |
 2015, Vol. 30
2015, Vol. 30

