2. 武汉大学测绘学院 武汉市珞喻路129号, 武汉 430079
2. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
当前,锚杆锚固技术作为各类地下工程(洞室、隧道等)及边坡护理的主要手段,已在水利水电、高速公路、人工隧道和人工高边坡等工程建设中得到广泛应用,其锚固质量的检测和运行状况的监测问题已被提到重要议事日程.早期的锚杆锚固质量检测方法主要是现场抗拔和中心取样法,这些方法虽然比较直观,但都是具有破坏性的有损检测,耗时且费用高,不能对锚杆锚固质量给予充分肯定(Zou,2004),已逐步被无损检测方法所取代.
弹性波法是锚杆锚固质量无损检测的主要方法,基本原理如图 1所示.通常的检测方法是在锚杆顶端布置激发和接收换能器,发射换能器所发射的弹性波沿锚杆向下传播,当遇到波阻抗发生变化时会产生反射波.通过对所接收到的反射波波形进行时域和频域分析(王靖涛,2003;王军民等,2004;尹健民等,2011),可以获得锚杆的长度、砂浆缺陷位置、砂浆饱满度等参数,并可据此对锚杆锚固质量进行评价.目前,弹性波法虽然得到广泛应用,但其理论研究工作却十分欠缺.其主要原因,是锚杆锚固体系条件下的波场计算问题有相当大的技术难度.众所周知,锚杆锚固体系的波传播问题最终归结为半无限空间条件下有限长柱状多层介质的波动方程的求解问题.在这样的边界条件下,要获得其解析解是不可能的.当考虑到围岩介质的非均匀性以及砂浆缺陷等因素的影响时,问题将会变得非常复杂.有鉴于此,到目前为止,国内外仅钟宏伟于2005年以柱状多层固体介质为对象研究了弹性波的传播规律以及在柱状多层固体介质中导波的频散特性(钟宏伟,2005);李张明于2007年研究了锚杆围岩系统瞬态激励响应的数学模型及其数值解法(李张明,2007)外,其余则很少有人涉足.

|
图 1 弹性波法原理图 Fig. 1 The theory diagram of elastic wave method |
毫无疑问,基于三维条件下锚杆锚固质量体系波传播问题的理论工作对锚杆检测仪器的设计、长度及砂浆饱满度的求取等问题非常重要.但由于问题的复杂性,目前的锚杆锚固体系波传播问题的理论研究工作基本都是将锚杆体系作为一维杆状体来建立数学模型,通过求解一维波动方程的方法来描述波在锚杆锚固体系中的传播问题的(雷林源和杨长特,1992;王成等,2000;Wang and Wang,2001;Ivanovic et al.,2002;朱国维等,2002;Beard and Lowe,2003;彭斌等,2003;杨湖和王成,2003;许明等,2003;李维树,2003;许明等,2003;刘盛东和张平松,2004).最典型的例子是王成等人将锚杆在岩体中的一端的边界条件按非线性情况考虑,用摄动法来求解线性波动方程,以获得到锚杆体系的动力学方程的近似解;许明等人通过将非齐次边界条件齐次化的方法,推导了一维非齐次波动方程在有界域情况下的解析解,并运用有限元数值方法进行了计算.这些方法虽然大大简化了数学计算,但是将锚杆锚固质量检测问题单一的视为一维问题处理,对指导实际锚杆检测仪器系统的设计以及有效波的利用等方面的工作还存在很多问题,特别是对砂浆饱满度的求取意义不大.此外,在如何激发有利于锚杆锚固质量检测的某些模式波以及有效波的识别和提取等问题上,依然没有找到最优选择.近年来一些研究学者针对此类问题展开了一系列的研究工作,2006年张昌锁等人对实验室的锚固锚杆模型进行数值模拟,找到了能看清模型底端反射的最佳激发波(张昌锁等,2006);2008年李义等人利用应力波反射法,通过分段截取发现了锚杆底端反射的显现与否与锚杆波长、自由段长度之间的定量关系,并提出固结波速的概念等等(李义等,2008),这些都为今后的实际工作奠定了重要的理论基础.
本文针对锚杆锚固质量弹性波检测理论研究工作欠缺的问题,开展了锚杆锚固体系条件下的弹性波传播的正演问题研究.在数值模拟方面,由于目前都是使用ANSYS/LS-DYNA和FLAC3D有限元计算软件对声波或弹性波方程进行数值模拟(左风春,2010;张东方,2010;言志信等,2011;赵宇亮,2012).为摆脱这些软件技术的束缚,本文编写了二维弹性波交错网格有限差分程序,并在围岩、砂浆及缺陷等各种因素变化的条件下进行了相应的数值模拟计算.
1 基本计算方法二维各向同性介质中的弹性波一阶速度应力方程为
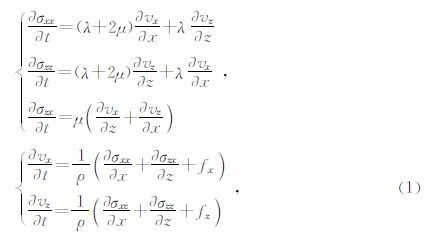
二维各向同性介质弹性波方程的交错网格有限差分法(Graves,1996)格式为
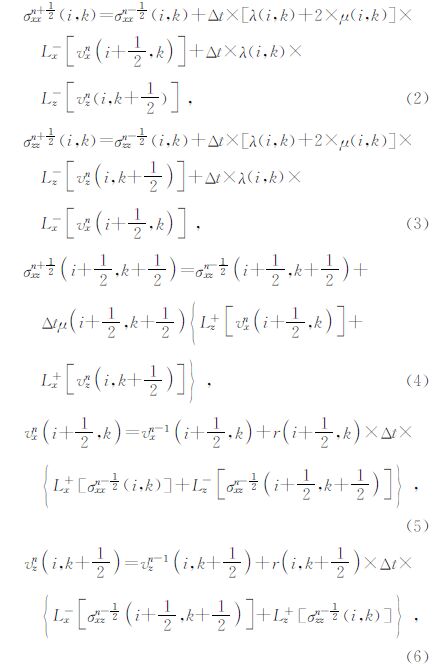

频散的稳定条件为
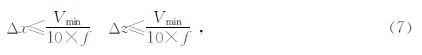
差分格式的稳定条件为


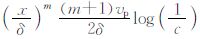 ,δ为吸收层宽度,一般取δ>λmax/2,x为吸收层内的点到吸收边界的距离,c为垂直入射时的反射系数,一般取c=10-3~10-5,m=2~5.
,δ为吸收层宽度,一般取δ>λmax/2,x为吸收层内的点到吸收边界的距离,c为垂直入射时的反射系数,一般取c=10-3~10-5,m=2~5.
采用C++编程实现算法,时间上2阶、空间上10阶差分,算法流程大致为:在时间循环计算中,先加载震源到vz上,接下来按公式(9)(10)(11)计算空间的应力循环,应力循环计算完后再按公式(12)(13)计算空间的速度循环,在每个时间循环计算完后将vx,vz保存到文件.
2 模型计算和分析 2.1 物理模型实验物理模型实验目的是为了检验数值模型计算的正确性.根据实际条件情况,从采石厂定制了一个灰岩模型,如图 2所示.该物理模型长度为0.455 m,直径为0.445 m,密度为2.686 g/cm3,纵波速度为6382 m/s,横波速度为3654 m/s.在模型中间钻孔,孔直径为0.0392 m.置入钻孔中的钢筋长度为0.479 m,直径为0.025 m,密度为7.852 g/cm3,纵波速度为5127 m/s,横波速度为3329 m/s.使用普通散装水泥,中粗砂,采用3:1的比例制作水泥砂浆.将岩柱直立,底部封闭,钢筋放置在孔的中间,灌入水泥砂浆,等水泥砂浆完全固结,然后进行测量.

|
图 2 锚杆锚固物理模型 Fig. 2 Physical model of rock bolts |
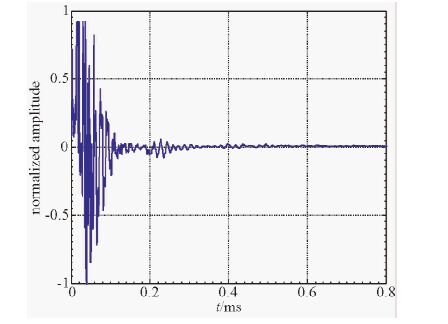
测量前先将钢筋的端头打磨平整,用黄油做耦合剂.使用主频为50 kHz的压电直探头,S1102E数字示波器、CTS-8077PR超声发射机和TST3206动态测试分析仪,在钢筋的端头采用单通道自激自收的采集方式,发射机脉冲电压为400 V,脉冲宽度为600 ns,采样频率为2000 K,采样点数为2048.为了减少误差,每次采集10道数据,将10道数据相加平均,作为一次采集的波形,做去均值和归一化处理.图 3为采集的波形图,可以看到,0.2 ms附近出现第一次反射波,由于衰减很大,第二次反射波不是特别明显.
|
图 3 物理模型实验采集的波形图 Fig. 3 Acquired waveform of physical model experiment |
本文采用与物理模型相近的数值模型,模型尺寸为1.2×0.6 m,孔的直径为0.04 m,钢筋的直径为0.025 m,钢筋的长度为0.5 m,在钢筋的中间位置进行激发和接收.介质的弹性参数如表 1所示.震源使用与实际接近的衰减正弦波,主频为50 kHz.水平和垂直方向的空间步长为0.0025 m,时间采样间隔为0.0002 ms,总采样时间为0.8 ms.模型的网格数为480×240,模型的周围再加上吸收层,吸收层的网格数为50.由于锚杆中传播的波是一种导波,计算十分复杂,虽有前人针对此问题做了一些具体理论计算工作,但都未全面考虑锚杆的所有问题,而是将锚杆看作各种理想化的模型,从而简化计算(左风春,2010;言志信等,2011;张东方,2010;赵宇亮,2012).这种办法虽与实际应用有一定偏差,但目前尚未有更好的办法计算此类问题,而且该办法也具有一定的理论指导意义.本文基于此种原因,暂不考虑钢筋的露头.
|
|
表 1 介质的弹性参数 Table 1 The parameters of the elastic medium |
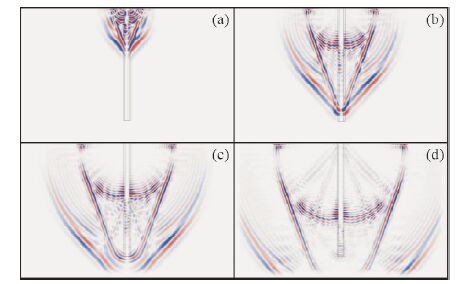
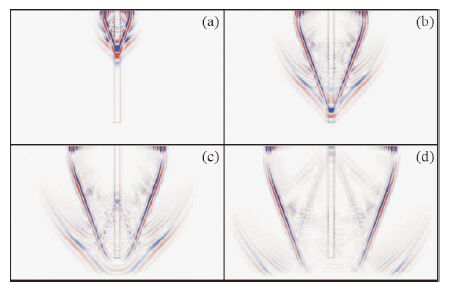
图 4和图 5分别为X分量和Z分量的波场快照,其中,图 4a-d分别是X分量在0.05 ms、0.1 ms、0.15 ms和0.2 ms时刻的波场快照,图 5a-d分别是Z分量在0.05 ms、0.1 ms、0.15 ms和0.2 ms时刻的波场快照.图 4b和图 5b中,可以看到两个V字形的波,其中夹角大的V字形波为沿钢筋传播的滑行波在围岩中产生的纵波,夹角小的V字形波为沿钢筋传播的滑行波在围岩中产生的横波.这两个V字形波的产生与水平层状介质地震勘探的折射波类似,不同的是无论围岩和砂浆的速度比钢筋的速度大还是小,都会产生V字形波.从三维视角看,这两个波为伞状的平面波,可以采用表面多道阵列接收,通过识别和追踪道集的同相轴来判断底部反射波.
图 4和图 5还可以看到在围岩中两个半圆弧形的波,其中大圆弧形的波为震源点产生的纵波,小圆弧形的波为震源点产生的横波;钢筋和砂浆里面存在大量的导波,随波场的持续越来越多;在夹角小的V字形里面还有很多更小的V字形波,这些波是由导波的振动产生.图 4c,d和图 5c、d中,可以看到在钢筋底部导波也会产生反射.对比图 4和图 5,可以看到,对于钢筋底部的反射波,Z分量的反映比X分量的要明显.
|
图 4 (a)X分量在0.05 ms时刻的波场快照; (b)X分量在0.1 ms时刻的波场快照; (c)X分量在0.15 ms时刻的波场快照; (d)X分量在0.2 ms时刻的波场快照 Fig. 4 (a)The snapshot of wave field of X component at 0.05 ms;(b)The snapshot of wave field of X component at 0.1 ms;(c)The snapshot of wave field of X component at 0.15 ms;(d)The snapshot of wave field of X component at 0.2 ms |
|
图 5 (a)Z分量在0.05 ms时刻的波场快照; (b)Z分量在0.1 ms时刻的波场快照; (c)Z分量在0.15 ms时刻的波场快照; (d)Z分量在0.2 ms时刻的波场快照 Fig. 5 (a)The snapshot of wave field of Z component at 0.05 ms ;(b)The snapshot of wave field of Z component at 0.1 ms;(c)The snapshot of wave field of Z component at 0.15 ms;(d)The snapshot of wave field of Z component at 0.2 ms; |
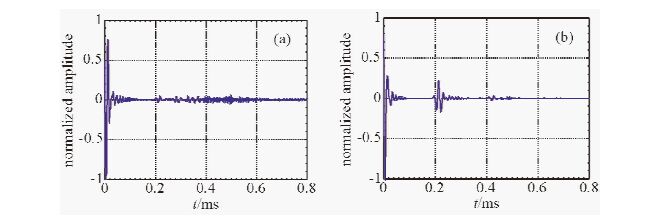
图 6a、b分别是接收点的X分量和Z分量的波形,波形归一化处理.可以看到,对于钢筋底部的反射首波(0.2 ms处),Z分量的反映比X分量的要明显,且Z分量的波形可以看到钢筋底部的第二次反射波(0.4 ms处).与物理模型实验波形对比,可以看到,数值模型的Z分量波形与物理模型结果基本一致,物理模型实验波形中震源首波持续时间长一些,反射波衰减比二维数值模型的要大.
|
图 6 (a)X分量的波形;(b)Z分量的波形 Fig. 6 (a)The waveform of X component;(b)The waveform of Z component |
从图 4、图 5和图 6,可以看到,钢筋底部的第一次反射波到第二次反射波之间的波形,存在很多导波,不利于现场检测.波形开始到钢筋底部的第一次反射波之间没有其他波的干扰,也就是说,Z分量中钢筋底部的第一次反射波对钢筋长度检测最有利,即现场检测中端发端收的采集方式优于端发侧收的采集方式.
3 各种因素对反射波形的影响 3.1 围岩对反射波形的影响假定模型尺寸、孔的直径、钢筋的直径、钢筋的长度、震源、水平和垂直方向的空间步长、时间采样间隔、总采样时间等与第3小节参数一样,不同的是考查6种不同类型围岩对反射波形的影响,弹性参数见表 2,假定围岩的密度变化不大.
|
|
表 2 介质的弹性参数 Table 2 The parameters of the elastic medium |
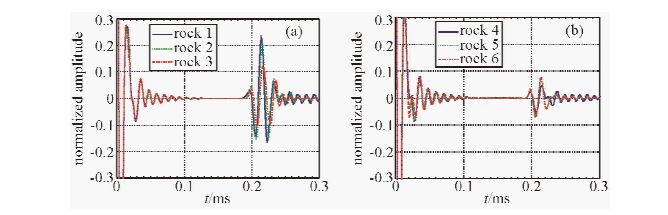
图 7a为围岩1、2、3的Z分量波形,图 7b为围岩4、5、6的Z分量波形,垂直方向显示范围为-0.3到0.3.可以看到,当围岩的纵波速度大于钢筋的纵波速度时,围岩的纵波速度越大,钢筋底部反射首波的振幅越大;当围岩的纵波速度小于钢筋的纵波速度时,围岩的纵波速度越小,钢筋底部反射首波的振幅越大.
|
图 7 (a)围岩1、2、3的Z分量波形;(b)围岩4、5、6的Z分量波形 Fig. 7 (a)The waveforms of Z component of surrounding rock 1,2,3; (b)The waveforms of Z component of surrounding rock 4,5,6 |
假定模型尺寸、孔的直径、钢筋的直径、钢筋的长度、震源、水平和垂直方向的空间步长、时间采样间隔、总采样时间等与第3小节参数一样,不同的是考查3种水泥砂浆对反射波形的影响,弹性参数见表 3,一般而言水泥砂浆的强度越大,其速度越大.假定水泥砂浆的密度变化不大.
|
|
表 3 介质的弹性参数 Table 3 The parameters of the elastic medium |
图 8为水泥砂浆1、2、3的Z分量波形.可以看到,当水泥砂浆的波速变低时,钢筋底部反射波的波至时间不变,但反射波的频率会随之有所降低.

|
图 8 水泥砂浆1、2、3的Z分量波形 Fig. 8 The waveforms of Z component of cement mortar 1,2,3 |
假定模型尺寸、孔的直径、钢筋的直径、钢筋的长度、震源与第3小节参数一样.缺陷放置在0.25 m处的砂浆中,缺陷1、2和3的垂直方向的长度分别为0.02 m、0.06 m和0.1 m.考虑到差分算法的稳定性,在缺陷里面填充低速介质,弹性参数见表 4.水平和垂直方向的空间步长为0.00025 m,时间采样间隔为0.00002 ms,总采样时间为0.8 ms.模型的网格数为4800×2400,吸收层的网格数为250.
|
|
表 4 介质的弹性参数 Table 4 The parameters of the elastic medium |
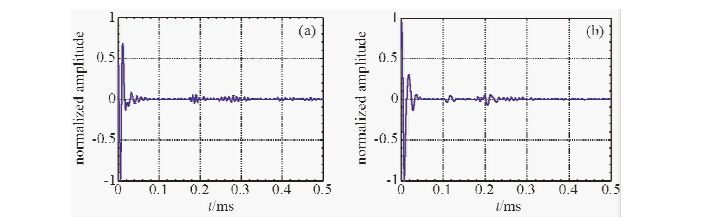
图 9a为X分量的波形,图 9b为Z分量的波形.可以看到,X分量的波形不能准确判定缺陷的位置;Z分量中可以明显看到缺陷的反射波(0.1 ms处)和钢筋底部的第一次反射波(0.2 ms处).
|
图 9 (a)X分量的波形;(b)Z分量的波形 Fig. 9 (a)The waveform of X component;(b)The waveform of Z component |
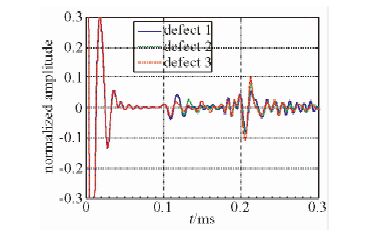
图 10为三种长度缺陷的Z分量波形.可以看到,缺陷长度越小,钢筋底部反射波的振幅越小;缺陷长度越大,钢筋底部反射波的振幅越大.原因是缺陷长度越小,水泥砂浆越密实,则沿钢筋传播的能量更多的传播到围岩中;相反,缺陷长度越大,越多的能量传播到钢筋底部产生反射.这也为砂浆饱满度检测的定量计算提供参考.
|
图 10 缺陷1、2、3的Z分量波形 Fig. 10 The waveforms of Z component of the defect 1,2,3 |
本文通过理论分析和模型实例的数值模拟,研究了围岩、水泥砂浆和砂浆缺陷对反射波形的影响,得到以下结论:
(1)对于钢筋底部和砂浆缺陷的反射波,垂直分量的反映比水平分量明显.也就是说,现场检测中端发端收的采集方式优于端发侧收的采集方式;
(2)可以采用表面多道阵列接收,通过识别和追踪道集的同相轴来判断底部反射波;
(3)当围岩的纵波速度大于钢筋的纵波速度时,围岩的纵波速度越大,钢筋底部反射首波的振幅越大;当围岩的纵波速度小于钢筋的纵波速度时,围岩的纵波速度越小,钢筋底部反射首波的振幅越大;
(4)当围岩的波速变低时,杆底反射波的波至时间不变,但反射波的频率会随之有所降低;
(5)砂浆缺陷越小,钢筋底部反射波的振幅越小;砂浆缺陷越大,钢筋底部反射波的振幅越大.
必须提及,本文建模时没有考虑锚杆外露端头的影响,这与实际情况有一定的差距,但若考虑这一因素,则其计算工作会变得十分复杂.这一缺憾将会在今后的工作中解决.此外,由于实验条件和经费有限,本文最后的两条结论需要进行进一步的野外实例验证,如若与实验吻合,则可以预料,锚杆砂浆饱满度的求取技术将会取得新的进展.
未来的一项重要研究工作是,研究反射波频率变化与砂浆饱满度的关系,根据两者之间的关系来推断砂浆的充填情况,这很可能是未来研究锚杆质量无损检测的新突破口.
致 谢 本文的研究成果旨在为现场实际锚杆质量弹性波检测提供参考和借鉴,不足之处还请各位专家批评指正.在此特别感谢国家自然科学基金及长江大学油气资源与勘探技术教育部重点实验室对本次研究工作的支持.
| [1] | Beard M D, Lowe M J S. 2003. Non-destructive testing of rock bolts using guided ultrasonic waves[J]. International Journal of Rock Mechanics and Mining Sciences, 40(4): 527-536. |
| [2] | Collino F, Tsogka C. 2001. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 66(1): 294-307. |
| [3] | Graves R W. 1996. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite difference[J]. Bulletin of the Seismological Society of America, 86(4): 1091-1106. |
| [4] | Ivanovic A, Neilson R D, Rodger A A. 2002. Influence of prestress on the dynamic response of ground anchorages[J]. Journal of Geotechnical and Geoenvironmental Engineering, 128(3): 237-249. |
| [5] | Lei L Y, Yang C T. 1992. The mathematical models and basic characters of transient response for dynamic test of pile[J]. Acta Geophysica Sinica (in Chinese), 35(4): 501-509. |
| [6] | Li W S, Gan G Q, Zhu R G, et al. 2003. Research on application of non-destructive detection technique to quality of grouting for engineering anchor bars[J]. Rock and Soil Mechanics (in Chinese), 24(S1): 189-194. |
| [7] | Li Y, Zhang C S, Wang C. 2008. Study on several key issues in nondestructive detection of bolt bonding integrity[J]. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 27(1): 108-116. |
| [8] | Li Z M. 2007. A Study on Nondestructive Detection Theory and Intelligent Diagnosis Technology of Rockbolt Anchorage Quality (in Chinese) [Ph. D. thesis]. Tianjin: School of Civil Engineering Tianjin University. |
| [9] | Liu S D, Zhang P S. 2004. The dynamic testing technology of anchoring quality for engineering anchor rod[J]. Progress in Geophysics (in Chinese), 19(3): 568-572. |
| [10] | Peng B, Liu C S, Xiao B X, et al. 2003. Signal analysis and processing of non-destructive testing data for bolt bonding integrity[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 25(3): 241-245. |
| [11] | Wang C, Yun S R, Li Y. 2000. Responding analysis for rock bolt and bonding media and surrounding rock system in instantaneous excitation[J]. Journal of Taiyuan University of Technology (in Chinese), 31(6): 658-661. |
| [12] | Wang J M, Chen Y Q, Chen H. 2004. Research on anchor bar quality nondestructive testing technique on highway[J]. Progress in Geophysics (in Chinese), 19(4): 782-785. |
| [13] | Wang J T. 2003. Wavelet analyses for stress wave detection of piles[J]. Science in China (Series E) (in Chinese), 46(2): 113-119. |
| [14] | Wang M W, Wang H L. 2001. Nondestructive testing of grouted bolts system[J]. Chinese Journal of Geotechnical Engineering, 23(1): 109-113. |
| [15] | Xu M, Zhang Y X. 2003. Numerical study of low strain dynamic test for bolt[J]. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 22(9): 1538-1541. |
| [16] | Xu M, Zhang Y X, Li Y. 2003. Analytic solution of anchor bolts with dynamic detection[J]. Journal of Chongqing Jianzhu University (in Chinese), 25(2): 48-53. |
| [17] | Yan Z X, Cai H C, Wang Q M, et al. 2011. Finite difference numerical simulation of guided wave propagation in the full grouted rock bolt[J]. Science China Technological Sciences, 54(5): 1292-1299. |
| [18] | Yang H, Wang C. 2003. Study on propagation law of elastic wave in bolt anchoring system[J]. Journal of Test and Measurement Technology (in Chinese), 17(2): 145-149. |
| [19] | Yin J M, Qin Q, Xiao G Q. 2011. Study on sonic propagation laws in anchored body of anchorage bolts with variable lengths [J]. Yangtze River (in Chinese), 42(3): 95-98. |
| [20] | Zhang C S, Li Y, Zhao Y S, et al. 2006. Study on optimum excitation wave in grout quality nondestructive testing of rock bolt[J]. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 25(6): 1240-1245. |
| [21] | Zhang D F. 2010. The Numerical Simulation Study on Dynamic Nondestructive Detection in Anchorage Quality of Rock Bolts (in Chinese) [M. S. thesis]. Zhengzhou: Zhengzhou University . |
| [22] | Zhao Y L. 2012. Study on the Ultrasonic Guided Wave Spreading in the Numerical Simulation of Bolt Anchoring System (in Chinese) [M. S. thesis]. Taiyuan: Taiyuan University of Technology . |
| [23] | Zhong H W. 2005. Propagation of Elastic Waves in Cylindrical Multilayered Solid Medium (in Chinese) [M. S. thesis]. Wuhan: China University of Geosciences. |
| [24] | Zhu G W, Peng S P, Wang H X. 2002. Test research on grouted density inspection of bolts using high frequency stress wave[J]. Rock and Soil Mechanics (in Chinese), 23(6): 787-791. |
| [25] | Zou D H S. 2004. Analysis of in situ rock bolt loading status[J]. International Journal of Rock Mechanics and Mining Sciences, 41(S1): 762-767. |
| [26] | Zuo F C. 2010. Research on Numerical Simulation of Nondestructive Test of Anchoring Quality of Rock Bolts (in Chinese) [M. S. thesis].Wuhan: Changjiang River Scientific Research Institute. |
| [27] | 雷林源, 杨长特. 1992. 桩基瞬态动测响应的数学模型及基本特性[J]. 地球物理学报, 35(4): 501-509. |
| [28] | 李维树, 甘国权, 朱容国,等. 2003. 工程锚杆注浆质量无损检测技术研究与应用[J]. 岩土力学, 24(增刊1): 189-194. |
| [29] | 李义, 张昌锁, 王成. 2008. 锚杆锚固质量无损检测几个关键问题的研究[J]. 岩石力学与工程学报, 27(1): 108-116. |
| [30] | 李张明. 2007. 锚杆锚固质量无损检测理论与智能诊断技术研究[D]. 天津: 天津大学建筑工程学院. |
| [31] | 刘盛东, 张平松. 2004. 工程锚杆锚固质量动测技术[J]. 地球物理学进展, 19(3): 568-572. |
| [32] | 彭斌, 刘春生, 肖柏勋,等. 2003. 锚杆锚固质量无损检测数据的分析与处理[J]. 物探化探计算技术, 25(3): 241-245. |
| [33] | 王成, 恽寿榕, 李义. 2000. 锚杆-锚固介质-围岩系统瞬态激励的响应分析[J]. 太原理工大学学报, 31(6): 658-661. |
| [34] | 王军民, 陈义群, 陈华. 2004. 高速公路锚杆锚固质量无损检测技术研究[J]. 地球物理学进展, 19(4): 782-785. |
| [35] | 王靖涛. 2003. 桩基应力波检测的小波分析[J]. 中国科学(E辑), 33(1): 91-96. |
| [36] | 许明, 张永兴. 2003. 锚杆低应变动测的数值研究[J]. 岩石力学与工程学报, 22(9): 1538-1541. |
| [37] | 许明, 张永兴, 李燕. 2003. 锚杆动测问题的解析解[J]. 重庆建筑大学学报, 25(2): 48-53. |
| [38] | 言志信, 蔡汉成, 王群敏,等. 2011. 导波在全长粘结锚杆中传播的有限差分数值模拟[J]. 中国科学: 技术科学, 41(5): 663-669. |
| [39] | 杨湖, 王成. 2003. 弹性波在锚杆锚固体系中传播规律的研究[J]. 测试技术学报, 17(2): 145-149. |
| [40] | 尹健民, 秦强, 肖国强. 2011. 声波在不同长度锚杆锚固体中传播规律研究[J]. 人民长江, 42(3): 95-98. |
| [41] | 张昌锁, 李义, 赵阳升,等. 2006. 锚杆锚固质量无损检测中的激发波研究[J]. 岩石力学与工程学报, 25(6): 1240-1245. |
| [42] | 张东方. 2010. 锚杆锚固质量动力无损检测数值模拟研究[D]. 郑州: 郑州大学 . |
| [43] | 赵宇亮. 2012. 超声导波在锚杆锚固体系中的传播的数值模拟[D]. 太原: 太原理工大学 . |
| [44] | 钟宏伟. 2005. 柱状多层固体介质中的弹性波传播研究[D]. 武汉: 中国地质大学. |
| [45] | 朱国维, 彭苏萍, 王怀秀. 2002. 高频应力波检测锚固密实状况的试验研究[J]. 岩土力学, 23(6): 787-791. |
| [46] | 左风春. 2010. 锚杆锚固质量声波检测的数值模拟研究[D]. 武汉: 长江科学院. |
 2015, Vol. 30
2015, Vol. 30


