传统的近区地改方法一般是选择近似规则形体去替代真实地形来进行计算，相关重力勘查技术规范中推荐了锥形、扇形、斜面、台阶等规则形体去近似测点0~20 m范围内的真实地形特征(大比例尺重力勘查规范，1997；重力调查技术规定150000，2004)，但由于山区地形、地貌特征的复杂多样，基本上是无法找到一个或多个组合的规则形体将测点近区范围内的真实地形起伏特征完全扣合在一起，因此在传统近区地改方法中不可避免地存在“人为近似”的情况，其方法本身是存在缺陷的，在实际工作中无法保证最终的地改计算精度.(朱文泉，1961；杨辉等，2000；张善法等，2009；骆迪等，2013；张国利等，2015).

基于此，本文介绍了一种基于三角网扣合的高精度近区地改算法来解决山区重力测量工作中的精度问题，该算法首先将近区划分为多个三角形区域，再分别计算出每个三角形区域对应的解析解值，最后通过累加得到高精度的重力近区地改值.三角网剖分技术善于将复杂的数值计算问题划分成任意多个简单子问题的组合，在数值计算中三角网的剖分越精细，子三角形内的计算值越精确，则最终的计算精度就越高.因此，本文高精度地改算法的核心主要是两个方面的关键问题，一个是如何在近区根据实际的地形特征合理地划分三角网，另一个是每个三角形区域所对应的地改值如何准确计算.为此，文中对这两个关键问题进行了较详细地论述，并通过算例对比，表明当三角网划分合理时，该算法的计算精度能够达到“微伽级”，对今后高精度重力测量工作具有较大的实际意义.

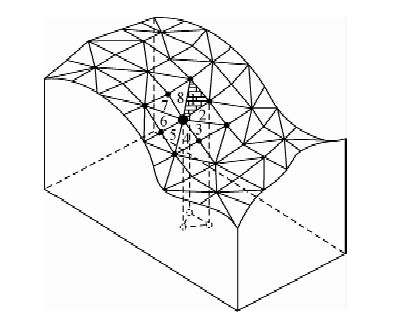
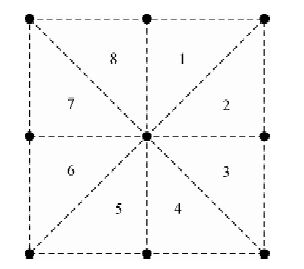
目前，三角剖分技术在地表地形建模中的应用已发展得非常成熟，将该技术应用到山区复杂地形建模中的效果示意图由图 1所示，中心大圆点表示重力实测测点，四周小圆点表示近区起伏地形上的实测高程节点，图中根据实测高程节点的空间位置，将测点周围的近区划分为8个子三角形区域，每个三角形区域在空间上是一个近似斜三棱柱体(图 1中用花纹标记)，其顶面是一个与地表地形相扣合的斜三角形，其底面是一个水平面平行的三角形，周围的三个侧面与水平面垂直.而重力近区地形改正的实质是消除地表地形起伏面与测点所在水平面之间的“质量体”在测点处产生的重力值，即按照地壳的平均密度(σ=2.67×10³ kg/m³)计算，一方面加上高于测点水平面的“质量体”在测点处产生的重力值，另一方面人为构造出一系列“质量体”去填平低于测点水平面的空间，之后加上这些“质量体”在测点处产生的重力值.将测点近区范围内的实测高程节点垂直投影到测点所在水平面上(如图 2所示)，邻近的三个投影点和与它们对应的实测高程节点一起组成了一系列的近似斜三棱柱“质量体”，累加计算出这些“质量体”在测点处产生的重力值便得到了该测点的近区地形改正值.

图 1

Fig. 1

图 1 复杂地形的三角网扣合示意图 Fig. 1 Triangulation fitting of complex topography

图 2

Fig. 2

图 2 近区的空间三角网水平投影示意图 Fig. 2 Horizontal projection of triangulation

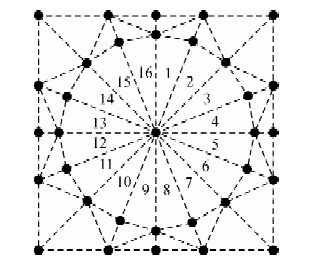
为了进一步逼近三角网与实际地形间的扣合程度，在野外实测重力测点近区周围地形起伏高程时一般从两个方面入手，一个是加密测量方位(如图 3所示，相比于图 2将测量方位加密了一倍)，另一个是加密测量方位上的实测高程节点数量(如图 4所示，相比于图 3将测量节点加密了一倍).图 4中的32个节点有很多种三角网的剖分方案，而其中的那一种是最佳的呢？经研究表明(张岭和郝天珧，2006；李振海等，2012；余杰等，2010)，Delaunay三角网具有的空圆特性和最大最小角特性，三角网中不会出现过于狭长的三角形，使得三角网的构建更加合理与准确.大量文献( 谭仁春等.2006；翁巧琳和姜昱明，2007; 郭东美，许厚泽. 2011; 尹文笋，张建中. 2014.)也对其算法的原理、实现、效果等问题进行了系统阐述，由于文章篇幅所限，不再进行赘述.

图 3

Fig. 3

图 3 加密测量方位示意图 Fig. 3 Densify measurement azimuth position

图 4

Fig. 4

图 4 加密测量节点示意图 Fig. 4 Densify measurement point

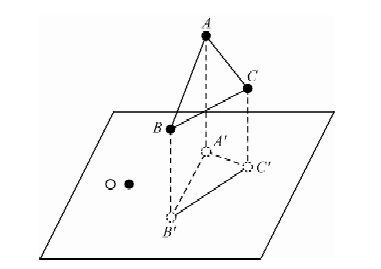
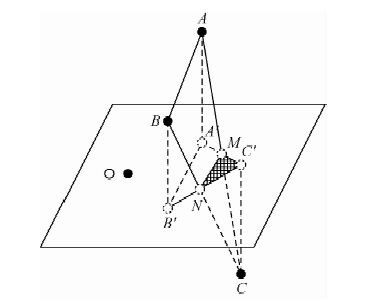
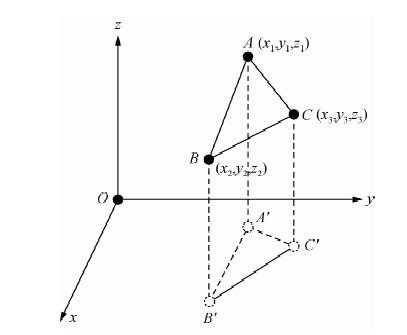
图 4中的投影节点经Delauny算法排序、组合后形成最优的Delaunay三角网，其中的三角形和与它们对应的实测高程节点一起组成了一系列最佳剖分的近似斜三棱柱“质量体”，当靠近测点O时，近似斜三棱柱体变为四面体.与图 1中的近似斜三棱柱体(图 1中用花纹标记)不同的是，近似斜三棱柱“质量体”相对于测点所在的水平面有3种空间位置关系，一种是当3个节点高程值都大于测点高程时，该近似斜三棱柱“质量体”是直立的(如图 5所示)，另一种是当3个节点高程值都小于测点高程时，该近似斜三棱柱“质量体”是倒立的，第三种是3个节点中有1个节点的相对位置与另2个节点不同时，“质量体”则变为由一个四面体和一个五面体组合而成的形体(如图 6所示，A′、B′和C′是实测高程点在测点所在水平面上的垂直投影，MN是△ABC在测点所在水平面上的交点).

图 5

Fig. 5

图 5 直立状态下的示意图 Fig. 5 Schematic diagram of erect status

图 6

Fig. 6

图 6 相交状态下的示意图 Fig. 6 Schematic diagram of intersection status

直角坐标系下，近区地改的计算公式如下，积分区域Ω表示近区范围内的起伏地形.

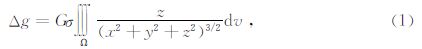
通过地表三角网的合理剖分和精细扣合，将测点近区附近的复杂地形划分成了多个近似斜三棱柱“质量体”的组合，此时(1)式可离散化如下：

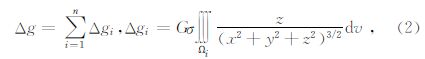
接下来需要解决的问题是如何逐个计算出单个近似斜三棱柱“质量体”对测点O产生的万有引力值.利用高斯公式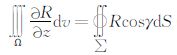(钟本善等，1989)，可将体积分转换为曲面积分，式中的γ是∑在点(x，y，z)处的法向量，由于“质量体”周围各个面的法向量是一个常量，则(2)式可变为

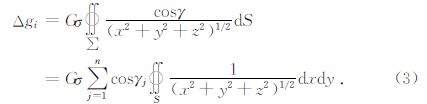
(3)式中j表示“质量体”的各个面，γ_j表示“质量体”的各个面的法向量，该式表明计算近似斜三棱柱“质量体”的体积分可以用围成“质量体”的各个面的面积分乘以各个面法向量的方向余弦求得.从图 7中可知，围成“质量体”的5个面中，三个侧面的法向量为90°，底面的法向量为0°，顶面的法向量可由顶面三角形各顶点的坐标求出，公式如下：

图 7

Fig. 7

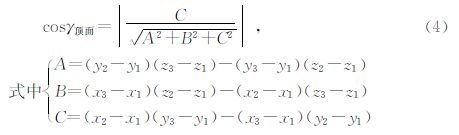
图 7 单个“质量体”的重力地改计算 Fig. 7 Gravity calculation of the single “quality”

由于三个侧面法向量的方向余弦为0，则其对应的面积分也为0，因此(3)式的计算实质是一个顶面三角形的面积分与一个底面的二重积分之和，其中近区所有“质量体”的底面二重积分累加在一起后便是积分区域为近区地改范围的二重积分Δg_底面，该二重积分是可以直接求出的，当近区地改区域为方域时，可由(5)式计算；当近区地改区域为圆域时，可由(6)式计算.

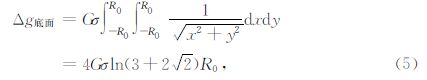
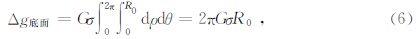
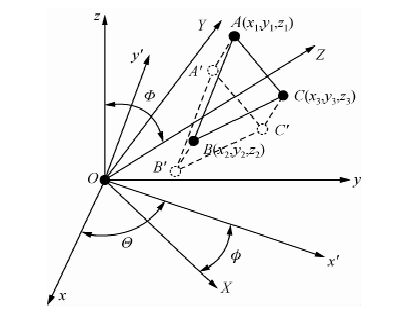
而对于顶面三角形的面积分在直角坐标系下的求解问题，M.Okabe通过坐标系旋转变换推导出了该面积分的解析解公式(Okabe，1979).如图 8所示，首先绕 z轴转动x轴和y轴，设反时针转动了θ角，使x轴方向与△ABC的外法线在xoy面的投影方向一致，再绕新y轴转动z轴和新x轴，设顺时针转动了$\phi $角使新z轴与△ABC外法线方向一致，于是在新坐标下的坐标值可由(7)式计算得到，式中x、y、z是原坐标下的坐标，X、Y、Z是新坐标下的坐标(钟本善等，1989)，公式为

图 8

Fig. 8

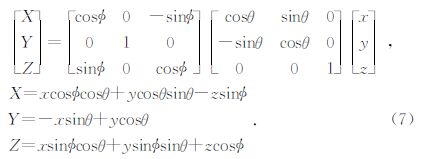
图 8 坐标系旋转示意图 Fig. 8 Coordinate system rotation’s diagram

(7)式中cos$\phi $、sin$\phi $、cosθ、sinθ均可由△ABC各点的坐标计算出来，公式为

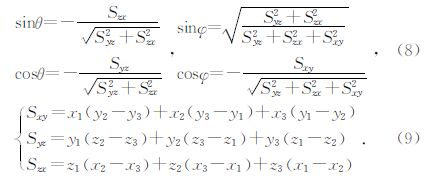
再旋转XOY平面坐标，设反时针转动了φ角，使新Y轴与某一边的外法线方向一致，得到新的坐标系εoη，在新坐标下的坐标值可由(10)式计算得到，公式为

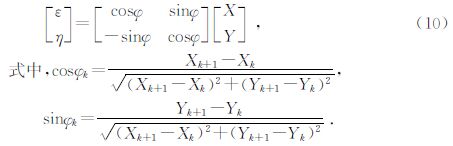
在新的坐标系εoη下，可将面积分化为线积分，即可得到：

在(11)式中，，其中：

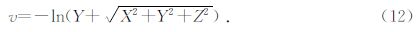
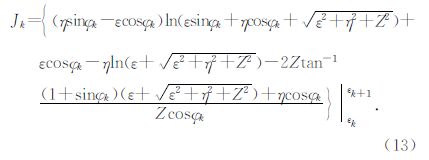
将(7)式代入到(13)式，可以得到：

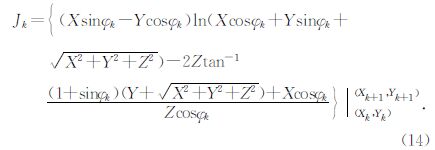
综上所述，将(10)、(14)式代入到(11)式，可得到顶面三角形的面积分Δg_{第j个顶面}.需要特别指出的是，(14)式中存在奇异值的可能，因此在计算机编程实现时需要使用“if”语句进行特殊处理.主要有三种情况：①当Z或者cosφ_k趋近于0时，将(14)式中的第二项赋值为0；②当Xcosφ_k+Ysinφ_k+$\sqrt {{X^2} + {Y^2} + {Z^2}} $趋近于0时，将(14)式中的第一项赋值为0；③当X、Y、Z都趋近于0时，将(14)式赋值为0.此外，从(3)、(5)和(6)式可知，单个“质量体”的体积分主要是与顶面三角形的面积分有关，当顶面三角形3个节点中有1个节点的相对位置与另2个节点不同时(如图 6所示)，可先求出交点M、N的坐标，再分别将△BMN、△ABN、△MNC的顶点坐标代入(7)~(14)式，最后累加求和得到Δg_{第j个顶面}.

3 算例的对比与分析

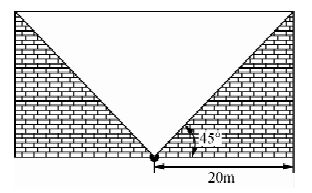
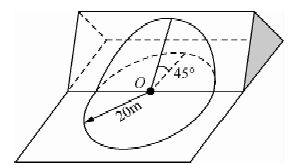
为进一步验证算法的正确性和精度，本文选择了具有精确理论解析解的漏斗模型和单斜模型进行算例对比.在算例中(如图 9、图 10所示)，将近区地改区域设置为圆域，地改半径为20 m，坡度为45°，分析不同三角网剖分情况下，算法计算结果与其解析解间的误差.

图 9

Fig. 9

图 9 漏斗模型示意图(横截面) Fig. 9 Schematic diagram of funnel model

图 10

Fig. 10

图 10 单斜模型示意图 Fig. 10 Schematic diagram of monoclinic model

漏斗模型的解析式为：Δg_漏斗=2πGσR₀(1-cosθ)，当θ=45°，R₀=20 m时，Δg_漏斗=0.655 852×10^-5 m/s².需要进一步说明的是，为表征三角网与实际地形的扣合程度，本文使用三角网的法向量与真实地形的法向量之间的差值来进行量化，计算公式为

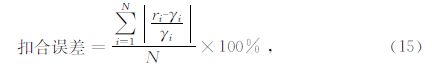
在该漏斗模型中，其任何一个子三角网所对应的真实地形法向量应为45°，其试算结果如表 1所示.从试算对比结果可知，当子三角网剖分得越细时，三角网与真实地形的扣合误差就越小，算法计算结果就越逼近其理论值.从表 1的第6列可知，本算法的计算精度达到“微伽级”，相对误差小于1%.如表 1的第5行所示，当方位数=32，环数=3时，其计算精度的数量级已小于1.0×10^-8 m/s².

表 1 (Table 1)

表 1 漏斗模型的试算对比结果 Table 1 comparative calculation results of the funnel model 序号 方位数 (M) 环数 (N) 计算值 (10-5 m/s2) 理论值 (10-5 m/s2) 绝对误差 (10-5 m/s2) 相对误差 (%) 扣合误差 (%) 1 8 1 0.662 149 0.655 852 0.006 297 0.96 4.79 2 8 2 0.662 149 0.655 852 0.006 297 0.96 4.79 3 16 1 0.657 558 0.655 852 0.001 706 0.26 1.22 4 16 2 0.657 558 0.655 852 0.001 706 0.26 1.22 5 32 3 0.656 196 0.655 852 0.000 344 0.05 0.24

表 1 漏斗模型的试算对比结果 Table 1 comparative calculation results of the funnel model

单斜模型的解析式为：Δg_单斜=πGσR₀$\left\{ {1 - \cos \theta \left[ {1 + {{\left( {\frac{1}{2}} \right)}^2}{{\sin }^2}\theta + {{\left( {\frac{{1 \times 3}}{{2 \times 4}}} \right)}^2}{{\sin }^4}\theta + \cdots } \right]} \right\}$，当θ=45°，R₀=20 m时，Δg_单斜=0.185 153×10^-5 m/s².

在该单斜模型中，其任何一个子三角网所对应的真实地形法向量为45°，其试算结果如表 2所示.由于单斜模型上的所有高程点均在同一个平面上，平面上的任意相邻的3个点便可组成一个子三角网，因此三角网与真实地形是可以完全扣合的，其扣合误差全部小于0.01%.同样地，从表 2的第6列可知，本算法的计算精度达到“微伽级”，如表 2的第6行所示，当方位数=32，环数=3时，其计算精度的数量级已小于1.0×10^-8 m/s².

表 2 (Table 2)

表 2 单斜模型的试算对比结果 Table 2 comparative calculation results of the monoclinic model 序号 方位数 (M) 环数 (N) 计算值 (10-5 m/s2) 理论值 (10-5 m/s2) 绝对误差 (10-5 m/s2) 相对误差 (%) 扣合误差 (%) 1 8 1 0.175 606 0.185 153 0.009 547 5.16 <0.01% 2 8 2 0.175 326 0.185 153 0.009 827 5.31 <0.01% 3 16 1 0.182 760 0.185 153 0.002 393 1.29 <0.01% 4 16 2 0.182 760 0.185 153 0.002 393 1.29 <0.01% 5 32 3 0.184 558 0.185 153 0.000 595 0.32 <0.01%

表 2 单斜模型的试算对比结果 Table 2 comparative calculation results of the monoclinic model

由于在实际工作中的任何一个环节均存在人为操作误差、仪器测量误差等不可避免的误差情况，因此必须从实际应用的角度出发研究本算法在测量误差情况下的试算结果.为此，在上述单斜模型的基础上，在参与计算的每个高程网格节点上加入高斯随机噪声进行试算.考虑目前实际工作中一般采用激光测距仪来进行近区高程点的测量，因此将高斯噪声的大小设置为均值为0 m、标准差为1 m，其对比计算结果如表 3所示.

表 3 (Table 3)

表 3 单斜模型的试算对比结果(高斯噪声模式下) Table 3 Comparative calculation results of the monoclinic model(under guass noise) 序号 方位数 (M) 环数 (N) 无噪计算值 (10-5 m/s2) 理论值 (10-5 m/s2) 有噪计算值 (10-5 m/s2) 无噪误差 (10-5 m/s2) 有噪误差 (10-5 m/s2) 1 8 1 0.175 606 0.185 153 0.179 729 0.009 547 0.005 424 2 8 2 0.175 326 0.185 153 0.210 645 0.009 827 0.025 492 3 16 1 0.182 760 0.185 153 0.178 073 0.002 393 0.007 08 4 16 2 0.182 760 0.185 153 0.201 713 0.002 393 0.016 56 5 32 3 0.184 558 0.185 153 0.191 382 0.000 595 0.006 229

表 3 单斜模型的试算对比结果(高斯噪声模式下) Table 3 Comparative calculation results of the monoclinic model(under guass noise)

对比表 3的试算结果可得到以下结论：①在均值为0 m、标准差为1 m的高斯测量误差情况下，其最终计算误差的数量级能达到几十微伽，本算法完全能够满足相关技术规范中所要求的精度.②在存在测量误差的情况下，单纯地增加测量节点并不意味着就能提地改计算的精度，相反地甚至可能会大大降低其计算精度，因此在野外实际工作中，应首先保证每个实测高程节点的测量精度，其次再考虑测点四周的方位数，最后用尽量少的高程节点来记录每个方位上真实地形的变化特征.③从第1、2行和3、4行的对比可知，在存在测量误差的情况下，在当方位数M一定时，在地形特征并没有发生线性变化时，人为地增加测量节点反而会大大地降低其计算精度，因此在野外记录某一方位地形变化特征时，仅仅需要测量该方位上具有明显“线性变化特征”的高程点.④当方位数=32，环数=3时，即使在高斯测量误差(均值为0 m、标准差为1 m)情况下，本算法的计算精度也能够达到“微伽级”.

综上所述，本文详细地介绍了一种基于三角网扣合的山区重力测量高精度近区地改算法，与以往方法不同的是，该算法所需的近区高程数据仅仅是测点四周的具有“线性变化”的高程节点值，不再要求技术人员必须要将周围地形特征“人为近似”到某一规则模型(如斜面、圆锥、扇形、台阶等)，从而大大地减少了工作劳动负担.而测点近区四周的“线性变化点”特征明显，在野外可以使用激光测距仪直接测量得到，因此该算法具有较强的实际应用性和推广示范性.最后，通过不同模型的试算结果表明，该算法具有较高的计算精度，在一定的高程测量误差情况下，也能够达到“微伽级”的计算精度.

致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持！