地球物理学进展  2015, Vol. 30 Issue (5): 2293-2300   PDF    
引用本文
张广智, 李振振, 赵阳, 常德宽, 印兴耀. 2015. AVF反演Q值方法研究[J]. 地球物理学进展, 30(5): 2293-2300, doi: 10.6038/pg20150542  
ZHANG Guang-zhi, LI Zhen-zhen, ZHAO Yang, CHANG De-kuan, YIN Xing-yao. 2015. The study of AVF inversion for Q value extraction. Progress in Geophysics, 30(5): 2293-2300, doi: 10.6038/pg20150542   
AVF反演Q值方法研究
张广智, 李振振 , 赵阳, 常德宽, 印兴耀    
中国石油大学(华东)地球科学与技术学院, 青岛 266580
收稿日期: 2014-08-21 修回日期: 2015-01-01.
基金项目: 国家重点基础研究发展计划"973"项目(2013CB228604,2014CB239201)、国家油气重大专项(2011ZX05014-001-010HZ)和中国石化地球物理重点实验室开放研究基金联合资助.
作者简介: 张广智,男,1971年生,中国石油大学(华东)教授,主要从事地震岩石物理、储层预测和流体识别方面的研究. (E-mail: zhanggz@upc.edu.cn)
通讯作者: 李振振,男,1989年生,中国石油大学(华东)在读硕士,主要从事储层预测和流体识别方面的研究. (E-mail: lzzwow003@163.com)
摘要: 品质因子Q的准确估计是叠前、叠后地震数据处理及AVO分析的关键环节.理论分析和正演模拟表明界面处单纯Q值的变化也会引起反射,该反射系数随频率变化而变化(Amplitude Versus Frequency, AVF).利用其线性近似公式,通过AVF反演可以准确地获得品质因子Q.AVF反演方法为Q值的求取提供了新的思路,与传统Q值求取方法不同,该方法主要考虑衰减对反射系数的影响,通过反射系数获得目的层的Q值.将上覆层为弹性介质的假设扩展到非弹性介质,构建新的近似公式,该近似公式应用更具普遍性与适应性,并利用时频分析方法获得多层模型介质的Q值；测试结果显示AVF反演的Q值准确、稳定.
关键词: AVF反演     线性近似     品质因子Q     反射系数    
The study of AVF inversion for Q value extraction
ZHANG Guang-zhi , LI Zhen-zhen , ZHAO Yang, CHANG De-kuan, YIN Xing-yao    
China University of Petroleum(Hua Dong) school of Geosciences, Qingdao 266580, China
Abstract: The accurate estimation of the quality factor Q is the key of pre-stack, post-stack seismic data processing and the AVO analysis. Theoretical analysis and forward modeling indicate that the only difference of Q value in the interface can cause reflection which changes with frequency. Based on the linear approximation formula, we can accurately obtain the quality factor Q by AVF inversion. AVF inversion provides a new idea about Q extraction. Unlike the traditional Q extraction which mainly considers the attenuation effect on the propagation wavelet, AVF inversion mainly considers the attenuation effect on the reflection coefficient, and gets the Q value of target by it. This method assumes the overlying layer elastic medium extending to non-elastic media and builds a new approximate formula. This new formula applies more universal and adaptable; besides that we get the Q value of multi-layers using the time-frequency analysis method. AVF inversion model tests show that the extraction of Q value is accurate and stable.
Key words: AVF inversion     linear approximation     the quality factor Q     reflection coefficient    
 0 引 言

随着油气勘探开发的发展，地层吸收衰减参数作为一种地震属性，在储层预测和介质物理属性反演等方面发挥着越来越重要的作用.品质因子Q作为表征介质吸收衰减性质最常用的参数，不仅在地震资料处理过程中，是估算和补偿地下介质对地震波能量吸收的重要依据，而且在预测岩性、指示油气藏位置和范围等方面发挥着越来越大的作用(Futterman，1962).因此，品质因子Q的求取在地震资料的处理与解释工作中具有重要意义.

衰减影响AVO响应的原因主要有两个方面(Bird，2012)：一是波在非弹性地层中传播，由于吸收衰减作用，波的形状、频率发生变化，主频降低，能量减小，影响AVO响应；二是衰减作为一种表征地层物理性质的参数，会直接影响反射系数.衰减通过对反射系数的影响来改变AVO响应，则理论上通过反射系数进行反演可以获取衰减参数(如品质因子Q).本文重点讨论衰减对反射系数的影响.

当平面波从弹性介质入射到粘弹介质产生反射时，波形会受粘弹介质的损耗参数所影响(White，1965).Kjartansson(1979)提出波在衰减介质中传播的数学描述，并分析了不同介质分界面上Q值对反射系数的影响.Chapman等(2006)利用基于喷射流的等效介质理论解释含烃时表现出的高衰减现象，分析了不同AVO响应时反射系数随频率变化的规律.Lines等(2008，2012)明确提出地震衰减参数差能引起反射，并随后用超声波实验证实了该说法.Quintal等(2009)基于Biot(1962)理论解释了低频地震波在流体部分饱和岩石中的衰减，数值和分析结果吻合很好.Ren(2009)利用解析方程和数个模型，研究了垂直入射衰减反射系数的特征，并根据速度频散特征将该反射系数分为三类.Innanen(2011)进一步推导了衰减反射系数，得到其关于入射角的近似公式.Bird等(2010)重点研究了品质因子Q对反射系数的影响，在假设上覆地层为弹性介质的基础上，根据Aki和Richards(2002)提出的包含常Q值的波数表达形式，得到了新的反射系数公式，该反射系数随频率变化而变化(Amplitude Versus Frequency，AVF)，利用其线性近似公式进行反演，可以得到目标层Q值与速度值.

在国内，吴小羊(2010)、张世鑫等(2011)、程冰洁等(2012)、郝前勇等(2013)、张震等(2014)等讨论了粘弹介质中由于速度频散引起的频变反射系数，并且反演得到相关的频散属性参数；但没有进一步考虑影响速度频散的参数(品质因子等)对反射系数的影响.刘财等(2007)利用伪谱技术模拟粘弹各向异性介质分界面上波的反射与透射，并与弹性各向异性介质、粘弹各向同性介质和弹性各向同性介质的模拟做比较，得出粘弹介质分界面上的反射透射不仅与界面两侧速度对比有关，还与品质因子Q对比有关的结论.郭智奇等(2010)研究了盖层为衰减各向异性对AVO分析的影响，指出在进行AVO分析之前必须对衰减各向异性加以校正.沈章洪和王小杰(2013)将粘弹介质精确Zoeppritz方程进行简化，并利用四类AVO典型界面模型进行分析，为粘弹性近似式的应用提供了理论指导.罗亨和王华忠(2014)根据相速度与Q值的关系得到了直接由Q表示的反射系数，并提出了Q阻抗的概念.

子波的变化、随机噪声等因素将影响AVF反演的结果，Bird利用最小平方法进行AVF反演，取得了稳定准确的反演结果.

1 衰减反射系数

通常认为地震反射是由阻抗差异引起的.然而，在地震能量明显衰减的介质中，吸收系数α(品质因子Q)的差异也能引起反射.

当平面波从一衰减均质层垂直入射到另一衰减均质层时，反射系数可以写为

其中R是反射系数，kz0是上覆层的垂向波数，kz1是目标层的垂向波数.为了构建衰减反射系数，利用Aki和Richards(2002)提出的包含常数Q值的波数表达式为
其中Q为品质因子，ω为角频率，ωr为参考频率，c是频率为ωr时的相速度.将其代入(1)式可得：
R(ω)即为衰减反射系数.

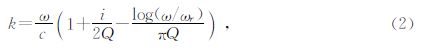
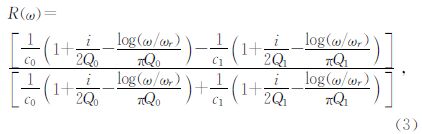
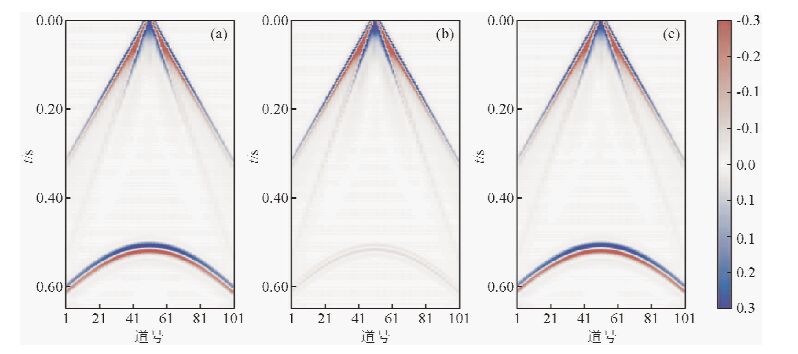
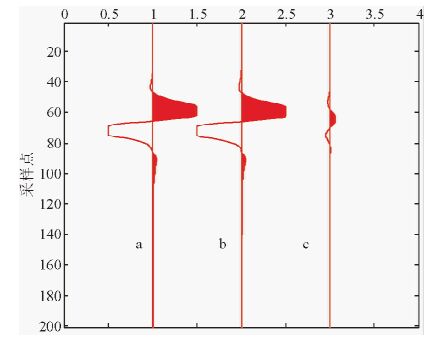
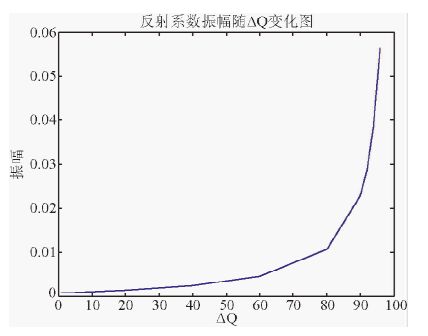
下面通过建立双层模型验证上述理论(图 1).图(a)中上下两层介质只有速度有差别，图(b)中上下两层介质只有Q值有差别，图(c)上下两层介质速度和Q值都有差别.震源在0处激发，利用有限差分正演模拟，得到合成地震记录(图 2).从图 2b中可以看出，单独的Q值变化也能引起反射.为了分析两种反射系数之间的关系，抽取零偏移距地震道(图 3)，图 3a是图 2c中的零偏移距地震道，图 3b是图 2a、图 2b的零偏移距地震道之和，图 3c是图 3a和图 3b的差.从图 3c中可以直观的看出，同时具有波阻抗差和Q值差异时，二者对反射系数的影响并不是简单的叠加关系.图 4是零炮检距反射系数振幅随上下两层介质Q差(ΔQ)变化图.从图 4可以看出，ΔQ对反射系数的影响也不是线性的.

图 1 地层模型
(a)只有速度差异的双层模型；(b)只有品质因子差异的双层模型；(c)速度和品质因子都有差异的双层模型. Fig. 1 Stratigraphic Modeling
(a)Bilayer model with only velocity difference;(b)Bilayer model with only Q value difference; (c)Bilayer model with velocity and Q value difference.

图 2 模型数据正演得到的炮记录
(a)(b)(c)是与图 1模型中(a)(b)(c)相对应的地震正演记录(色标均相同) Fig. 2 Shot Records from forward model
(a)(b)(c)correspond to the model(a)(b)(c)in Fig 1(the color bar are same)

图 3 零偏移距地震记录对比及差异 Fig. 3 The comparison and differences of zero-offset seismic records

图 4 反射系数振幅随ΔQ变化而变化 Fig. 4 The amplitude of the reflection coefficient changes with the ΔQ
2 最小平方AVF反演

假设上覆层为弹性介质(Q0→∞)，由(3)式得：

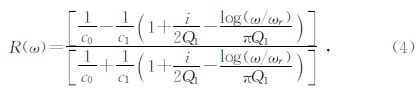
令，可得：
在c0<$\sqrt 2 $c1的条件下将$\sqrt {1 - ac} $进行泰勒展开，可得：
其中，Ψ= (－$\frac{1}{2}$aQF(ω)+$\frac{1}{4}$aC+$\frac{1}{4}$aCaQF(ω)+…) .将R(ω)= $\frac{\psi }{{1 - \psi }}$进一步泰勒展开可得：
假设aQ和aC很小可得线性公式为
将上覆层为弹性地层的假设扩展到非弹性层时，重新推导近似公式可得参数aQ为(见附录):
可以看出，aQ= $\frac{1}{{{Q_1}}}$是(9)式在上覆层为弹性介质(Q0→∞)时的近似.

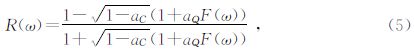
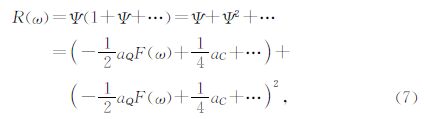
(8)式可以用矩阵形式表示为

考虑子波的影响，方程(8)可以进一步写为
其中，W(ω)为子波的频谱，S(ω，θ)为反射系数与子波的乘积.方程(11)可以用矩阵形式表示为
用阻尼最小二乘法反演出aC和aQ后，即可得到目标层的Q值与纵波速度.

3 模型测试

首先利用图 1中的模型对线性近似公式的准确性及反演效果进行测试.

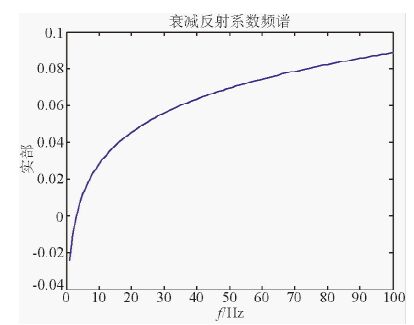
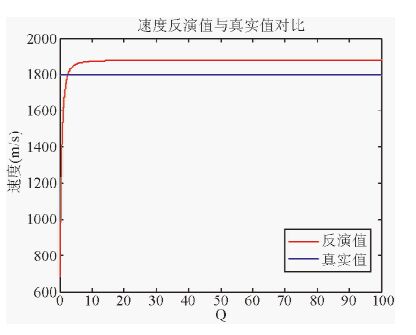
图 5是目标层Q值为5的衰减反射系数频谱，从图中可以看出衰减反射系数随频率变化而变化；图 6是精确衰减反射系数、Bird线性近似和本文提出的线性近似的频谱对比图，图 7是上覆层Q值为50时反演得到的纵波速度值与真实值的比较，图 8同样是上覆层Q值为50时反演得到的Q值与真实值的比较.图 6中(a)(b)上覆层的Q值分别为50和1000，结果表明当上覆层Q值足够大时，两种近似公式基本一致；当上覆层Q值较小时，本文提出的近似公式精确度高.从图 8中可以明显的看出，当Q值很小时，反演结果不好，这是因为线性化近似的结果；当Q值足够大时，反演结果与真实值相差很小，表明了反演的准确性.

图 5 衰减反射系数频谱实部 Fig. 5 The real part of the Attenuation reflection coefficient spectrum

图 6 衰减反射系数频谱及两种线性近似 Fig. 6 The spectrum of attenuation reflection coefficient and two linear approximation

图 7 反演速度及其真实速度 Fig. 7 Inverted and real velocity

图 8 反演Q值及其真实Q值
(a)Q值从0到10；(b)Q值从10到100. Fig. 8 Inverted and real Q value
(a)Q is from 0 to 10;(b)Q is from 10 to 100.

在多层介质情况下，近似公式反演得到的Q值有误差累加效应，为此建立多层模型，参数如表 1所示，添加不同程度的噪声，测试反演效果的稳定性及抗噪性.

表 1 模型参数 Table 1 Model parameters

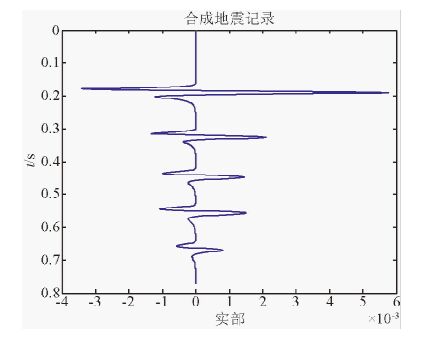
图 9为合成地震记录，图 10为该合成地震记录的时频谱.图 11~14分别是加不同噪声时，反演值与真实值的对比.从图中可以看出，随着信噪比(SNR)降低，反演的Q值准确性有所降低，但即使信噪比较低(SNR=2)的情况下，Q值的反演误差仍然很小.这证明了AVF反演Q值稳定性好，抗噪性强.

图 9 合成地震记录 Fig. 9 Synthetic seismogram

图 10 合成地震记录时频谱 Fig. 10 The spectrum of synthetic seismogram

图 11 不加噪声，Q的反演值和真实值对比 Fig. 11 Inverted and real Q without noise

图 12 SNR=10，Q的反演值和真实值对比 Fig. 12 Inverted and real Q with SNR=10

图 13 SNR=4，Q的反演值和真实值对比 Fig. 13 Inverted and real Q with SNR=4

图 14 SNR=2，Q的反演值和真实值对比 Fig. 14 Inverted and real Q with SNR=2

图 15和图 16分别是Marmousi2模型的纵波速度与Q值，其中Q值根据李氏经验公式(1994)由纵波速度得到，可以看出含气区Q值较小，衰减严重.图 17和图 18分别为反演的速度值与Q值.从图中可以看出反演Q值在含气处(红框指示位置)显示明显低值，与原始模型对应良好，反演精度符合要求.

图 15 Marmousi2模型速度值 Fig. 15 The velocity of Marmousi2 model

图 16 Marmousi2模型Q值 Fig. 16 The Q value of Marmousi2 model

图 17 反演速度值 Fig. 17 Inverted velocity

图 18 反演Q值 Fig. 18 Inverted Q value
4 结论与讨论

理论分析和数据模拟结果表明，Q值差异会引起与频率有关的反射，而利用最小平方AVF反演能够稳定准确的估测该Q值差异.AVF反演为Q值求取提供了新的方法与思路.在实际数据处理中，因涉及时变子波提取、反射系数求取等问题，在此未多做介绍.时频分析方法的应用在反演中起到重要的作用，非平稳反褶积等求取衰减反射系数的方法是以后重点研究内容之一；另外由于Q值差异引起的反射与波阻抗差异引起的反射相比要小的多，实际资料中如何有效辨别波阻抗差还是Q值差引起的反射也需要做进一步研究.

致 谢 感谢中石化石油勘探开发研究院项目“基于叠前属性分析的碳酸盐岩缝洞储层反演方法研究”，中海油项目“渤中1/2区叠前处理、储层反演与有利储层预测”对本文研究的支持和资助.

附录

参数 a Q=$\frac{1}{{{Q_1}}} - \frac{1}{{{Q_0}}}$的推导

令aC=1-$\frac{{c_0^2}}{{c_1^2}}$，根据公式(5)可得

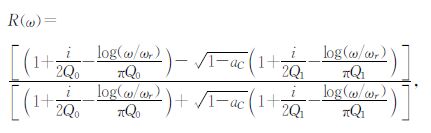
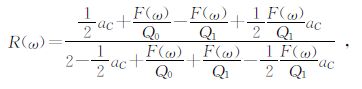
令F(ω)=$\frac{i}{2} - \frac{{\log \left( {\omega /{\omega _r}} \right)}}{\pi }$且在aC∈(-1，1)即c0< $\sqrt 2 $c1的条件下，将$\sqrt {1 - ac} $进行泰勒展开可得
令$\Omega = \frac{1}{4}ac - \frac{{F\left( \omega \right)}}{{2{Q_1}}} + \frac{1}{4}\frac{{F\left( \omega \right)}}{{{Q_1}}}ac,\psi = \Omega - \frac{{F\left( \omega \right)}}{{2{Q_0}}}$，则有$R\left( \omega \right) = \frac{{\psi + \frac{{F\left( \omega \right)}}{{{Q_0}}}}}{{1 - \psi }}$
再次进行泰勒展开，可得
若令aQ=$\frac{1}{{{Q_1}}} - \frac{1}{{{Q_0}}}$则反射系数仍可以写为R(ω)≈-$\frac{1}{2}$aQF(ω)+$\frac{1}{4}$ aC.

参考文献
[1] Aki K, Richards P G. 2002. Quantitative Seismology [M]. 2nd ed. California: University Science Books, 4-5.
[2] Biot M A. 1962. Mechanics of deformation and acoustic propagation in porous media [J]. Journal of Applied Physics, 33(4): 1482-1498.
[3] Bird C, Innanen K, Lines L, et al. 2010. Determination of anelastic reflectivity: how to extract seismic AVF information [R]. CREWES Research Report, volume 22.
[4] Bird C, Innanen K, Naghizadeh M. 2011. Least squares AVF inversion [R]. CREWES Research Report, volume 23.
[5] Bird C. 2012. Amplitude-variation-with frequency (AVF) analysis of seismic data over anelastic targets [D]. Alberta: University of Calgary.
[6] Chapman M E, Liu E R, Li X Y. 2006. The influence of fluid-sensitive dispersion and attenuation on AVO analysis [J]. Geophysical Journal International, 167(1): 89-105.
[7] Cheng B J, Xu T J, Li S G. 2012. Research and application of frequency dependent AVO analysis for gas recognition [J]. Chinese J. Geophys. (in Chinese), 55(2): 608-613, dio: 10.6038/j.issn.0001-5733.2012.02.023.
[8] Futterman W I. 1962. Dispersive body waves [J]. Journal of Geophysical Research, 67(13): 5279-5291.
[9] Guo Z Q, Liu C, Feng X, et al. 2010. Attenuation anisotropy and AVO analysis[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 40(2): 432-438.
[10] Hao Q Y, Zhang S X, Zhang F, et al. 2013. Dispersion attributes estimation based on frequency-dependent AVO inversion and its application in hydrocarbon detection [J]. Oil Geophysical Prospecting (in Chinese), 48(2): 255-261.
[11] Innanen K A. 2011. Inversion of the seismic AVF/AVA signatures of highly attenuative targets [J]. Geophysics, 76(1): R1-R14.
[12] Kjartansson E. 1979. Attenuation of seismic waves in rocks and applications in energy exploration [D]. California: Stanford University.
[13] Lines L, Vasheghani F, Treitel S. 2008. Reflections on Q [C].// CSEG Recorder, 36-38.
[14] Lines L, Innanen K, Vasheghani F, et al. 2012. Experimental Confirmation of “Reflections on Q” [C].// SEG 2012 Annual Meeting.
[15] Liu C, Guo Z Q, Yang B J, et al. 2007. Analysis of reflection and transmission problems of waves in viscoelastic anisotropic media [J]. Chinese J. Geophys. (in Chinese), 50(4): 1216-1224.
[16] Quintal B, Schmalholz S M, Podladchikov Y Y. 2009. Low-frequency reflections from a thin layer with high attenuation caused by interlayer flow [J]. Geophysics, 74(1): N15-N23.
[17] Ren H T, Goloshubin G, Hilterman F J. 2009. Poroelastic analysis of amplitude-versus-frequency variations [J]. Geophysics, 74(6): N41-N48.
[18] Shen Zhang-Hong, Wang Xiao-Jie. 2013. The approximation of P waves reflection and transmission coefficient in viscoelastic medium and comparative analysis [J]. Progress in Geophys. (in Chinese), 28(1): 257-264, doi: 10.6038/pg20130127.
[19] White J E. 1965. Reflections from lossy media [J]. The Journal of the Acoustical Society of America, 38(4): 604-607.
[20] Zhang Z, Yin X Y, Hao Q Y. 2014. Frequency-dependent fluid identification method based on AVO inversion[J]. Chinese J. Geophys. (in Chinese), 57(12): 4171-4184, dio: 10.6038/cjg20141228.
[21] 程冰洁, 徐天吉, 李曙光. 2012. 频变AVO含气性识别技术研究与应用[J]. 地球物理学报, 55(2): 608-613, dio: 10.6038/j.issn.0001-5733.2012.02.023.
[22] 郭智奇, 刘财, 冯晅,等. 2010. 各向异性衰减与AVO分析[J]. 吉林大学学报(地球科学版), 40(2): 432-438.
[23] 郝前勇, 张世鑫, 张峰,等. 2013. 基于频变AVO反演的频散属性估算方法及其应用[J]. 石油地球物理勘探, 48(2): 255-261.
[24] 李庆忠. 1994. 走向精确勘探的道路——高分辨率地震勘探系统工程剖析[M]. 北京: 石油工业出版社, 31-44.
[25] 刘财, 郭智奇, 杨宝俊,等. 2007. 黏弹各向异性介质中波的反射与透射问题分析[J]. 地球物理学报, 50(4): 1216-1224.
[26] 罗亨, 王华忠. 2014. 粘弹性介质中AVAF方程和Q阻抗[C].// CPS/SEG北京2014国际地球物理会议: 195-198.
[27] 沈章洪, 王小杰. 2013. 粘弹性介质P波反射透射系数近似及对比分析[J]. 地球物理进展, 28(1): 257-264, doi: 10.6038/pg20130127.
[28] 吴小羊. 2010. 基于频谱分析技术的频散AVO反演研究[D]. 武汉: 中国地质大学(武汉).
[29] 张世鑫, 印兴耀, 张广智,等. 2011. 纵波速度频散属性反演方法研究[J]. 石油物探, 50(3): 219-224.
[30] 张震, 印兴耀, 郝前勇. 2014. 基于AVO反演的频变流体识别方法[J]. 地球物理学报, 57(12): 4171-4184, dio: 10.6038/cjg20141228.