2. 华北油田地球物理勘探研究院, 任丘 062552
2. Geophysical Exploration Research Institute of PetroChina Huabei Oilf ield Company, Renqiu 062552, China
地震属性是指从地震数据中导出的关于运动学、动力学及统计特性的特殊度量值.目前,在常用的地震解释软件中,可以提取的地震属性已达40多种(孟召平等,2006).近年来,又发展出一些新的地震属性(李春峰和Christopher,2005; 邵锐等,2011),其中曲率属性在国外地球物理界受到广泛青睐,由于该属性增加了多波长和三维可视化解释功能,地质效果明显.Roberts利用3×3平面网格拟合曲面计算曲率(Roberts,2001; 李福强等,2012; 2013),并给出了详细的计算公式,使得曲率属性成为地震解释的一大亮点;休斯顿大学应用物理实验室的Marfurt等人(Hakami et al.,2004; Marfurt,2006)在 Roberts 研究的基础上,将它推广到沿层曲率属性的提取; Gao Dengliang(Gao,2013; Di and Gao,2014)提出了梯度曲率属性,并将其用于小断层识别;王世星(王世星,2012),印兴耀(Gao et al.,2014; 印兴耀等,2014)等人给出了一种基于倾角扫描的体曲率提取方法;Qi Jie(Qi et al.,2014)给出了断层控制的卡斯特地区的曲率属性特征.
在曲率属性的计算过程中,采用不同的网格对二次曲面进行拟合求得的曲率计算精度和效果是不同的.对于一些小断层和微幅构造的识别成为目前地震资料解释的重点和难点之一.而曲率属性作为一种识别断层和微幅构造的常用手段,其精度也必须有所提高.所以,本文在前人研究的基础上提出了用5×5网格来拟合二次曲面以期得到更高精度的曲率属性,并将其权系数表达成微分算子的形式来提高其运算效率.实际资料表明,5×5网格下的曲率属性比3×3网格下求取的曲率属性在裂缝识别方面的效果更好.
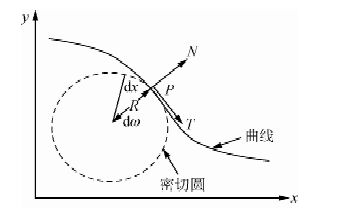
1 方法原理 1.1 曲率的定义高等数学对曲线的曲率定义为:曲率是单位弧段上切线转过角度大小的极限(图 1).
|
图 1 曲率的数学定义 Fig. 1 The mathematical definition of curvature |
据此,导出圆的曲率为

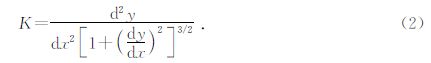
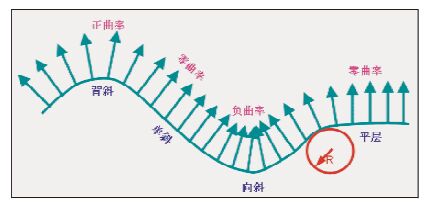
将曲率的概念引入构造解释中,就可以定量的描述构造特征,图 2 给出了背斜、单斜、向斜、平层和断层的曲率描述.其中,背斜的曲率为正,向斜的曲率为负;平层和单斜层的曲率为零;断层在平滑后可以近似地认为其曲率具有正到负或负到正的变化(张军华等,2009).在实际工作中要使解释结果能更加真实的反映地下构造尤其是裂缝、孔洞等微小复杂构造时必须借助针对空间曲面上进行的二维曲率分析结果(AI-Dossary and Marfurt,2006; 王雷等,2010; 方海飞等,2013).
|
图 2 不同构造的曲率 Fig. 2 The curvature of the different structure |
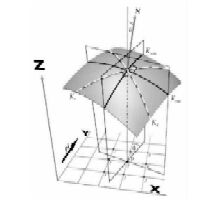
将曲率的2D概念推广到3D情况,Roberts给出了一个很形象化的描述:如图 3所示,假设一个层面是一个苹果的表皮,而数学上的平面是一把刀.刀切过苹果表皮的切口代表曲线.把苹果的顶部切掉得到一个非常小的圆周,因此它的曲率非常大.当然可以切无穷多个切面,因此可以得到无穷多个曲率.其中,那些正交于层面的平面所定义的曲率称为法曲率(Roberts,2001).
|
图 3 曲面的法曲率示意图 Fig. 3 The schematic diagram of normal curvature of the surface |
对于二维曲面的拟合公式:
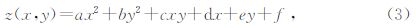
|
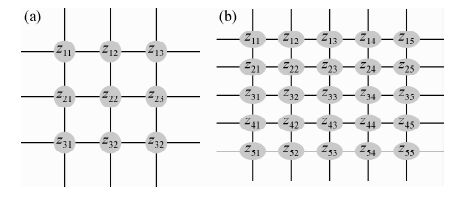
图 4 二次曲面拟合计算网格 (a)3×3 网格;(b)5×5 网格. Fig. 4 Quadric surface fitting of computational grid (a)3×3grid;(b)5×5grid. |
以Roberts的推导思路为基础,应用中心差分方法计算空间导数,并表示成微分算子模板形式(刘玉和朱耀庭,1985; 杨威,2011; 杨威等,2011),其权系数矩阵为
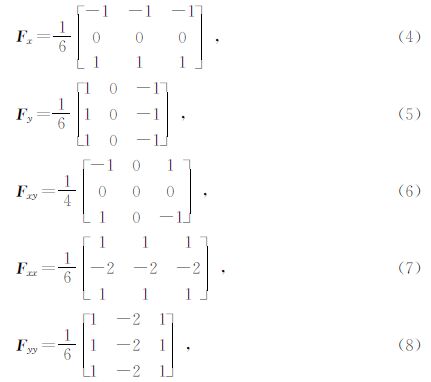


基于以上中心差分的求解思路,对5×5 网格进行推导,得到以下权系数矩阵为

同理,也可得到对应的系数a,b,c,d,e.
1.3 各种曲率属性的计算公式根据不同曲率属性的定义,目前,可以计算得到的曲率属性有十多种(李澈等,2014).根据不同属性对不同构造的检测效果,以及针对本文所用工区的实际资料的应用效果综合分析,选取最小负曲率和极大曲率两种属性进行分析.现给出其计算公式以及地质意义:
(1)最小负曲率
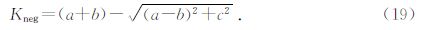
法曲率中最小的负曲率称为最小负曲率.该曲率能放大层面中的断层信息和一些小的线性构造(张军华等,2009).
(2)极大曲率

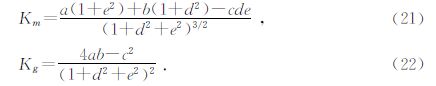
层面上某一点的无穷多个正交曲率中存在一曲线,该曲线的曲率为极大,此曲率称为极大曲率.断层表现为正曲率值和负曲率值的邻接,曲率值确定了断层的错断方向,正的曲率值代表上升盘,负的曲率代表下降盘.Sigismundi和Soldo(2003)认为最大曲率数据的时间切片上很容易看出断块的相对运动(李澈等,2014).极大曲率可以用来检测断层及构造的边缘,实际证明效果良好.
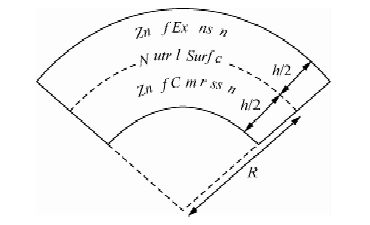
1.4 曲率和应力的关系如图 5所示,当地层发生弯曲时,顶部拉伸增强,底部压缩增强,中立面无应力.地层顶部的应力计算公式为

|
图 5 地层弯曲时应力示意图 Fig. 5 Diagram of the crustal stress |
地层在沉积过程中,由于构造运动使地层发生褶皱或弯曲以及其他更为复杂的形变.当地层发生这些变化时,由于应力差异的存在就会产生断层以及几何形状复杂的裂缝(孔选林等,2011).由于曲率和应力之间又存在密切的关系,因此,可以运用曲率属性来对断层和裂缝进行识别和预测(王雷等,2010; 宋建国等,2013).
2 应用实例 2.1 实际应用效果渤南油田区域构造上位于济阳坳陷沾化凹陷中部的渤南洼陷内,北与埕东凸起以大断层相接,东与孤岛油田相邻.本文的研究区块为渤南五区,五区位于渤南油田的东南部,南北被两条近东西走向的大断层所切割,东西两侧受岩性控制,是一个受岩性和构造控制的构造岩性油藏.前文提到曲率和应力之间存在密切关系,对工区进行了地应力模拟,结果表明:工区西部地应力方向为北偏东120°;该地区断层和裂缝发育,走向以东西向为主.由于曲率与层面的二阶导数密切相关,对噪声相当敏感,故压制层面噪声极其重要,为了减少层位数据的噪声对曲率属性计算的负面影响,采用二维高斯滤波模板进行加权平滑滤波.
根据各种曲率的计算方法,对某工区的层位t2,选取Kneg、Kmax两种曲率,分别应用3×3、5×5网格对曲面进行拟合后进行计算,得到三种曲率属性如下:
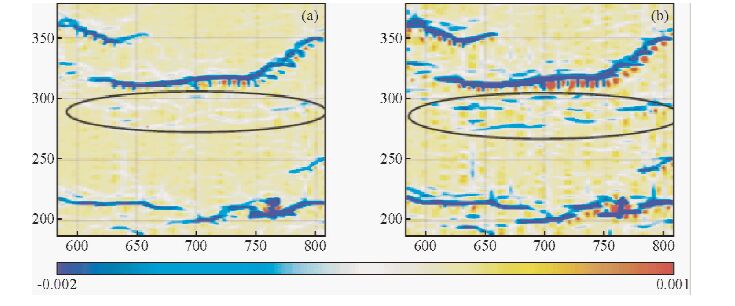
如图 6中椭圆表示的区域所示:对于属性Kneg,随着网格点数的增加,曲率的精度得到了极大提高,属性切片上表示裂缝和断层线更加粗深,使小断层更易于识别,一些小的裂缝更加明显地显示出来.且图中断层和裂缝的走向以东西向为主,与前期研究结果相吻合.
|
图 6 t2层位Kneg属性沿层切片 (a)3×3网格拟合结果;(b)5×5网格拟合结果. Fig. 6 The Kneg slice of the t2 horizon (a)The result of 3×3grid;(b)The result of 5×5 grid. |
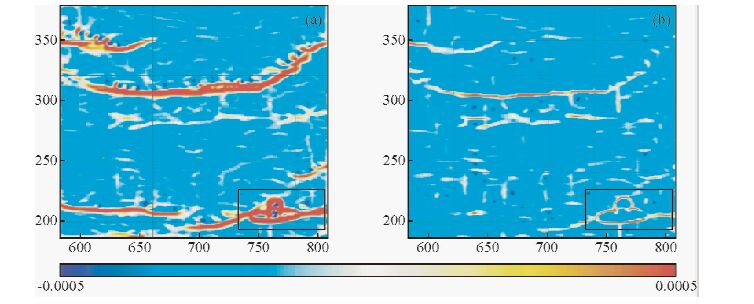
对于属性Kmax,通过5×5网格拟合结果与3×3网格拟合结果的对比分析可以看出,在工区的东南角(图 7方框内)构造间的关系、轮廓更细致,构造的边界更清晰.
|
图 7 t2层位Kmax属性沿层切片 (a)3×3网格拟合结果;(b)5×5网格拟合结果. Fig. 7 Kmax slice of the t2 horizon (a)The result of 3×3grid;(b)The result of 5×5 grid. |
本文所用工区面积约为30 km2,地震数据大小约为450 M.对本工区用不同网格进行拟合并求取Kneg和Kmax的时间进行统计,得到结果如下表:
|
|
表 1 用不同网格单元提取曲率所用时间 Table 1 The time of different grid units used to extract curvature attributes |
由上表可以看出,5×5网格拟合求取曲率的运行时间和3×3网格的运行时间相差大概在1 s左右,计算量增加并不是很多,因此,用5×5网格拟合曲面来求取曲率属性还是很有现实意义的.
3 结 论通过对曲率计算公式进行3×3网格和5×5网格拟合对比发现,对不同的曲率属性改进的效果也不尽相同:对于属性Kneg,随着网格点数的增加,表示裂缝和断层线更加粗深,使小断层和裂缝更易于识别;对于属性Kmax,5×5网格拟合结果对于断层、构造边界及相互间关系的刻画更细致.因此,5×5网格下拟合的曲率属性在精度方面还是有一定程度的提高的,同时,其计算效率也在可接受的范围内.所以,用5×5网格来拟合二次曲面求曲率是具有实际意义的.
致 谢 本研究得到了《井数据驱动的高精度地震处理关键技术》项目的资助,在此表示诚挚的感谢,同时感谢各位审稿专家和编辑部的各位老师的指导与帮助.
| [1] | AI-Dossary S, Marfurt K J. 2006. 3D volumetric multispectral estimates of reflector curvature and rotation[J]. Geophysics, 71(5): P41-P51. |
| [2] | Di H B, Gao D L. 2014. A new analytical method for azimuthal curvature analysis from 3D seismic data [C].// Paper presented at the SEG Technical Program Expanded Abstracts 2014. Denver, Colorado, USA: SEG, 1634-1638. |
| [3] | Fang H F, Zhou S, Wang Y L, et al. 2013. Geometric attribute improved-processing in fault interpretation [J]. Oil Geophysical Prospecting (in Chinese), 48(S1): 120-124. |
| [4] | Gao D L. 2013. Integrating 3D seismic curvature and curvature gradient attributes for fracture characterization: Methodologies and interpretational implications[J]. Geophysics, 78(2): O21-O31. |
| [5] | Gao J H, Yin X Y, Zong Z Y. 2014. Curvature attribute based on dip scan with eccentric window [C].// Paper presented at the SEG Technical Program Expanded Abstracts 2014. SEG, 1614-1618. |
| [6] | Hakami A M, Marfurt K J, Al-Dossary S. 2004. Curvature attribute and seismic interpretation: Case study from Fort Worth Basin, Texas, USA [C].// Paper presented at the SEG Technical Program Expanded Abstracts 2004. SEG, 544-547. |
| [7] | Kong X L, Tang J M, Xu T J. 2011. Application of seismic curvature attribute to fracture prediction in Xinchang area, Western Sichuan Depression [J]. Geophysical Prospecting for Petroleum (in Chinese), 50(5): 517-520. |
| [8] | Li C, Ji T Y, Li Y C. 2014. Analysis of curvature attribute and its application in seismic interpretation [J]. Contemporary Chemical Industry (in Chinese), 43(4): 558-560. |
| [9] | Li C F, Christopher L. 2005. Singularity exponent from wavelet-based multiscale analysis: A new seismic attribute[J]. Chinese Journal of Geophysics (in Chinese), 48(4): 882-888. |
| [10] | Li F Q, He Z H, Wen X T, et al. 2012. An improved curvature calculation algorithm and its effect analysis[J]. Geophysical Prospecting for Petroleum (in Chinese), 51(2): 146-150. |
| [11] | Li F Q, Jiang W J, Cai H P, et al. 2013. New curvature calculation formula and its application[J]. Coal Geology & Exploration (in Chinese), 41(2): 83-86. |
| [12] | Liu Y, Zhu Y T. 1985. Surface fitting-the laplacian method in edge detection[J]. Journal of Huazhong Institute of Technology (in Chinese), 13(4): 39-46. |
| [13] | Marfurt K J. 2006. Robust estimates of 3D reflector dip and azimuth[J]. Geophysics, 71(4): P29-P40. |
| [14] | Meng Z P, Guo Y S, Wang Y, et al. 2006. Prediction models of coal thickness based on seismic attributions and their applications[J]. Chinese Journal of Geophysics (in Chinese), 49(2): 512-517. |
| [15] | Qi J, Zhang B, Zhou H L, et al. 2014. Attribute expression of fault-controlled karst-Fort Worth Basin, TX [C].// Paper presented at the SEG Technical Program Expanded Abstracts 2014. Denver, Colorado, USA: SEG, 1522-1527. |
| [16] | Roberts A. 2001. Curvature attributes and their application to 3D interpreted horizons[J]. First Break, 19(2): 85-100. |
| [17] | Shao R, Sun Y B, Yu H S, et al. 2011. Identification technology of volcanic edifice based on seismic attribute anisotropy[J]. Chinese Journal of Geophysics (in Chinese), 54(2): 343-348, doi: 10.3969/j.issn.0001-5733.2011.02.010. |
| [18] | Song J G, Sun Y Z, Ren D Z. 2013. Edge detection technique based on structure-directed gradient attribute[J]. Chinese Journal of Geophysics (in Chinese), 56(10): 3561-3571, doi: 10.6038/cjg20131031. |
| [19] | Wang L, Chen H Q, Chen G W, et al. 2010. Application of curvature attributes in predicting fracture-developed zone and its orientation [J]. Oil Geophysical Prospecting (in Chinese), 45(6): 885-889. |
| [20] | Wang S X. 2012. High-precision calculation of seismic volumetric curvature attributes and its applications [J]. Oil Geophysical Prospecting (in Chinese), 47(6): 965-972. |
| [21] | Wen W, Wen X T. 2011. Application of curvature in complex geological detection [J]. Journal of Oil and Gas Technology (in Chinese), 33(7): 84-87. |
| [22] | Yang W. 2011. Analysis of curvature attribute and its application[D] (in Chinese). Chengdu: Chengdu University of Technology. |
| [23] | Yang W, He Z H, Chen X H. 2011. Application of structure-oriented filtering to volumetric curvature calculation [J]. Geophysical Prospecting for Petroleum (in Chinese), 50(1): 27-32. |
| [24] | Yin X Y, Gao J H, Zong Z Y. 2014. Curvature attribute based on dip scan with eccentric window [J]. Chinese Journal of Geophysics (in Chinese), 57(10): 3411-3421, doi: 10.6038/cjg20141027. |
| [25] | 方海飞, 周赏, 王永莉,等. 2013. 几何类属性深度处理技术在断层解释中的应用[J]. 石油地球物理勘探, 48(S1): 120-124. |
| [26] | 孔选林, 唐建明, 徐天吉. 2011. 曲率属性在川西新场地区裂缝检测中的应用[J]. 石油物探, 50(5): 517-520. |
| [27] | 李澈, 季天愚, 李雨澈. 2014. 曲率属性分析及其在地震资料解释中的应用[J]. 当代化工, 43(4): 558-560. |
| [28] | 李春峰, Christopher L. 2005. 基于小波多尺度分析的奇性指数: 一种新地震属性[J]. 地球物理学报, 48(4): 882-888. |
| [29] | 李福强, 贺振华, 文晓涛,等. 2012. 改进的曲率计算方法及其效果分析[J]. 石油物探, 51(2): 146-150. |
| [30] | 李福强, 蒋文杰, 蔡涵鹏,等. 2013. 曲率计算公式的改进及应用效果[J]. 煤田地质与勘探, 41(2): 83-86. |
| [31] | 刘玉, 朱耀庭. 1985. 边界检测中的曲面拟合-拉普拉斯算子法[J]. 华中工学院学报, 13(4): 39-46. |
| [32] | 孟召平, 郭彦省, 王趕,等. 2006. 基于地震属性的煤层厚度预测模型及其应用[J]. 地球物理学报, 49(2): 512-517. |
| [33] | 邵锐, 孙彦彬, 于海生,等. 2011. 基于地震属性各向异性的火山机构识别技术[J]. 地球物理学报, 54(2): 343-348. |
| [34] | 宋建国, 孙永壮, 任登振. 2013. 基于结构导向的梯度属性边缘检测技术[J]. 地球物理学报, 56(10): 3561-3571. |
| [35] | 王雷, 陈海清, 陈国文,等. 2010. 应用曲率属性预测裂缝发育带及其产状[J]. 石油地球物理勘探, 45(6): 885-889. |
| [36] | 王世星. 2012. 高精度地震曲率体计算技术与应用[J]. 石油地球物理勘探, 47(6): 965-972. |
| [37] | 文武, 文晓涛. 2011. 曲率在复杂地质体检测中的应用[J]. 石油天然气学报, 33(7): 84-87. |
| [38] | 杨威. 2011. 曲率属性分析及其应用[D]. 成都: 成都理工大学. |
| [39] | 杨威, 贺振华, 陈学华. 2011. 结构方位滤波在体曲率属性中的应用[J]. 石油物探, 50(1): 27-32. |
| [40] | 印兴耀, 高京华, 宗兆云. 2014. 基于离心窗倾角扫描的曲率属性提取[J]. 地球物理学报, 57(10): 3411-3421, doi: 10.6038/cjg20141027. |
 2015, Vol. 30
2015, Vol. 30

