在地球物理勘探领域,地震波速度被作为我们要提取的最重要的参数之一,它是地震资料的重要组成部分,也是反映储层岩石性质的关键参数.地震波速度对于地震及地质资料的解释、储层岩性及流体识别等都是非常重要的.岩石物理学在地震弹性参数与储层物性参数之间起到了桥梁作用(Wang,2001; Mavko et al.,2009),因此,通过岩石物理建模来预测岩石速度具有重要意义.
为解决实际工区常规测井中横波信息缺失的现象,很多学者通过岩石物理模型的构建实现了横波速度的求取.Xu和White(1995)考虑了砂岩孔隙和泥岩孔隙的几何形态,给出了适用于常规砂泥岩储层的Xu-White模型;Keys和Xu(2002)引入干岩石近似对Xu-White模型中干岩石模量求取方法进行了改进;白俊雨等(2012)指出在Xu-White模型中采用变化的孔隙纵横比估算出的横波速度远远比采用固定孔隙纵横比估算出的横波速度准确.Lee(2006)将孔隙形状的影响归因于压实效应,通过改进Pride等(2004)提出的计算压实砂岩干岩石模量的公式,给出了基于固结系数的横波速度预测模型;张广智等(2012)在Xu-White模型的基础上给出了基于修正Xu-White模型的碳酸盐岩横波速度估算方法;张佳佳等(2012)通过改进Nur(1992)提出的临界孔隙度和岩石骨架弹性模量之间的关系式,给出了预测横波速度的可变临界孔隙度模型;张广智等(2013)等,给出了基于碳酸盐岩裂缝岩石物理模型的横波速度和各向异性参数预测方法;李宏兵等(2013)基于DEM解析模型提出根据纵波(和横波)速度反演岩石等效孔隙纵横比进行储层孔隙结构评价和横波速度预测的方法;巴晶等(2013)基于Biot-Rayleigh波动方程,实现了对非饱和岩石的多尺度理论建模,预测了不同尺度下波响应与岩性、流体间的定量联系;唐晓明等(2013)对孔隙、裂隙介质弹性波理论进行了实验研究,指出其能够很好地描述岩石在干燥和饱和状态下纵、横波速度随压力的变化等.
随着油气田勘探开发的深入,致密储层横波预测方法的研究开始受到人们重视.Smith等(2009)分析了低孔低渗砂岩储层特征,将KT模型(Berryman,1980; Kuster and Toksöz,1974)应用于低孔低渗储层;Ruiz和Cheng(2010)基于自相容近似模型(Berryman,1980,1995),给出了适用于致密砂岩气储层的SPM模型和SAR模型;Avseth等(2014)通过对沉积岩石特征的研究给出了适用于中低孔隙的岩石物理模型,高孔隙采用CCT模型(Dvorkin and Nur,1996),低孔隙为DEM模型(Berryman,1995),高低孔隙的过渡用HS上限(Hashin and Shtrikman,1963);陈雪莲等(2014)将孔、裂隙介质弹性波传播理论应用于多极子声波测井的井孔声场模拟,重点研究了致密介质中裂隙发育时多极子声波的传播机理以及衰减特征;董宁等(2014),在自洽模型和微分等效介质模型的基础上,引入Berryman三维孔隙形态及Brown-Korringa固体替代技术,建立适用于富有机质泥页岩的新型岩石物理模型等.致密储层由孔隙和基质组成,岩石速度不仅会受到孔隙的影响,而且会受到基质固体颗粒的影响.在固体颗粒几何形状未知的情况下,HS界限和VR界限只能给出基质模量的可能取值范围.本文基于自相容近似构建了S-S模型,通过测井资料约束来控制不同类型孔隙和固体颗粒的含量,实例应用表明该模型可以提高横波预测的精度,验证了该模型的适用性.
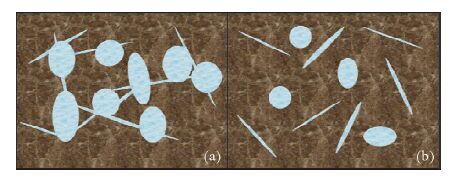
1 致密储层特征致密储层具有不同于常规砂泥岩储层的特征,致密储层包括致密砂岩储层和致密泥页岩储层等.致密砂岩储层一般是指渗透率小于1×10-3μm2,孔隙度小于10%的砂岩储层(戴金星等,2012).致密页岩储层的孔隙度和渗透率则更小,以美国为例,美国主要页岩气盆地的孔隙度一般在2%~14%,集中分布于4.22%~6.51%,渗透率小于0.1×10-3μm2(蒋裕强等,2010).常规砂泥岩储层和低孔低渗储层可等效为图 1(a)和图 1(b)所示模型,图中淡蓝色区域表示岩石的孔隙结构,分为孔隙纵横比较大的孔隙和孔隙纵横比较小的裂隙.其中(a)为常规砂泥岩储层对应的孔隙特征,表现为高孔隙度,高连通性;(b)为低孔低渗储层对应的孔隙特征,表现为低孔隙度,低连通性,甚至不连通.本文致密储层岩石物理建模基于自相容近似模型,自相容近似将岩石孔隙考虑为彼此隔离,流体不能相互流动(Mavko et al.,2009),因此,自相容近似可以用来模拟致密储层低孔低渗特征,这里所考虑的致密储层均不涉及各向异性特征,只是针对岩石的低孔低渗特点开展的研究.
|
图 1 (a)高孔高渗储层(b)低孔低渗储层 Fig. 1 (a)Reservoir with high porosity and high permeability (b)Reservoir with low porosity and low permeability |
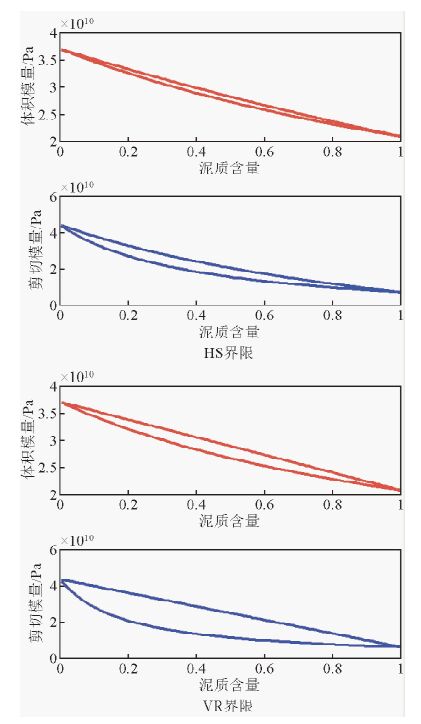
用理论方法来预测矿物颗粒和孔隙混合物的等效弹性模量,需要知道各构成成分的体积含量、各构成成分的弹性模量和各构成成分相互组合在一起的几何细节(Mavko et al.,2009).构建模型求取饱和岩石弹性模量时,基质弹性模量的求取往往不考虑其几何细节.已知基质各个矿物的体积含量和各分量的模量,我们可以利用Hashin-Shtrikman界限或者Voigt-Reuss界限来估算基质弹性模量的取值范围,利用表 1数据,我们能得到图 2所示基质模量的上下限,其中HS界限求取的基质模量范围较小,在VRH均值(Hill et al.,1952)附近波动不大,给出了基质模量最窄的可容许上下界限,VR界限给出了基质模量可能取值的最大范围.为了方便使用,在基质固体颗粒形状不清楚的情况下,通常取HS上下限的平均值或VR上下限的平均值近似求取岩石基质的弹性模量.
|
|
表 1 模型参数 Table 1 Model parameters |
|
图 2 基质模量取值范围 Fig. 2 Matrix modulus value range |
图 2可以看出,在不考虑基质颗粒几何细节的情况下,HS界限和VR界限只能给出基质模量可能的取值范围,基质模量精细求取时需要考虑固体颗粒形状影响.岩石基质由不同的矿物组成,其固体颗粒形状存在差异,如石英和黄铁矿等矿物颗粒的颗粒纵横比较大,颗粒形状近似为圆球状,而黏土和干酪根等矿物颗粒的颗粒纵横比较小,颗粒形状近似为薄片状(Ruiz and Azizov,2011).
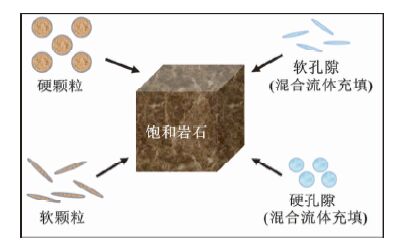
致密储层岩石由孔隙和固体基质组成,岩石模量不仅会受到孔隙几何形状的影响,也会受到基质固体颗粒几何形状的影响.为了考虑孔隙的影响,许多学者将孔隙分为硬孔隙和软孔隙(Smith et al.,2009;Ruiz and Cheng,2010;Avseth et al.,2014),即将岩石孔隙分为孔隙纵横比接近1的硬孔隙和孔隙纵横比为0.01的近似可以描述裂隙的软孔隙,这种组合可以很好的反映致密储层的孔隙特征.另外为了分析基质固体颗粒的影响,我们将颗粒分为硬颗粒和软颗粒,这里的硬颗粒和软颗粒,我们分别定义为纵横比较大,近似为球状和纵横比较小,近似为盘状的基质固体颗粒.同时考虑固体颗粒形状和孔隙形状的影响,饱和岩石被等效为四部分组成,如图 3所示.
|
图 3 等效饱和岩石组分 Fig. 3 Equivalent saturated rock constituents |
为了分析固体颗粒形状和孔隙形状对致密储层速度的影响,我们采用自相容近似建立岩石物理模型.自相容近似模型包含物之间的弹性互动是通过用暂时尚未知的等效基质替换背景介质的方法来近似,可以同时考虑固体颗粒形状和孔隙形状的影响.
我们使用Berryman(1980,1995)给出N相混合物的自相容近似的一般形式.SC模型(即:自相容近似模型)需要通 过迭代求解来解决公式的耦合,如果n+1次迭代得到的饱和岩石体积模量KSC*(n+1)、剪切模量μSC*(n+1)与n次迭代得到的体积模量KSC*(n)、剪切模量μSC*(n)差值满足误差要求,停止迭代,公式为
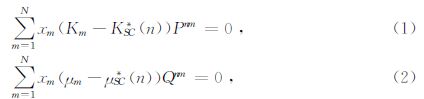
硬孔隙和硬颗粒的包含物系数采用的是Berryman(1995)给出的球体包含物形状的P和Q系数,公式为
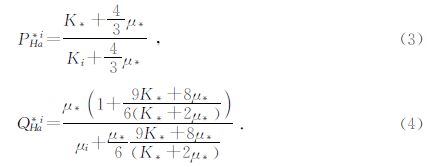
软颗粒包含物系数为盘状包含物形状的P和Q系数,公式为
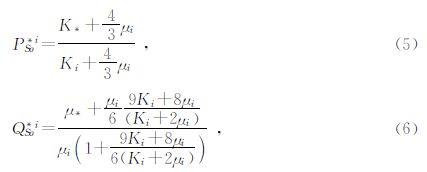
软孔隙的包含物参数我们采用Berryman(1980)给出的任意纵横比椭球状包含物的几何系数P和Q值,软孔隙的孔隙纵横比我们取0.01.
基于SC模型,利用表 1输入参数,我们分析了致密储层颗粒形状和孔隙形状对岩石纵横波速度的影响.为满足致密储层低孔低渗特点,孔隙度取值小于0.12.软孔隙在总孔隙中的含量用a1表示,软颗粒在固体基质中的含量用a2表示.
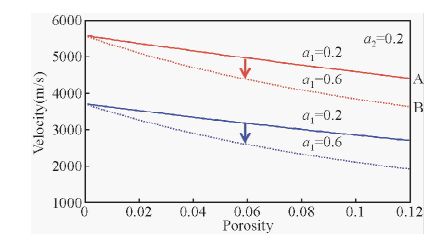
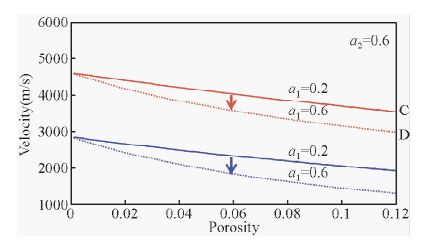
将软颗粒含量a2固定,分析软孔隙含量a1对岩石速度的影响,如图 4和图 5所示.当软颗粒含量a2固定不变时,孔隙度减小会减弱软孔隙含量a1对岩石纵横波速度的影响.增加软颗粒含量a2,软孔隙含量a1对岩石纵横波速度的影响亦会削弱,即速度变化值CD小于AB.
|
图 4 软颗粒含量a2为0.2时,软孔隙含量对岩石速度的影响
(红色曲线为纵波速度,蓝色曲线为横波速度) Fig. 4 The influence of soft pores for velocities of rocks,with soft solid grain content a2 equaling to 0.2 (Red lines are P-wave velocities,blue lines are S-wave velocities) |
|
图 5 软颗粒含量a2为0.6时,软孔隙含量对岩石速度的影响
(红色曲线为纵波速度,蓝色曲线为横波速度) Fig. 5 The influence of soft pores for velocities of rocks, with soft solid grain content a2 equaling to 0.6 (Red lines are P-wave velocities,blue lines are S-wave velocities) |
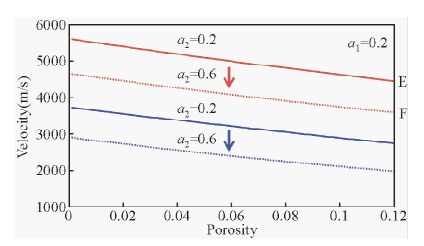
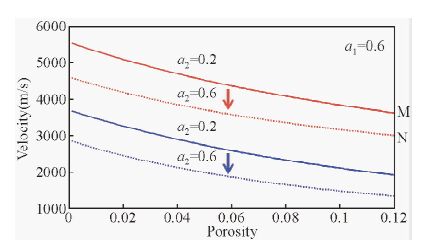
将软孔隙含量a1固定,如图 6和图 7所示,分析软颗粒含量a2变化对岩石纵横波速度的影响.可以看出,软孔隙含量a1固定不变,增大软颗粒含量a2,岩石纵横波速度均会减小.另外,如果增大软孔隙含量a1,软颗粒含量a2对岩石纵横波速度的影响会减弱,即速度变化MN小于EF.
|
图 6 软孔隙含量a1为0.2时,软颗粒含量对岩石速度的影响
(红色曲线为纵波速度,蓝色曲线为横波速度) Fig. 6 The influence of soft solid grains for velocities of rocks, with soft pore content a1 equaling to 0.2 (Red lines are P-wave velocities,blue lines are S-wave velocities) |
|
图 7 软孔隙含量a1为0.6时,软颗粒含量对岩石速度的影响
(红色曲线为纵波速度,蓝色曲线为横波速度) Fig. 7 The influence of soft solid grains for velocities of rocks,with soft pore content a1 equaling to 0.6 (Red lines are P-wave velocities,blue lines are S-wave velocities) |
由以上分析可以得到,岩石纵横波速度受孔隙形状和颗粒形状的共同作用,且两者相互作用,相互影响.另外可以发现,孔隙度较少时,孔隙形状的影响在减弱,基质颗粒形状的影响有所增大.我们将上述考虑软孔隙含量和软颗粒含量变化影响的模型称为S-S模型(soft solid grain and soft pore model).
3 实例应用实例应用为某工区一低孔低渗砂泥岩井,所取井段有效孔隙度在0.1以内.利用井资料中没有孔隙或者孔隙含量非常小的井段或测井点提取固体基质等效矿物模量,如表 2.
|
|
表 2 矿物模量 Table 2 Mineral modulus |
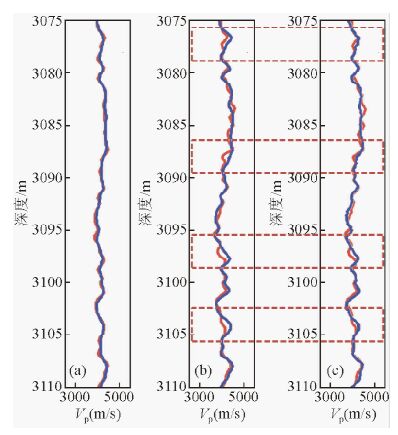
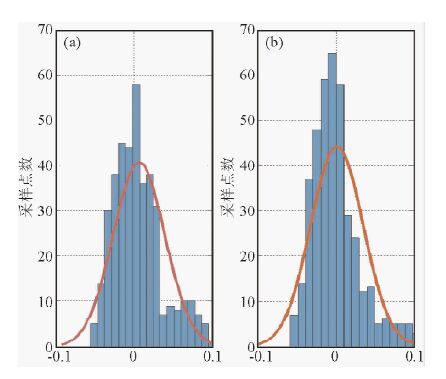
我们将S-S模型与只考虑孔隙形状影响的SC模型进行了比较,横波预测结果如图 8所示,图中(a)为测井纵波和计算纵波,(b)为测井横波和仅考虑孔隙形状影响的SC模型计算横波,(c)为测井横波和S-S模型计算横波.可以看出,S-S模型在保持原有精度基本不变的情况下,部分深度段有所改善,如图 8中红色虚线部分.为了对该模型改进有个整体的认识,我们做了图 9相对误差分布,相对于只考虑孔隙形状影响的SC模型,S-S模型整体得到改善.
|
图 8 横波估算结果比较 (红色曲线为测井纵横波速度,蓝色曲线为计算纵横波速度,其中(b)为SC模型仅考虑孔隙形状影响计算横波,(c)为S-S模型计算横波) Fig. 8 Comparison of shear wave estimation results (Red lines are well log data,blue lines are calculating data,and (b) is the shear wave velocity from SC model only taking the shape of pores into consideration,(c)is the shear wave velocity from S-S model) |
|
图 9 相对误差分布 (a)为SC模型仅考虑孔隙形状影响计算横波相对误差分布;(b)为S-S模型计算横波相对误差分布. Fig. 9 The relative error distribution (a)is the relative error distribution from SC model only taking the shape of pores into consideration;(b)is the relative error distribution from S-S model. |
4.1 随着油气田勘探开发的深入,致密储层的研究越来越受到人们重视,不同于常规砂泥岩储层,致密储层具有低孔低渗的特征.本文利用自相容近似模型来近似模拟致密储层的孔隙特征.不考虑基质固体颗粒的几何细节,HS界限和VR界限只能给出基质模量的大致范围.基质固体颗粒的几何形状是有差异的,它们影响着岩石模量和速度,要提高岩石纵横波速度的求取精度,需要考虑基质颗粒几何形状的影响.
4.2 基于自相容近似,本文给出了一个新的模型S-S模型,该模型同时考虑了孔隙形状(软孔隙和硬孔隙)和固体颗粒形状(软颗粒和硬颗粒)的影响,通过对模型分析,发现固体颗粒形状对岩石纵横波速度有影响,孔隙形状和颗粒形状二者相互作用,相互影响.另外,孔隙度减小时,孔隙形状的影响会减弱,固体颗粒的影响会有所增大.实例应用表明,考虑基质固体颗粒形状的影响,岩石横波速度预测精度得到提高,验证了该模型的有效性和适用性.
致 谢 感谢国家973项目(2013CB228604)对本项研究的资助.同时非常感谢中国石油大学(华东)储层地球物理实验室给过我帮助的各位兄弟姐妹和亲爱的老师们.
| [1] | Avseth P, Johansen T A, Bakhorji A, et al. 2014. Rock-physics modeling guided by depositional and burial history in low-to-intermediate-porosity sandstones[J]. Geophysics, 79(2): D115-D121, doi: 10.1190/geo2013-0226.1. |
| [2] | Ba J, Yan X F, Chen Z Y, et al. 2013. Rock physics model and gas saturation inversion for heterogeneous gas reservoirs[J]. Chinese Journal of Geophysics (in Chinese), 56(5): 1696-1706, doi: 10.6038/cjg20130527. |
| [3] | Bai J Y, Song Z X, Su L, et al. 2012. Error analysis of shear-velocity prediction by the Xu-White model[J]. Chinese Journal of Geophysics (in Chinese), 55(2): 589-595, doi: 10.6038/j.issn.0001-5733.2012.02.021. |
| [4] | Berryman J G. 1980. Long-wavelength propagation in composite elastic media I. Spherical inclusions [J]. The Journal of the Acoustical Society of America, 68: 1809-1831, doi: 10.1121/1.385172. |
| [5] | Berryman J G. 1992. Single-scattering approximations for coefficients in Biot’s equations of poroelasticity[J]. The Journal of the Acoustical Society of America, 91(2): 551-571, doi: 10.1121/1.402518. |
| [6] | Berryman J G. 1995. Mixture theories for rock properties[M].// Rock Physics & Phase Relations: A Handbook of Physical Constants. AGU, 205-228, doi: 10.1029/RF003p0205. |
| [7] | Chen X L, Tang X M, Qian Y P. 2014. Propagation characteristics of multipole acoustic logging in cracked porous tight formations[J]. Chinese Journal of Geophysics (in Chinese), 57(9): 2961-2970, doi: 10.6038/cjg20140921. |
| [8] | Dai J X, Ni Y Y, Wu X Q. 2012. Tight gas in China and its significance in exploration and exploitation[J]. Petroleum Exploration and Development (in Chinese), 39(3): 257-264, doi: 10.1016/S1876-3804(12)60043-3. |
| [9] | Dong N, Huo Z Z, Sun Z D, et al. 2014. An investigation of a new rock physics model for shale[J]. Chinese Journal of Geophysics (in Chinese), 57(6): 1990-1998, doi: 10.6038/cjg20140629. |
| [10] | Dvorkin J, Nur A. 1996. Elasticity of high-porosity sandstones: Theory for two North Sea data sets[J]. Geophysics, 61(5): 1363-1370, doi: 10.1190/1.1444059. |
| [11] | Hashin Z, Shtrikman S. 1963. A variational approach to the theory of the elastic behaviour of multiphase materials[J]. Journal of the Mechanics and Physics of Solids, 11(2): 127-140, doi: 10.1016/0022-5096(63)90060-7. |
| [12] | Hill R. 1952. The elastic behaviour of a crystalline aggregate[J]. Proceedings of the Physical Society. Section A, 65(5): 349-354, doi: 10.1088/0370-1298/65/5/307. |
| [13] | Jiang Y Q, Dong Z D, Qi L, et al. 2010. Basic features and evaluation of shale gas reservoirs[J]. Natural Gas Industry (in Chinese), 30(10): 7-12. |
| [14] | Keys R G, Xu S Y. 2002. An approximation for the Xu-White velocity model[J]. Geophysics, 67(5): 1406-1414, doi: 10.1190/1.1512786. |
| [15] | Kuster G T, Toksöz M N. 1974. Velocity and attenuation of seismic waves in two-phase media: Part I. theoretical formulations [J]. Geophysics, 39(5): 587-608, doi: 10.1190/1.1440450. |
| [16] | Lee M W. 2006. A simple method of predicting S-wave velocity[J]. Geophysics, 71(6): F161-F164, doi: 10.1190/1.2357833. |
| [17] | Li H B, Zhang J J, Yao F C. 2013. Inversion of effective pore aspect ratios for porous rocks and its applications[J]. Chinese Journal of Geophysics (in Chinese), 56(2): 608-615, doi: 10.6038/cjg20130224. |
| [18] | Mavko G, Mukerji T, Dvorkin J. 2009. The Rock Physics Handbook: Tools for Seismic Analysis of Porous Media[M]. Cambridge: Cambridge University Press. |
| [19] | Ruiz F, Cheng A. 2010. A rock physics model for tight gas sand[J]. The Leading Edge, 29(12): 1484-1489, doi: 10.1190/1.3525364. |
| [20] | Ruiz F, Azizov I. 2011. Fluid substitution in tight shale using the soft-porosity model[C]//2011 SEG Annual Meeting. Society of Exploration Geophysicists. 2272-2276. |
| [21] | Smith T M, Sayers C M, Sondergeld C H. 2009. Rock properties in low-porosity/low-permeability sandstones[J]. The Leading Edge, 28(1): 48-59, doi: 10.1190/1.3064146. |
| [22] | Tang X M, Qian Y P, Chen X L. 2013. Laboratory study of elastic wave theory for a cracked porous medium using ultrasonic velocity data of rock samples[J]. Chinese Journal of Geophysics (in Chinese), 56(12): 4226-4233, doi: 10.6038/cjg20131225. |
| [23] | Wang Z J. 2001. Fundamentals of seismic rock physics[J]. Geophysics, 66(2): 398-412, doi: 10.1190/1.1444931. |
| [24] | Xu S Y, White R E. 1995. A new velocity model for clay-sand mixtu res[J]. Geophysical Prospecting, 43(1): 91-118, doi: 10.1111/j.1365-2478.1995.tb00126.x. |
| [25] | Zhang G Z, Chen H Z, Wang Q, et al. 2013. Estimation of S-wave velocity and anisotropic parameters using fractured carbonate rock physics model[J]. Chinese Journal of Geophysics (in Chinese), 56(5): 1707-1715, doi: 10.6038/cjg20130528. |
| [26] | Zhang G Z, Li C C, Yin X Y, et al. 2012. A shear velocity estimation method for carbonate rocks based on the improved Xu-White model[J]. Oil Geophysical Prospecting (in Chinese), 47(5): 717-722. |
| [27] | Zhang J J, Li H B, Yao F C. 2012. Rock critical porosity inversion and S-wave velocity prediction[J]. Applied Geophysics, 9(1): 57-64, doi: 10.1007/s11770-012-0314-8. |
| [28] | 巴晶, 晏信飞, 陈志勇,等. 2013. 非均质天然气藏的岩石物理模型及含气饱和度反演[J]. 地球物理学报, 56(5): 1696-1706, doi: 10.6038/cjg20130527. |
| [29] | 白俊雨, 宋志翔, 苏凌,等. 2012. 基于Xu-White模型横波速度预测的误差分析[J]. 地球物理学报, 55(2): 589-595, doi: 10.6038/j.issn.0001-5733.2012.02.021. |
| [30] | 陈雪莲, 唐晓明, 钱玉萍. 2014. 含孔隙、裂隙致密介质中多极子声波的传播特征[J]. 地球物理学报, 57(9): 2961-2970, doi: 10.6038/cjg20140921. |
| [31] | 戴金星, 倪云燕, 吴小奇. 2012. 中国致密砂岩气及在勘探开发上的重要意义[J]. 石油勘探与开发, 39(3): 257-264, doi: 10.1016/S1876-3804(12)60043-3. |
| [32] | 董宁, 霍志周, 孙赞东,等. 2014. 泥页岩岩石物理建模研究[J]. 地球物理学报, 57(6): 1990-1998, doi: 10.6038/cjg20140629. |
| [33] | 李宏兵, 张佳佳, 姚逢昌. 2013. 岩石的等效孔隙纵横比反演及其应用[J]. 地球物理学报, 56(2): 608-615, doi: 10.6038/cjg20130224. |
| [34] | 唐晓明, 钱玉萍, 陈雪莲. 2013. 孔隙, 裂隙介质弹性波理论的实验研究[J]. 地球物理学报, 56(12): 4226-4233, doi: 10.6038/cjg20131225. |
| [35] | 蒋裕强, 董大忠, 漆麟,等. 2010. 页岩气储层的基本特征及其评价[J]. 天然气工业, 30(10): 7-12. |
| [36] | 张广智, 陈怀震, 王琪,等. 2013. 基于碳酸盐岩裂缝岩石物理模型的横波速度和各向异性参数预测[J]. 地球物理学报, 56(5): 1707-1715, doi: 10.6038/cjg20130528. |
| [37] | 张广智, 李呈呈, 印兴耀,等. 2012. 基于修正Xu-White模型的碳酸盐岩横波速度估算方法[J]. 石油地球物理勘探, 47(5): 717-722. |
 2015, Vol. 30
2015, Vol. 30

