随着偏移技术的发展,地震勘探对于速度模型的要求也越来越高.全波形反演作为一种高精度的速度建模工具,也越来越成为国内外学者研究的热点(范会吉等,1997;丁继才等,2007;卞爱飞等,2010;廖建平等,2011;刘国峰等,2012;王西文等,2013;陈永芮等,2013,董良国等,2013; 杨午阳等,2013;Virieux and Operto,2009).在20世纪80年代Lailly和Tarantola就FWI进行了系统的公式推导,形成了一套比较完整的理论体系(Lailly,1983;Tarantola,1984).在九十年代Pratt将其发展到频率域(Pratt,1999).近些年来,Shin、Cha在Laplace域,Laplace-Fourier混合域也取得了突破性的进展(Shin and Cha,2008,2009;Cha and Shin,2009).
全波形反演通过最小化观测炮记录和合成炮记录之间的误差泛函来更新地下的介质参数,在其每次迭代过程中都会利用所有类型的波,包括回折波、超临界反射波以及多次波.全波形反演由于误差泛函的非线性,反演结果容易落入局部极小值,为了提高反演结果的精度可以在全波形反演的基础上采用多尺度的反演策略.多尺度全波形反演具有高精度、高信噪比、速度恢复准确等优点.但是作为一种迭代寻优的方法,在迭代过程中进行大量的地震数据模拟,巨大的计算量一直是制约多尺度FWI发展的重要因素.为了解决这个问题,Denis将偏移和波形反演结合,迭代中采用成像条件和波形拟合双重标准,提高了速度估计的效率(Trezeguet et al.,1989).Hu基于层状介质的假设在波数域计算了Hessian矩阵的逆,加快了收敛的速度(Hu et al.,2011).除了上述方法外,还可以采用震源编码的方法.这种方法是将多炮的数据合成几个超道集,使得炮的数量减少,从而减少了计算量.Romero、Schuster、Ben-Hadj-Ali、Dai等采用随机相位编码编码技术,将其运用到偏移以及波形反演中,在确保反演精度的同时提高了计算效率(Romero et al.,2000;Schuster et al.,2011;Ben-Hadj-Ali et al.,2011;Dai et al.,2012).但是随机相位编码通常要固定检波器的位置,因此它并不适用于海上数据.为了解决这个问题可以采用同时适用于陆上和海上数据的平面波编码技术.Whitmore、Zhang 、Liu、Stoffa、Li、Hu等将炮域的数据转化为平面波域的数据并选择有限的射线参数进行正演模拟和反演,取得了较好的效果(Whitmore,1995;Zhang et al.,2005;Liu et al.,2006;Stoffa et al.,2006;Li et al.,2014;Hu et al.,2014).同时他们也指出了当炮间距比较大时有比较强的串扰噪声,但是通过不同编码函数的叠加可以削弱这种噪声,且反演迭代的次数越多串扰噪声越弱.
本文将平面波编码运用到时间域多尺度全波形反演中,推导了串扰噪声在时间域产生的原因,给出了时间域平面波全波形反演的具体流程,讨论了单参数与多参数反演的区别以及随机噪声对反演结果的影响,对比了时间域平面波全波形反演与常规全波形反演的效率以及效果,验证了方法的可行性与优越性.
1 方法原理 1.1 时间域多尺度全波形反演全波形反演通过匹配初始模型正演得到的炮记录Pcal(s,x,t)与观测炮记录Pobs(s,x,t)来更新速度模型v(x).这里定义最小二乘误差泛函为
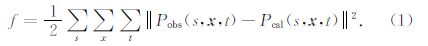
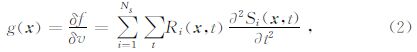
全波形反演的结果容易落入局部极小值,导致反演精度降低.为了解决这个问题,本文采用了Bunks提出的多尺度反演方法(Bunks et al.,1995).该方法通过低通滤波器对数据进行不同频带的滤波,滤波后先利用低频带的数据反演速度场的大构造,并将得到的结果作为高频带的反演输入,再利用高频带数据反演精细构造.多尺度法无论是对时间域还是频率域的FWI都是一个非常简单且行之有效的反演策略.
1.2 平面波多尺度全波形反演虽然时间域全波形反演有着较高的精度,但是巨大的计算量一直制约着它的发展.为了提高计算效率,可以通过混叠震源技术对炮记录进行简单的叠加,将多个炮集的信息融入到一个超道集中.初始速度模型正演模拟得到的波场与反传的残差波场可分别定义为
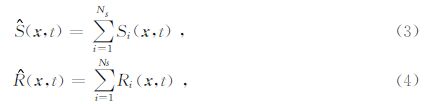
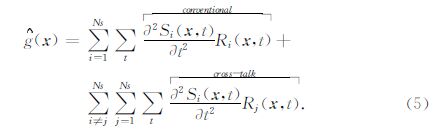
从公式5中可以发现混叠震源产生的梯度可以分为两部分,一部分是常规FWI的梯度,另外一部分是混叠震源产生的串扰噪声.如果不对串扰噪声加以消除,那么反演结果的信噪比将会受到很严重的影响.
为了削弱混叠震源产生的串扰噪声,本文采用线性时移 函数对炮记录进行平面波编码,时移量的大小与震源位置、 震源入射角、以及地表速度有关.其过程可以由公式(6)表示为
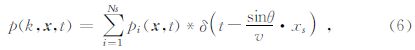
编码后的最小二乘误差泛函变为
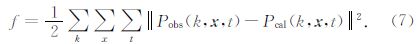
将公式7与公式1进行对比,可以发现两种误差泛函非常类似,只是将炮循环换成了射线参数循环.显然射线参数用的越多,压制串扰噪声的效果越好,但是效率会降低.当射线参数的个数与原始炮数相同时,平面波FWI与常规FWI的效率相同.
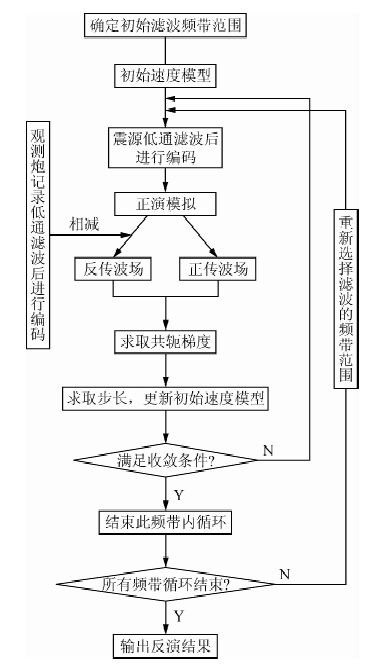
本文所提出的平面波多尺度FWI的反演流程如图 1所示.其具体的实现过程可以概述如下(1)对震源和观测炮记录进行滤波和编码(2)正演模拟后将得到的炮记录与观测炮记录求残差.(3)在每个时刻,反传炮记录残差得到反传波场,并与初始速度模型正演得到的波场做互相关,各个时刻互相关的值叠加后得到梯度.(4)求取步长并更新初始速度模型,经过多次迭代后得到较为准确的反演结果.
|
图 1 平面波FWI流程图 Fig. 1 Flowcharts of plane-wave full waveform inversion |
Marmousi模型作为标准复杂速度模型,可以验证算法在复杂介质条件下的可行性.为了提升计算效率,在保证模型复杂性的同时,对原有模型进行抽稀.修改过后的真实速度模型如图 2a所示,模型的大小为383×120,横向与纵向的网格间距均为10 m.初始速度模型由SU对真实速度模型平滑得到,横向与纵向的平滑因子均为20,平滑后的速度模型如图 2b所示.

|
图 2 (a)真实速度模型,(b)初始速度模型,速度色标单位是m/s Fig. 2 (a)The true velocity model,(b)The smooth velocity model. The color bar has units of m/s. |
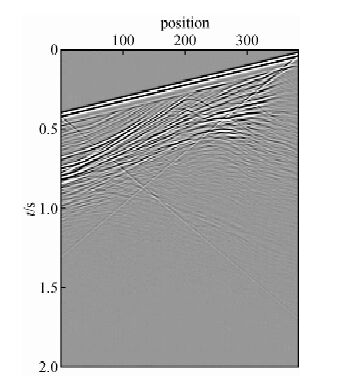
本文采用时间2阶,空间8阶的有限差分法进行正演模拟,选取主频为20 Hz的Ricker子波作为震源.炮点个数为383,每炮都对应383道接收,炮间距与检波点间距为10 m,记录长度为2 s,采样间隔0.5 ms.将正演得到的炮记录进行平面波编码,编码后射线参数k=-0.2 ms/m时的炮记录如图 3所示.
|
图 3 k=-0.2 ms/m时平面波编码后得到的炮记录 Fig. 3 A plane-wave gather with k=-0.2 ms/m |
本文所有的波形反演测试都选择了0~7 Hz、0~14 Hz、0~21 Hz这三个频带,并在每个频带内都迭代40次.图 4a~4c是仅选取射线参数k=0时的反演结果,从浅层到深层有很多像圆圈所标记的串扰噪声,这些噪声严重的影响了反演结果的信噪比.除此以外深层的更新量很少,反演效果较差.
通过适当增加射线参数的个数可以有效的削弱串扰噪声,提高反演结果的质量.图 4d~4f是每次迭代时射线参数从k=-0.2 ms/m到k=0.2 ms/m均匀采样,选取21个参数的反演结果.当频带范围较低时得到的反射界面信息不明显,只有大概的轮廓.随着频带范围的增加,高频成分变多,界面更加清晰,深部的结构也逐渐显现.最终的反演结果与单参数相比,串扰噪声基本消除,深部结构得到了更好的恢复.
对于平面波FWI来说,选择多少个射线参数是决定反演效率与反演质量的关键.个数太多会导致效率降低,而个数太少则不能很好地压制串扰噪声,模型结构的反演效果也会受到影响.根据多次测试的经验,选取20到30个射线参数可以在保持反演效率与质量的同时压制串扰噪声,提高反演结果的信噪比.
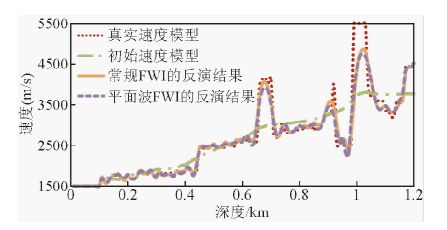
2.4 平面波FWI与常规FWI的效率以及效果对比为了对比两种反演方法的反演效果,本文基于相同的Marmousi模型进行了常规FWI的反演测试,炮点个数为30,反演结果如图 5所示.抽取图 5与图 4.f在CDP=100处的速度,得到的速度曲线如图 6所示.通过对比速度曲线可以发现:两种方法的反演结果基本相同,浅层的速度恢复很理想,跟真实速度接近,深层除了某些速度变化比较剧烈的特殊位置,整体的反演结果还是比较好的.因为两种方法的迭代次数相同,那么效率的比值就是炮点数与射线参数个数的比值.在Marmousi模型的测试中,炮点数和射线参数的个数分别是30和21,因此平面波FWI的计算效率是常规FWI的30/21≈1.5倍.在相同反演效果的情况下,平面波FWI极大的提高了计算效率.

|
图 4 (a)仅有一个射线参数的反演结果(0~7 Hz),(b)仅有一个射线参数的反演结果(0~14 Hz),(c)仅有一个射线参数的反演结果(0~21 Hz),(d)21个射线参数的反演结果(0~7 Hz),(e)21个射线参数的反演结果(0~14 Hz),(f)21个射线参数的反演结果(0~21 Hz),速度色标单位是m/s Fig. 4 (a)The inversion result with only one ray parameter(0~7 Hz),(b)The inversion result with only one ray parameter(0~14 Hz),(c)The inversion result with only one ray parameter(0~21 Hz),(d)The inversion result with 21 ray parameters(0~7 Hz),(e)The inversion result with 21 ray parameters(0~14 Hz), (f)The inversion result with 21 ray parameters(0~21 Hz).The color bar has units of m/s |

|
图 5 常规FWI反演结果,速度色标单位是m/s Fig. 5 The inversion result of conventional FWI. The color bar has units of m/s |
|
图 6 CDP=100时的速度曲线 Fig. 6 The velocity curve(CDP=100) |
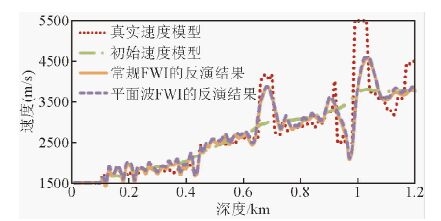
为了验证两种方法的抗噪性,对观测炮记录加入S/N等于1的高斯随机噪声后进行反演,反演结果见图 7.图 8是真实速度模型、初始速度模型、常规反演结果与平面波反演结果在CDP=100处的速度对比曲线.常规FWI与平面波FWI在加入相同噪声的情况下反演结果非常接近,1.1 km以上的中浅层的反演效果比较理想.这说明两种方法都具有一定的抗噪性,并且抗噪声能力基本相同.表 1列出了常规FWI与平面波FWI在各个方面的对比.

|
图 7 (a)常规FWI反演结果(S/N=1),(b)平面波 FWI的反演结果(S/N=1),速度色标单位是m/s Fig. 7 (a)The inversion result of conventional FWI (S/N=1),(b)The inversion result of plane-wave FWI(S/N=1). The color bar has units of m/s. |
|
图 8 CDP=100时的速度曲线 Fig. 8 The velocity curve(CDP=100) |
|
|
表 1 Marmousi模型中常规FWI与基于平面波编码的FWI的对比 Table 1 Comparison of different parameters for conventional FWI and plane-wave FWI in Marmousi model. |
为了改善全波形反演的运算效率,本文实现了基于平面波编码的时间域多尺度全波形反演.在实现方法的基础上对Marmousi模型进行了测试,得到了以下几点认识:
(1)射线参数越多,压制串扰噪声的效果越好.但是如果射线参数太多,就不能体现出这种方法的效率优势,串扰噪声的改善也非常有限.
(2)平面波FWI具有一定的抗噪声能力,与常规FWI的抗噪声能力相当.
(3)在相同迭代次数的情况下,平面波FWI与常规FWI的反演效果非常接近,但是显著提升了计算效率.炮点数与射线参数个数相差越多,效率提升越明显.
虽然该方法已经能够很好地压制串扰噪声,提升计算效率,但是随着迭代次数的增加其计算量仍然很大.为此,在随后的研究中,我们采取的措施是:
(1)将引入预条件算子与正则化算子来加快收敛速度(王薇等,2013);
(2)引入去模糊化滤波器,避免为了削弱串扰噪声而选择过多的射线参数而增加的计算量(Dai and Schuster,2009;Dai et al.,2011).
(3)使用双变网格和GPU加速等技术,进一步提高计算效率(Jastram and Behle,1992;张慧和李振春,2011;李振春等,2008).通过以上几种方法的结合可以使FWI更好地运用到实际资料的处理.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!
| [1] | Ben-Hadj-Ali H, Operto S, Virieux J. 2011. An efficient frequency-domain full waveform inversion method using simultaneous encoded sources[J]. Geophysics, 76(4): R109-R124. |
| [2] | BianAF, YuWH, ZhouHW. 2010. Progress in the frequency-domain full waveform inversion method[J]. Progress in Geophysics (in Chinese), 25(3): 982-993, doi: 10.3969/j.issn.1004-2903.2010.03.037. |
| [3] | Bunks C, Saleck F M, Zaleski S, et al. 1995. Multiscale seismic waveform inversion[J]. Geophysics, 60(5): 1457-1473. |
| [4] | Cha Y H, Shin C. 2009. 2D Laplace-Fourier-domain full waveform inversion for both velocity and density models: An experience of the 2004 BP velocity-analysis benchmark dataset[C].//SEG Technical Program Expanded Abstracts. SEG, 2258-2261. |
| [5] | Chen Y R, Li Z C, Qin N, et al. 2013. Full waveform inversion with wave equation bi-directional illumination optimization[J]. Progress in Geophysics (in Chinese), 28(6): 3015-3021, doi: 10.6038/pg20130624. |
| [6] | Dai W, Schuster J. 2009. Least-squares migration of simultaneous sources data with a deblurring filter[C].//SEG Technical Program Expanded Abstracts.SEG,2990-2994. |
| [7] | Dai W, Wang X, Schuster G T. 2011. Least-squares migration of multisource data with a deblurring filter[J]. Geophysics, 76(5): R135-R146. |
| [8] | Dai W, FowlerP, Schuster G T. 2012. Multi-source least-squares reverse time migration[J].Geophysical Prospecting, 60(4): 681-695. |
| [9] | Ding J C, Chang X, Liu Y K, et al. 2007. Layer by layer waveform inversion of seismic reflection data[J]. Chinese Journal of Geophysics (in Chinese), 50(2): 574-580. |
| [10] | Dong L G, Chi B X, Tao J X, et al. 2013. Objective function behavior in acoustic full-waveform inversion[J]. Chinese Journal of Geophysics (in Chinese), 56(10): 3445-3460, doi: 10.6038/cjg20131020. |
| [11] | Fan H J, Shao X Z, Zhang J R. 1997. Waveform inversion method and its application to data recorded at Tian-Shan mountain area[J]. Acta Geophysica Sinica (in Chinese), 40(3): 369-379. |
| [12] | Hu J X, Schuster G T, Valasek PA. 2011. Poststack migration deconvolution[J]. Geophysics, 66(3): 939-952. |
| [13] | Hu JT, Shao Y, WangMX, et al. 2014. An efficient amplitude encoding scheme for reverse time migration[C].//76th EAGE Conference& Exhibition. EAGE. |
| [14] | Jastram C, Behle A. 1992. Acoustic modelling on a grid of vertically varying spacing[J]. Geophys. Prosp., 40(2): 157-169. |
| [15] | Lailly P. 1983. The seismic inverse problem as a sequence of before stack migrations[C].//Conference on Inverse Scattering, Theory and Application, Society for Industrial and Applied Mathematics, Expanded Abstracts.206-220. |
| [16] | Li C, Huang JP, Li ZC, et al. 2014. Application of plane-wave least square migration in fault block reservoirs: a case study[C].//76th EAGE Conference & Exhibition. EAGE. |
| [17] | Li Z C, Zhang H, Zhang H. 2008. Variable-grid high-order finite-difference numeric simulation of first-order elastic wave equation[J]. Oil Geophysical Prospecting (in Chinese), 43(6): 711-716. |
| [18] | LiaoJP, LiuHX, WangHZ, et al. 2011. High resolution acoustic wave full waveform velocity inversion in frequency space domain-theoretical model[J]. Progress in Geophysics (in Chinese), 26(5): 1690-1695, doi:10.3969/j.issn.10042903.2011.05.023. |
| [19] | Liu F Q, Hanson D W, Whitmore N D, et al. 2006. Toward a unified analysis for source plane-wave migration[J]. Geophysics, 71(4): S129-S139. |
| [20] | Liu G F, Liu H, Meng X H, et al. 2012. Frequency-related factors analysis in frequency domain waveform inversion[J]. Chinese Journal of Geophysics (in Chinese), 55(4): 1345-1353, doi: 10.6038/j.issn.0001-5733.2012.04.030. |
| [21] | Moczo P. 1989. Finite-difference technique for SH waves in 2-D mediausing irregular grids: application to the seismic response problem[J]. Geophys. J. Int., 99(2): 321-329. |
| [22] | Pratt R G. 1999. Seismic waveform inversion in the frequency domain, Part 1: Theory and verification in a physical scale model[J]. Geophysics, 64(3): 888-901. |
| [23] | Romero L A, Ghiglia D C, Ober C C, et al. 2000. Phase encoding of shot records in prestack migration[J]. Geophysics, 65(2): 426-436. |
| [24] | Schuster G T, Wang X, Huang Y, et al. 2011. Theory of multisource crosstalk reduction by phase-encoded statics[J].Geophys. J. Int.,184(3): 1289-1303. |
| [25] | Shin C, Cha Y H. 2008. Waveform inversion in the Laplace domain[J]. Geophys. J. Int., 173(3): 922-931. |
| [26] | Shin C, ChaYH. 2009. Waveform inversion in the Laplace-Fourier domain[J]. Geophys. J. Int., 177(3): 1067-1079. |
| [27] | Stoffa P L, Sen M K, Seifoullaev R K, et al. 2006. Plane-wave depth migration[J]. Geophysics, 71(6): S261-S272. |
| [28] | Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysical Prospecting, 49(8): 1259-1266. |
| [29] | Trezeguet D,Vujasinovic Y, TarantolaA. 1989. Velocity model optimization by image focusing and waveform modeling using prestack depth migration[C].//SEG Technical Program Expanded Abstracts.SEG, 1247-1250. |
| [30] | Virieux J, Operto S. 2009. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 74(6): WCC1-WCC26. |
| [31] | WangW, HanB, TangJ P. 2013. Regularization method with sparsity constraints for seismic waveform inversion[J]. Chinese J. Geophys. (in Chinese), 56(1): 289-297, doi: 10.6038/cjg20130130. |
| [32] | WangXW, YangWY, LüB, et al. 2013. Grasp of the world geophysical technology development status, to promote seismic data processing and interpretation of technological progress[J]. Progress in Geophysics (in Chinese), 28(1): 224-239, doi: 10.6038/pg20130124. |
| [33] | Whitmore N. 1995. An imaging hierarchy for common angle plane wave seismograms[Ph. D. thesis].Tulsa:University of Tulsa. |
| [34] | Yang WY, Wang XW, Yong XS, et al. 2013. The review of seismic full waveform inversion method[J]. Progress in Geophysics (in Chinese), 28(2): 766-776, doi: 10.6038/pg20130225. |
| [35] | ZhangH, LiZ C. 2011. Seismic wave simulation method based on dual-variable grid[J]. Chinese Journal of Geophysics (in Chinese), 54(1): 77-86, doi: 10.3969/j.issn.0001-5733.2011.01.009. |
| [36] | Zhang Y, Sun J, Notfors C, et al. 2005. Delayed-shot 3D depth migration[J]. Geophysics, 70(5): E21-E28. |
| [37] | 卞爱飞, 於文辉, 周华伟. 2010. 频率域全波形反演方法研究进展[J]. 地球物理学进展, 25(3): 982-993, doi: 10.3969/j.issn.1004-2903.2010.03.037. |
| [38] | 陈永芮, 李振春, 秦宁,等. 2013. 波动方程双向照明优化的全波形反演[J]. 地球物理学进展, 28(6): 3015-3021, doi: 10.6038/pg20130624. |
| [39] | 丁继才, 常旭, 刘伊克,等. 2007. 反射地震数据的逐层波形反演[J]. 地球物理学报, 50(2): 574-580. |
| [40] | 董良国, 迟本鑫, 陶纪霞,等. 2013. 声波全波形反演目标函数性态[J]. 地球物理学报, 56(10): 3445-3460, doi: 10.6038/cjg20131020. |
| [41] | 范会吉, 邵学钟, 张家茹. 1997. 波形反演方法及其在新疆地区转换波测深中的应用[J]. 地球物理学报, 40(3): 369-379. |
| [42] | 李振春, 张慧, 张华. 2008. 一阶弹性波方程的变网格高阶有限差分数值模拟[J]. 石油地球物理勘探, 43(6): 711-716. |
| [43] | 廖建平, 刘和秀, 王华忠,等. 2011. 高分辨率的频率空间域声波全波形速度反演-理论模型[J]. 地球物理学进展, 26(5): 1690-1695, doi:10.3969/j.issn.10042903.2011.05.023. |
| [44] | 刘国峰, 刘洪, 孟小红,等. 2012. 频率域波形反演中与频率相关的影响因素分析[J]. 地球物理学报, 55(4): 1345-1353, doi: 10.6038/j.issn.0001-5733.2012.04.030. |
| [45] | 王薇, 韩波, 唐锦萍. 2013. 地震波形反演的稀疏约束正则化方法[J]. 地球物理学报, 56(1): 289-297, doi: 10.6038/cjg20130130. |
| [46] | 王西文, 杨午阳, 吕彬,等. 2013. 把握世界物探技术发展现状, 促进地震资料处理、解释技术进步[J]. 地球物理学进展, 28(1): 224-239, doi: 10.6038/pg20130124. |
| [47] | 杨午阳, 王西文, 雍学善,等. 2013. 地震全波形反演方法研究综述[J].地球物理学进展, 28(2): 766-776, doi: 10.6038/pg20130225. |
| [48] | 张慧, 李振春. 2011. 基于双变网格算法的地震波正演模拟[J]. 地球物理学报, 54(1): 77-86, doi: 10.3969/j.issn.0001-5733.2011.01.009. |
 2015, Vol. 30
2015, Vol. 30

