2. 长江大学地球物理与石油资源学院, 武汉 430100;
3. 川庆钻探工程有限公司地球物理勘探公司, 成都 610213
2. Key laboratory of oil and gas resources and exploration, Yangtze University, Wuhan 430100, China;
3. Chuanqing drilling engineering and geophysical exploration company, Chengdu 610213, China
岩石物理学是一门综合性的学科,它将地球物理学、岩石学、岩土力学和工程地质学等多门学科联系到一起,建立了地震信息和储层参数的联系纽带.流体替换是岩石物理的重要组成部分,也是AVO和四维地震勘探的基础,是储层流体识别和定量化研究的重要工具.在流体替换中最常用的理论就是Gassmann等效介质理论.
Gassmann方程由Gassmann(1951)于1951年提出.该方程建立起岩石体积模量、孔隙度、孔隙流体体积模量和岩石骨架体积模量之间的关系.Biot(1956)于1956年发展了Gassmann理论,为双向介质波动理论的奠定了基础.Plona(1980)在实验中观测到第二类纵波,从而证明了Biot理论的正确性.王尚旭(1990)研究了双相介质中地震波的传播规律,并实现了双相介质中地震波传播的有限元解法.Dvorkin和Nur(1993)(Dvorkin et al.,1994)基于全局流动的Biot模型和局部流动的喷射模型,提出了更适应弹性波在孔隙岩石中传播规律的Biot-Squirt(BISQ)模型.陈信平和刘素红(1996)介绍了该方程的导出及应用和限制.杨顶辉等(2000)论述并总结了BISQ模型的应用前景和存在问题.史謌等(2002)通过实验证明在含孔隙饱和岩石中,弹性波的传播速度随有效压力的增大的增加,且在0~100 Hz的低频范围内,Gassmann方程成立,同时传统的Gassmann理论也适用于频率不高于104 Hz的声波测井.周巍和杨红霞(2005)根据Berryman散射模型,结合Gassmann方程和Walsh公式研究表明,由于裂隙的不同,对于具有相同矿物成分和孔隙率的岩石,其物理参数如体积模量、孔隙弹性模量等都有明显不同,且随着孔隙纵横比的增大,流体对岩石物性的影响减小.孙福利等(2008)应用Biot-Gassmann低频速度模型,并结合Pride公式,建立了岩石基质和骨架的弹性模量关系,证明了纵波速度大小与固结系数的关系.张佳佳等(2010)将常见的广泛使用的岩石骨架模型如Krief模型、Nur模型和Pride模型应用于Biot-Gassmann理论中,并进行理论模型正演等速度分析等,分析常见岩石骨架模型的适用范围.宋洪勇等(2010)基于Gassmann方程,模拟不同流体类型和不同孔隙度的碳酸岩生物礁储层的地震响应特征.李燕等(2010)分析了Gassmann模型的原理和适用范围,并提出了基于Gassmann模型正反演相结合的横波速度曲线优化估算方法.张金强等(2010)使用统计平均的方法,结合全波测井资料,应用Gassmann方程求取岩石骨架的弹性参数.针对碳酸盐岩的基质矿物类型非单一且孔隙结构复杂多变的特点,熊晓军等(2012)以常规Gassmann方程为基础,采用流体因子分析实现碳酸盐岩的流体替换.
在实际的数据处理中,由于数据的采集误差或是岩性变化,流体替换所使用的参数往往与真实值存在误差.本文将对Gassmann方程中所涉及的参数进行讨论,并基于Gassmann方程,探讨参数对流体替换的影响权重.首先介绍Gassmann方程的原理,然后分析参数的变化对最终结果的影响范围,对造成的误差结果进行分析.通过对这些参数对结果的影响分析,可以对流体替换起到优化和指导作用.
1 Gassmann方程原理简述在低频条件下,Gassmann方程是与Biot理论是一致的.它描述了岩石弹性模量随孔隙和流体的不同产生的变化结果.其表达式既可由Biot理论推导出,也可由功的互等原理推导出.
根据Gassmann方程,孔隙岩石的理想结构是由骨架和流体组成.岩石的骨架既可以由一种岩石构成,也可以由多种岩石构成.流体既可以是单相流体,也可以是多相流体共存.
Gassmann方程建立在5点假设条件之上:
1 )岩石在宏观上是均质的;2)所有孔隙都是相通的;3)所有孔隙都充满流体;4)研究中的岩石流体系统是封闭的;5)孔隙流体与岩石骨架间无物理或化学作用.假设2和假设3确保了孔隙流体流动的充分均衡,即意味着波的频率为零,构成了Gassmann方程的本质.方程的形式为
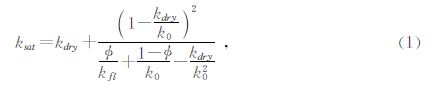
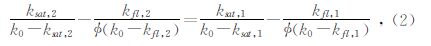
在Gassmann理论中,认为岩石的体积模量会随着流体性质的改变而改变,而岩石的剪切模量是不变的,即:


流体替换的实质是指岩石初始状态下,由纵横波速度、孔隙度、密度等物理参数,来求取岩石在另一饱和流体状态下的岩石物理参数.初始状态可以是干岩石,也可以是饱和岩石.
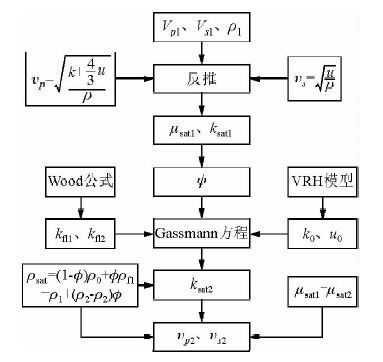
图 1 为基于Gassmann方程的流体替换方法的整个实现流程,首先根据初始状态的纵横波速度和岩石的密度,通过经典的岩石物理学公式(4)(5),反推出岩石的剪切模量和体积模量,然后通过Wood公式和VRH模型求取初始流体和替换流体的体积模量和岩石基质的体积模量,进而结合已知的孔隙度等参数,通过Gassmann方程求取替换后岩石的体积模量,最后确保岩石的剪切模量不变,结合替换后的密度,求取新状态下的纵横波速度.
|
图 1 流体替换流程 Fig. 1 The process of fluid substitution |
Gassmann理论需要输入岩石各构成成分的密度、体积模量、剪切模量和体积比例,流体的组成及各成分的体积模量和密度等参数.岩石模型基本参数见表 1.气饱和岩石的体积模量为12.29 GPa,水饱和岩石的体积模量为17.6 GPa.
|
|
表 1 岩石和流体的物理参数 Table 1 Physical parameters of fluid and rock |
流体替换最常见的两种类型:一是将干岩石替换为含有流体的饱和岩石;二是将从一种流体饱和状态替换到另一种流体饱和状态.毫无疑问,参数的选取对流体替换的整个过程中起着近乎决定的作用.在实际流体替换的过程中,由于存在测量误差,数据本身存在偏差,计算所选取的各个数值实际上与真实值存在着或多或少的差别.分析每个参数对纵横波计算结果的影响,将对整个流体替换过程起到指导和优化作用.下面我们将分情况对参数的影响权重进行分析.
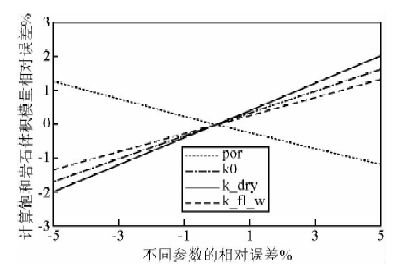
3.1 干岩石替换为饱和岩石在此过程中,干岩石的弹性模量等参数数据通常来源于实验室测量.因此,在模拟将干岩石替换为饱和岩石的过程中,将目标流体状态设置为100%含水,孔隙度设置为0.2,干岩石的体积模量设置为12 GPa.对于输入参数,采用5%的误差范围,使用公式(1)计算饱和岩石的体积模量,参数对结果的影响如图 2所示.
|
图 2 计算误差随模型参数误差的变化 Fig. 2 The changes of calculation error with parameters error |
图 2显示,干岩石体积模量(k_dry)的变化对计算出的饱和岩石体积模量的影响最大,基质弹性模量(k0)次之,孔隙度(por)的影响最小.随着基质弹性模量、流体体积模量(k_fl_w)和干岩石体积模量的增加,计算出的饱和岩石体积模量减小;而孔隙度起的作用相反.
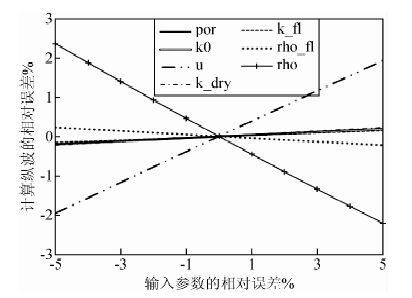
为考察参数误差对流体替换结果——纵横波速度的直接影响,将流体替换中的所有输入参数采用5%的误差范围,分别进行计算.参数误差对纵横波速度的影响见图 3,图 4.
|
图 3 计算纵波速度误差随参数误差的相对变化 Fig. 3 Relative changes of p-wave error with parameter error |
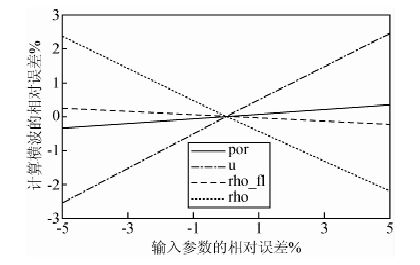
|
图 4 计算横波速度误差随参数误差的相对变化 Fig. 4 Relative changes of s-wave error with parameter error |
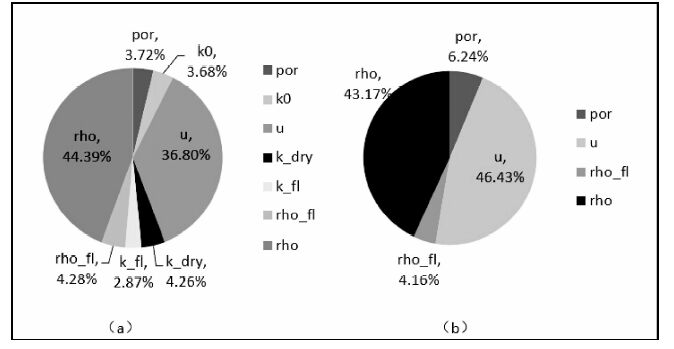
从图 3,图 4中可以看出,随着流体密度和岩石骨架密度的增加,纵横波的速度均减小,其余的输入参数与之作用相反.当输入参数误差为-5%时,对影响纵横波速度的因素进行分析,分别将单个输入参数造成的误差比上所有输入参数造成的误差之和,便可知道此参数相对与其他参数的对于计算最终结果的敏感性.计算纵横波速度误差影响因素的敏感性如图 5所示.从图 5中可见,在由干岩石替换为饱和岩石时,岩石骨架密度和剪切模量对计算结果的影响最大.
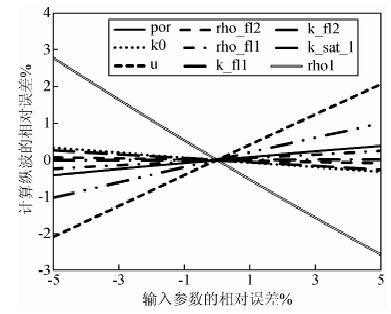
3.2 饱和岩石从一种流体替换为另一种流体流体替换的另一常见类型是从一种饱和流体状态替换到另一种饱和流体状态.如果只知道初始状态的纵横波速度,可以通过公式(4)(5)的变形式计算弹性模量,在依照第二节的流体替换流程进行计算.设置岩石模型从100%含水饱和到100%含气饱和,水饱和岩石的体积模量为17.6 GPa.参数误差对替换后纵横波速度的影响见图 6、图 7.
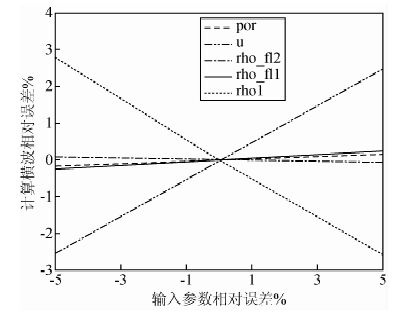
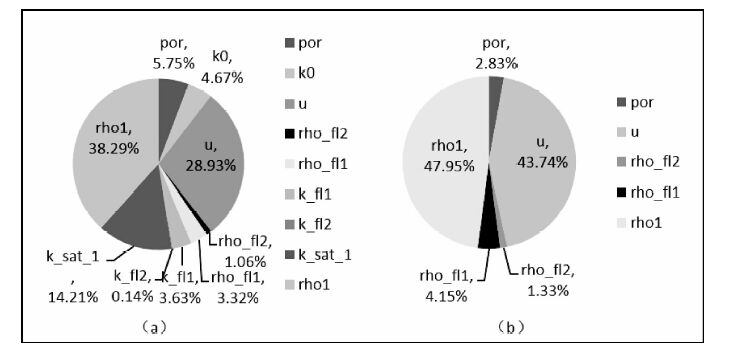
从图 6、图 7中,可以知道,随着初始状态的流体体积模量和岩石密度、岩石基质体积模量和目的状态的流体密度的增加,纵横波速度减小;其他输入参数与之情况相反.当输入参数误差为-5%时,计算纵横波速度误差影响的敏感性如图 8所示.从图 8中可见,在由干岩石替换为饱和岩石时,岩石密度和剪切模量对计算结果的影响最大.
|
图 5 (a)纵波输入参数误差的相对权重;(b)横波输入参数误差的相对权重 Fig. 5 (a)Relative weighting of p-wave input parameter error; (b)Relative weighting of s-wave input parameter error |
|
图 6 计算纵波速度误差随参数误差的相对变化 Fig. 6 Relative changes of p-wave error with parameter error |
|
图 7 计算横波波速度随参数误差的相对变化 Fig. 7 Relative changes of s-wave error with parameter error |
|
图 8 (a)纵波输入参数误差的相对权重;(b)横波输入参数误差的相对权重 Fig. 8 (a)Relative weighting of p-wave input parameter error;(b)Relative weighting of s-wave input parameter error |
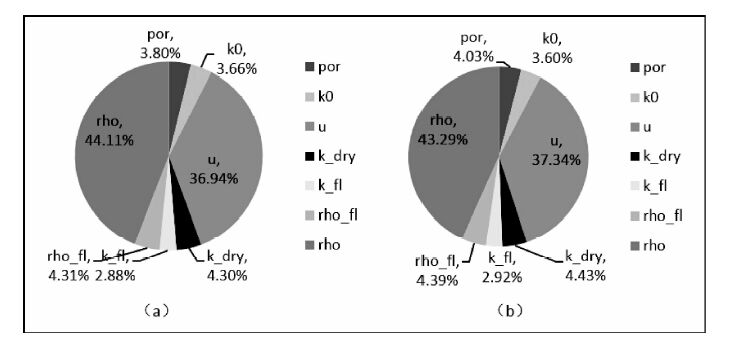
在进行数值模拟时,由于Gassmann理论中所涉及到部分公式不是线性的,所以尽管输入参数是按照线性变化的,且结果计算出的是相对变化值,但是结果的误差相对变化量不是定值,而是按照一定的趋势小幅变化.如再将干岩石替换为饱和岩石的过程中,分别将输入参数的误差设置为-3%和3%,计算每种输入参数相对于其他参数对纵波结果的敏感性,结果如图 9.从图 9中可以看到,在误差从-3%~3%的过程中,剪切模量造成的误差对结果的影响比重从36.94%变化到了37.34%.随着输入参数的增加,纵横波速度的误差变化情况见表 2.
|
图 9 (a)输入参数减少3%纵波的相对变化;(b)输入参数增加3%纵波的相对变化 Fig. 9 (a)Relative changes of input parameter decrease 3%;(b)Relative changes of input parameter increase 3% |
|
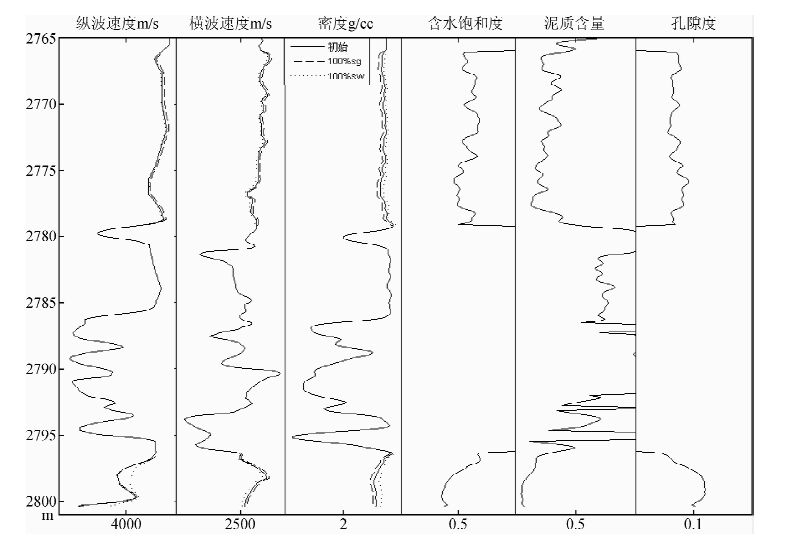
图 10 流体替换实例 Fig. 10 An example of fluid substitution |
基于上文的分析,对某地区的D11井进行流体替换研究.我们分别对岩石的密度和泥质含量进行精细解释:根据分析化验资料,基于岩心密度数据对密度曲线进行校正;采用自然伽马测井信号的维纳滤波等手段,对泥质含量进行修正.将初始流体(气水混合物)分别替换为100%的水和100%的气.替换结果如图 10所示.纵轴为深度,横轴从左到右分别为纵波速度、横波速度、 密度、 含水饱和度、泥质含量和孔隙度.替换后,100%含水时的密度和纵波速度大于100%含气,初始状态居于两者之间.横波速度的情况与之相反.极少部分区段出现100%含气的纵波速度大于100%含水的纵波速度,这是由于模量的变化率小于密度的变化率.在2796~2801 m段,初始状态与100%含水状态下,纵波最大差异为492 m/s,横波最大差异为35 m/s;初始状态与100%含气状态相比,纵波最大差异为90 m/s,横波最大差异为30 m/s.由此可见,横波对流体变化的不敏感,且100%含水时的纵横波速度的变化范围大于100%含气时的变化范围,且纵波的变化比横波剧烈.
|
|
表 2 输入参数的增加与流体替换后纵横波速度相对误差的变化 Table 2 The changes of p-wave and s-wave when input parameter increasing |
本文对基于Gassmann方程流体替换理论,针对最常见的两种流体替换类型,分别计算了各个输入参数对流体替换后纵横波速度的影响,根据计算结果,得到如下结论:
(1)随着岩石的密度与剪切模量的变化,流体替换后的纵横波速度变化明显,即岩石对岩石的密度和剪切模量较为敏感.
(2)孔隙度对结果的影响较小,这主要是因为在求取速度时,孔隙度在求取岩石等效密度和新的饱和岩石体积模量中,起着相反的作用,导致结果中影响比例较小.但在实际地球物理环境中,由于孔隙度影响着流体替换中的多个参数,因此,对孔隙度的选取仍需重视.
(3)由于地质情况的复杂,造成流体替换的实际数据往往存在误差,通过对参数误差对流体替换结果的影响分析,可对数据处理起到指导作用.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!
| [1] | Biot M A. 1956. Theory of propagation of elastic waves in a fluid-saturated porous solid. Part Ⅰ: Low-frequency range[J]. J. Acoust. Soc. Am., 28(2): 168-178, doi: 10.1121/1.1908239. |
| [2] | Chen X P, Liu S H. 1996. An preliminary introduction to Gassmann equation[J]. China Offshore Oil and Gas (Geology) (in Chinese), 10(2): 122-127. |
| [3] | Dvorkin J, Nur A. 1993. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms[J]. Geophysics, 58(4): 524-533. |
| [4] | Dvorkin J, Nolen-Hoeksema R C, Nur A. 1994. The squirt-flow mechanism; macroscopic description[J]. Geophysics, 59(3): 428-438. |
| [5] | Gan L D. 2003. 4D seismic and it’s application to the monitoring of water flooding reservoir (in Chinese)[Ph. D. thesis]. Beijing: China University of Geosciences. |
| [6] | Gassmann F. 1951. Elastic waves through a packing of spheres[J]. Geophysics, 16(4): 673-685. |
| [7] | Hill R. 1963. Elastic properties of reinforced solids: Some theoretical principles[J]. Journal of the Mechanics and Physics of Solids, 11(5): 357-372. |
| [8] | Huang W Q, Hao S B, Wu X Y. 2011. 2011. A method for shear-wave velocity prediction with error correction[J]. Progress in Geophysics (in Chinese), 26(6): 2184-2189, doi: 10.3969/j.issn.1004-2903.2011.06.036. |
| [9] | Li H B, Zhang J J, Yao F C. 2013. Inversion of effective pore aspect ratios for porous rocks and its applications[J]. Chinese J. Geophys. (in Chinese), 56(2): 608-615, doi: 10.6038/cjg20130224. |
| [10] | Li W X, Shi G, Wang H, et al. 2007. The study on the relationships of elastic properties of rock physics[J]. Progress in Geophysics (in Chinese), 22(5): 1380-1385, doi: 10.3969/j.issn.1004-2903.2007.05.007. |
| [11] | Li W X, Wang H, Yao Z X, et al. 2009. Shear-wave velocity estimation and fluid substitution by constraint method[J]. Chinese J. Geophys. (in Chinese), 52(3): 785-791. |
| [12] | Li Y, Liu H J, Wang Y M. 2010. Mechanism analysis of Gassmann model and its application[J]. Progress in Exploration Geophysics (in Chinese), 33(1): 16-20. |
| [13] | Liu L F, Sun Z D, Han J F, et al. 2014. A carbonate fluid identification method based on quantum particle swarm fuzzy neural network[J]. Chinese J. Geophys. (in Chinese), 57(3): 991-1000, doi: 10.6038/cjg20140328. |
| [14] | Plona T J. 1980. Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies[J]. Applied Physics Letters, 36(4): 259-261. |
| [15] | Shi G, Yang D Q. 2002. Determination of the elastic wave velocities in porous rocks with the change of overburden pressure and its universal significance[J]. Science China Earth Sciences, 45(7): 635-642. |
| [16] | Song H Y, Xiong X J, Lin K, Li Y. 2010. Fluid substitution based on carbonate reef reservoir[J]. Journal of Yangtze University (Nat Sci Edit) (in Chinese), 7(1): 47-50. |
| [17] | Sun F L, Yang C C, Ma S H, et al. 2008. An S-wave velocity predicted method[J]. Progress in Geophysics (in Chinese), 23(2): 470-474. |
| [18] | Wang Y C, Du W L, Liu X H, et al. 2014. Inversion of transverse wave velocity with logging data and its effect analysis of application[J]. Progress in Geophysics (in Chinese), 29(4): 1798-1802, doi: 10.6038/pg20140441. |
| [19] | Wu L, Liu T Y, Wang H T, et al. 2014. Comparison of dry rock moduli in different models and their applications[J]. Progress in Geophysics (in Chinese), 29(5): 2272-2277, doi: 10.6038/pg20140542. |
| [20] | Xing X J, Lü Y, Lin K, et al. 2012. A novel method of fluid substitution in carbonates[J]. Journal of China University of Petroleum (in Chinese), 36(6): 57-61, doi: 10.3969/j.issn.1673-5005.2012.06.010. |
| [21] | Yang D H, Zhang Z J, Teng J W, et al. 2000. The study of two-phase anisotropy questions and applied prospects[J]. Progress in Geophysics (in Chinese), 15(2): 7-21. |
| [22] | Yin X Y, Zhang S X, Zhang F. 2013. Two-term elastic impedance inversion and Russell fluid factor direct estimation method for deep reservoir fluid identification[J]. Chinese J. Geophys. (in Chinese), 56(7): 2378-2390, doi: 10.6038/cjg20130724. |
| [23] | Zhang J J, Li H B, Liu H S, et al. 2010. Accuracy of dry frame models in the study of rock physics[J]. Progress in Geophysics (in Chinese), 25(5): 1697-1702, doi: 10.3969/j.issn.1004-2903.2010.05.024. |
| [24] | Zhang J Q, Qu S L, Sun J G, et al. 2010. A fluid substitution realization method in carbonate reservoir[J]. Oil Geophysical Prospecting (in Chinese), 45(3): 406-409, 422. |
| [25] | Zhang Z, Yin X Y, Hao Q Y. 2014. Frequency-dependent fluid identification method based on AVO inversion[J]. Chinese J. Geophys. (in Chinese), 57(12): 4171-4184, doi: 10.6038/cjg20141228. |
| [26] | Zhou S S, Zhang B, Wu X Y. 2009. Research on fluid substitution method and its application[J]. Progress in Geophysics (in Chinese), 24(5): 1660-1664, doi: 10.3969/j.issn.1004-2903.2009.05.015. |
| [27] | Zhou W, Yang H X. 2005. Effects of fractures of rock on elastic property of rock and velocity-porosity relation[J]. Oil Geophysical Prospecting (in Chinese), 40(3): 334-338. |
| [28] | 陈信平, 刘素红. 1996. 浅谈Gassmann方程[J]. 中国海上油气(地质), 10(2): 122-127. [5] 甘利灯. 2003. 四维地震技术及其在水驱油藏监测中的应用[博士论文]. 北京: 中国地质大学. |
| [29] | 黄为清, 郝召兵, 伍向阳. 2011. 一种带误差校正的横波速度预测方法[J]. 地球物理学进展, 26(6): 2184-2189, doi: 10.3969/j.issn.1004-2903.2011.06.036. |
| [30] | 李宏兵, 张佳佳, 姚逢昌. 岩石的等效孔隙纵横比反演及其应用[J]. 地球物理学报, 56(2): 608-615, doi: 10.6038/cjg20130224. |
| [31] | 李维新, 史謌, 王红,等. 2007. 岩石物理弹性参数规律研究[J]. 地球物理学进展, 22(5): 1380-1385, doi: 10.3969/j.issn.1004-2903.2007.05.007. |
| [32] | 李维新, 王红, 姚振兴,等. 2009. 基于约束条件横波速度反演和流体替代[J]. 地球物理学报, 52(3): 785-791. |
| [33] | 李燕, 刘浩杰, 王玉梅. 2010. Gassmann模型机理分析及其应用[J]. 勘探地球物理进展, 33(1): 16-20. |
| [34] | 刘立峰, 孙赞东, 韩剑发,等. 2014. 量子粒子群模糊神经网络碳酸盐岩流体识别方法研究[J]. 地球物理学报, 57(3): 991-1000, doi: 10.6038/cjg20140328. |
| [35] | 宋洪勇, 熊晓军, 林凯,等. 2010. 碳酸盐岩生物礁储层的流体替换研究[J]. 长江大学学报(自然科学版), 7(1): 47-50. |
| [36] | 孙福利, 杨长春, 麻三怀,等. 2008. 横波速度预测方法[J]. 地球物理学进展, 23(2): 470-474. |
| [37] | 王彦仓, 杜维良, 刘喜恒,等. 2014. 利用测井数据实现横波速度的反演及应用效果分析[J]. 地球物理学进展, 29(4): 1798-1802, doi: 10.6038/pg20140441. |
| [38] | 邬龙, 刘堂晏, 王红涛,等. 2014. 干岩石模量的计算方法对比分析及其应用[J]. 地球物理学进展, 29(5): 2272-2277, doi: 10.6038/pg20140542. |
| [39] | 熊晓军, 吕龑, 林凯,等. 2012. 一种碳酸盐岩流体替换新方法[J]. 中国石油大学学报(自然科学版), 36(6): 57-61, doi: 10.3969/j.issn.1673-5005.2012.06.010. |
| [40] | 杨顶辉, 张中杰, 滕吉文,等. 2000. 双相各向异性研究、问题与应用前景[J]. 地球物理学进展, 15(2): 7-21. |
| [41] | 印兴耀, 张世鑫, 张峰. 2013. 针对深层流体识别的两项弹性阻抗反演与Russell流体因子直接估算方法研究[J]. 地球物理学报, 56(7): 2378-2390, doi: 10.6038/cjg20130724. |
| [42] | 张佳佳, 李宏兵, 刘怀山,等. 2010. 几种岩石骨架模型的适用性研究[J]. 地球物理学进展, 25(05): 1697-1702, doi: 10.3969/j.issn.1004-2903.2010.05.024. |
| [43] | 张金强, 曲寿利, 孙建国,等. 2010. 一种碳酸盐岩储层中流体替换的实现方法[J]. 石油地球物理勘探, 45(3): 406-409, 422. |
| [44] | 张震, 印兴耀, 郝前勇. 2014. 基于AVO反演的频变流体识别方法[J]. 地球物理学报, 57(12): 4171-4184, doi: 10.6038/cjg20141228. |
| [45] | 周水生, 张波, 伍向阳. 2009. 流体替换方法研究及应用分析[J]. 地球物理学进展, 24(5): 1660-1664, doi: 10.3969/j.issn.1004-2903.2009.05.015. |
| [46] | 周巍, 杨红霞. 2005. 岩石裂隙对岩石的弹性性质及速度—孔隙率关系的影响[J]. 石油地球物理勘探, 40(3): 334-338. |
 2015, Vol. 30
2015, Vol. 30

