地球物理学进展  2015, Vol. 30 Issue (5): 2113-2119   PDF    
引用本文
周德帅, 刘复刚, 王建, 李广文, 赵业思, 雷超. 2015. 太阳轨道运动恒星周期的证明及其与太阳活动周的对应关系[J]. 地球物理学进展, 30(5): 2113-2119, doi: 10.6038/pg20150515  
ZHOU De-shuai, LIU Fu-gang, WANG Jian, LI Guang-wen, ZHAO Ye-si, LEI Chao. 2015. Verification for the sidereal period of Sun's motion and its corresponding relationship with solar cycles. Progress in Geophysics, 30(5): 2113-2119, doi: 10.6038/pg20150515   
太阳轨道运动恒星周期的证明及其与太阳活动周的对应关系
周德帅1, 刘复刚1,2, 王建1 , 李广文2, 赵业思1, 雷超1    
1. 南京师范大学地理科学学院, 南京 210046;
2. 齐齐哈尔大学理学院地理系, 齐齐哈尔 161006
收稿日期: 2015-03-18 修回日期: 2015-06-28.
基金项目: 国家自然科学基金(41101372,41271204)和江苏高校优势学科建设工程资助项目(164320H101)联合资助.
作者简介: 周德帅,男,1989 年生,硕士研究生, 研究方向为全球变化.( E-mail: wersan@sina.com)
通讯作者: 王建, 男,教授.( E-mail: jwang169@vip.sina.com)
摘要: 基于刘复刚和王建(2013)创建的行星会合指数(K),已经给出了太阳绕太阳系质心的运动轨迹,并得到其恒星周期为准22年.这一恒星周期是根据行星系统中按各自行星质量权重求得的23.77208年周期与通过图像获得的19.8585年行星会合周期的平均值得到的.因为各行星的周期都是恒星周期,故本文通过对K2函数求导方法得到的23.36886年周期也是恒星周期,它与23.77208年周期近似相等,这进一步证实太阳轨道运动恒星周期与由行星系统质心运动所指代的会合周期不同,二者之差异可能与坐标系的选择有关.顾及太阳质心的动与不动两种情况,选取其平均值22.33年作为太阳轨道运动的恒星周期.结果发现,这一周期与太阳活动22.20年磁周期一致.这表明通过修正后的太阳轨道运动特征图像可以近似预测太阳活动和相应时间尺度的气候变化.
关键词: 行星会合指数     太阳轨道运动     恒星周期     太阳活动周    
Verification for the sidereal period of Sun's motion and its corresponding relationship with solar cycles
ZHOU De-shuai1, LIU Fu-gang1,2, WANG Jian1 , LI Guang-wen2, ZHAO Ye-si1, LEI Chao1    
1. College of Geographical Sciences, Nanjing Normal University, Nanjing 210023, China;
2. College of Science, Qiqihar University, Qiqihar 161006, China
Abstract: The planetary synodic index (K) was created (Liu F G & Wang J, 2013), based on it, the quasi-22 yr sidereal period of the Sun's motion round the mass center of solar system was given.It's the average of 23.77208 years calculated by weight function of quality and 19.8585 years according to the image of the planetary synodic index. Since every planetary cycle is the sidereal period, so we also obtained the sidereal period of 23.36886 years by taking the derivatives of the function K2.The results of two methods are almost the same.That offers a new perspective to confirm the difference of synodic period between the sidereal period of the Sun's trajectory and the path of planetary system mass center, the internal connection between the two is which coordinates you use. So on the basis of the two cases that whether the sun's mass center moves, we take their average which is 22.33 years as the sidereal period of orbital motion of Sun, and we find that the result agrees well with the 22.20 years magnetic cycle.This shows that by revising the feature image of Sun's orbital motion, it is possible for us to predict solar activity and climate change with the corresponding time scale.
Key words: planetary synodic index     orbital motion of Sun     sidereal period     solar activity cycles    
 0 引 言

根据太阳活动器测数据和相关太阳活动替代性指标数据检测分析结果皆呈现出最明显的准11年周期(李可军，2004；腊占生，2006)，因此多数研究者将关注点集中在太阳活动的11年周期上.众所周知，太阳黑子活动周期是11.1年(Schwabe-Wolf周期)，就太阳黑子磁场极性而言，太阳活动具有准22.2年磁周期特征.刘复刚和王建等(2014a)研究表明，欲分析太阳黑子磁场极性变化应采用黑子磁场极性图像分析更为科学有效.Jose(1965)、杨志根和赵铭(1988)、刘复刚和王建(2013a，2014b)、McCracken等(2014)都给出了形态特征完全一致的太阳轨道运动轨迹.将太阳黑子活动的磁场极性图像与太阳轨道运动图像进行对比发现，太阳轨道运动特征具有准20年周期，而太阳活动的磁周期是平均22.20年，二者周期存在2年多的相位差.Jose(1965)曾给出两者的对应关系，发现太阳活动与太阳轨道运动角动量变化特征在近期时段有较好的对应.然而，当时间尺度放大后其对应的相位差越来越大.根据最新的太阳黑子磁场极性资料(曲维政，2008)发现与Jose(1965)给出的太阳黑子活动周期在10-11-12活动周期的相位存在较大差异.即使抛开这些因素也无法回避准20年太阳轨道运动周期对太阳黑子活动22.20年周期间存在的相位差问题.刘复刚和王建(2013a)就太阳绕太阳系质心绕转的周期进行了改正，提出了不能将太阳视为分别和每个行星绕二体质心的绕转运动，而应该是太阳和行星系质心同步绕太阳系质心运动的思想.刘复刚和王建(2014c)考虑将水星、金星、地球和火星以及卫星的质量可能对太阳恒星周期的影响，根据开普勒第3定律巧妙地将这些因素考虑进去，并对2013年给出的改正系数进行了修正，进而得到修正系数q=1.11518，并得到太阳轨道运动的恒星周期为22.1826年(约为22.20年)，这与太阳黑子活动的磁周期一致.这在理论上解决和修正了太阳轨道运动周期与太阳黑子活动磁周期间存在的相位差问题.杨志根和赵铭(1988)在分析太阳极性黑子相对数sp周期性变化时指出：“太阳黑子活动在相当程度上是受到了行星运动所导致的日心轨道运动的牵制……，说明了太阳黑子活动的周期性重复不是本身固有的，而是随角动量变率的周期性变化而变化，其变化周期约为178年”.太阳活动与修正后的太阳轨道角动量变化有较好的对应(刘复刚和王建，2014c)，这应该是太阳轨道角动量对太阳活动具有调控作用之观点的理论基础.

根据刘复刚和王建(2013a)创建的行星会合指数K方程(如(1)式)，进而获得行星系质心绕太阳不动点的运动轨迹，如图 1.K方程公式为

其中，K/ri/φi/ωi分别为行星会合指数(K ≥0)、以各自行星质量为权重的平均轨道半径、行星初始日心经度、平均角速度.

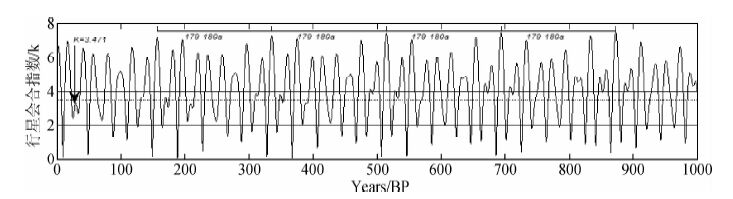
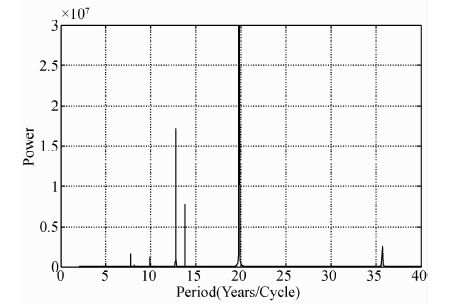
图 1具有显著的179~180年准周期.这样的周期是由9个准19.86年周期构成.这与图 2行星系统质心绕太阳质心(不动点)半径长度变化的傅立叶分析频谱图中检测出的最强周期一致.

图 1 行星系统质心绕日不动点运动轨迹图像(原点：2000AD) Fig. 1 The path of planetary system mass center orbiting the fixed point of the sun

图 2 行星系统质心绕日不动点半径长度变化的傅立叶分析频谱图 Fig. 2 Analysis of Fourier spectrum of the varying lengths of the planetary system mass center orbiting the fixed point of the sun

根据行星会合指数(K)图像分析得到的8大行星绕太阳不动点的平均会合周期为19.8585年，该周期等于太阳系中最大行星木星和第二大行星土星的会合周期.

Jose(1965)指出整个太阳系的角动量守恒.刘复刚和王建等(2013b，c)据此得到推论：太阳自转和太阳绕太阳系质心绕转的角动量之和守恒(JS+JSC=const).为获得准确的太阳轨道运动角动量变化，就必须科学标定太阳轨道运动的周期.本文基于对K指数平方函数(K2)求导的方法从另一种角度进一步证实了太阳轨道运动的恒星周期的存在并与刘复刚和王建(2013a，2014c)获得的太阳轨道运动恒星周期近似.

1 对K指数平方函数(K2)求导

因为K≥0，所以K2标定的曲线极值特征和K指数标定的曲线极值特征具有相位的一致对应性.为此将(1)式改写成形如(2)式的表达式为

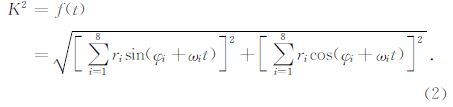
研究表明，行星系质心(P)和太阳(S)质心位置关系主要取决于地外4颗大质量行星(木星、土星、天王星和海王星)的质量权重半径(刘复刚和王建，2013a)，由此将(2)式又简化成(3)式为

对f(t)求导得(4)式为
令f′(t)=0，因为图 1中行星会合指数的峰值和谷值完全可以近似看成峰值-谷值-峰值-谷值…的连续分布状态.因为K≥0，所以函数的极值就对应函数的极值.曲线在f′(t)=0处，意味着行星高度会合(即日心经度似相等，4大行星近似呈直线排列的程度达到极大值)或高度分离(即木星和其它3颗大行星日心经度相差近180°).其实，这样的情形正对应行星系质心绕转半径K的径向加速度为零的时候，就地外4可大质量行星而言，这时也是处在太阳轨道运动所受外力影响的极值状态.在(4)式中，因为(ωj-ωi)≠0，所以理论上，行星会合指数K具有极值时，则存在(5)式中6个方程皆为零的情况，即
因此得(6)式为
当(5)式中各式都具有相同的角值时，就可以得到
因此，可根据等比定理得(8)式.并应用(8)式确定地外4颗大质量行星具有最大会合程度和最大相背离程度的时间点.公式(8)为
当k=0，1，2，…，n时分别得到：t0=11.61518，t1=23.29961，t2=34.98404，……，tn=11.68443n+11.61518.上述各点f′(t)=0是所对应的极值特征时间点，出现这样特征点的平均周期为T1，公式为
T1=t2-t1=t1-t0=34.98404-23.29761=23.29761-11.61518=11.68443
根据图 1图像峰值和谷值特征，可以获得行星系质心距太阳距离的平均极大值或极小值周期T2为
T2=t2-t0=34.98404-11.61518=23.36886年.

2 太阳轨道运动的恒星周期

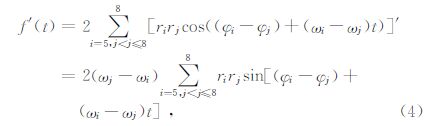
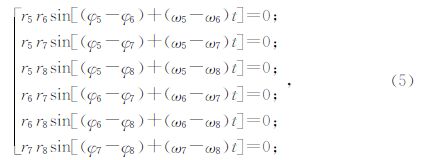
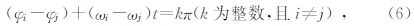
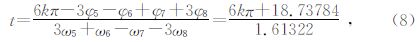
因为23.36886年周期完全是根据行星的恒星周期求得的，而我们通过式(1)给出的图 1主要是地外4颗大质量行星相对太阳不动点的会合周期为19.8585年.如果将8颗行星视为一颗行星，其前提就是行星系统(主要是地外4颗行星)在太阳一侧呈近似直线排列的高度会合状态，因为行星的会合周期一定是行星系统构成恒星周期的必要条件.而作为整个太阳系，太阳和行星系质心是绕太阳系质心同步运动的，因此太阳轨道运动的恒星周期就应该和行星系质心的运动周期一致，所以综合考虑太阳相对太阳系质心的动与不动这一因素，并考虑根据各自行星质量权重求得恒星周期23.77208年.我们把太阳轨道运动的恒星周期视为三者的平均值，即

T=(23.77208+23.36886+19.8585)/3=22.3332(年).

3 根据恒星周期修正的太阳轨迹与太阳活动周的对应关系

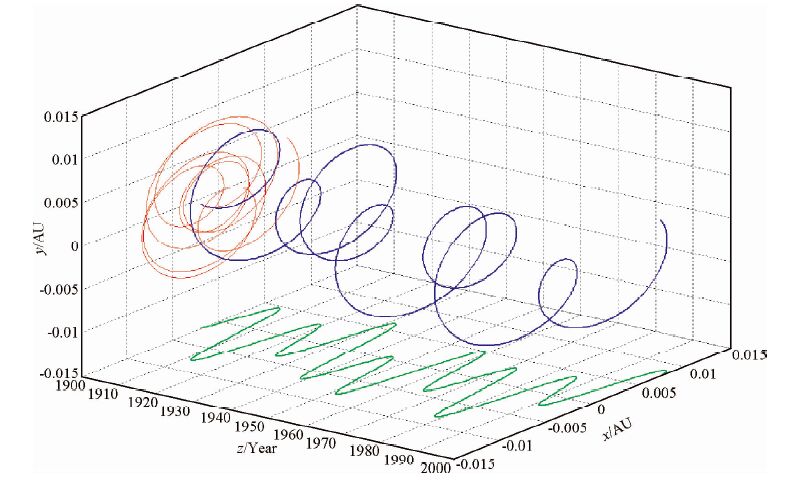
这里把22.3332年周期视为太阳黑子活动的平均磁周期，该周期的1/2长(11.17年)就是太阳黑子活动的准周期.这两个求证结果不仅和已有的分析结果较为接近(Zaqarashvili，1997; Tlatov，2007；Wolff，2010；Abreu et al.，2012；McCracken et al.，2014)而且和前人通过观测太阳黑子数和太阳黑子磁场极性指数获得的周期基本一致.这时如果用行星会合指数K指代太阳轨道运动的恒星周期就应该对横坐标轴或各行星轨道角速度进行相应的调整，其调整系数为1.1246(22.3332/19.8585).图 3(参照Scafetata，2014年文中图 3的B图)是通过调整系数1.1246调整后的太阳绕转太阳系质心运动轨迹的三维图像.太阳黑子活动准11年周期的背景是准22年的Hale磁周期(Hale，1908).根据黑子磁极性来划分太阳活动周期就是黑子活动周期的两倍，太阳活动22年磁周期在蒙德极小期时也比11年的黑子周期更加明显和连续(Usoskin，Mursula，and Kovaltsov，2000).把依次相邻的太阳活动周每两个划为一对，单独绘出太阳活动准22年时间所对应的太阳轨道运动轨迹图，如图 4.在准22年时段内，太阳都绕过太阳系质心约一周，且形态上具有总体的相似性，通过计算每对太阳活动周中太阳质心距离太阳系质心的最小距离，并对持续时间进行统计(见表 1).在1849年前，太阳黑子的观察数据有大量缺口，由于太阳黑子分布具有上升快速和缓慢下降的特征，所以随着缺失数据增多，在太阳活动准22年时段内太阳距太阳系质心的极小值确定存在较大误差(Usoskin and Mursula，2003)，因此我们从第7和8周开始统计.表 1显示每个相邻太阳活动周内的太阳质心距离太阳系质心最小值变化很大，除第15和16周，其他8组中当太阳质心距离太阳系质心最小值较小时，对应的准22年周期持续时间也较短；反之当距离较大时，对应的周期持续时间就较长，这在第5和6周也得到印证，此外这8组中的太阳质心到太阳系质心距离极小值的变化与对应磁周期长度的相关系数也达到0.7741.其原因可能是当太阳向太阳系质心靠近时，太阳轨道运动速度变慢，而当太阳距太阳系质心由近逐渐远离时，运动速度会加快，最终使得这样的周期持续时间变短，通过图 4也可看出，太阳质心轨迹在远离太阳系质心时，以1年为单位时间的步长远比靠近时的步长长.至于第15和16周出现的不符合，可能是受到太阳活动的长周期影响，由于根据修正后的行星会合指数(K)能够把太阳质心的运动轨迹提前绘制，这也就为预测太阳活动周的强度和持续时间提供了可能和便利，根据表 1中第23和24太阳周对距离太阳系质心最小值再次达到较大值，从而认为这一周期将较第21和22持续更长时间，接近24年.这与Solheim(2013)预测的本世纪初的太阳黑子周期将会更长结论基本吻合.而上述求证的磁周期和太阳黑子两个活动周与太阳质心距离太阳系质心距离关系亦可以从图 5的对应关系中得到证实.根据图 5中的对应关系看，太阳黑子奇数周和偶数周个数分别和太阳轨道运动周期的峰值和谷值的个数具有一一对应关系.太阳黑子活动的峰值和谷值的相位和太阳轨道运动周期的相位并不完全吻合，但偶数周的太阳黑子磁场极性指数(MI)绝对值极大与太阳系质心旋出太阳本体所对应的时期有很好的对应关系，如图 5中的浅灰色柱所示(刘复刚和曲维政等，2014b)，这有待进一步研究和探索.为体现图 4的连贯性和表 1相关内容的对应关系，我们绘出图 6以呈现太阳活动准22年周期中太阳到太阳系质心距离极小值的统计规律与调整后的太阳轨道运动图像特征标识的一致性.图 6中，太阳质心到太阳星系质心的最短距离就是会合指数K的极小值，从图中1989.4年、1945.0年和1832.8年和K极小值对应关系看，修正后的太阳轨道运动特征完全可以近似预测太阳活动周强弱和太阳系质心在太阳本体中滞留的时间.

图 3 1900到2000年太阳质心绕太阳系质心运动(修正后)的三维图像 Fig. 3 The trajectory(revised)of the mass center of the Sun round the mass center of solar system from 1900 to 2000

表 1 太阳活动周时段与太阳质心绕太阳系质心运动特征 Table 1 The lengths of group solar activity cycles as defined using minima(Min) and the features of Sun’s motion round the mass center of solar system

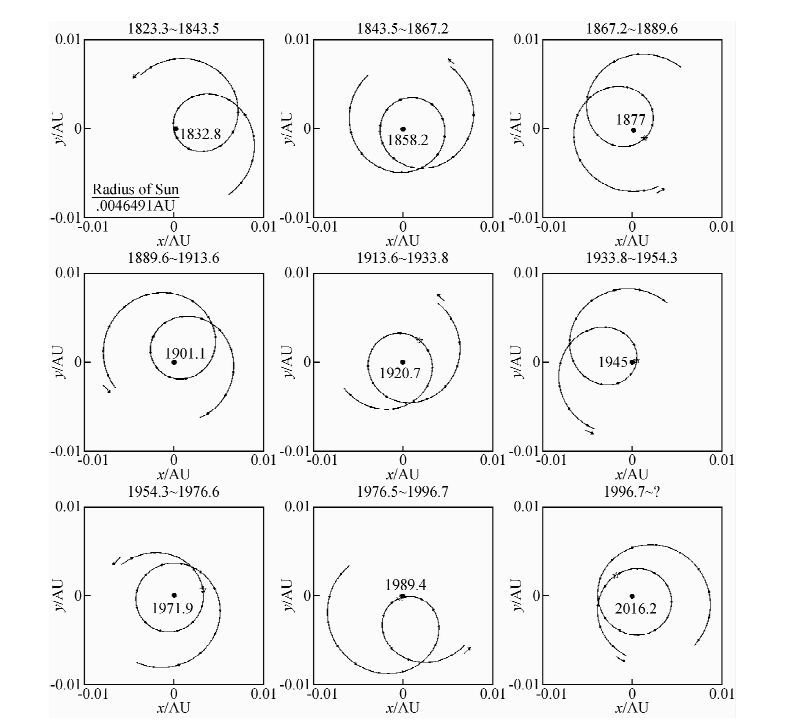
图 4 依次相邻的两个太阳活动周对应的太阳绕太阳系质心运动(修正后)的图像(第一张图中左下方标出太阳半径长度，中间点处为太阳系质心，每段曲线为一年运行的轨迹，距离最近时间已经标出，长度单位为一个天文单位) Fig. 4 The trajectory(revised)of the mass center of the Sun round the mass center of solar system corresponding to each adjacent couple cycles(At the lower left of the first drawing is a line which represents the sun’s radius，the middle dots represents the mass center of solar system，each part curve is the path of Sun within a year，numbers along the curve refer to the dates which is the nearest of the mass center of solar system，the unit of length is the astronomical unit

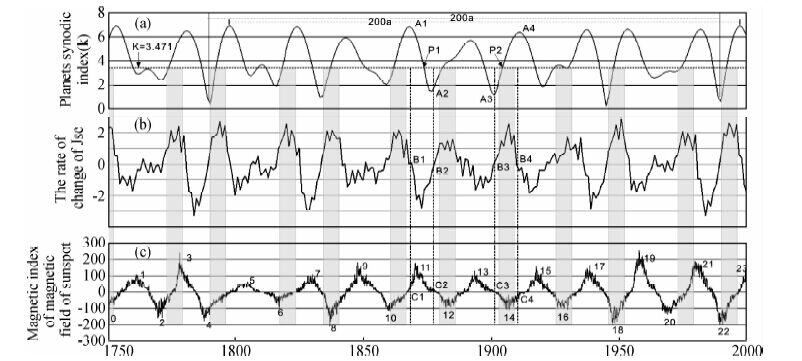
图 5 行星会合指数所指代的太阳绕太阳系质心运动轨迹(a)、太阳轨道运动角动量(b)和太阳黑子磁场极性指数变化曲线(c)的对比(刘复刚等，2014c) Fig. 5 Comparison between the trajectory of Sun around the mass center of solar system，the angular momentum of Sun’s orbital movement and changes of sunspot magnetic index

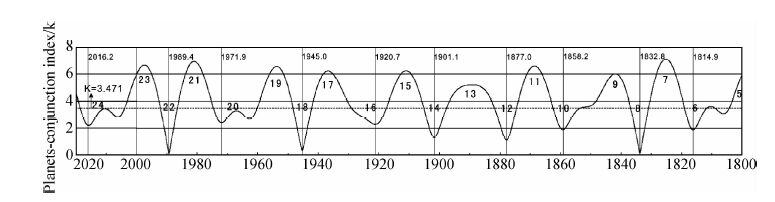
图 6 太阳活动准22年周期中太阳到太阳系质心距离极小值的统计规律与调整后的太阳轨道运动图像特征标识的一致性 Fig. 6 The consistency of statistical regularities of minimum distance within quasi-22 yr of solar activity and the revised orbital motion of Sun
3 结论与探讨

根据之前创建的行星会合指数K运动学方程(或行星会合指数K表达式)，可以间接指代太阳绕太阳系质心的运动轨迹.这将看似极其复杂的行星系统与太阳的位置关系归结到行星系质心和太阳间的二体运动来讨论，而且从已知的所有公开的8大行星天体物理数据出发，创建了行星系统质心绕太阳不动点的运动学方程.这一方程可以从物理机制上阐明行星系统和太阳的关系，并大大简化了以往太阳轨道运动的复杂模型.它的更深层意义是可以给出太阳受行星系统引力作用的周期性变化：当行星系统高度会合在太阳一侧近似呈直线排列时，如果对太阳引力起主要作用的木星、金星、地球和水星也集聚在同一方向，则太阳受到极大的外引力作用；反之，当木星和金星、地球、水星分居在太阳的两侧近似直列，且正值行星系统处于高度相背离状态时，太阳受到的外引力可达到极小值.这种引力作用的极值状态也具有准22年周期，这可以对Tlatov(2007)研究表明的太阳自转运动具有22年的扭摆振动周期给出合理的物理解释.而通过对比太阳质心距离太阳系质心最短距离和依此相邻的两个太阳活动周持续时间，发现当最短距离较小时，对应的这对太阳活动周持续时间就较短；反之，最短距离较大时则对应更长的持续时间.此外，太阳黑子活动的峰值分别和太阳轨道运动K指数的峰值和谷值个数一一对应，这也为进一步探讨太阳黑子22年磁周期规律找到一种可能的途径.

致 谢 感谢审者的支持帮助.

参考文献
[1] Abreu J A, Beer J, Ferriz-Mas A, et al. 2012. Is there a planetary influence on solar activity[J]. Astron. Astrophys, 548, A88.doi: 10.1051/0004-6361/201219997.
[2] Li K J,Su T W,Liang H F.2004.The modern observation for the period of sunspot activity[J].Chinese Science Bulletin (In Chinese), 004,49:2511-2516.
[3] Liu F G, Wang J, Bao K S, et al. 2014a. Hallstatt cycle and variation prediction of the solar activity cycle[J]. Progress in Geophysics, 29(4): 1503-1511,doi: 10.6038/pg20140404.
[4] Liu F G, Qu W Z, Wang J, et al. 2014b. Orbital motion and magnetic variation of Sun: Relation to 22-year cycle of the upper atmospheric temperature of Earth [J]. Progress in Geophys (In Chinese), 29(02):0512-0517.
[5] Liu F G, Wang J. 2014c. The 22-year cycle of solar revolution round the solar mass center and its relation with the solar activity[J]. Chinese Journal Geophysics, 57(11): 3834-3840, doi: 10.6038/cjg20141137.
[6] Liu F G, Wang J. 2013a. Changes of the planet juncture index and solar revolution cycle around the mass center of the solar system[J]. Chinese J. Geophys. (In Chinese), 56(5):1457-1466.doi: 10.6038/cjg20130504.
[7] Liu F G, Wang J, Shang Z Y, Zheng Y. 2013b. Study on long-term cyclical rhythm of solar activity[J]. Progress in Geophys(In Chinese),28(2):570-578.doi: 10.6038/pg20130205.
[8] Liu F G, Wang J, Bai S B, Shang Z Y.2013c. The planetary motion and the change of 22 year cycle the Sun spin velocity. [J].Progress in Geophysics.28 (4): 1678-1683, doi:10.6038/pg20130406.
[9] McCracken K G, Beer J, &Steinhilber F. 2014. Evidence for Planetary Forcing of the Cosmic Ray Intensity and Solar Activity Throughout the Past 9400 Years[J]. Solar Physics, 289(8):3207-3229. doi:10.1007/s11207-014-510-1.
[10] Paul D. Jose. 1965. Sun’s Motion and Sunspots [J]. The Astronomical Journal, 70(3): 193-200.
[11] QuWeizheng, Qin ting, Deng Shenggui, Du ling. 2008. The time sequence of the magnetic index of the sunspot magnetic field[J].Progress in Geophysics, 23(6): 1727-1735.
[12] Scafetata, N. 2014.The complex planetary synchronization structure of the solar system[J].Pattern Recogn.Phys.,2,1-19.doi:10.5194/prp-2-1-2014.
[13] Solheim, J. E. 2013.The sunspot cycle length-modulated by planets[J]. Pattern Recogn. Phys1, 159-164.
[14] Tlatov A G. 2007,22-year variations of the solar rotation and solar activity cycles[J]. AstronLett+, 33:771-779. doi: 10.1134/S1063773707110084.
[15] Usoskin, I. G. & Mursula, K. 2003.Long-term solar cycle evolution: review of recent developments [J]. Solar Physics, 218, 319-343.
[16] Usoskin, I. G., Mursula, K. &Kovaltsov, G. A. 2000.Cyclic behaviour of sunspot activity during the Maunder Minimum[J]. Astronomy and Astrophysics, 354, L33-L36.
[17] Wolff C L, &Patrone P N. 2010. A new way that planets can affect the Sun[J]. Solar Physics, 266(2), 227-246.
[18] Yang Z G. &ZhaoM.1988. An investigation for the Cause of Formation of the Major Period of the Relative Sunspot Numbers with Bipolarity[J]. ActaAstronomicaSinica (In Chinese), 29, 297.
[19] Zaqarashvili, T. V. 1997. On a possible generation mechanism for the solar cycle[J]. The Astrophysical Journal, 487(2), 930.
[20] Zhan L S,He J M,Ye Y L,Zhao H J.2006.Periodicity analysis of solar activity by wavelet analyzing method[J].ActaAstronomicaSinica (In Chinese),47(2):166-174.
[21] 李可军,苏同卫,梁红飞.2004.现代黑子观测的太阳黑子活动的周期性[J].科学通报, 49:2511-2516.
[22] 刘复刚,王建,鲍锟山,等.2014a. 太阳活动Hallstatt周期及太阳活动周强弱变化的预测[J]. 地球物理学进展,29(4): 1503-1511,doi: 10.6038/pg20140404.
[23] 刘复刚,曲维政,王建,等. 2014b.太阳轨道运动-太阳磁场变化与地球高层大气温度准22年周期循环的联系[J].地球物理学进展,29(2):0512-0517,doi:10.6038/pg20140206.
[24] 刘复刚,王建.2014c. 太阳绕太阳系质心运动22年周期及其与太阳活动的联系[J].地球物理学报,57(11): 3834-3840,doi: 10.6038/cjg20141137.
[25] 刘复刚,王建.2013a.行星会合指数变化与太阳绕太阳系质心运转的周期[J]. 地球物理学报,56(5):1457-1466,doi: 10.6038/cjg20130504.
[26] 刘复刚,王建,商志远,郑一. 2013b.太阳轨道运动长周期性韵律的成因[J]. 地球物理学进展,28(2):0570-0578,doi: 10.6038/pg20130205.
[27] 刘复刚,王建,白世彪,商志远. 2013c. 行星运动与太阳自转角速度22年周期变化[J]. 地球物理学进展,28(4): 1678-1683,doi: 10.6038/pg20130406.
[28] 杨志根,赵铭.1988.太阳极性黑子相对数主周期的成因探讨[J]. 天文学报,29(3): 297-304.
[29] 占腊生,何娟美,叶艺林.2006.赵海娟.太阳活动周期的小波分析[J].天文学报,47(2):166-174.