2. 中国科学院大学, 北京 100049;
3. 中国科学院地质与地球物理研究所, 北京 100029
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
目前,已有不少学者对电磁法的探测深度进行了研究,朱仁学等(2001)对一维情况下MT的探测能力进行了研究,文中采用三层模型,模型第二层作为异常体,最后得出异常体规模越大、与围岩的电性差越大则探测深度越大,但没有对更复杂模型进行进一步研究;薛国强(2004)对瞬变电磁测深的探测深度进行了研究,得出了瞬变电磁法对地探测时存在一个最小深度的结论;王庆乙(2007)对瞬变电磁法回线边长决定探测深度提出了质疑,通过研究认为磁矩只是决定探测结果的信噪比;单春玲等(2008)针对音频范围内人工源电磁测深大探测深度分辨能力作了定性和定量分析,但仅对异常体的埋深及规模进行了研究;朱凯光等(2008)研究了层状模型下频率域航空电磁的探测深度,文中仅对三层模型进行了研究;韩自豪等(2008)研究了瞬变电磁在华北煤田的勘探深度;闫述等(2009)用解析分析、时域有限差分、时-频分析的方法,对瞬变电磁测深法的勘探深度问题做了有价值的研究;李乃民和李东徽(2012)对频率域、时间域电磁法的探测深度和影响因素做了简要总结分析;吴信民等(2013)比较全面地总结分析了前人对电法勘探中探测深度的研究成果.
关于频率域电磁测深的理论探测深度,王卫平和王守坦(2003)给出了直升机频率域航空电磁系统不同装置的理论探测深度;陈明生等(2012)提到趋肤深度等于约化波长,可用于评估频率域电磁测深的探测深度.柳建新等(2012)也提到趋肤深度随频率和介质电阻率变化的情况是开展大地电磁测深勘探工作设计的基础;陈卫营和薛国强(2014)以接地长导线源为例研究了可控源电磁场全域的有效趋肤深度;陈斌等(2014)针对目标层与围岩电性差异不大或目标层引起的异常响应不明显时,基于扩散电场法提出了一种系统探测深度的估算方法,具有理论指导意义;Szarka和Fischer(1989)通过分析二层介质模型地面阻抗实部与虚部曲线,认为相位曲线最后在45°处分离,Spies(1989)以此为依据,提出用1.5倍趋肤深度来估计大地电磁的理论探测深度;但是都是基于二层介质模型,对于多层介质提到用具有相同导电效应的替代层将多层介质转化为二层介质来计算其探测深度,但是并没有用多层模型进行验证,也没有对二维情况进行分析.
本文针对大地电磁法,先从二层介质波阻抗公式出发,证明了二层介质视电阻率曲线的一些特征:第一层相同的二层介质的视电阻率曲线会在几个点相交(从低频到高频依次为第1、2、…交点);第1、2、…交点所对应的频点穿过第一层介质时,振幅分别衰减到地面处幅值的e-π/4、e-3π/4、…、e-[π+2(n-1)π]/4,n=1,2,…;这些交点的位置由第一层介质决定,纵坐标(视电阻率)等于第一层电阻率,横坐标(频率)可由第一层电阻率及厚度计算得到.然后,用二层介质模型进行了验证,分析二层介质视电阻率曲线,认为自第2个交点至更高频的结果几乎不受第二层介质影响,从而提出用振幅衰减到地面处幅值的e-3π/4≈9.48%时的深度来作为均匀半空间的探测深度,即3π/4倍趋肤深度,此时探测深度δ≈1186$\sqrt {\frac{\rho }{f}} $, 其中ρ为电阻率(Ω·m),f(Hz)为频率;接着针对多层介质,提出了等效衰减作用的概念,然后分别用具有等效导电效应、等效衰减作用的替代层将多层介质转换成均匀半空间,从而可以计算多层介质下的探测深度.最后用多层介质及二维模型分别进行了验证,并与趋肤深度及前人提出的1.5倍趋肤深度进行了对比,结果表明,用本文中的2种方法计算探测深度,所有模型都能得到较准确的探测深度,而用趋肤深度或1.5倍趋肤深度作为探测深度误差较大.
1 二层介质分析文中物理量均采用国际单位制.
1.1 衰减因子定义电磁波在地下介质传播中,振幅衰减到地面处幅值的e-α时,有


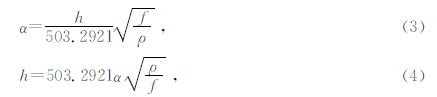
由式(3)可知,Spies(1989)提出来的1.5倍趋肤深度对应的衰减因子α=1.5.
1.2 二层介质视电阻率曲线 1.2.1 理论特征取时谐因子为e-iωt,二层介质地面处的阻抗值为
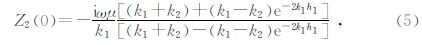
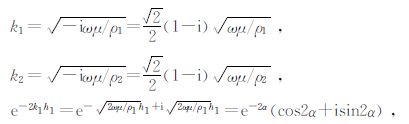
令:
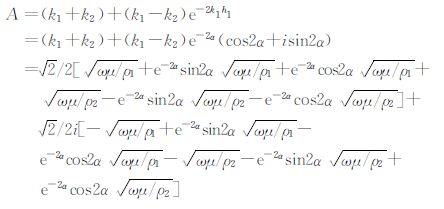
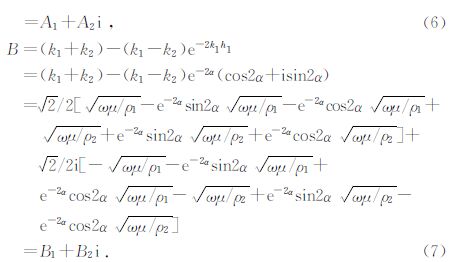
a.当cos2α=0时有

此时由cos2α=0可得衰减系数为
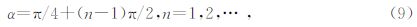
由此可得出结论:
(1)第一层相同的两层介质模型,这些模型的视电阻率曲线会经过相同的几个点,且这些点所对应的视电阻率等于介质第一层的电阻率,而这些点所对应的频点由第一层介质决定,与第二层介质无关;
(2)任意两层模型,从低频到高频这些点依次所对应的频点穿过第一层介质时,衰减因子分别为$\frac{\pi }{4}$、$\frac{\pi }{4}$+1×$\frac{\pi }{2}$、…、$\frac{\pi }{4}$+(n-1)×$\frac{\pi }{2}$,即振幅分别衰减到地面处幅值的e-$\frac{\pi }{4}$、e-$\frac{{3\pi }}{4}$、…、e-$\frac{{\pi + 2\left( {n - 1} \right)\pi }}{4}$.
上述结论与李金铭(2005)二层水平地层上的大地电磁测深曲线特点相符合,从另一方面也证明了其正确性.
此时,可根据式(3)计算得到各交点处的频点为

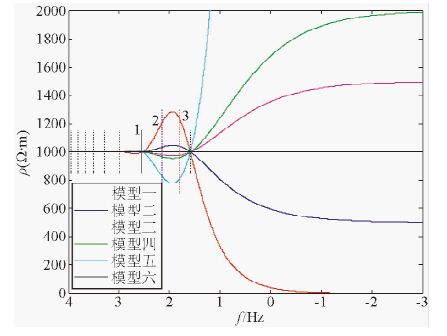
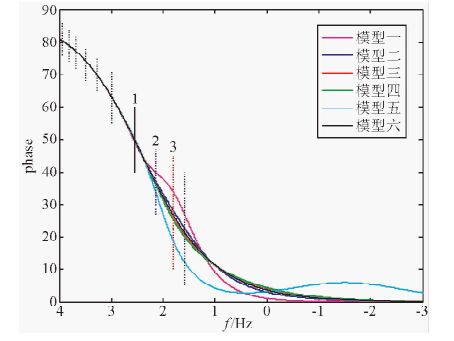
为确定均匀半空间的探测深度,采用二层介质模型,若第二层介质对某个频点的结果恰好没影响,则认为该频点正好探测到第一层与第二层的分界面处.六个第一层相同的二层模型参数:第一层电阻率为1000 Ω·m, 厚度为2000 m, 六个模型第二层电阻率分别为1 Ω·m、500 Ω·m、1500 Ω·m、2000 Ω·m、1201505130 Ω·m、1000 Ω·m.由于受第二层介质影响,这些模型的视电阻率曲线、相位曲线会发生分离.得到的视电阻率曲线及相位图分别如图 1、2所示,图中所有交点都用黑色虚(实)线标出,这些交点处的频点穿透到第一层与第二层的分界面时,从低到高频依次对应的衰减因子为π/4、3π/4、…、15π/4,1号线对应的衰减因子α=3π/4,2、3号线对应的衰减因子α分别为1.5与1.
分析图 1、2,在一定的误差允许范围内,可认为视电阻率曲线、相位曲线在高频段重合直到某个频点才开始分离,第二层介质对该频点及更高频点的结果影响非常有限或没有影响,该频点正好探测到第一层与第二层的分界面处,即在ρ=ρ1的均匀半空间的探测深度为h1,ρ1、h1分别为二层介质第一层的电阻率与厚度.以第一层与第二层的分界面为探测界面,这些交点处频点从低到高频依次对应的衰减因子为$\frac{\pi }{4}$、$\frac{3\pi }{4}$、…、$\frac{15\pi }{4}$.1号线对应的衰减因子α=3π/4,2、3号线衰减因子α分别为1.5与1.从图 1、2可以看出,1号线至更高频点的曲线形态基本重合,2、3号线时曲线已发生较大分离.以ρ=ρ1的均匀半空间为参考,这三种情况下,分别自1、2、3号线处频点至更高频,第二层介质对地面处的视电阻率及相位产生的最大影响(%)见表 1,以视电阻率为例,α=1时受影响最大的频点在假极值处.
|
|
表 1 不同衰减因子时第二层介质视电阻率及相位的最大影响 Table 1 The second layer earth’s maximum influence with different α |
从表中看出,当α=1时,视电阻率及相位的最大影响都超过了28%;α=1.5时,视电阻率的最大影响达到了20%,相位的最大影响超过了5%;α=3π/4时,视电阻率及相位的最大影响均在1%上下.说明用趋肤深度 或Brain于1987年提出的用1.5倍趋肤深度作为理论探测深度并不准确,而用α=3π/4时的深度来作为探测深度是可行的,此时电磁波衰减到地面处振幅的e-$\frac{3\pi }{4}$≈9.48%.由此可得到均匀半空间下的探测深度公式为
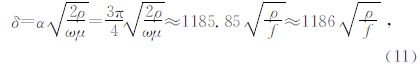
将多层介质通过一定方式等效成均匀半空间.在这里,分别采用具有相同导电效应与等效衰减作用的替代层.
3.1 具有相同导电效应的替代层设有m层,每层电阻率分别为ρ1、ρ2、…、ρm,厚度分别为h1、h2、…、hm,等效层电阻率及厚度分别为ρt、ht.当电流平行于岩层流动时,各层相当于并联电路,由此有


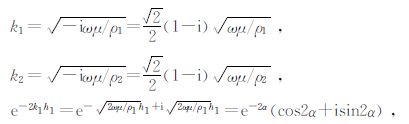
|
图 1 第一层相同的二层模型的视电阻率曲线图 Fig. 1 The apparent resistivity of two-layer earth models with the same first layer earth |
|
图 2 第一层相同的二层模型相位曲线图 Fig. 2 The phase of two-layer earth models with the same first layer earth |
|
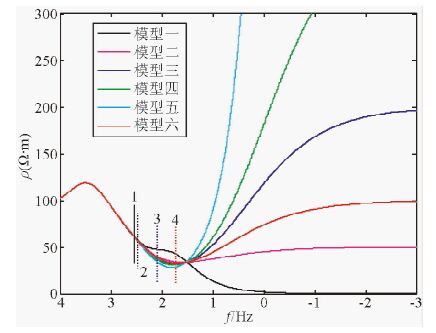
图 3 前四层一样的五层介质的视电阻率图 Fig. 3 The apparent resistivity of five-layer earth models with the same first four-layer earth |
|
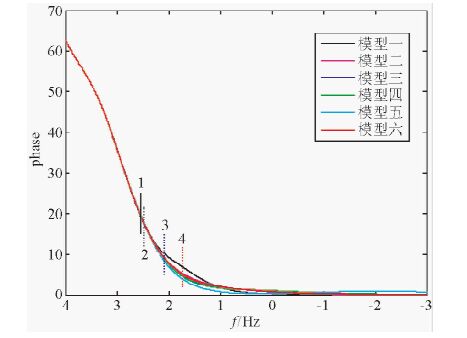
图 4 前四层一样的五层介质的相位图 Fig. 4 The phase of five-layer earth models with the same first four-layer earth |
|
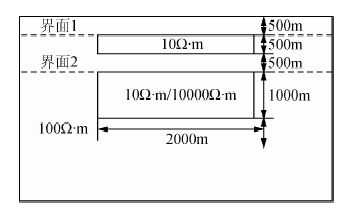
图 5 二维模型 Fig. 5 Two-dimensional earth models |
|
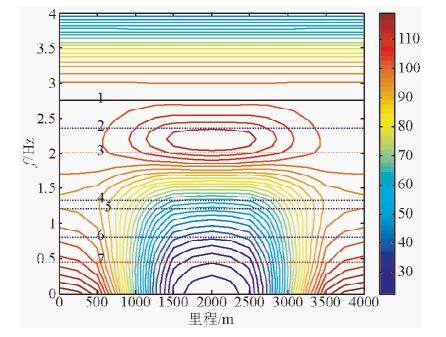
图 6 TM模式下第二个地质体电阻率为10 Ω·m时的视电阻率图 Fig. 6 The apparent resistivity in TM mode when the second geologic body’s resistivity is 10 Ω·m |
|
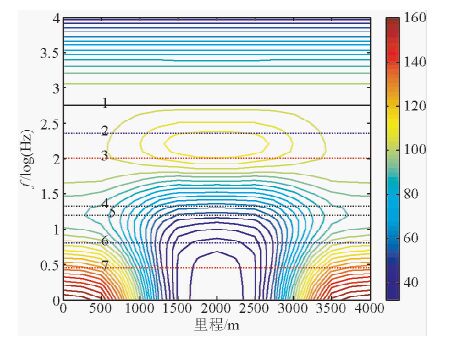
图 7 TM模式下第二个地质体电阻率为1 0000 Ω·m时的视电阻率图 Fig. 7 The apparent resistivity in TM mode when the second geologic body’s resistivity is 10000 Ω·m |
根据式(14),便很容易编写程序计算层状介质模型下任意频点的探测深度,可以先确定该频点探测深度处于哪一层,然后采用二分法即可计算得到探测深度.
3.2 具有等效衰减作用的替代层考虑式(10),在这里提出等效衰减作用的概念.由式(1)可知,两个一层介质,一层电阻率及厚度分别为ρ1、h1,另一层电阻率及厚度分别为ρ2、h2,若满足条件

可将所有层都按等效衰减转换成同一电阻率,然后得到相应的转换厚度,公式为
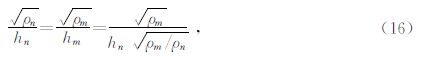
在这里,将其它层的电阻率按等效衰减都转换成第一层的电阻率,此时,多层介质近似探测深度公式为
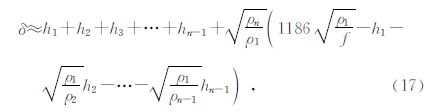
基本思路:采用多个只有最后一层不同的多层介质模型,由于受最下面一层介质影响,这些模型的视电阻率曲线、相位曲线会发生分离.在一定的误差允许范围内,可认为视电阻率曲线、相位曲线在高频段重合直到某个频点才开始分离,最下面一层介质对该频点及更高频点的结果影响非常有限或没有影响,则该频点正好探测到最后一层与前一层的分界面处.
4.1 层状介质模型验证六个前四层一样的五层介质模型参数:前四层电阻率分别为100 Ω·m、150 Ω·m、20 Ω·m、100 Ω·m, 厚度分别为50 m、50 m、200 m、100 m, 六个模型第五层电阻率分别为0.1 Ω·m、50 Ω·m、200 Ω·m、400 Ω·m、120150513 Ω·m、100 Ω·m.得到的视电阻率曲线及相位图分别如图 3、4所示.穿透到最后一层与前一层的分界面处时,图中1、2两条线的衰减因子α=3π/4,分别采用的是等效衰减作用与相同导电效应替代层.3、4号线衰减因子分别为1.5与1,采用的都是相同导电效应替代层.从图 3、4可以看出,1或2号线至更高频点的曲线形态基本重合,3、4号线时的曲线已发生较大分离.
4.2 二维模型验证大地电磁二维正反演已非常成熟(陈小斌等,2005;蔡军涛等,2010;董洁等,2012;刘云和王绪本,2012;叶涛等,2013;陈小斌等,2014).在这里采用有限单元法矩形网格剖分双线性插值进行二维正演,所用二维模型如图 5所示,共两个二维模型,下方地质体电阻率分别为10 Ω·m、10000 Ω·m.以TM模式下视电阻率图为例,如图 6、7所示
如图 5所示两个界面,1、2、3三条线为衰减因子α=3π/4、1.5、1,穿透到界面一时的频点,可以看出1号线恰好不受界面一以下介质的影响,而2、3号线可以明显看出已受界面一以下介质影响;4、5、6、7四条线为α=3π/4、3π/4、1.5及1,穿透到界面二时的频点,其中4号线对应等效衰减替代层,5号线对应相同导电效应替代层.对比图 5、6,可以看出4号线以上的曲线形态几乎完全一致,5号线以上的曲线形态也基本一致,而6、7两条线时的曲线形态已有较大不同.
5 结 论5.1 第一层相同的二层介质的视电阻率曲线会在几个点相交(从低到高频依次为第1、2、…交点);第1、2、…交点所对应的频点穿过第一层介质时,振幅分别衰减到地面处幅值的e-π/4、e-3π/4、…、e-[π+2(n-1)π]/4;这些交点的位置由第一层介质决定,纵坐标(视电阻率)等于第一层电阻率,横坐标(频率)可由第一层电阻率及厚度计算得到.
5.2 对于估计均匀半空间的频率域电磁探测深度,与趋肤深度或1.5倍趋肤深度相比,用振幅衰减到地面处幅值的e-3π/4时的深度更合理,此时探测深度δ≈1186$\sqrt {\rho /f} $, ρ为均匀半空间的电阻率,f为频率.
5.3 对于多层介质或二维情况下的频率域电磁探测深度,用相同导电效应及等效衰减作用的替代层这两种方法均合适.
致 谢 这是我发表的第一篇文章,对父母多年来的辛劳付出表示最真挚的感谢!
| [1] | Cai J T, Chen X B, Zhao G Z. 2010. Refined techniques for data processing and two-dimensional inversion in magnetotelluricⅠ: Tensor decomposition and dimensionality analysis[J]. Chinese Journal of Geophysics (in Chinese), 53(10): 2516-2526, doi: 10.3969/j.issn.0001-5733.2010.10.025. |
| [2] | Chen B, Mao L F, Liu G D. 2014. The estimated prospecting depth of CHTEM-I system by the method of diffusion electric field [J]. Chinese Journal of Geophysics (in Chinese), 57(1): 303-309, doi: 10.6038/cjg20140126. |
| [3] | Chen X B, Zhao G Z, Tang J, et al. 2005. An adaptive regularized inversion algorithm for magnetotelluric data[J]. Chinese Journal of Geophysics, (in Chinese), 48(4): 937-946. |
| [4] | Chen X B, Cai J T, Wang L F et al. 2014. Refined techniques for magnetotelluric data processing and two-dimensional inversion(Ⅳ): Statistical image method based on multi-site, multi-frequency tensor decomposition[J]. Chinese Journal of Geophysics (in Chinese), 57(6): 1946-1957, doi: 10.6038/cjg20140625. |
| [5] | Chen M S. 2012. Analysis of some problems on the detecting depth of frequency electromagnetic sounding [J]. Coal Geology & Exploration (in Chinese), 40(6): 67-70. |
| [6] | Chen W Y, Xue G Q. 2014. Effective skin depth of whole EM field due to a grounded wire source[J]. Chinese Journal of Geophysics (in Chinese), 57(7): 2314-2320, doi: 10.6038/cjg20140725. |
| [7] | Dong J, Wei W B, Ye G F, et al. 2012. Study of two dimensional magnetotelluric inversions of complex three dimensional structures[J]. Chinese Journal of Geophysics (in Chinese), 55(12): 4003-4014, doi: 10.6038/j.issn.0001-5733.2012.12.012. |
| [8] | Han Z H, Wei W B, Zhang W B. 2008. Study on the exploration depth of transient electromagnetic method in northern China coalfield[J]. Progress in Geophysics (in Chinese), 23(1): 237-241 |
| [9] | Li J M. 2005. Electric and Electric Prospecting (in Chinese) [M]. Beijing: Geology Publishing House. |
| [10] | Liu J X, Tong X Z, Guo R W, et al. 2012. Electromagnetic Sounding: Data’s Processing, Inversion and Interpretation (in Chinese) [M]. Beijing: Science Press. |
| [11] | Li N M, Li D H. 2012. Overview about depth of investigation on electromagnetic method[J]. Energy Research and Management (in Chinese), (1): 59-61. |
| [12] | Liu Y, Wang X B. 2012. The FEM for modeling 2-D MT with continuous variation of electric parameters within each block[J]. Chinese Journal of Geophyscs (in Chinese), 55(6): 2079-2086, doi: 10.6038/j.issn.0001-5733.2012.06.029. |
| [13] | Shan C L, Liu G X, Han J T. 2008. Numerical simulation in great depth resolving power of magnetotelluric sounding[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 38(S1): 24-26, 29. |
| [14] | Spies B R. 1989. Depth of investigation in electromagnetic sounding methods[J]. Geophysics, 54(7): 872-888. |
| [15] | Szarka L, Fischer G. 1989. Electromagnetic parameters at the surface of conductive halfspace in terms of the subsurface current distribution[J]. Geophys. Trans., 35: 157-172. |
| [16] | Wang Q Y. 2007. Querying the depth formula of TEMS[J]. Geophysical and Geochemical Exploration (in Chinese), 31(4): 327-332. |
| [17] | Wang W P, Wang S T. 2003. Electromagnetic Response Character of Helicopter Frequency Domain EM System above Uniform Half Space and Its Prospecting Depth[J]. Acta Geoscientia Sinica, (in Chinese), 23(3): 285-288. |
| [18] | Wu X M, Yang H Y, Yang Y X, et al. 2013. Theoretical depth of investigation of electric method prospecting[J]. Journal of East China Institute of Technology (in Chinese), 36(1): 60-64. |
| [19] | Xue G Q. 2004. On surveying depth by transient electromagnetic sounding method[J]. Oil Geophysical Prospecting (in Chinese), 39(5): 575-578. |
| [20] | Yan S, Shi X X, Chen M S. 2009. The probing depth of transient electromagnetic field method[J]. Chinese Journal of Geophysics (in Chinese), 52(6): 1583-1591, doi: 10.3969/j.issn.0001-5733.2009.06.020. |
| [21] | Ye T, Chen X B, Yan L J. 2013. Refined techniques for data processing and two-dimensional inversion in magnetotelluric(Ⅲ): using the Impressing Method to construct starting model of 2D magnetotelluric inversion[J]. Chinese Journal of Geophysics (in Chinese), 56(10): 3596-3606, doi: 10.6038/cjg20131034. |
| [22] | Zhu K G, Lin J, Liu C S, et al. 2008. One-dimensional forwand and prospecting depth for airborne frequency domain electromagnetic method[J]. Progress in Geophysics (in Chinese), 23(6): 1943-1946. |
| [23] | Zhu R X, Zhou Y X, Meng L S, et al. 2001. The study of detecting ability for 1D electrical body with MT method [J]. Journal of Changchun University of Science and Technology (in Chinese), 31(3): 302-305. |
| [24] | 蔡军涛, 陈小斌, 赵国泽. 2010. 大地电磁资料精细处理和二维反演解释技术研究(一)——阻抗张量分解与构造维性分析[J]. 地球物理学报, 53(10): 2516-2526, doi: 10.3969/j.issn.0001-5733.2010.10.025. |
| [25] | 陈斌, 毛立峰, 刘光鼎. 2014. 用扩散电场法估算CHTEM-I系统的探测深度[J]. 地球物理学报, 57(1): 303-309, doi: 10.6038/cjg20140126. |
| [26] | 陈明生. 2012. 关于频率电磁测深几个问题的探讨(二)——频率电磁测深探测深度的几个问题分析[J]. 煤田地质与勘探, 40(6): 67-70. |
| [27] | 陈卫营, 薛国强. 2014. 接地导线源电磁场全域有效趋肤深度[J]. 地球物理学报, 57(7): 2314-2320, doi: 10.6038/cjg20140725. |
| [28] | 陈小斌, 赵国泽, 汤吉,等. 2005. 大地电磁自适应正则化反演算法[J]. 地球物理学报, 48(4): 937-946. |
| [29] | 陈小斌, 蔡军涛, 王立凤,等. 2014. 大地电磁资料精细处理和二维反演解释技术研究(四)——阻抗张量分解的多测点-多频点统计成像分析[J]. 地球物理学报, 57(6): 1946-1957, doi: 10.6038/cjg20140625. |
| [30] | 董洁, 魏文博, 叶高峰,等. 2012. 大地电磁测深二维反演方法求解复杂电性结构问题的适应性研究[J]. 地球物理学报, 55(12): 4003-4014, doi: 10.6038/j.issn.0001-5733.2012.12.012. |
| [31] | 韩自豪, 魏文博, 张文波. 2008. 华北煤田瞬变电磁勘探深度研究[J]. 地球物理学进展, 23(1): 237-241. |
| [32] | 李金铭. 2005. 地电场与电法勘探[M]. 北京: 地质出版社. |
| [33] | 李乃民, 李东徽. 2012. 电磁法探测深度概述[J]. 能源研究与管理, 59(1): 59-61. |
| [34] | 柳建新, 童孝忠, 郭荣文,等. 2012. 大地电磁测深法勘探——资料处理、反演与解释[M]. 北京: 科学出版社. |
| [35] | 刘云, 王绪本. 2012. 电性参数分块连续变化二维MT有限元数值模拟[J]. 地球物理学报, 55(6): 2079-2086, doi: 10.6038/j.issn.0001-5733.2012.06.029. |
| [36] | 单春玲, 刘国兴, 韩江涛. 2008. 大探测深度电磁测深分辨能力的数值模拟[J]. 吉林大学学报(地球科学版), 38(S1): 24-26, 29. |
| [37] | 王庆乙. 2007. 对瞬变电磁法回线边长决定探测深度的质疑[J]. 物探与化探, 31(4): 327-332. |
| [38] | 王卫平, 王守坦. 2003. 直升机频率域航空电磁系统在均匀半空间上方的电磁响应特征与探测深度[J]. 地球学报, 24(3): 285-288. |
| [39] | 吴信民, 杨海燕, 杨亚新,等. 2013. 论电法勘探的理论探测深度[J]. 东华理工大学学报(自然科学版), 36(1): 60-64. |
| [40] | 薛国强. 2004. 论瞬变电磁测深法的探测深度[J]. 石油地球物理勘探, 39(5): 575-578. |
| [41] | 闫述, 石显新, 陈明生. 2009. 瞬变电磁法的探测深度问题[J]. 地球物理学报, 52(6): 1583-1591, doi: 10.3969/j.issn.0001-5733.2009.06.020. |
| [42] | 叶涛, 陈小斌, 严良俊. 2013. 大地电磁资料精细处理和二维反演解释技术研究(三)——构建二维反演初始模型的印模法[J]. 地球物理学报, 56(10): 3596-3606, doi: 10.6038/cjg20131034. |
| [43] | 朱凯光, 林君, 刘长胜,等. 2008. 频率域航空电磁法一维正演与探测深度[J]. 地球物理学进展, 23(6): 1943-1946. |
| [44] | 朱仁学, 周云轩, 孟令顺,等. 2001. MT方法对一维地质体探测能力的研究[J]. 长春科技大学学报, 2001, 31(3): 302-305. |
 2015, Vol. 30
2015, Vol. 30


