强震发生并不是随机的，并不是什么地方都会发生的，强震在空间上具有一定的有序性(许绍燮，2011).环太平洋地震带是典型的板块构造运动边界，从南美洲南端的合恩角起，按逆时针方向沿美洲西岸经阿留申群岛、千岛群岛至日本岛弧.斐济横跨太平洋板块和印度-澳大利亚大陆板块，属于该区南部强地震频发区域之一.随着中国经济进一步发展，我国公民出境休闲游的比例上升，越来越多的人选择斐济作为旅游目的地.当前斐济成为全球最佳十大蜜月旅游基地之一，人流汇聚，因此对斐济地区地震等相关自然灾害趋势判断变得尤为突出.

可公度理论是以天文学上的可公度性为基础，从理论和应用上对其展开研究，进而作为一种预测的方法，该理论略去随机事件的细节数据，将随机变量简化为布尔(BOOL)符号，从时间上描述其统计规律(吕牛顿和张清，1996).因此有必要进行深入研究，丰富研究案例，找寻其中的对称性规律.当前，应用可公度法研究灾害的时空变化规律和对称性特征已有大量成果，此前成功预测了1991年我国江淮重大水灾和1992年美国加州的强烈地震，2008年和2010年的川滇地区地震，以及成功预测了2014年10月7日云南省景谷6.6级地震(翁文波，1981；延军平等，2006；吴梦初和延军平，2013).可公度理论在自然灾害的预测方面具有较好的实际预警和参考意义.鉴此，本文基于可公度理论并结合可公度系图谱和蝴蝶结构图对斐济地区M_S≥7.1地震进行时空对称性及其发生趋势判断分析.旨在探索对称性在地震灾害趋势判断中的意义，丰富可公度方法的灾害趋势判断案例.同时辅助有关部门积极应对重大地震灾害，减少社会、经济等各方面的损失，提供一些可供参考的依据.

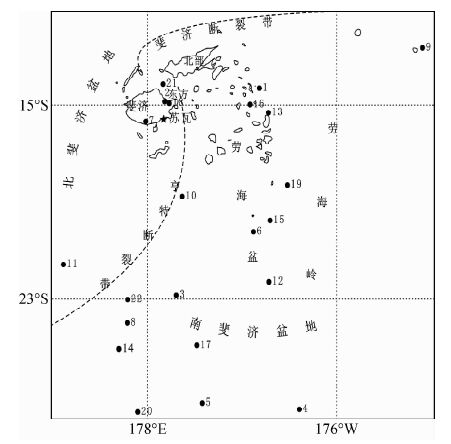
斐济地处南太平洋(图 1)，180°经线贯穿其中，属热带海洋性气候，四季如春，全年适合旅游，是世界著名的度假胜地、旅游天堂.首都苏瓦是南太平洋著名的天然良港，素有南太平洋文化十字路口之称.地震是该区域一种常见的自然灾害，自1962年以来斐济地区共发生M_S≥7.1地震22次，其中8次地震发生在斐济群岛上.因此研究斐济地区地震规律，预测下一次地震的发生年份和大体区域，对全球旅游者和当地政府都有较好的预警和防范作用.

斐济地处于环太平洋地震带上，地震灾害频发.本文地震数据发生年份资料中，1962-2010年数据来于《全球地震目录》(宋志平等，2011)，2011-2014年数据源于中国地震信息网(http://www.csi.ac.cn/).ENSO事件资料中，1962-2003年来源于参考文献(李晓燕等，2005)，2004-2012年来源于国家气候中心《ENSO监测简报》21期至53期，且两者资料来源、统计和划分标准基本统一.表 1为1962-2014年斐济群岛及其周边海域所有M_S≥7.1地震.

图 1

Fig. 1

图 1 研究区示意图 Fig. 1 Schematic location of study area

表 1 (Table 1)

表 1 斐济地区1962年以来MS≥7.1地震信息统计表 Table 1 The parameters of earthquake with MS≥7.1 in Fei Ji area 序号 地震时间(年、月、日) 纬度(°S) 经度 深度/km 震级 参考地点 1 1962 4 26 17.873 178.683°W 551.6 7.5 斐济群岛 2 1963 8 25 17.701 178.557°E 570.1 7.1 斐济群岛 3 1969 2 10 22.803 178.795°E 659.9 7.2 斐济群岛南部 4 1970 1 20 25.865 177.173°W 45 7.2 斐济群岛南部 5 1972 3 30 25.725 179.633°E 495.7 7.3 斐济群岛南部 6 1979 11 6 21.09 178.8°W 550 7.7 斐济群岛 7 1980 3 6 18.22 177.83°E 577 7.5 斐济群岛 8 1980 4 13 23.593 177.225°E 148 7.6 斐济群岛南部 9 1984 10 15 15.871 173.554°W 126.2 7.6 斐济群岛北部 10 1986 5 26 20.217 178.953°E 539.8 7.1 斐济群岛南部 11 1990 3 3 21.956 175.171°E 35.5 7.6 斐济群岛西南 12 1992 7 11 22.46 178.36°W 376.3 7.2 斐济群岛南部 13 1994 3 9 17.95 178.417°W 563 7.6 斐济群岛 14 1996 4 16 24.27 176.915°E 100.6 7.2 斐济群岛南部 15 1996 8 5 20.77 178.285°W 550 7.4 斐济群岛东南 16 1998 3 29 17.721 178.971°W 543 7.2 斐济群岛 17 2002 8 19 24.16 178.49°E 699 7.7 斐济群岛南部 18 2004 7 15 17.68 178.52°E 577 7.1 斐济群岛 19 2006 1 2 19.85 177.76°W 594 7.2 斐济群岛 20 2007 12 9 25.996 177.514°E 153 7.8 斐济群岛南部 21 2009 11 9 17.24 178.34°E 590 7.3 斐济群岛 22 2013 5 24 23 177.2°E 160 7.2 斐济以南地区

表 1 斐济地区1962年以来MS≥7.1地震信息统计表 Table 1 The parameters of earthquake with MS≥7.1 in Fei Ji area

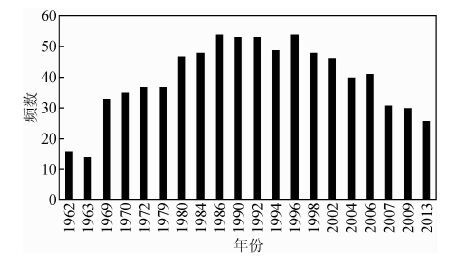
可公度方法是由翁文波先生从天文学引入信息预测学，探讨自然界的秩序(翁文波，1981).“可公度性”作为一种自然界的秩序和规律，它也是对称性规律的一种体现，其对称性既表现在时间上，又表现在空间分布上，具有时空统一性(延军平等，2011).本文采用可公度法对斐济地区M_S≥7.1地震趋势进行判断.

由表 1 知，近53 年来斐济地区发生M_S≥7.1 地震的年份共 22 次，其中1980年和1996年发生两次地震，依据强震群以其主震为代表，同一年份数强震以最大一次为代表，对其可公度性进行分析.因此对20次历史地震进行检验，结果表明: 每一年份都有至少 14 组以上的可公度式子，最高可达到54组可公度式子.由此得出斐济地区M_S≥7.1历史地震有很好的可公度性，如图 2.

图 2

Fig. 2

图 2 三元可公度验证 Fig. 2 The validation of ternary commensurability

设X₁=1962；X₂=1963；X₃=1969；X₄=1970；X₅=1972；X₆=1979；X₇=1980；X₈=1984；X₉=1986；X₁₀=1990；X₁₁=1992；X₁₂=1994；X₁₃=1996；X₁₄=2002；X₁₅=2004；X₁₆=2006；X₁₇=2007；X₁₈=2007，X₁₉=2009，X₂₀=2013，X₂₁=？根据已知年份推算第21次发生地震的可能年份，三元可公度计算方法为：X₂₁=X_m+X_n－X_p.其中m+n-p=21.

三元可公度计算结果为：2014年7组，2015年21组，2016年15组，2017年12组，2018年5组，2019年7组，2020年11组，2021年3组，2022年6组，2023年3组.未来10年中，2015年信号最强，其次为2016年.

采用四元可公度计算.首先计算公差ΔX=Xm+Xn－Xp－Xq, 其中m+n=p+q, X₂₁=X₂₀+ΔX, 统计ΔX出现的频数.

四元可公度计算结果为：2014年128组，2015年117组，2016年89组(表 2).统计得出未来10年中，2014年信号最强，其次为2015年和2016年.

同样，用五元可公度计算，2014年293组，2015年286组，2016年244组(表 2).未来10年中，2014年信号最强，其次为2015年和2016年.

进行可公度计算时主要参考三元可公度计算结果，四元可公度和五元可公度是对三元可公度进行验证.综合三元、四元和五元可公度结果可以得到，未来几年里斐济地区在2015、2016年发生M_S≥7.1地震的信号最强.

表 2 (Table 2)

表 2 斐济地区MS≥7.1地震可公度计算频数 Table 2 The commensurability frequency of earthquake with MS≥7.1 in Fei Ji areas 2014 2015 2016 2017 2018 2019 2020 2021 2022 2023 三元可公度 7 21 15 12 5 7 11 3 6 3 四元可公度 128 117 89 64 58 33 25 7 2 2 五元可公度 293 286 244 196 178 110 73 50 40 14

表 2 斐济地区MS≥7.1地震可公度计算频数 Table 2 The commensurability frequency of earthquake with MS≥7.1 in Fei Ji areas

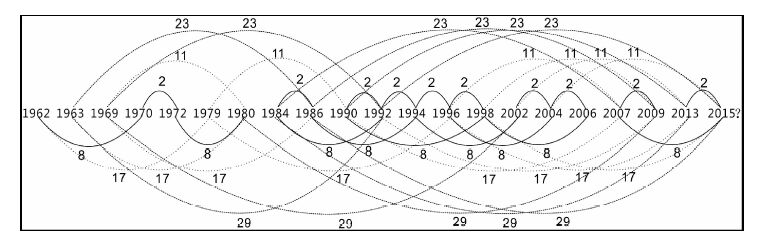
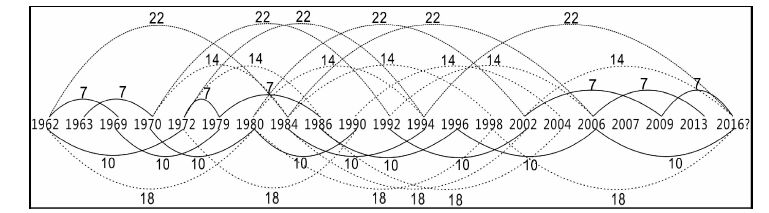
构建斐济地区1962年以来发生M_S≥7.1地震蝴蝶结构图(图 3、图 4)，发现该组数据存在这明显的时间对称性.从中可以看出，与2015年相关的周期有6组，分别为2a、8a、11a、17a、23a、29a；与2016年相关的周期有5组，分别是7a、10a、14a、18a、22a.

图 3

Fig. 3

图 3 斐济地区MS≥7.1强震的2015年预测时间序列蝴蝶结构图 Fig. 3 The butterfly structure diagram of MS≥7.1 earthquakes time series in Fei Ji in 2015

图 4

Fig. 4

图 4 斐济地区MS≥7.1强震的2016年预测时间序列蝴蝶结构图 Fig. 4 The butterfly structure diagram of MS≥7.1 earthquakes time series in Fei Ji in 2016

蝴蝶结构的随机性概率为T=M/N；不漏报置信水平为(1-a)=M/(N+1).其中T为灾害事件时间序列中预测年份发生的可能概率，N为总灾害事件次数，M为参与实际预测的灾害次数，即和主周期关联的年份统计(延军平等，2011).N=20，M₂₀₁₅= 18，M₂₀₁₆=14，2015和2016年斐济地区发生M_S≥7.1地震的随机性概率分别为90％和70％，不漏报置信水平则为 85.7%和66.7%.因此，依据蝴蝶结构图判断2015、2016年斐济地区都有可能发生M_S≥7.1地震，且2015年发生地震的可能性大于2016年.

可公度结构系是自然灾害时间对称性结构的另一种体现，用于表达灾害事件的相互次序和时间韵律特征.从斐济地区M_S≥7.1地震可公度结构系看(图 5)，横向呈现11a、6a的主周期和7a、4a、2a的小周期，纵向呈现10a的主周期和17a、2a、6a年的小周期.该图清晰的反映出斐济地震在时间上具有明显的对称性特征.根据空间平移对称性原理可以推断出2015年、2016年为地震可能发生年，且2015年的可能性高于2016年，这与可公度计算和蝴蝶结构图推断相一致.

图 5

Fig. 5

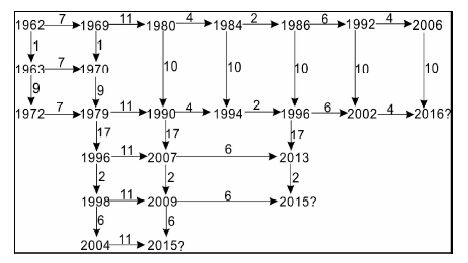
图 5 斐济地区MS≥7.1地震可公度结构系 Fig. 5 Commensurable structure of earthquake (MS≥7.1)in Fei Ji area

对斐济地区及远近海域22次M_S≥7.1地震活动的空间分布特征进行分析(图 6)，对强震发生的震中位置按时间顺序进行空间标注，以3次地震为一期.将相邻三次地震的震中用三角形连起来，共组成7组三角形，发现其具有明显的三角形对称性结构.以180°、21°S为坐标轴，将其分为四个象限，可以看出坐标轴的两侧地震发生次数基本一致.以180°为界，东侧发生9次M_S≥7.1地震，西侧发生13次；以21°S为界，南北区域各发生11次.此外，震中三角形顶点主要分布在第三象限，底边主要分布在一、二象限，呈现西北—东南的对称分布，第7组三角形最后一次地震发生在西北区域，第八组三角形第一次西南区域，预计下一次地震将有两种可能：第一、斐济以南附近小幅迁移，即在 23°S 以南，177°E 以东地区；第二、向东北方向迁移(第二象限).

图 6

Fig. 6

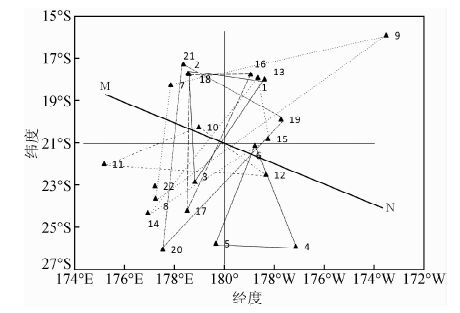
图 6 斐济地区MS≥7.1地震震中对称结构 Fig. 6 The MS≥7.1 earthquake Commensurable structure in Fei Ji area

图 7为斐济地区 M_S≥7.1强震震中经向、纬向迁移示意图.从中可以看出，除个别年份外，震中经向迁移与纬向迁移具有良好的同步性，即当地震震中向东迁移时，纬度上则向北迁移；当震中向西迁移时，纬度上则向南迁移.此外，斐济地震震中对称轴分布在21°S、180°左右，假设斐济地震空间分布具有良好的对称性，那么下次M_S≥7.1地震将可能朝东北方向迁移，即180°以东、21°S以北地区.

图 7

Fig. 7

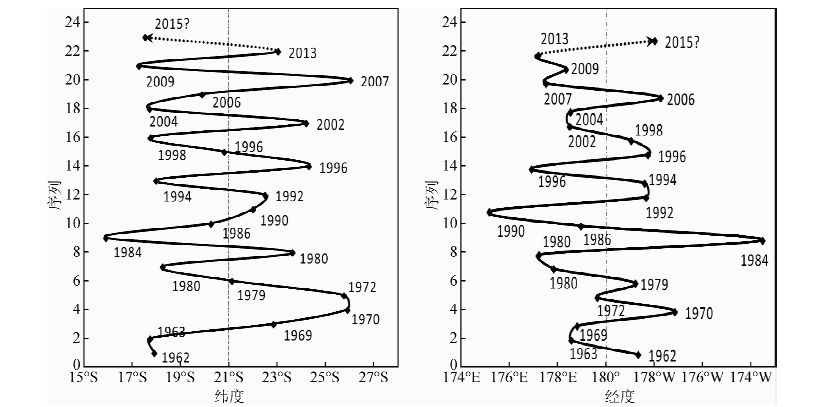
图 7 斐济地区MS≥7.1地震经向、纬向迁移 Fig. 7 The MS≥7.1 earthquake for latitudinal and longitudinal migration in Fei Ji

如果说，当一次强震发生后，巨大的应力释放，引起断层的破裂，影响另一个孕震区的发展，孕育新的强震(郭增建和秦保燕，1983).那么，下次斐济地区强震震中经纬向迁移将有 2 种可能：①在 2013年附近小幅迁移，即在 23°S 以南，177°E以东地区；②沿西南—东北方向直接迁移到第一象限.该结论和上述空间对称性分析的结论一致.

有关数据表明，在过去的几十年中，厄尔尼诺事件的数目有所增加，而拉尼娜事件的数目却在减少(Trenberth and Hoar, 1996).而更多的证据表明厄尔尼诺现象与地震活动性有关(Walker, 1995).D.A. Walker 曾对南太平洋地区地震和厄尔尼诺现象进行相关分析，得出强烈的地震活动和厄尔尼诺在时间上有很好的对应关系.本文通过对ENSO事件和斐济地区地震两者的发生时间进行对比分析(图 8)，发现两者存在较好的对应关系，绝大多数地震都发生在正常年份和厄尔尼诺年，而拉尼娜年份地震发生频率低.自1962年以来发生13次厄尔尼诺现象，仅4次厄尔尼诺期没有发生M_S≥7.1地震.根据2014年11月1日国家气候中心第53期《ENSO监测简报》报道，今年5月又一次新的厄尔尼诺事件已形成，因此对斐济地区地震研究具有重要意义.

图 8

Fig. 8

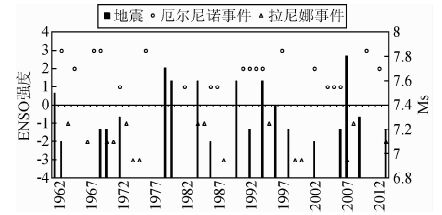
图 8 1962-2013年ENSO事件与斐济地区地震时间对应关系 Fig. 8 The corresponding relationship of time between ENSO and earthquake of Fei Ji area during 1962-2013

对比分析，将22次地震活动年份按ENSO时间进行统计(图 9)，其中厄尔尼诺年份发生10次地震，正常年份发生9次地震，拉尼娜年份发生3次地震，其中1972年、1992年、2004年非常接近厄尔尼诺年份，所以将其归为厄尔尼诺期.根据扇形统计图(图 9)，得到地震在厄尔尼诺年发生的概率为45%，正常年份发生概率为41%，拉尼娜年份概率仅占14%.数据表明斐济地区的强地震与ENSO事件密切相关，也就是说厄尔尼诺年份为斐济地区地震灾害的相对活跃期，而拉尼娜年份是地震发生的相对平静期.

图 9

Fig. 9

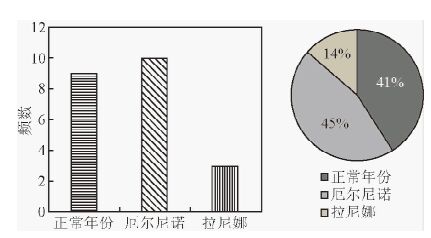
图 9 1962-2014年斐济地区发生MS≥7.1地震数量和频率 Fig. 9 The number and frequency of earthquake of Fei Ji area during 1962-2014

本文运用可公度理论对斐济地区1962年以来M_S≥7.1地震的时空对称性进行分析.此外，根据ENSO事件与斐济地震的相关性，对斐济地区地震发生的机理进行简单探讨，得到结论如下：

(1)运用对称性及可公度法的三元、四元、五元可公度计算分析得出，斐济地区2015年或2016年左可能发生M_S≥7.1地震，且2015年的信号强于2016年.

(2)构建蝴蝶结构图和可公度结构系得出，2015、2016年斐济地区发生M_S≥7.1地震的随机性概率为90%和70%，不漏报置信水平为 85.7%和66.7%.可公度法与蝴蝶结构图法分析得出的结论表现出高度的一致性.

(3)斐济地区M_S≥7.1地震具有良好的空间对称结构，纬向迁移对称轴在21°S左右；经向震中迁移，其对称轴在180°左右，对称中心位于斐济群岛的东南部，呈现西北-东南走向，未来强震震中可能向东北方向迁移，即180°以东、21°S以北地区.

(4)斐济地区M_S≥7.1地震与ENSO事件发生时间存在良好的对应关系.地震主要发生正常年份和厄尔尼诺年份，且厄尔尼诺年份发生率高于正常年份，拉尼娜年份是斐济地区地震发生的相对平静期.

地震预测一直是研究界的难题，为了最大程度地减少自然灾害的损失，在人类越来越失去对自然灾害敏感的情况下，不断探索自然灾害的发生规律就显得非常重要.本文在统计研究的基础上运用可公度理论，对未来斐济地区M_S≥7.1地震进行趋势判断.但由于自然灾害的可公度性是从一些随机事件中提取并非偶然的信号，是一种灾害趋势的研究方法，受各种因素的影响使它的适应性具有一定的区域性，因此仍需继续完善.

致 谢 感谢丁彩霞、刘永林、曹永旺、王璐璐等同事在本文撰写过程中细心的指导，感谢各位审稿老师给予的宝贵意见.