2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
岩体动力反应在很大程度上受到结构面的制约,因此研究结构面的动力特性、特别是动力剪切特性是进行岩体动力反应分析的重要前提(祁生文等,2007).地震荷载既是动荷载也是循环荷载(刘博等,2011),对于静力条件下稳定的岩质边坡,在地震荷载的动态循环剪切作用下,结构面强度降低,导致坡体沿结构面发生错动或滑移,进而引发地质灾害.因此,岩体结构面在动态循环剪切荷载作用下的强度劣化及变形机制是进行工程地震防控工作中亟待解决的关键科学问题之一.
岩体力学行为的室内试验研究是构建岩体本构模型和进行工程设计数值模拟的前提和依据,因此进行岩体结构面动态循环剪切室内试验,即在一定法向应力控制下对岩体结构面试样施加不同剪切变形速率的循环剪切荷载是解决前述问题的重要方法和途径.由于受到仪器设备的限制,前人的研究工作主要集中在循环剪切荷载作用下岩体结构面力学特性方面.例如Plesha(1987),Hutson和Dowding(1990),Jing等(1993),Huang等(1993),Qiu等(1993),Hom and等(2001),Lee等(2001),Jafari等(2003),刘博等(2011,2013)研究了天然岩体结构面(或人工岩体结构面)在循环荷载作用下的剪切力学行为,而在不同剪切速率下岩体结构面动态剪切强度特性方面的研究工作较少.本文总结了国内外能用于测试岩体结构面动态剪切强度特性的直剪试验仪和相关室内试验研究现状,分析了结构面物理力学性质、剪切加载 路径、法向应力、剪切速率、初始起伏度和粗糙度、循环剪切次数等因素对岩体结构面动态剪切强度特性的影响,提出了岩体结构面动态剪切强度特性研究的不足,展望了研究趋势.
1 室内直剪试验仪岩体结构面室内直剪试验仪是进行岩体结构面剪切行为测试的主要设备.直剪仪通常包括法向加载装置、水平加载装置、剪切盒、液压控制装置和数据采集处理装置等(Kana et al.,1996;Jiang et al.,2004;Barla et al.,2010).地震荷载对岩体结构面的动态剪切作用概化为不同剪切变形速率条件的岩体结构面动态直剪试验.目前,国内外能用于进行岩体结构面动态剪切试验的直剪仪(下文简称动态直剪仪)较少,如表 1所示,主要原因在于动态直剪仪需要配备大流量伺服油源并辅以相应容积的蓄能器.
|
|
表 1 典型动态直剪仪指标参数表 Table 1 Index parameters of representative dynamic direct shear apparatus |
岩体结构面抗剪强度特性具有明显的尺寸效应,根据Barton结论,剪切盒内试样最大长度宜为100~1000 mm(Barton and Choubey,1977);根据典型强震记录(胡聿贤,2006;黄润秋,2012),最大剪切速率宜在600~1000 mm/s范围内;根据胡聿贤(2006)结论,最大剪切频率宜在10~20 Hz范围内.分析表 1发现,对于武汉岩土力学研究所、卧龙岗大学(University of Wollongong,Australia)和加泰罗尼亚理工大学(Universitt Politècnica de Catalunya,Spain)的动态直剪仪(如图 1~3所示),其试验样品的尺寸较小,剪切速率较低;对于弗莱贝格工业大学(Technische Universitt Bergakademie Freiberg,Germany)的动态直剪仪(如图 4所示),其剪切速率相对较低;而对于多伦多大学(University of Toronto,Canada)和约瑟夫傅里叶大学(Université Joseph Fourier,France)的动态直剪仪(如图 5~6所示),其试验样品的尺寸相对较小.
 | 图 1 武汉岩土力学研究所直剪仪 Fig. 1 Dynamic direct shear apparatus of Institute of Rock and Soil Mechanics,Chinese Academy of Sciences |
 | 图 2 卧龙岗大学动态直剪仪(Indraratna et al.,1998) Fig. 2 Dynamic direct shear apparatus of University of Wollongong,Australia(Indraratna et al.,1998) |
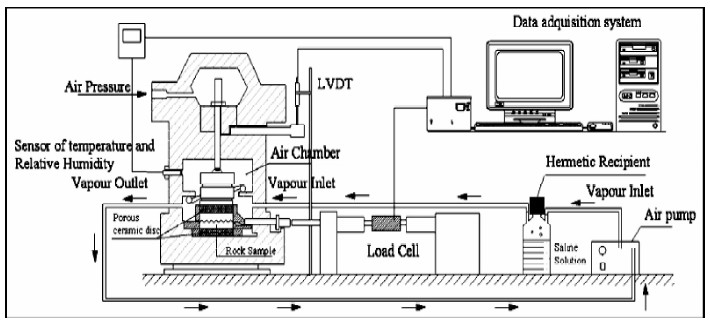 | 图 3 加泰罗尼亚理工大学动态直剪仪(Zand arin et al.,2013) Fig. 3 Dynamic direct shear apparatus of Universitāt Politècnica de Catalunya,Spain(Zand arin et al.,2013) |
 | 图 4 弗莱贝格工业大学动态直剪仪(Konietzky et al.,2012) Fig. 4 Dynamic direct shear apparatus of Technische Universität Bergakademie Freiberg,Germany(Konietzky et al.,2012) |
 | 图 5 多伦多大学动态直剪仪(Crawford and Curran,1981) Fig. 5 Dynamic direct shear apparatus of University of Toronto,Canada(Crawford and Curran,1981) |
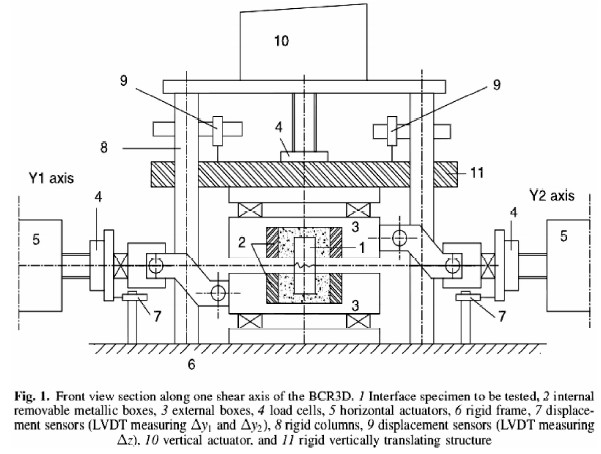 | 图 6 约瑟夫傅里叶大学动态直剪仪(Buzzi et al.,2008) Fig. 6 Dynamic direct shear apparatus of Université Joseph Fourier,France(Buzzi et al.,2008) |
岩体结构面动态剪切室内试验以直剪试验为主,以常规三轴试验为辅.目前的直剪试验方法按剪切位移控制方式可分为斜线段加载试验、三角波形加载试验、正弦波形加载试验、随机波形加载试验,其中斜线段加载试验为单向定速率剪切试验,三角波形加载试验为单向定速率循环剪切或双向定速率循环剪切试验,正弦波形加载试验为单向变速率循环剪切或双向变速率循环剪切试验,随机波形加载试验包括地震波形加载试验等(如图 7所示);按法向荷载控制方式可分为定法向力(Constant Normal Loading)剪切试验和定法向刚度(Constant Normal Stiffness)剪切试验(如图 8所示).由于定法向力条件斜线段加载试验和三角波形加载试验对直剪仪的性能要求较低且容易实施,所以岩体结构面动态剪切强度特性的直剪试验相关成果主要来自上述两种试验加载方式;定法向刚度剪切试验主要适用于起伏岩体结构面.对于结构面试样,人工岩体结构面试样相比于天然岩体结构面试样制样方便,结构面初始起伏度和粗糙度(夏才初,1996)可控,可进行大量平行试验以探究单因素变量或多因素变量对结构面动态剪切强度特性的影响.
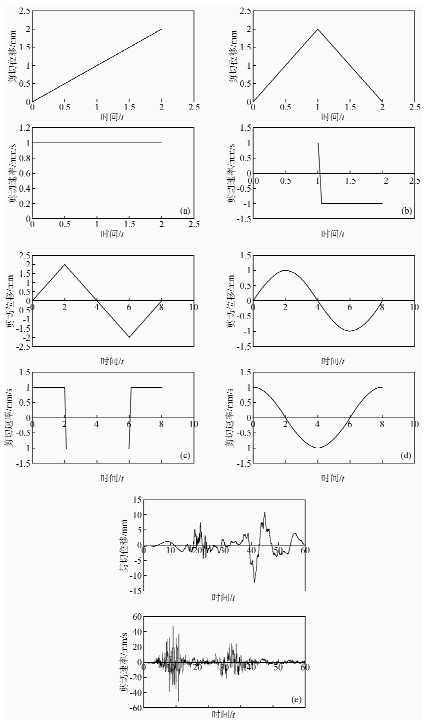 | 图 7 按剪切位移控制方式的剪切加载路径图 Fig. 7 Shear loading path under the control of shear displacement |
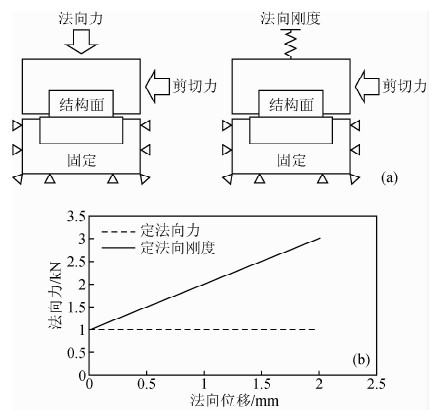 | 图 8 按法向荷载控制方式的剪切加载路径图 Fig. 8 Shear loading path under the control of normal load |
Dieterich(1978)认为不同的剪切速率对岩体结构面的磨损程度产生不同影响,进而影响结构面的滑动摩擦系数,并根据Dieterich(1972)花岗岩直剪试验结果和Scholz和Engelder(1976)关于金刚砂在不同岩石表面的滑动试验结果提出,当剪切速率在0~0.1 mm/s范围内时,滑动摩擦系数满足公式(1),表达式为
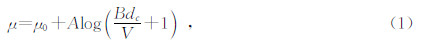
李海波等(2006)通过武汉岩土力学研究所RMT-150C岩石力学试验系统对规则锯齿型水泥结构面试样(见图 9)进行不同法向应力不同剪切速率下的直剪试验,试样尺寸长×宽为150×150 mm(如表 2所示).
 | 图 9 锯齿型水泥结构面试样图(李海波等,2006) Fig. 9 Specimen of cement joint of saw-tooth(Li et al.,2006) |
|
|
表 2 水泥结构面试样试验参数表(李海波等,2006) Table 2 Experiment parameters of cement joint specimen(Li et al.,2006) |
试验结果表明:水泥结构面峰值抗剪强度随法向应力的增大而线性增大;水泥结构面峰值抗剪强度随结构面初始起伏角度的增大而增大,且增大幅度随起伏角度的增大而减小;水泥结构面峰值抗剪强度随剪切速率的增大而减小,且减小幅度随剪切速率的增大而减小.基于试验结果,作者提出了岩体结构面峰值抗剪强度公式,表达式为
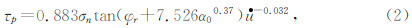
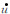 为剪切速率.公式(2)表明结构面抗剪强度随剪切速率的增大而呈指数减小趋势,随初始起伏角度的增大而呈指数增大规律.
为剪切速率.公式(2)表明结构面抗剪强度随剪切速率的增大而呈指数减小趋势,随初始起伏角度的增大而呈指数增大规律.
尽管上述公式与试验结果拟合较好,但是该公式未描述不同初始起伏角度的起伏体破坏模式和磨损剪断程度的差异,无法预测天然岩体无规则起伏结构面的抗剪强度.
2.1.3 Atapour和Moosavi(2013,2014)结构面动态剪切试验Atapour和Moosavi(2013,2014)对平直型石膏结构面试样、平直型混凝土结构面试样和平直型 石膏-混凝土结构面试样进行不同法向应力不同剪切速率的直剪试验(如表 3所示);石膏代表软岩材料,而混凝土代表硬岩材料,石膏-混凝土结构面代表软-硬材料接触面.
|
|
表 3 人工结构面试样试验参数表(Atapour and Moosavi,2013,2014) Table 3 Experiment parameters of artificial joint specimen(Atapour and Moosavi,2013,2014) |
对于石膏结构面而言,试验结果发现:(1) 峰值抗剪强度随法向应力的增大而线性增大,且增大幅度随剪切速率的增大而呈减小趋势;(2) 峰值抗剪强度随剪切速率的增大而减小,且减小幅度随法向应力的增大而呈增大趋势;(3) 总摩擦角随剪切速率的增大而减小;(4) 剪切刚度随法向应力的增大而增大,与剪切速率的负对数呈线性关系,随剪切速率的增大而显著减小,且减小幅度随剪切速率的增大而减小.
对于混凝土结构面而言,试验结果发现:(1) 峰值抗剪强度随法向应力的增大而线性增大;(2) 峰值抗剪强度随剪切速率的增大而呈增大趋势,且增大幅度随法向应力的增大而增大;(3) 总摩擦角随剪切速率的增大而增大;(4) 剪切刚度随法向应力的增大而增大,随剪切速率的增大而显著减小,且减小幅度随剪切速率的增大而减小.
对于石膏-混凝土结构面而言,其速率相关的抗剪强度特性与石膏-石膏结构面相似,因此,软岩-硬岩结构面的动态剪切强度特性主要取决于软岩材料.
Atapour和Moosavi认为,在较高法向应力和较低剪切速率下,由于软岩结构面微凸体的“挤压蠕变”特性增强,结构面之间的真实接触面积增多,抗剪作用增强,因此抗剪强度较高;随着法向应力降低和剪切速率升高,微凸体的“挤压蠕变”作用减弱,结构面之间的真实接触面积减少,抗剪能力降低.然而他们并未对硬岩结构面动态剪切强度的率相关特性做出解释说明.
2.2 定法向力条件三角波形加载试验Crawford和Curran(1981)通过多伦多大学动态直剪仪对不同岩性结构面试样进行不同法向应力不同剪切速率下的直剪试验(如表 4所示).
|
|
表 4 天然岩体结构面试样试验参数表(Crawford and Curran,1981) Table 4 Experiment parameters of natural joint specimen(Crawford and Curran,1981) |
rawford和Curran(1981)考虑了结构面微凸体接触时间、接触面积、接触行为、刚度、矿物组成和法向应力等因素的影响,并对试验结果进行了定性分析.试验结果表明:法向应力和剪切速率对结构面的抗剪强度产生显著影响,且速率相关的抗剪强度变化幅度与岩性和法向应力相关,具体表现为:(1) 随着法向应力增大,结构面的抗剪强度增加;(2) 速率相关的抗剪强度变化幅度与结构面力学特性或者矿物组成相关性不显著,但是与结构面壁岩硬度有弱相关性.(3) 当法向应力较低时,如白云岩结构面试样随剪切速率增加,其抗剪强度呈现先增大,后不变的趋势,而当法向应力较高时,其抗剪强度随剪切速率增加先不变后减小;对于如花岗岩的中硬岩结构面试样其抗剪强度的剪切速率相关性不大;而对于如正长 岩和砂岩的硬岩结构面试样的抗剪强度随剪切速率的变化显著.
2.3 定法向力条件正弦波形加载试验(1) Kana等(1996)通过美国圣安东尼奥西南研究所核废料管理分析中心的直剪仪对凝灰岩结构面试样进行正弦波形加载试验,试样尺寸长×宽为203×203 mm,剪切频率为1.4 Hz,剪切位移幅值为12 mm.试验结果表明结构面一级起伏体和二级起伏体(Patton,1966)对结构面动态剪切响应具有重要影响.根据一级起伏体对结构面法向位移-剪切位移曲线和剪切应力-剪切位移滞回曲线的影响,Kana等对“内锁/摩擦”本构模型优化,使得该模型能充分描述结构面的一阶和高阶动态剪切响应.其中,动摩擦系数是剪切应力-剪切位移滞回曲线形状的主要影响因素;高阶动态剪切响应是二级起伏体和直剪仪的共振结果.
(2) Fox等(1998)在Kana工作的基础上利用砂浆结构面试样做了进一步研究,验证了“内锁/摩擦”模型参数与结构面粗糙度和相对匹配度的经验关系.“内锁/摩擦”模型由内锁方程和摩擦方程相加组成,如公式(3)所示,法向位移-剪切位移关系如公式(4)所示,表达式为
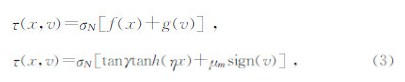

公式(3)(4)中的γ、η、μm、bn是塑造结构面剪切应力-剪切位移滞回曲线和法向位移-剪切位移曲线的四个关键参数,且均能通过测量结构面的粗糙度和相对匹配度来直接得到.因此,“内锁/摩擦”本构方程简单实用.
尽管如此,上述“内锁/摩擦”本构方程只能代表凝灰岩结构面的平均剪切行为,且由于方程中未描述结构面微凸体退化对剪切行为的影响,因此该方程无法完全体现动态循环剪切行为过程.
2.4 定法向刚度条件斜线段加载试验Atapour和Moosavi(2013,2014)对规则锯齿型石膏结构面试样、规则锯齿型混凝土结构面试样和规则锯齿型石膏-混凝土结构面试样进行定法向刚度条件不同初始法向应力不同剪切速率的直剪试验(如表 5所示).
|
|
表 5 人工结构面试样试验参数表(Atapour and Moosavi,2013,2014) Table 5 Experiment parameters of artificial joint specimen(Atapour and Moosavi,2013,2014) |
试验结果表明:对于初始起伏角度为10°的石膏结构面试样,由于受到定法向刚度条件的限制,法向位移-剪切位移的峰值剪胀角小于10°,介于3°~6°范围内,且随剪切速率的增大而增大,剪胀作用引起结构面法向应力增大,进而引起抗剪强度增加;但是,随剪切速率增大而增大的剪胀角引起的抗剪强度增幅小于随剪切速率增大而减小的基本摩擦角导致的抗剪强度降幅,因此初始起伏角度为10°的石膏结构面峰值抗剪强度随剪切速率的增大而呈线性减小趋势.相比于初始起伏角度为10°的石膏结构面试样,相同起伏角度的混凝土结构面试样剪切滑动后表现出更显著的应变硬化行为,原因是石膏结构面起伏体更容易被压碎;随剪切速率的增大峰值剪胀位移和峰值剪胀角呈减小趋势,但减小幅度小于石膏结构面的峰值剪胀位移和峰值剪胀角随剪切速率的增大趋势;随剪切速率的增大剪切刚度减小,且降幅随剪切速率的增大而减小;随剪切速率的增大峰值抗剪强度减小,由此可知随剪切速率增大而减小的剪胀角导致的抗剪强度降幅大于随剪切速率增大而增大的摩擦角引起的抗剪强度增幅.
对于初始起伏角度为20°的石膏结构面试样,由于剪胀角随剪切速率的增大而呈减小趋势,加之摩擦角随剪切速率的增大而减少,因此峰值抗剪强度随剪切速率的增大而减小,且降幅大于10°的石膏结构面试样.对于初始起伏角度为20°的混凝土结构面试样,随着剪切速率的增大,峰值剪切位移、峰值膨胀位移和峰值膨胀角增大,加之摩擦角随剪切速率的增大而增大,因此峰值抗剪强度随剪切速率的增大而呈增大趋势,且增幅大于相同起伏角度石膏结构面试样的降幅. 对于初始起伏角度为20°的石膏-混凝土结构面试样,其剪切应力-剪切位移曲线表现出与初始起伏角度为20°石膏结构面试样剪切应力-剪切位移曲线相似的变化趋势和形状,峰值抗剪强度随剪切速率的增大而减小,且降幅小于相同起伏角度石膏结构面试样的降幅,因此,和定法向力条件类似,定法向刚度条件软岩-硬岩结构面的动态剪切行为主要取决于软岩材料.
2.5 定法向刚度条件三角波形加载试验Mirzaghorbanali等(2014)通过卧龙岗大学直剪仪进行定法向刚度条件不同初始法向应力不同剪切速率的直剪试验(如表 6所示).
|
|
表 6 人工结构面试样试验参数表(Mirzaghorbanali et al.,2014) Table 6 Experiment parameters of artificial joint specimen(Mirzaghorbanali et al.,2014) |
试验结果表明:(1)在较低初始法向应力下,剪切应力-剪切位移回滞曲线近似呈中心对称,且相同剪切位移点的正向剪切应力高于反向剪切应力;随着剪切速率的增大抗剪强度减小,随着循环次数的增加抗剪强度减小,且在较高剪切速率下当循环次数达到100时抗剪强度下降45%;(2)在较高初始法向应力下,剪切机制受微凸体的剪断破坏控制;当剪切速率由5 mm/s增加到20 mm/s时抗剪强度下降4%,随着循环次数的增加抗剪强度减小;(3)在中等初始法向应力下,前期循环剪切行为与较低初始法向应力的循环剪切行为相似,后期循环剪切行为与较高初始法向应力的循环剪切行为相似,原因是微凸体的抗剪作用由抗滑机制转变成抗剪断机制;随着初始法向应力增大,抗剪强度的速率相关性减弱;随着剪切速率增大,峰值剪胀角无规律性变化.由于结构面试样材料、结构面起伏度和法向刚度值单一,加之未考虑尺寸效应的影响,上述结论具有很大的局限性,且未形成定法向刚度条件的结构面动态循环剪切定量关系式.
2.6 常规三轴试验Jafari等(2003)对圆柱状60°贯通规则锯齿型砂浆结构面试样进行了0.05~0.4 mm/min范围内不同轴向加载速率的常规三轴加载试验和循环加卸载试验(见图 10).试验结果表明:当围压为4 MPa时,随着剪切速率的增加结构面峰值抗剪强度降低,且剪切应力-剪切位移曲线由脆性向塑性转变,而在较高剪切速率下,峰值抗剪强度与残余抗剪强度接近相同.由于剪切位移受限,上述试验结果可能与结构面的二级起伏体有关.基于试验结果,Jafari等提出了较低循环剪应力下的峰值抗剪强度预测公式,如公式(5)所示.
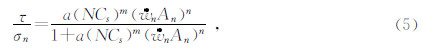
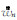 为归一化的剪切速率;An为归一化的循环剪应力;a为与结构面力学特性和几何特性有关的参数;m为与循环剪切次数有关的参数;n为与剪切速率和循环剪应力有关的参数.不难发现,该预测公式缺乏明确的物理意义,且能否适用于较高速率范围的天然岩体结构面动态剪切强度评价需要进一步的验证.
为归一化的剪切速率;An为归一化的循环剪应力;a为与结构面力学特性和几何特性有关的参数;m为与循环剪切次数有关的参数;n为与剪切速率和循环剪应力有关的参数.不难发现,该预测公式缺乏明确的物理意义,且能否适用于较高速率范围的天然岩体结构面动态剪切强度评价需要进一步的验证.
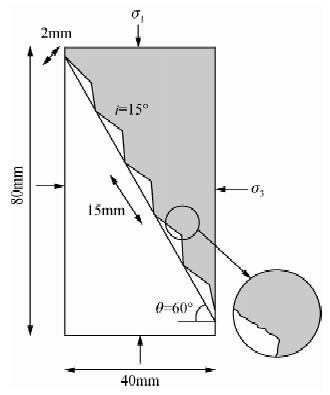 | 图 10 圆柱状锯齿型砂浆结构面试样图 (Jafari et al.,2003) Fig. 10 Cylindrical specimen of motar joint of saw-tooth(Jafari et al.,2003) |
本文针对岩体结构面动态剪切问题,总结了国内外能用于测试岩体结构面动态剪切强度特性的室内直剪仪和相关的室内试验研究现状.前人研究发现影响岩体结构面动态剪切强度特性的因素包括结构面物理力学性质、剪切加载路径、法向应力、剪切速率、初始起伏度和粗糙度、循环剪切次数等.对于定速率剪切试验,在较低剪切速率范围内:
(1) 人工岩体结构面峰值抗剪强度随剪切速率的变化而变化,且变化幅度随法向应力的增大而增大、随初始起伏度的增大而增大、随循环次数的增加而减小.
(2) 人工岩体起伏结构面剪胀位移曲线和峰值剪胀角随剪切速率的变化而变化.
(3) 对于较软的人工岩体结构面峰值抗剪强度随剪切速率的增大而减小,较硬的人工岩体结构面峰值抗剪强度随剪切速率的增大而增大;对于软硬互层的人工岩体结构面的动态剪切强度特性主要取决于较软结构面的动态剪切行为.
(4) 对于均质性和各向同性较强的天然岩体结构面峰值抗剪强度随剪切速率的增大而减小,对于非均质性和各向异性较强的天然岩体结构面峰值抗剪强度随剪切速率的增大而增大.在较高速率范围内天然岩体结构面的抗剪强度特性随剪切速率变化复杂.
剪切速率对结构面抗剪强度的影响主要体现在不同剪切速率对初始起伏体和微凸体的影响不同,导致结构面间的抗剪机制发生变化,因而产生不同的本构规律;随着剪切行为的进行,结构面壁岩磨损或剪断形成的颗粒物质夹杂在结构面之间产生“滚动摩擦”效应,使得结构面的抗剪机制更加复杂.
目前国内外能用于测试岩体结构面动态剪切强度特性的仪器不多,且仪器指标参数如剪切速率、法向应力加载条件以及试样尺寸变化范围等无法完全满足相关试验要求.由于受到仪器设备的限制,诸如剪切速率、法向应力、初始起伏度和粗糙度、循环剪切次数等影响岩体结构面动态剪切强度特性的因素变化幅值较小,因此所得结论具有很大的局限性.岩体结构面尺寸效应和壁岩强度对速率相关的岩体结构面抗剪强度影响的试验成果缺乏.另一方面,目前岩体结构面动态剪切试验数据主要来自规则起伏的人工岩体结构面,天然岩体结构面试验数据较少;目前岩体结构面正弦波形剪切加载试验数据很少,且未见随机波形加载试验数据和定法向刚度条件下的变速率剪切试验成果.
因此,岩体结构面动态剪切强度的测试装置成为认识结构面动态剪切特性的瓶颈,还亟待加强.我们认为研发新的岩体结构面动态剪切强度特性测试的室内试验系统,使得剪切速率、法向应力、初始起伏度和粗糙度、循环剪切次数等具有足够大变化范围,同时辅以结构面三维扫描和剪切行为高速摄像的高精度测量装置,扩大岩体结构面动态剪切试验的试样范围,丰富剪切加载方式,深入研究不同剪切速率、法向应力、初始起伏度和粗糙度、结构面壁岩强度、循环剪切次数、剪切位移和尺寸效应等单因素或多因素对岩体结构面动态剪切强度特性的影响,提出普适的抗剪强度经验公式和本构方程,并最终形成岩体结构面动态直剪方法的国际标准,是未来岩体结构面动态剪切问题研究的必由之路.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [1] | Atapour H, Moosavi M. 2013. Some Effects of shearing velocity on the shear stress-deformation behaviour of hard-soft artificial material interfaces[J]. Geotechnical and Geological Engineering, 31(5): 1603-1615, doi: 10.1007/s10706-013-9687-6. |
| [2] | Atapour H, Moosavi M. 2014. The Influence of Shearing Velocity on Shear Behavior of Artificial Joints[J]. Rock Mechanics and Rock Engineering, 47(5): 1745-1761, doi: 10.1007/s00603-013-0481-9. |
| [3] | Barla G, Barla M, Martinotti ME. 2010. Development of a new direct shear testing apparatus[J]. Rock Mechanics and Rock Engineering, 43(1): 117-122, doi: 10.1007/s00603-009-0041-5. |
| [4] | Barton N, Choubey V. 1977. The shear strength of rock joints in theory and practice[J]. Rock Mechanics, 10(1-2): 1-54, doi: 10.1007/BF01261801. |
| [5] | Buzzi O, Boulon M, Hervé M, et al. Leaching of rock-concrete interfaces[J]. Rock Mechanics and Rock Engineering, 2008, 41(3): 445-466. |
| [6] | Crawford A M, Curran J H. 1981. The influence of shear velocity on the frictional resistance of rock discontinuities[C]//International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Pergamon, 18(6): 505-515, doi: 10.1016/0148-9062(81)90514-3. |
| [7] | Dieterich J H. 1972. Time-dependent friction in rocks[J]. Journal of Geophysical Research, 77(20): 3690-3697, doi: 10.1029/JB077i020p03690. |
| [8] | Dieterich J H. 1978. Time-dependent friction and the mechanics of stick-slip[J]. Pure and applied geophysics, 116(4-5): 790-806, doi: 10.1007/BF00876539. |
| [9] | Fox D J, Kana D D, Hsiung S M. Influence of interface roughness on dynamic shear behavior in jointed rock[J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(7): 923-940, doi: 10.1016/S0148-9062(98)00153-3. |
| [10] | Hans J, Boulon M. 2003. A new device for investigating the hydro‐mechanical properties of rock joints[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 27(6): 513-548, doi: 10.1002/nag.285. |
| [11] | Homand F, Belem T, Souley M. 2001. Friction and degradation of rock joint surfaces under shear loads[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 25(10): 973-999, doi: 10.1002/nag.163. |
| [12] | Hu Y X. 2006. Earthquake Engineering[M]. Beijing: Earthquake Press. |
| [13] | Huang R Q. 2012. Engineering Geology for High Rock Slopes[M]. Beijing: Science Press. |
| [14] | Huang X, Haimson B C, Plesha M E, et al. 1993. An investigation of the mechanics of rock joints—Part I. Laboratory investigation[C]// International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Pergamon, 30(3): 257-269, doi: 10.1016/0148-9062(93)92729-A. |
| [15] | Hutson R W, Dowding C H. 1990. Joint asperity degradation during cyclic shear[C]//International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Pergamon, 27(2): 109-119, doi: 10.1016/0148-9062(90)94859-R. |
| [16] | Indraratna B, Haque A, Aziz N. 1998. Laboratory modelling of shear behaviour of soft joints under constant normal stiffness conditions[J]. Geotechnical & Geological Engineering, 16(1): 17-44, doi: 10.1023/A:1008880112926. |
| [17] | Jafari M K, Amini Hosseini K, Pellet F, et al. 2003. Evaluation of shear strength of rock joints subjected to cyclic loading[J]. Soil Dynamics and Earthquake Engineering, 23(7): 619-630, doi: 10.1016/S0267-7261(03)00063-0. |
| [18] | Jiang Y, Xiao J, Tanabashi Y, et al. 2004. Development of an automated servo-controlled direct shear apparatus applying a constant normal stiffness condition[J]. International Journal of Rock Mechanics and Mining Sciences, 41(2): 275-286, doi: 10.1016/j.ijrmms.2003.08.004. |
| [19] | Jing L, Nordlund E, Stephansson O. 1992. An experimental study on the anisotropy and stress-dependency of the strength and deformability of rock joints[C]//International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Pergamon, 29(6): 535-542, doi: 10.1016/0148-9062(92)91611-8. |
| [20] | Jing L, Stephansson O, Nordlund E. 1993. Study of rock joints under cyclic loading conditions[J]. Rock Mechanics and Rock Engineering, 26(3): 215-232, doi: 10.1007/BF01040116. |
| [21] | Kana D D, Fox D J, Hsiung S M. 1996. Interlock/friction model for dynamic shear response in natural jointed rock[C]//International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Pergamon, 33(4): 371-386, doi: 10.1016/0148-9062(95)00073-9. |
| [22] | Konietzky H, Frühwirt T, Luge H. 2012. A new large dynamic rockmechanical direct shear box device[J]. Rock Mechanics and Rock Engineering, 45(3): 427-432, doi: 10.1007/s00603-011-0214-x. |
| [23] | Lee H S, Park Y J, Cho T F, et al. 2001. Influence of asperity degradation on the mechanical behavior of rough rock joints under cyclic shear loading[J]. International Journal of Rock Mechanics and Mining Sciences, 38(7): 967-980, doi: 10.1016/S1365-1609(01)00060-0. |
| [24] | Li H B, Feng H P, Liu Bo. 2006. Study on strength behaviors of rock joints under different shearing deformation velocities[J]. Chinese Journal of Rock Mechanics and Engineering, 25(12): 2435-2440. |
| [25] | Liu B, Li H B, Liu Y Q. 2013. Experimental study of deformation behavior of rock joints under cyclic shear loading[J]. Rock and Soil Mechanics, 34(9): 2475-2488. |
| [26] | Liu B, Li H B, Zhu X M. 2011. Experiment simulation study of strength degradation of rock joints under cyclic shear loading[J]. Chinese Journal of Rock Mechanics and Engineering, 30(10): 2033-2039. |
| [27] | Mirzaghorbanali A, Nemcik J, Aziz N. 2014. Effects of shear rate on cyclic loading shear behaviour of rock joints under constant normal stiffness conditions[J]. Rock Mechanics and Rock Engineering, 47(5): 1931-1938, doi: 10.1007/s00603-013-0453-0. |
| [28] | Patton F D. 1966. Multiple modes of shear failure in rock and related materials. [D] [Ph. D. Thesis]. Department of Geology, University of IIIinois, 282. |
| [29] | Plesha M E. 1987. Constitutive models for rock discontinuities with dilatancy and surface degradation[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 11(4): 345-362, doi: 10.1002/nag.1610110404. |
| [30] | Qi S W, Wu F Q, Yan F Z, et al. 2007. Rock Slope Dynamic Response Analysis[M]. Beijing: Science Press. |
| [31] | Qiu X, Plesha M E, Huang X, et al. 1993. An investigation of the mechanics of rock joints—Part II. Analytical investigation[C]//International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Pergamon, 30(3): 271-287, doi: 10.1016/0148-9062(93)92730-E. |
| [32] | Scholz C H, Engelder J T. 1976. The role of asperity indentation and ploughing in rock friction—I: Asperity creep and stick-slip[C]//International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Pergamon, 13(5): 149-154, doi: 10.1016/0148-9062(76)90819-6. |
| [33] | Xia C C. 1996. Study of surface morphology of rock joints[J]. Journal of Engineering Geology, 4(3): 71-78. |
| [34] | Zandarin M T, Alonso E, Olivella S. 2013. A constitutive law for rock joints considering the effects of suction and roughness on strength parameters[J]. International Journal of Rock Mechanics and Mining Sciences, 60: 333-344, doi: 10.1016/j.ijrmms.2012.12.007. |
| [35] | 胡聿贤. 2006. 地震工程学[M]. 北京: 地震出版社. |
| [36] | 黄润秋. 2012. 岩石高边坡稳定性工程地质分析[M]. 北京: 科学出版社. |
| [37] | 李海波, 冯海鹏, 刘博. 2006. 不同剪切速率下岩石节理的强度特性研究[J]. 岩石力学与工程学报, 25(12): 2435-2440. |
| [38] | 刘博, 李海波, 朱小明. 2011. 循环剪切荷载作用下岩石节理强度劣化规律试验模拟研究[J]. 岩石力学与工程学报, 30(10): 2033-2039. |
| [39] | 刘博, 李海波, 刘亚群. 2013. 循环剪切荷载作用下岩石节理变形特性试验研究[J]. 岩土力学, 34(9): 2475-2488. |
| [40] | 祁生文, 伍法权, 严福章, 等. 2007. 岩质边坡动力反应分析[M]. 北京: 科学出版社. |
| [41] | 夏才初. 1996. 岩石结构面的表面形态特征研究[J]. 工程地质学报, 4(3): 71-78. |
 2015, Vol. 30
2015, Vol. 30


