直流电法是以地壳中岩矿石的导电性差异为基础,通过观测与研究人工建立的地下电流场的分布规律进行找矿和解决地质问题的一组电法勘探分支方法(李金铭,2005).然而传统的一维和二维电法勘探随着目标深度增加和地质条件复杂化而体现出一定局限性,已不能满足地质勘探中的越来越高的精度要求,因此在复杂地质条件的地区需要开展三维电法勘探,其结果更加精确,并且有利于成果解释.目前三维电法勘探仍是一个研究中的课题,在方法和应用上还远不如二维电法勘探成熟,主要原因有两个:其一,需要先进的仪器系统来进行大面积的三维数据采集,耗费更多的人力和物力,增加了勘探成本.其二,三维电法正反演方法研究和发展还不够成熟,不适用于大量电法数据计算的需要.以下两个发展趋势可以使三维电法的勘探成本迅速降低并得到广泛应用:一是研发可以多个接收机同时进行数据采集的多通道系统,以提高勘探效率和降低成本;二是计算机硬件和反演软件的发展可以使得大量数据的反演能在较短的时间内完成.
分布式采集方式始于地震勘探行业,经过几十年的发展,目前已经非常成熟,这种分布式的多通道数据采集方式使地震勘探数据量成千上万倍地增加,其数据采集和资料解释自动化的进步也提高了地震勘探的效率和精度.因此,采用类似地震勘探中多通道分布式的数据采集方法,可以大大增加电法勘探中数据采集密度和勘探分辨率,高密度电法正是借鉴了这一采集的思想,并取得了巨大成功(Lamontagne and West,1971; Mufti,1978).
分布式的采集方式在电法勘探中的应用相对较少,不管是采集技术还是配套软件都不成熟,也没能形成统一的技术标准,落后地震勘探行业应用20年左右,但是有快速增长的潜力(Kingman et al.,2007).近年来,随着人们对电法勘探越来越高精度要求,分布式三维电法勘探也越来越受到重视,其主要思想是采用多通道分布式的方式尽可能地记录地下三维立体空间的电场分布信息,然后利用三维正演模拟和反演计算进行资料处理解释,从而提高电法勘探分辨软件率(Pridmore et al.,1981;江玉乐等,2007).
所谓分布式是指采集站无需电缆连接,采用GPS同步方式,自动记录信号,通过后期处理解算发射和接收之间的关系.分布式电法勘探多通道的采集方式主要由一个大型网状部署的分布式采集站组成,不但避免了使用大量电缆而产生的电容耦合问题,而且部署方式灵活,能快速采集数据和消除噪声.传统电法探测方法主要用于浅层的矿产资源勘探,采用具有分布式、全三维、全波形、大功率、大极距和多通道特点的电法探测方法将提供更加丰富的电阻率和极化率信息,将为深部矿产资源探测提供有效支撑.
1 原理与特点1.1 基本原理电法勘探种类繁多,但原理都基本相同,不管是常规式还是分布式、二维还是二维电法勘探,都是利用目标地质体和围岩之间的电性差异,以地下介质的电阻率或极化率为物性参数,首先通过一对发射电极向地下供入稳定电流,在地下均匀半空间建立起电流场,然后通过另一对测量电极进行电位差的的测量,最后观测和研究人工建立的地下电流场的分布规律以达到解决地质问题的目的.
为测定均匀大地的电阻率,通常在地面布置四极装置,即两个发射电极A、B和两个测量电极M、N,当通过发射电极A、B向地下发送电流时,就在地下电阻率为ρ的均匀半空间建立起稳定的电场,通过测量到M、N的电位差(UMN和发射电流IAB的大小就可按照一定的公式求出视电阻率值(图 1).
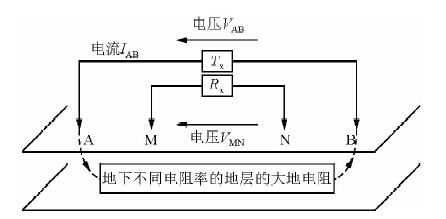 | 图 1 直流电法测量基本原理示意图Fig. 1 The basic principle of DC/IP acquisition |
不同的是,常规二维电法勘探是逐点进行垂向(电测深)或横向(电剖面)的观测,而三维电法是大量电极在平面内进行多通道的观测.三维电法发射和接收电极组合具有多样性,可以同时获取不同区域和不同深度的地电信息.二维电法主要沿测线方向进行测量,反映的是测线方向的二维地电信息,而全三维电法可以获取全空间任意方向丰富的地电信息.
1.2 常规式三维观测系统常规式三维电法观测方式可分为伪三维和真三维观测,如图 2a所示:伪三维观测与二维观测相似,通过布设多条平行的测线,每条测线仅沿测线方向测量,使用软件将这些测线合并拼接,最后将每条测线的测量结果联合起来通过三维反演软件进行反演,这种方式其实是二维采集加上三维反演,只是二维电法的改进,并不是真正的三维观测,它只反映了沿测线方向的电性结构,与测线正交方向的电阻率依然没有体现.真三维观测系统通过网状布设的电极同时对两个正交方向进行供电和测量,通过电极滚动搬家而获得不同区域的地电数据.相比较而言,真三维电法观测方式的结果更为精确,可以获取测线方向和垂直测线方向的电阻率或极化率,但需要较多道数才能获得较大的探测深度,并且其施工困难度和投入成本也较高.
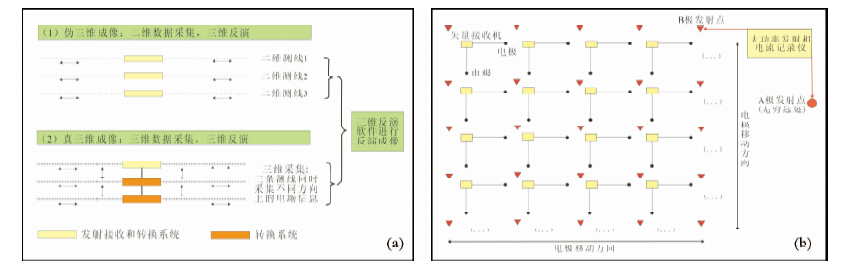 | 图 2 分布式和常规式三维直流电法观测系统示意图
(a)伪3D和真3D电阻率成像示意图;(b)分布式三维观测系统示意图. Fig. 2 Distributed and traditional 3D DC method acquisition configuration(a)Pseudo and true 3D resistivity sketch map;(b)Distributed 3D observation system. |
分布式三维电法采用灵活的电极发射方式和分布式矢量接收方式采集数据,如图 2b所示:将发射极A固定在无穷远处,通过发射极B的移动使发射电极极距和方向发生变化,从而获取不同深度和不同方向的地电信息.接收机在测网中相互独立,以节点的形式分布,每个节点上的接收机布设3个测量电极组成L型,当发射电极与测量电极平行时,可以获得最大强度的信号,正交时获得的信号强度最小.在装置方面也可以根据不同需求采用不同的装置组合,使探测深度和分辨率同时满足要求.该采集方式适合大面积高精度的矿产勘探,不仅可以探测埋深较深的目标体,而且还可以提高横向上的分辨率.
2 仪器系统发展分布式电法仪器系统发展到今天不过30年左右的时间,具有代表性的仪器系统主要有:Anaconda系统、MIMDAS系统、TITAN系统和NEWDAS系统以及法国IRIS公司的分布式系统(Halverson et al.,1979,1989;Halverson,1980; Sheard et al.,1998,2002;White and Gordon,2003;Eaton et al.,2010).这些仪器系统都以一点发射多点接收的形式来采集数据,从概念上来说不同于其它传统的仪器系统,它们都使用了“分布式”的电极排列方式来采集任意道的电法数据.其中,应用比较广泛的是TITAN-24系统和NEWDAS系统.
NEWDAS系统是一个革命性的采集和处理高质量电法数据的系统,它是从Anaconda系统、MIMDAS系统、TITAN系统演变而来,NEWDAS系统主要包含了以下特点:
(1)采用4道24位接收节点;
(2)可进行有线或无线的数据传输;
(3)具有较高的连续采样率;
(4)实时数据监视和分析,每个点都有完整的数据库和用于备份的本地存储空间;
(5)GPS提供排列中的位置和时间信息;
(6)远参考技术和噪声去除方法对数据进行实时校正;
(7)电流可实时监控和反褶积处理;
(8)可使用固定或随机网状发射点来发射电流,通过网状排列的接收点来进行矢量电场测量.
法国IRIS公司的分布式三维数据采集系统包括V-Full Waver电压记录仪和I-Full Waver电流记录仪.V-Full Waver是一个为时间域激发极化、电阻率和自然电位测量所研发的全波形电压记录仪,可以连续记录二次场电压衰减时间序列,同时测量不同方向的电极电位差,测量过程中可存储带有时间戳的全波形数据,经过处理后可以得到视电阻率和视充电率.V-Full Waver主要具有如下几个功能特点:
(1)紧凑性:体积小、功耗低,可以独立自动连续地测量两道全波形时间序列.
(2)灵活性:部署灵活,可以进行高效率的偶极-偶极、梯度、扩展的多极等装置测量,并且还可以进行正交偶极等进一步处理.
(3)远参考技术:通过在距离测区很远的地方放置一个接收机记录参考噪声,进行数值叠加去噪处理,得到高信噪比数据.
(4)内置GPS:提供精准的PPS信号(每秒一个脉冲),用于给全波形时间序列的数据提供时间戳,为工区内所有的接收机提供时间同步的电压波形,通过I-Full Waver在对应时间记录的电流数据可以准确计算出视电阻率和视充电率.
(5)高分辨率:采样率高达100 Hz,通过全波形观测程序可以把多个接收机的数据进行汇总,所有数据都通过GPS-PPS记录的时间信息进行同步,提高了数据性噪比,为深部地质调查或者在强干扰区内提供高质量的数据.
(6)内存大:存储器可以存储2860000个采样数据,相当于8小时采集时间.
3 反演方法及软件发展3.1 三维反演方法电法勘探采集到的数据是不同接收电极在相应位置测量到的电位差计算所得到的视电阻率或视极化率,不能反应地下真实的电性结构,因此还需要对数据进行反演以获得出能反映地下电性结构的真实电阻率和极化率,并以图件的形式直观反映地下地质体的电性变化(严加永等,2012).随着数值计算技术和计算机硬件的发展,国内外关于二维地电场反演研究已比较成熟,三维反演理论方法也发展迅速且日趋成熟,并逐渐广泛应用到生产中.主要方法有原始的最小二乘反演方法,基于Born近似的三维反演,层析成像反演,Tarantola反演,共轭梯度反演,其中很多是三维近似反演方法(吴小平和汪彤彤,2002;黄俊革等,2006).
三维电法反演研究最早始于20世纪90年代初,RSheard(1998)通过电阻率法灵敏度矩阵发现:地质体一般多表现为三维电性结构,对三度体用电剖面数据做二维解释不可避免会有偏差,使三维电法的研究成为该领域的前沿课题(Zhang et al.,1995;Loke and Barker,1996;何继善,1997;Park,1998;庄浩,1998;吴小平和徐果明,2000).Petrick等(1981)使用a中心法对三维电阻率进行反演发现:该方法不仅对初始模型的要求比较高,而且对电导率的变化空间也具有较大限制性要求,因此并未被广泛推广使用;Dines和Lytle(1981)研究了电导率成像方法;Rijo(1984)利用一个简单算法对既定三维模型进行了反演研究,模型的确定性导致该方法未被广泛推广使用;Park和Van Gregory(1991)提出的基于有限差分三维反演算法,宣告三维反演方法系统研究的正式开始;随后几年里Li和Oldenburg(1992,1994)提出了基于Born的近似三维反演,但该方法仅适用于电性结构较为简单的模型,复杂模型计算结果不太准确;Sasaki(1994)详细阐述了基于有限单元法的三维电阻率反演方法,该方法在深部的分辨率低,结果误差较大,其反演速度和精度均没有达到实际应用的要求;Ellis和Oldenburg(1994)系统地论述了三维反演方法;Zhang等(1995)用共轭梯度算法对三维模型进行了正反演研究;Weller等(2000)对三维激电数据进行了反演; Loke(1999)基于二维反演软件RES2DINV,采用强制光滑约束的最小二乘法反演技术开发了三维反演软件RES3DINV;吴小平等(1998),吴小平和徐果明(1999,2000),吴小平和汪彤彤(2002),吴小平(2005)连续多年对三维电阻率成像进行研究,并取得了一些成果;阮百尧和熊彬(2002)针对地下介质的物性变化具有连续性这一特征,提出了三维有限元电阻率测深的数值模拟方法;熊彬等(2003)对复杂条件下的几种典型地质模型的电阻率异常进行了基于四面体单元的三维有限元数值模拟理论研究;黄俊革(2003)提出齐次边界条件、“体积因子”等方法,通过将全局反演改为局部反演来提高反演计算的效率和精度;强建科和罗延钟(2007),强建科等(2010)用三维有限元数值模拟算法分别对起伏地形条件下的电阻率和三维坑道直流聚焦法进行了研究;Revil等(2010)采用了非线性高斯-牛顿算法进行了真三维电阻率成像,将直流电阻率数据和重磁数据联合反演,降低了多解性;Papadopoulos等(2011)提出了一个可以在雅可比矩阵计算前排除冗余参数的三维反演算法,该算法具有快速和高效的特点;刘斌等(2012)基于预条件共轭梯度算法和分解法的特点对三维电阻率反演进行了优化.Qiang等(2013)实现了基于带地形的正则化共轭梯度法的三维直流电阻率反演.戴前伟等(2014)提出了一种基于汉南—奎因信息准则(HQC)的正交最小二乘法(OLS)算法(HQOLS),该方法实现简单,不仅准确性优于BP反演,而且成像质量优于传统最小二乘法.
3.2 三维反演软件目前应用得比较广泛的三维反演软件主要有美国AGI公司的Earthimage3D软件、马来西亚M.H.Loke博士开发的Res3DINV软件、加拿大UBC大学的DCIP3D软件和意大利Geostudi Astier公司的ERTLab64软件.
Earthimage3D是美国AGI公司杨贤进博士开发的可以进行三维电阻率和极化率正反演计算软件,该软件增加了连续电阻率反演、跨孔成像、水下电阻率反演和4D时移反演等功能,拓展了该软件的应用范围.
RES3DINV是马来西亚的M.H.Loke博士于1999年在二维反演软件RES2DINV的基础上,采用基于强制光滑约束最小二乘法反演技术开发的可同时用以电阻率和极化率的三维反演软件,该软件通过采用扭曲的有限元网格模拟表面网格实现地形的校正,无需提供初始模型,像RES2DINV一样完全自动化,对反演结果可以进行任意方向的切片,从而可以形象地刻画电阻率和极化率在地下三维分布情况.
DCIP3D是加拿大UBC大学地球物理方法研究团队GIF中心开发的三维电法软件,该软件基于地质模型的电阻率和极化率的三维属性进行模拟,可用于电阻率和极化率数据的带地形三维正反演,可以处理地面、井中任意位置的不同装置所采集到的电法数据.
ERTLab64是意大利Geostudi Astier公司开发的基于光滑约束的最小二乘法的三维电阻率层析反演软件,其内核采用四面体单元的有限元算法,生成的网格单元质量饱满,能够满足有限元分析计算对网格单元质量的要求,通过预条件共轭梯度法法的引入,使计算效率和精度得到提高.ERTLab64可以对电阻率和极化率进行全三维带地形正演模拟与反演成像,适应于不同装置和不同采集地点(地表、井间、地表与井中)的数据采集工作.
4 应用实例4.1 TITAN-24分布式系统应用实例2007年,Newmont矿业公司在美国Nevada州北部的Brooks勘探区,利用QUANTEC公司的TITAN-24多通道分布式系统进行了二维电阻率、极化率和宽频大地电磁数据的采集(Goldie,2007).数据采集完成后将处理及反演后的结果与常规式三极排列的电阻率、极化率数据进行了对比:图 3a和图 3b分别显示分布式和常规式的视电阻率和视充电率拟断面图,可以看出:分布式与常规式勘探在电阻率数据上有明显的相似性,但是极化率在深部(N>14),数据明显不真实.图 3c和图 3d分别是通过DCIP2D软件反演后的电阻率和充电率结果图,与常规式系统的反演结果相比,分布式系统的电阻率所体现的细节更多,充电率的探测深度更深、分辨率更高.
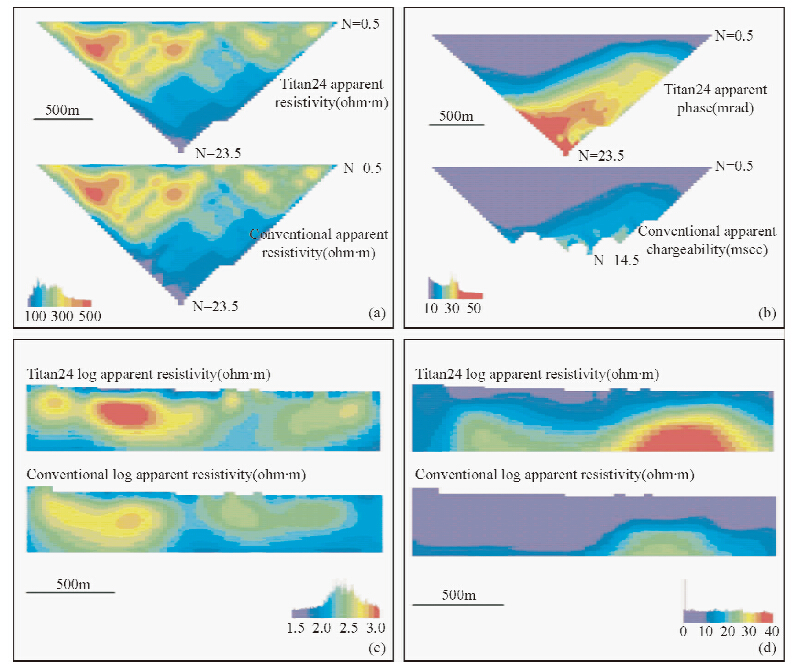 |
图 3 TITAN-24分布式系统应用实例(据Goldie,2007) (a)分布式与常规式视电阻率拟断面对比图;(b)分布式与常规式极化率拟断面对比图;(c)分布式与常规式视电阻率反演结果对比图;(d)分布式与常规式极化率反演结果对比图. Fig. 3 An application of TITAN-24 distributed system(after Goldie,2007) (a)Direct comparison of resistivity pseudosections;(b)Direct comparison of resistivity pseudosections;(c)Comparison of inversion results of resistivity;(d)Comparison of inversion results of IP. |
Newmont公司在Nevada州的实践经验表明:分布式系统不仅在总勘探成本上比常规式系统低,而且能够获得更高质量和更高分辨率的数据,其探测深度是传统方法的两倍. 在该例子中,在不牺牲空间分辨率的前提下,电阻率和充电率探测深度至少是400 m,在过去通常只有小的偶极间距才可以实现.与常规式系统相比,分布采集系统的成本低、效率高,说明分布采集勘探对矿产勘查是一个非常有用的工具.
4.2 NEWDAS三维分布式系统应用实例2010年,Newmont矿业公司又在位于美国Nevada州另一个金矿区利用NEWDAS分布式系统进行了一个小规模三维电法试验.在该试验中,接收点呈网状分布式排列,两道偶极接收电极成L形排列进行矢量测量.一个发射电极固定不动,另一个发射电极在网状结构中以节点的形式移动,这样可以以不同方向和不同发射极距发射电流,试验共进行了539次电流发射,投入了50台接收机布设了300个极距为150 m的相互垂直的偶极接收点(图 4a和图 4b),总共采集了约150000个DC数据点(图 4c),通过数据处理和反演得到了三维电阻率模型(图 4d).该试验以低成本获得了高质量的电法数据,使勘探新区和老区的潜力大大增加,为矿产资源的勘探和评价提供了可供参考的依据.
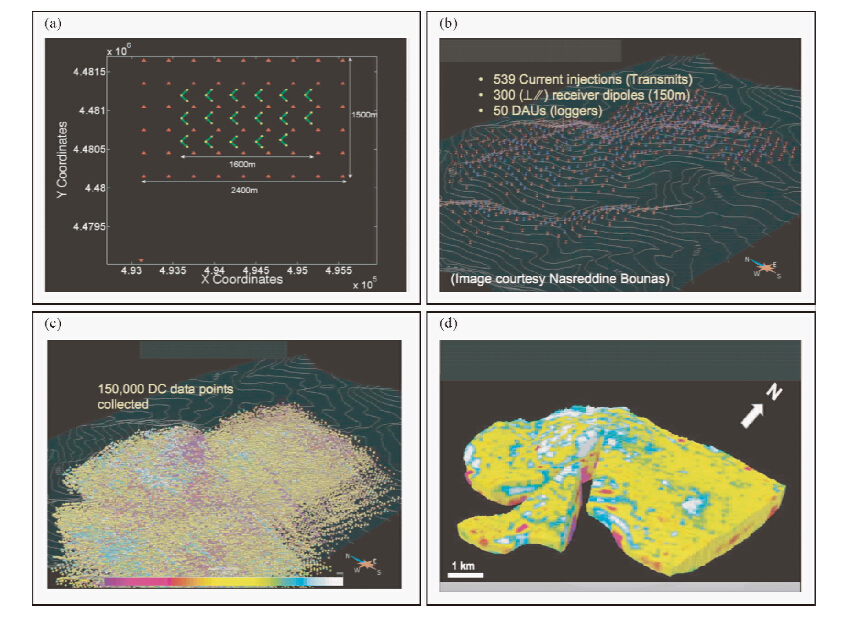 | 图 4 NEWDAS分布式系统应用实例(据 Eaton et al.,2010)
(a)NEWDAS观测系统;(b)电流发射点和偶极接收采集点;(c)采集到直流电法的数据点;(d)三维电阻率模型. Fig. 4 An application of NEWDAS distributed system(after Eaton et al.,2010)(a)NEWDAS distributed acquisition configuration;(b)Current source and receiver dipoles;(c)DC data point collected;(d)3D DC resistivity model. |
2014年5月,作者项目组与恒达新创地球物理公司(北京)、山东地质调查院联合,采用法国IRIS分布式系统在胶东莱州寺庄金矿床开展了相关试验.
4.3.1 矿区地质概况寺庄金矿床大地构造位置位于华北地台之鲁东地盾的胶北隆起西北部,沂沭断裂东侧,南接胶莱拗陷(崔书学和袁文花,2008).金矿床分布于焦家断裂带的南段,以焦家主断裂面为界,东侧为玲珑超单元弱片麻状中粒二长花岗岩,西侧北段为马连庄超单元变辉长岩,南段为玲珑超单元二长花岗岩,中部偏东横贯南北的为绢英岩化花岗岩质碎裂岩,碎裂岩中见有黄铁绢英岩化碎裂岩(图 5).
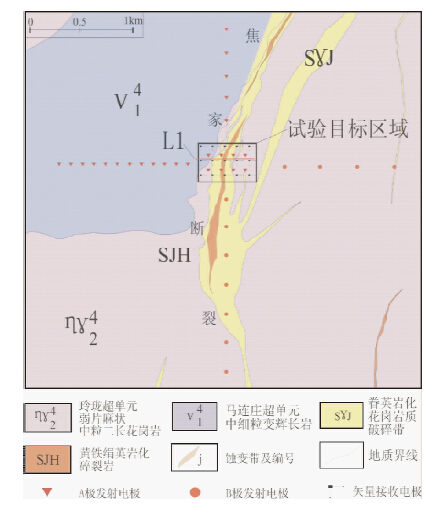 | 图 5 试验区地质简图及观测系统图Fig. 5 Geological map and acquisition system |
区内地层主要为第四系全新统,均为第四系松散堆积物,包括临沂组、沂河组、山前组.岩性为砂质黏土、砂及砂卵石.主要分布于山前坡地、现代河流两侧一级阶地、现代河流的河床及河漫滩.第四系之下,大部分地区为焦家断裂上盘的新太古界变质岩系,有少量的侏罗纪玲珑花岗岩,断裂下盘为侏罗纪玲珑花岗岩(图 6).
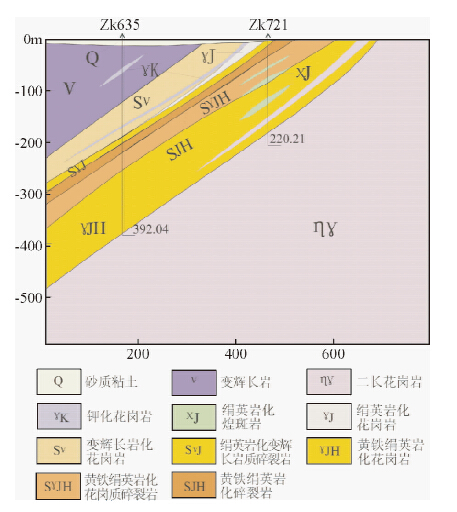 | 图 6 试验区L1线地质剖面图Fig. 6 Geological section of line 1 |
区内构造以脆性断裂为主,矿体的产出主要由焦家主干断裂及其次级断裂控制.区内焦家断裂长4 km左右,宽约80~500 m,延深至1000 m以下,大致走向15°~325°,倾向北西或南西,倾角30°~45°,平面或剖面上呈舒缓波状延伸.断裂主要沿马连庄超单元变辉长岩(原斜长角闪岩)与玲珑超单元二长花岗岩接触带展布,发育有连续稳定的主裂面,上盘从上往下依次为变辉长岩、绢英岩化变辉长岩和绢英岩化变辉长岩质碎裂岩;下盘从上往下依次依次为黄铁绢英岩化碎裂岩、黄铁绢英化花岗岩质碎裂岩、黄铁绢英岩化花岗岩、二长花岗岩(图 6).
矿区岩浆岩广泛分布,以早侏罗纪的玲珑花岗岩为代表,新太古代五台—阜平期马连庄超单元分布于焦家断裂带以西地区.区内脉岩发育,主要分布于玲珑超单元内,主要有伟晶岩、细晶岩、石英闪长岩、闪长玢岩、角闪岩、辉绿玢岩以及煌斑岩脉.马连庄超单元呈岩基状产出,分布于焦家断裂带上盘,并与其下盘的玲珑超单元呈断层接触,其它地段则为侵入接触关系.受焦家主断裂寺庄段的控制,破碎蚀变带形态、规模、产状与断裂带产状基本一致,寺庄以北位于马连庄超单元变辉长岩与玲珑超单元接触带,寺庄以南位于玲珑超单元二长花岗岩中.蚀变带总体形态较稳定,呈舒缓波状延伸,各蚀变岩带之间为渐变过渡关系.
4.3.2 数据采集仪器采用法国IRIS公司的VIP10000大功率电流发射机、全波形矢量接收机V-Full Waver和电流记录仪I-Full Waver.目标区域东西长约900米,南北宽约500米(图 5中矩形区域).为减少施工成本,实现最少的电流发射组合以达到对此类模型的较好分辨率,根据地质和物性资料建立地球物理模型,对合成数据进行不同发射方向、不同发射接收极距的灵敏度、正反演试算分析,最终设计如图 5中所示观测系统:在接收方面,共投入了15台V-Full Waver电压记录仪连接30道15个矢量接收点进行全波形不间断记录,矢量接收点都成网状分布式排列,两道偶极接收电极成L形排列进行矢量测量,接收极距100 m;在发射方面,发射机输出功率10 kW,发射电流为10 A以上,发射时间10分钟左右,共进行了30次电流发射.装置类型采用中梯和三级电测深法的组合形式,投入了1台I-Full Waver电流记录仪进行了全波形不间断记录,共采集了900个DC数据点.
4.3.3 数据处理由于系统采用全波形记录方式,接收电压和发射电流的波形通过GPS时间戳标记,数据处理的时间精度非常高,数据处理流程如下:
(1)数据整理,将测量到的电压和电流文件按照一定规则命名并整理.
(2)数据拾取叠加,首先对自然电位、脉冲滤波和频谱分析,然后挑选采样窗口,按照2 s间隔周期拾取信噪比较高的时段叠加(图 7).
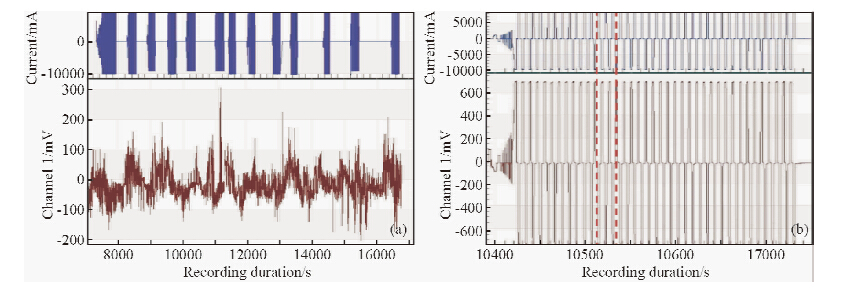 | 图 7 全波形数据采集
(a)多次发射电流信号及其对应的全波形电压信号;(b)单次发射电流信号及其对应电压信号. Fig. 7 Data acquisition of full waveform(a)Multiple transmitter current signal and the corresponding full waveform voltage signal;(b)Single transmitter current signal and the corresponding full voltage signa. |
(3)数据汇总输入,首先将叠加后的输出文件进行汇总,30次发射对应30道数据共计900个数据文件,由于接收机与发射机的时间序列是一一对应的,每次发射电极组合和接收电极都赋予了相应ID,因此我们只需要按照ID将其汇总即可;然后将汇总后的数据点及其ID对应的坐标信息文件结合,进行进一步处理.
(4)剔除坏点,如图 8所示:(a)和(b)分别为Q值和电阻率统计直方图,通过移动红线和蓝线可以设置边界,剔除不合理的值;(c)是加载电极后的电阻率图形剃点模式,通过双击数据点可以剔除出不合理和突变的电阻率值.
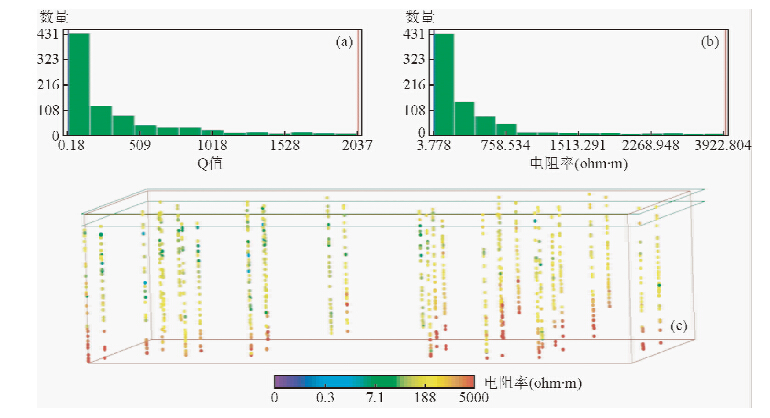 | 图 8 数据预处理示意图
(a)Q值统计直方图;(b)电阻率统计直方图;(c)电阻率图形剃点模式. Fig. 8 Data preprocessing(a)Q-value statistical histogram;(b)Resistivity statistical histogram;(c)The removed point pattern of resistivity. |
(1)地球物理模型建立
根据前人对岩(矿)石电阻率的测定结果(表 1),结合断裂带中矿体产状和矿化类型,进行了适当简化,建立起寺庄矿床三维电阻率模型:模型长900 m,宽500 m,深度1000 m,将地表的第四系覆盖层视为电阻率值为50 Ω·m极低电阻率特征区域;将断裂上盘的变辉长岩视为电阻率值为300 Ω·m的低阻特征区域;将断裂下盘的二长花岗岩视为电阻率值为2000 Ω·m的高阻特征区域;沿上盘和下盘接触带展布的破碎蚀变带过渡区域,由于断裂带非常强烈的构造破碎导致碎裂的岩矿石电阻率下降,岩石经硅化、绢云母化等强烈矿化蚀变作用后电阻率略有回升,因此将其视为电阻率值为1000 Ω·m的中低阻特征区域.
| | 表 1 焦家断裂带岩矿石电性参数表 Table 1 Rock physical property parameters in Jiaojia fault zone |
(2)正反演模拟计算
为了从理论上验证该方法对寺庄金矿床的探测能力,先对该电阻率模型进行正演模拟计算,然后再对正演响应数据进行反演计算,其过程大致如下:
① 对目标区域进行分块并填充相应的电阻率值,建立理论电阻率模型(图 9);
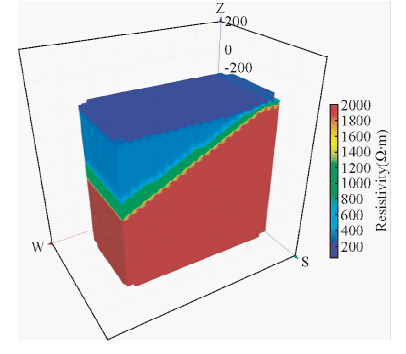 | 图 9 寺庄矿区理论电阻率模型Fig. 9 Theoretical resistivity model in Sizhuang gold field |
② 采用计好的观测系统、采集参数对该模型进行三维有限元正演模拟计算,得到正演响应的视电阻率值;
③ 对正演响应数据模拟实测数据进行反演计算,得到所示三维电阻率模型(图 10).
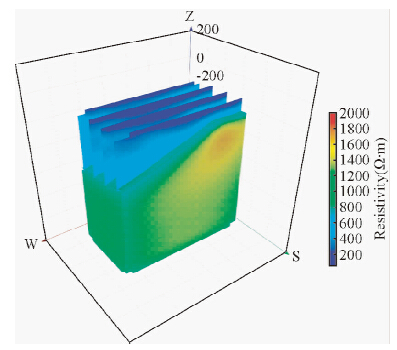 | 图 10 寺庄矿区理论模型正演响应的反演结果Fig. 10 The inversion resistivity model of forward sounding of theory model in Sizhuang gold deposit |
对比图 9和图 10可知:反演得到的电阻率模型很好的反映出了断层上盘变辉长岩和断层下盘二长花岗岩,断裂引起的破碎蚀变带也清晰可见,岩体反映的特征与理论模型和物性资料对应基本一致.因此,基于地质和物性信息分析建立起地球物理模型的正反演研究,不仅证明该观测系统和采集参数的有效性,而且在理论上证明了在焦家式金矿床进行分布式三维电法探测是可行的.
4.3.5 实测数据反演(1)剖分网格
网格剖分大小影响了正反演的精度,细网格可以提高模型网格化转换和计算求解的精度,但是网格剖分过细影响了反演的效率,而且在不同方法和不同模型的反演中,不同网格剖分方式对反演精度的影响也是不同的.综合考虑各方面的因素,并且使反演精度和计算速度都满足要求,先将目标区按50 m×50 m×25 m均匀剖分成若干个平行六面体,再将每个六面体剖分成5个四面体,剖分深度为1000 m(图 11).
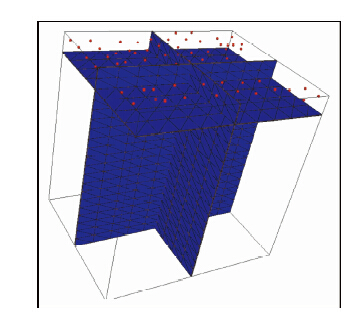 | 图 11 三维网格剖分Fig. 11 3D mesh subdivision |
(2)反演流程
本文采用基于光滑约束的最小二乘的三维反演方法,传统的最小二乘法参数过多会导致反演产生冗余构造,光滑约束的加入使相邻网格间没有突变,使反演求得的模型简单而光滑.反演过程中PCG预条件共轭梯度法的引入,不仅使反演方程的求解具有稳定的优点,而且收敛速度较快.
为不失一般性,使用1000 Ω·m均匀半空间作为反演 的初始模型,标准估计误差值设定为5%,反演深度为1000 m,进行无约束的电阻率反演,PCG内核迭代次数最大为30次,反演过程包括全局反演迭代和PCG预条件共轭梯度内核迭代两个相互嵌套的迭代过程,反演流程如下:
① 建立预测初始三维电阻率模型,采用与背景值接近的1000 Ω·m均匀半空间作为初始模型.
② 正演模拟,基于初始模型进行三维有限元正演模拟得到理论视电阻率(图 12a).
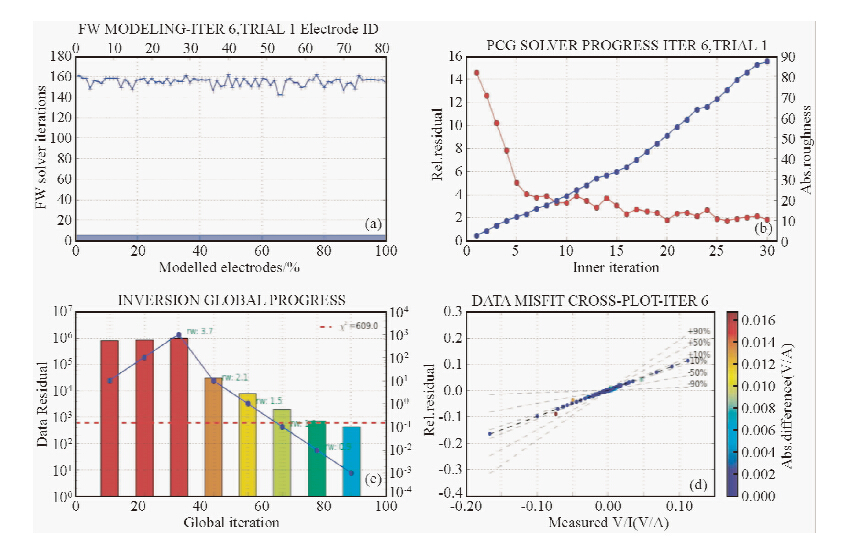 | 图 12 数据反演过程
(a)正演迭代求解;(b)预处理共轭梯度法内部迭代;(c)全局迭代反演;(d)数据拟合差交汇图. Fig. 12 The data inversion progress(a)Forward modeling solver iterations;(b)PCG solver progress;(c)Global iteration inversion progress;(d)Data misfit cross-plot. |
③ 通过最小二乘法构造误差函数计算理论和实际观测视电阻率值的误差,若观测数据和理论值的均方误差不满足收敛条件,进入下一步.
④ 采用PCG内核迭代求解反演方程,若不满足收敛条件,则重新设定PCG初值再次进行内核迭代求解,随着内核迭代次数的增加,残差曲线逐渐减小并趋于平缓,粗糙度逐渐增加;当满足收敛条件时,则得到新模型参数(图 12b).
⑤ 重复步骤②、③和④,将最新求得的模型参数代入有限元正演模拟计算中,开始下一次全局反演迭代,直到理论值和计算值的误差满足收敛时停止全局反演迭代(图 12c和图 12d).
4.3.6 成果综合解释本次反演总共进行了6次全局迭代后反演自动停止,得到三维电阻率模型如图 13所示,根据三条明显的电阻率分界面大致可将其划分为四个电性特征层(图 14):第一层为低阻层,电阻率值大约为0~200 Ω·m,主要分布在大部分地表;第二层为中低阻层,电阻率值变化范围较大,大约200~600 Ω·m,最深处约为400 m,中间部分高阻体向上凸起,部分出露地表,倾向向西,总体展布形态为东浅西深;第 三层为破碎蚀变带,电阻率值变化较小,大约 600~700 Ω·m左右,厚度变化小,大概几十米,层状特征明显,走向大致南北,倾向向西,倾角约为30°~45°,倾角随深度增加逐渐减小;第四层为高阻层,电阻率值大于700 Ω·m,随深度的增加而增加.
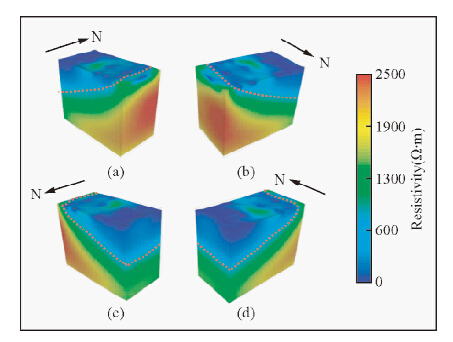 | 图 13 电阻率反演结果
(a)南东向视图;(b)北东向视图;(c)北西向视图;(d)南西向视图. Fig. 13 3D inversion results of resistivity(a)SE view;(b)NE view;(c)NW view;(d)SW view. |
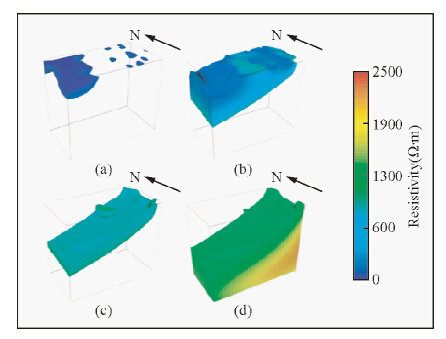 | 图 14 电阻率层位划分
(a)第一层:第四系松散堆积物;(b)第二层:变辉长岩;(c)第三层:破碎蚀变带;(d)第四层:二长花岗岩. Fig. 14 The division layer of resistivity(a)The first layer: Quaternary loose deposits;(b)The second layer: metagabbro;(c)The third layer: the altered fracture zone;(d)The fourth layer: adamellite. |
该试验区域地质构造相对简单,地表主要被第四系松散堆积物所覆盖,与第一层极低电阻率层对应;断层上盘岩性单一,主要为变辉长岩,与电阻率变化较大的第二层对应;断层所控制的破碎蚀变带与第三层对应;断层下盘的二长花岗岩与第四层高阻层所对应.反演结果揭示电阻率由低阻到高阻的接触带和断层控矿带对应良好,倾角基本一致.试验结果表明:随着近年来观测仪器、反演软件的发展,目前分布式三维电法观测已经能适应生产需要,其施工效率高、勘探深度大,能精准的刻画地下目标地质体.
5 结论与展望5.1 通过本次分布式三维直流电法试验,说明该方法具有分辨率高、探测深度大、效率高和成本低等特点,随着近年来观测仪器、反演软件的发展,已基本能满足实际工作的需要,可以在资源勘查、工程和环境监测等领域推广应用. 5.2 采用不间断全波形记录方式的三维分布式电法测量,在干扰严重的老矿区,通过后期的数据处理,仍能挑选到有效的信息,为克服矿区干扰提供了新的可能. 5.3 发射电极之间的切换如果能实现自动化或半自动化,不仅可以增加施工效率,而且可以获得更加丰富的地电信息,是三维直流电法需要改进和发展地方. 5.4 由于布极方式的灵活性,施工地点不应只限于地表,应该朝井间、井-地以及水下发展,并通过注入流体等人为干涉,加上一个时间维,可以应用工程和环境监测等领域. 5.5 三维反演只选择了光滑约束的最小二乘法进行了反演,没有开展多种反演方法的对比工作,以后需要加强这方面的研究工作. 5.6 反演过程中应加入先验地质、构造、岩石物性、钻孔数据和其它地球物理信息进行约束反演以降低反演结果的多解性. 致 谢 在野外试验中得到了恒达新创(北京)地球物理技术有限公司提供的试验设备,刘国庆总经理、阮帅博士、吴肃元、张炯、周志明等工程师在野外数据采集中提供了大力支持,意大利Geostudi Astier 公司Stefano Del Ghi and a到现场进行了数据采集和反演软件指导,山东地调院提供了报告的地质资料,匿名审稿人提出了建设性意见,在此一并表示感谢!| [1] | Cui S X, Yuan W H. 2008. Ore-forming regularity of the second enrichment zone of the Sizhuang gold deposit in Laizhou, Shandong Province[J]. Geological Survey and Research (in Chinese), 31(3):186-191. |
| [2] | Cui Y A, Bai Y C, Du H K. 2005. Data-acquisition instrument design based on extended bus in electromagnetic exploration[J]. Journal of Central South University (Science and Technology), 36(2):288-292. |
| [3] | Dai Q W, Jiang F B, Dong L. 2014. RBFNN inversion for electrical resistivity tomography based on Hannan-Quinn criterion[J]. Chinese J. Geophys. (in Chinese), 57(4):1335-1334, doi:10.6038/cjg20140430. |
| [4] | Dines K A, Lytle R J. 1981. Analysis of electrical conductivity imaging[J]. Geophysics, 46(7):1025-1036. |
| [5] | Eaton P, Anderson B, Queen S, et al. 2010. NEWDAS-the Newmont distributed IP data acquisition system[C].//2010 SEG Annual Meeting. Denver, Colorado:Society of Exploration Geophysicists. |
| [6] | Ellis R G, Oldenburg D W. 1994. The pole-pole 3-D Dc-resistivity inverse problem:a conjugategradient approach[J]. Geophysical Journal International, 119(1):187-194. |
| [7] | Fan C S, Li T L, Yan J Y. 2012. Research and application experiment on 2.5D SIP inversion[J]. Chinese Journal of Geophysics (in Chinese), 55(12):4044-4050,doi:10.6038/j.issn.0001-5733.2012.12.016 |
| [8] | Francese R, Mazzarini F, Bistacchi A, et al. 2009. A structural and geophysical approach to the study of fractured aquifers in the Scansano-Magliano in Toscana Ridge, southern Tuscany, Italy[J]. Hydrogeology Journal, 17(5):1233-1246. |
| [9] | Gharibi M, Killin K, McGill D, et al. 2012. Full 3D acquisition and modelling with the Quantec 3D system-The hidden hill deposit case study[J]. ASEG Extended Abstracts, 2012(1):1-4. |
| [10] | Goldie M. 2007. A comparison between conventional and distributed acquisition induced polarization surveys for gold exploration in Nevada[J]. The Leading Edge, 26(2):180-183. |
| [11] | Halverson M O. 1980. Deep-looking spectral IP using telluric cancellation[C].//presented at the 50th Annual International Meeting and Exposition, SEG. |
| [12] | Halverson M O, Kingman J E E, Corbett J D. 1989. Advances in IP technology:Telluric cancellation and high spatial resolution arrays[C].//Proceedings of Exploration '87:Ontario Geological Survey. Toronto, Ontario, Canada, 183-190. |
| [13] | Halverson M O, Zinn W G, McAlister E D, et al. 1979. Some results of a series of geologically controlled field tests of broadband spectral induced polarization[C].//presented at the 49th Annual International Meeting and Exposition, SEG. |
| [14] | He J S. 1997. Development and prospect of electrical prospecting method[J]. Acta Geophysica Sinica (in Chinese), 40(S1):308-316. |
| [15] | Huang J G. 2003. 3-D resistivity/IP modeling and inversion based on FEM (in Chinese)[D]. Changsha:Central South University. |
| [16] | Huang J G, Wang J L, Ruan B Y. 2006. A study on FEM modeling of anomalies of 3-D high-density E-SCAN resistivity survey[J]. Chinese Journal of Geophysics (in Chinese), 49(4):1206-1214. |
| [17] | Jiang Y L, Kang W F, Zhang N, et al. 2007. Application of high density resistivity method to karst exploration[J]. Journal of Chengdu University of Technology (Science and Technology Edition) (in Chinese), 34(4):452-455. |
| [18] | Kingman J E E, Donohue J G, Ritchie T J. 2007. Distributed acquisition in electrical geophysical systems[C].//Proceedings of the Fifth Decennial International Conference on Mineral Exploration, 425-432. |
| [19] | Kong Q Y, Zhang T Z, Yu X F. 2006. Shandong Deposits[M]. Shandong:Science and Technology Publishing House. |
| [20] | Lamontagne Y, West G F. 1971. EM response of a rectangular thin plate[J]. Geophysics, 36(6):1204-1222. |
| [21] | Li J M. 2005. Geoelectric Field and Electrical Exploration (in Chinese)[M]. Beijing:Geological Publishing House. |
| [22] | Li Y G, Oldenburg D W. 1992. Approximate inverse mappings in DC resistivity problems[J]. Geophysical Journal International, 109(2):343-362. |
| [23] | Li Y G, Oldenburg D W. 1994. Inversion of 3-D DC resistivity data using an approximate inverse mapping[J]. Geophysical Journal International, 116(3):527-537. |
| [24] | Liu B, Li S C, Li S C, et al. 2012. 3D electrical resistivity inversion with least-squares method based on inequality constraint and its computation efficiency optimization[J]. Chinese J. Geophys. (in Chinese), 55(1):260-268, doi:10.6038/j.issn.0001-5733.2012.01.025. |
| [25] | Loke M H, Barker R D. 1996. Practical techniques for 3D resistivity surveys and data inversion[J]. Geophysical Prospecting, 44(3):499-523. |
| [26] | Mufti I R. 1978. A practical approach to finite-difference resistivity modeling[J]. Geophysics, 43(5):930-942. |
| [27] | Pan K J, Tang J T, Hu H L, et al. 2012. Extrapolation cascadic multigrid method for 2.5D direct current resistivity modeling[J]. Chinese J. Geophys. (in Chinese), 55(8):2769-2778, doi:10.6038/j.issn.0001-5733.2012.08.028. |
| [28] | Papadopoulos N G, Yi M J, Kim J H, et al. 2010. Geophysical investigation of tumuli by means of surface 3D electrical resistivity tomography[J]. Journal of Applied Geophysics, 70(3):192-205. |
| [29] | Papadopoulos N G, Tsourlos P, Papazachos C, et al. 2011. An algorithm for fast 3D inversion of surface electrical resistivity tomography data:application on imaging buried antiquities[J]. Geophysical Prospecting, 59(3):557-575. |
| [30] | Park S. 1998. Fluid migration in the vadose zone from 3-D inversion of resistivity monitoring data[J]. Geophysics, 63(1):41-51. |
| [31] | Park S K, Van Gregory P. 1991. Inversion of pole-pole data for 3-D resistivity structure beneath arrays of electrodes[J]. Geophysics, 56(7):951-960. |
| [32] | Petrick W R Jr, Sill W R, Wards S H. 1981. Three-dimensional resistivity inversion using alpha centers[J]. Geophysics, 46(8):1148-1162. |
| [33] | Pridmore D F, Hohmann G W, Ward S H, et al. 1981. An investigation of finite-element modeling for electrical and electromagnetic data in three dimensions[J]. Geophysics, 46(7):1009-1024. |
| [34] | Qiang J K, Han X, Dai S K. 2013. 3D DC resistivity inversion with topography based on regularized conjugate gradient method[J]. International Journal of Geophysics, 2013:Article ID 931876. |
| [35] | Qiang J K, Luo Y Z. 2007. The resistivity FEM numerical modeling on 3-D undulating topography[J]. Chinese Journal of Geophysics (in Chinese), 50(5):1606-1613. |
| [36] | Qiang J K, Ruan B Y, Zhou J J. 2010. Research on the array of electrodes of advanced focus detection with 3D DC resistivity in tunnel[J]. Chinese Journal of Geophysics (in Chinese), 53(3):695-699, doi:10.3969/j.issn.0001-5733.2010.03.024. |
| [37] | Revil A, Johnson T C, Finizola A. 2010. Three-dimensional resistivity tomography of Vulcan's forge, Vulcano Island, southern Italy[J]. Geophysical Research Letters, 37(15). |
| [38] | Rijo L. 1984. Inversion of three-dimensional resistivity and induced-polarization data[C].//54th Ann. Internat. Mtg., Soc. Exp. Geophys., Expanded Abstract. 113-117. |
| [39] | Ruan B Y, Xiong B. 2002. A Finite element modeling of three-dimensional resistivity sounding with continuous conductivity[J]. Chinese Journal of Geophysics (in Chinese), 45(1):131-138. |
| [40] | Sasaki Y. 1994. 3-D resistivity inversion using the finite-element method[J]. Geophysics, 59(12):1839-1848. |
| [41] | Sheard N. 1998. MIMDAS:A new direction in geophysics[C].//Proceedings of the ASEG 13th International Conference. Hobart, Tasmania. |
| [42] | Sheard N, Ritchie T, Rowston P. 1998. MIMDAS - A new direction in geophysics[C].//The 13th International Conference and Exhibition of the Australian Society of Exploration Geophysicists. |
| [43] | Sheard S N, Ritchie T J, Rowston P A. 2002. MIMDAS - A quantum change in surface electrical geophysics[C]. PDAC Conference, Toronto. |
| [44] | Weller A, Frangos W, Seichter M. 2000. Three-dimensional inversion of induced polarization data from simulated waste[J]. Journal of Applied Geophysics, 44(1-2):67-83. |
| [45] | White M, Gordon R. 2003. Deep imaging-New technology lowers cost of discovery[J]. Canadian Mining Journal, 124(3):27-28. |
| [46] | Wu X P. 1998. Study on 3-D resistivity forward and inversion using conjugate gradient method (in Chinese)[D]. Hefei:University of Science and Technology of China. |
| [47] | Wu X P, Xu G M, Li S C. 1998. The calculation of three-dimensional geoelectric field of point source by incomplete cholesky conjugate gradient method[J]. Acta Geophysica Sinica (in Chinese), 41(6):848-855. |
| [48] | Wu X P, Xu G M. 1999. Derivation and analysis of partial derivative matrix in resistivity 3-D inversion[J]. Oil Geophysical Prospecting (in Chinese), 34(4):363-372. |
| [49] | Wu X P, Xu G M. 2000. Study on 3-D resistivity inversion using conjugate gradient method[J]. Chinese Journal of Geophysics (in Chinese), 43(3):420-427. |
| [50] | Wu X P, Wang T T. 2002. Progress of study on 3D Resistivity inversion methods[J]. Progress in Geophysics (in Chinese), 17(1):156-162. |
| [51] | Wu X P. 2005. 3-D resistivity inversion under the condition of uneven terrain[J]. Chinese Journal of Geophysics (in Chinese), 48(4):932-936. |
| [52] | Xiong B, Ruan B Y, Luo Y Z. 2003. 3-D numerical simulation study of DC resistivity anomaly under complicated terrain[J]. Geology and Prospecting (in Chinese), 39(4):60-64. |
| [53] | Yan J Y, Meng G X, Lü Q T, et al. 2012. The progress and prospect of the electrical resistivity imaging survey[J]. Geophysical and Geochemical Exploration (in Chinese), 36(4):576-584. |
| [54] | Yang Z L, Zhang X, Jiang H L. 2007. Geological characteristics of Sizhuang gold deposit in Laizhou City of Shandong Province[J]. Land and Resources in Shandong Province (in Chinese), 23(5):6-10. |
| [55] | Zhang J, Mackie R L, Madden T R. 1995. 3-D resistivity forward modeling and inversion using conjugate gradients[J]. Geophysics, 60(5):1313-1325. |
| [56] | Zhuang H. 1998. Research on 3-D resistivity tomography (in Chinese)[D]. Changsha:Central South University of Technology. |
| [57] | 崔书学,袁文花. 2008.莱州市寺庄金矿区第二金矿富集带成矿规律[J].地质调查与研究, 31(3):186-191. |
| [58] | 崔益安,白宜诚,杜华坤. 2005.基于扩展总线的电法勘探数据采集仪器设计[J].中南大学学报(自然科学版), 36(2):288-292. |
| [59] | 戴前伟,江沸菠,董莉. 2014.基于汉南-奎因信息准则的电阻率层析成像径向基神经网络反演[J].地球物理学报, 57(4):1335-1334, doi:10.6038/cjg20140430. |
| [60] | 范翠松,李桐林,严加永. 2012. 2.5维复电阻率反演及其应用试验[J].地球物理学报, 55(12):4044-4050, doi:10.6038/j.issn.0001-5733.2012.12.016. |
| [61] | 何继善. 1997.电法勘探的发展和展望[J].地球物理学报, 40(S1):308-316. |
| [62] | 黄俊革. 2003.三维电阻率/极化率有限元正演模拟与反演成像[D].长沙:中南大学. |
| [63] | 黄俊革,王家林,阮百尧. 2006.三维高密度电阻率E-SCAN法有限元模拟异常特征研究[J].地球物理学报, 49(4):1206-1214. |
| [64] | 江玉乐,康万福,张楠,等. 2007.高密度电法在岩溶勘察中的应用[J].成都理工大学学报 (自然科学版), 34(4):452-455. |
| [65] | 李金铭. 2005.地电场与电法勘探[M].北京:地质出版社. |
| [66] | 刘斌,李术才,李树忱,等. 2012.基于不等式约束的最小二乘法三维电阻率反演及其算法优化.地球物理学报, 55(1):260-268, doi:10.6038/j.issn.0001-5733.2012.01.025. |
| [67] | 潘克家,汤井田,胡宏伶,等. 2012.直流电阻率法2.5维正演的外推瀑布式多重网格法[J].地球物理学报, 55(8):2769-2778, doi:10.6038/j.issn.0001-5733.2012.08.028. |
| [68] | 强建科,罗延钟. 2007.三维地形直流电阻率有限元法模拟[J].地球物理学报, 50(5):1606-1613. |
| [69] | 强建科,阮百尧,周俊杰. 2010.三维坑道直流聚焦法超前探测的电极组合研究[J].地球物理学报, 53(3):695-699, doi:10.3969/j.issn.0001-5733.2010.03.024. |
| [70] | 阮百尧,熊彬. 2002.电导率连续变化的三维电阻率测深有限元模拟[J].地球物理学报, 45(1):131-138. |
| [71] | 吴小平. 1998.利用共轭梯度方法的电阻率三维正、反演研究[D].合肥:中国科学技术大学. |
| [72] | 吴小平,徐果明,李时灿. 1998.利用不完全Cholesky共轭梯度法求解点源三维地电场[J].地球物理学报, 41(6):848-855. |
| [73] | 吴小平,徐果明. 1999.电阻率三维反演中偏导数矩阵的求取与分析[J].石油地球物理勘探, 34(4):363-372. |
| [74] | 吴小平,徐果明. 2000.利用共轭梯度法的电阻率三维反演研究[J].地球物理学报, 43(3):420-427. |
| [75] | 吴小平,汪彤彤. 2002.电阻率三维反演方法研究进展[J].地球物理学进展, 17(1):156-162. |
| [76] | 吴小平. 2005.非平坦地形条件下电阻率三维反演[J].地球物理学报, 48(4):932-936. |
| [77] | 熊彬,阮百尧,罗延钟. 2003.复杂地形条件下直流电阻率异常三维数值模拟研究[J].地质与勘探, 39(4):60-64. |
| [78] | 严加永,孟贵祥,吕庆田,等. 2012.高密度电法的进展与展望[J].物探与化探, 36(4):576-584. |
| [79] | 杨之利,张旭,姜洪利. 2007.山东省莱州市寺庄金矿床地质特征[J].山东国土资源, 23(5):6-10. |
| [80] | 庄浩. 1998.三维电阻率层析成像研究[D].长沙:中南工业大学. |
 2015, Vol. 30
2015, Vol. 30


