地球物理学进展  2015, Vol. 30 Issue (4): 1935-1940   PDF    
引用本文
席道瑛, 徐松林, 王鑫,等. 高孔隙岩石局部变形带的简化模型. 地球物理学进展, 2015, 30(4): 1935-1940, doi: 10.6038/pg20150455  
XI Dao-ying, XU Song-lin, WANG Xin,et al. A simpified model of local deformation band for high porous rock. Progress in Geophysics(in Chinese), 2015, 30(4): 1935-1940, doi: 10.6038/pg20150455   
高孔隙岩石局部变形带的简化模型
席道瑛1, 徐松林2, 王鑫1, 宛新林3    
1. 中国科学技术大学 蒙城地球物理国家野外观测站 地球和空间科学学院, 合肥 230026;
2. 中国科学技术大学 中国科学院材料的力学行为和设计重点实验室, 合肥 230027;
3. 安徽建筑大学 土木工程学院, 合肥 230022
收稿日期: 2014-08-18 修回日期: 2015-02-06 .
基金项目：国家自然科学基金资助项目(11472264,11272304,40874093)资助.
作者简介：席道瑛,女,1940年生,1962年毕业于成都地质学院地球物理勘探专业,现任教授、博士生导师,主要从事岩石物理及本构模型方面的教学与研究工作.(E-mail:xdy@ustc.edu.cn)
摘要：用屈服函数和势能函数的偏导数重新定义了岩石的局部化变形带的判定条件,给出了新的局部化变形条件及临界模量.通过对Rudnicki和Rice(1975)为研究剪切带发生条件而建立的本构关系加以改进并放宽限定条件,提出了用四分之一椭圆帽盖模型以及与之相切的圆来简化势能函数,获得了简化模型,并在此简化模型基础上,取得了变形带发生的判定条件以及简化后的临界模量.同时还给出了简化理论模型的结果;通过压缩带和剪切带的产生顺序以及判定条件验证了简化模型的正确性,并与Issen等(2001)的理论模型进行了对比,讨论了简化模型的优越性以及在三轴对称压缩试验中的实用性.
关键词： 高孔隙岩石     局部变形带     简化模型     椭圆帽盖模型    
A simpified model of local deformation band for high porous rock
XI Dao-ying1, XU Song-lin2, WANG Xin1, WAN Xin-lin3    
1. Mengcheng geophysical national field station, school of earth and Space Sciences, University of Science and Technology of China, Hefei 230026, China;
2. CAS key laboratory of mechanical behavior and design, University of Science and Technology of China, Hefei 230027, China;
3. Civil engineering college, Anhui Jianzhu university, Hefei 230022, China
Abstract: Using the partial derivative of yield function and potential function redefine the criterion of rock deformation localization band, the new local deformation condition and critical modulus are given. Through the improvement and relax restrictions on constitutive relation which are founded by Rudnicki and Rice (1975) to study the shear bands occurring conditions, proposed to use 1/4 elliptical cap model and the tangent circles to simplify the potential energy function, obtained a simplified model, and on the based of this simplified model, gain the determinant condition of deformation belt occur and the simplified critical modulus. At the same time also gives the simplified theoretical model results; By the generating sequential of compression and shear zone and determination conditions verify the correctness of the simplified model, compared with the theoretical model of Issen and Rudnicki (2001), discussed the superiority of the simplified model and the utility in the three axisymmetric compression tests.
Key words: high porous rock     the local deformation band     simplified model     elliptical cap model    
0 引言

多孔岩石材料是构成地球的基本介质.与多孔岩石物理力学性能密切相关的是多孔岩土介质内部局部化变形的产生和演化.这些局部化变形的发展导致岩土介质呈现丰富的宏观变形形态和力学性能.其中最具特色的是剪切条带(shear b and )、压缩条带(compaction b and )和膨胀条带(dilation b and ).研究最早的是剪切带，由于韧性剪切带是金矿床控矿机制(Boyle，1979)其在金属成矿等领域起的特殊作用，引起了极大关注，相应的研究比较系统.实验研究和相关的分岔分析理论分析表明(徐松林等，2001，2002; 徐松林和吴文，2004)：由于岩土材料的特殊之处，在单轴和常规三轴加载条件下，岩土材料加载过程至少存在3个临界状态，即：峰值前的偏离线弹性段的岩石弱化点，对应于方程的椭圆型解；峰值处的岩石极限强度点，对应于方程的抛物型解；峰值后的岩石破坏点，对应于方程的双曲型解.这些研究对岩石材料复杂的强度表现给出了很好的解释.比较而言，压缩条带、膨胀条带是近年来才在野外被发现(李廷等，2008; Katsman and Aharonov，2006).压缩带和膨胀带与地震时的摩擦滑动连在一起(Di Toro et al.，2006; Rice，2006; 席道瑛和徐松林，2012)；而且压缩条带和膨胀条带关系到核废料的长期储藏和泄漏，与人们的健康和生命安全息息相关，还影响地下流体的储藏和输运(李廷等，2008).Rudnicki课题组(Rudnicki and Rice，1975; Issen，2000; Issen and Rudnicki，2000，2001; Rudnicki，2004)对剪切条带、压缩带条和膨胀带的形成和相互转化条件进行了较系统地研究，王鑫(2006)，席道瑛等(2008，2014)对局部化变形带的理论进行了较系统的论述.近期主要关注微观变形和相应的微力学机制的研究(Fortin et al.，2009; Zhu et al.，2010; Ji et al.，2012; Skurtveit et al.，2013).但这些理论相对比较复杂，本文将对Rudnicki和Rice(1975)较复杂的模型进行改进与简化，获得改进后的简化模型(王鑫，2006).

1 对Rudnicki和Rice模型的改进与简化 1.1 以屈服函数的偏导数定义判定条件

Rudnicki和Rice(1975)为了解释脆性岩石剪切带的形成，发展了基于塑性力学的局部化变形的分岔理论分析，得到由于在均匀介质中的局部化变形是因为本构关系的不稳定性.当席道瑛等(2008)的本构方程(7)具有非平凡解时，局部化变形形态在平面内表现出多种分岔变形形态.

Rudnicki和Rice(1975)定义剪切带的 发生条件时是以含Fσ、F、Γσ和Γ的如下表达式来定义的，公式为

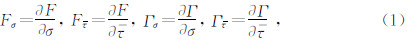
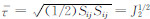其中，F为屈服函数，Γ为塑性势函数，σ为正应力，τ为剪应力为等效剪应力(席道瑛等，2008)，Sij为偏应力，若满足:

则不发生剪切带，这时压缩带成为唯一的局部化变形模式为

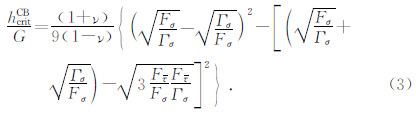
体积硬化模量h小于式(3)给出的临界模量时，将只可能发生压缩带.

将席道瑛等(2008)的式(18)和(21)中有关μ和β的定义代入式(27)得到的结果与本文判定条件式(3)相同.对于常规三轴压缩实验，可取NII=.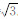

当应力状态处在屈服状态下，Fσ=Γσ，式(3)的首项为0，此时h < 0，则压缩带的σ~ε曲线斜率是负的.

当不满足式(2)时，有可能压缩带和剪切带都同时发生，此时压缩带的临界模量hcritCB自然由式(3)给出，而剪切带的临界模量hcritCB为

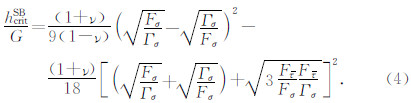
因为塑性变形的过程中模量h一般是单调递减的，所以岩石的局部化变形发展中首先产生的是临界模量较大的类型的变形带，对于常规三轴压缩实验时，产生剪切带时的临界模量hcritCB大于产生压缩带时的临界模量hCBcrit.当二者都可能存在时，由于二者的模量相比，剪切带的临界模量hcritCB较大，在实验过程中单调递减的模量随着压缩的进行，将先达到剪切带的hcritCB，然后再达到压缩带的hCBcrit.可见，首先会产生剪切带，然后才会产生压缩带.

剪切带的带角(条带的法线与最大压应力之间的夹角)为

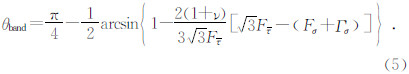
根据席道瑛等(2008)中式(28)的表述，如果满足:

则膨胀带有可能出现，其相应的临界模量为

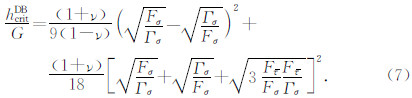
不过对于常规三轴压缩试验，席道瑛等(2008)中式(28)、(29)、(31)中的μ+β以及上式中的Fσ、F、Γσ不可能满足膨胀带产生时所需要满足的值域范围，故此文献Issen(2000)和席道瑛等(2008)中所用的NI=NII=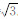，以及NIII= 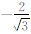的假定就不再适用.所以本文下面的改进模型中不再涉及膨胀带的问题.

1.2 对帽盖模型及塑性势能曲线的简化

帽盖模型最早是由剑桥大学Roscoe教授等在1958—1963年期间，针对流经剑桥大学的剑河的湿粘土而提出的，是第一个系统地将Mohr—Coulomb破坏准则、正交法则及加工硬化规律应用于土的弹塑性硬化模型(席道瑛等，2015).后来由Baron和Swanson(1970)与Swanson(1970)首次建立了美国Cedar城的英云闪长岩的帽盖模型，将其推广应用于岩石，让剪切破坏曲线与塑性势能曲线相切.它最简单的形式莫过于用四分之一椭圆来描述，本文拟将运用该方法，不考虑与非弹性变形历史有关的αk，而把屈服函数F仅仅看成是对σ和τ的函数，并引入塑性势能函数的简化假设，以此对Rudnicki和Rice(1975)模型进行分析，而获得局部化变形带的简化判定条件.

在如图 1坐标系下，用长短轴分别为a和b的一个椭圆来描述帽盖模型.根据常规三轴压缩试验的加载特性，图中由σc开始直指椭圆的一条直线是模拟常规三轴压缩试验的加载路径(Rudnicki，2004).

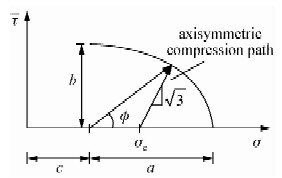图 1 帽盖模型的四分之一椭圆 Fig. 1 The 1/4 ellipse of hat model

由图可知，屈服面的方程为

由此可得:

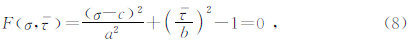
在塑性势能表达的框架下，对Rudnicki和Rice(1975)及Issen和Rudnicki(2001)的模型进行简化.

对应塑性势能曲线必须满足下面三个条件(Rudnicki，2004; 席道瑛等，2014):

①=0时，塑性势能曲线与σ轴垂直相交；

②-σ平面上，当=max时，Γσ=0；

③ 当屈服线与势能线同时都满足时，两曲线相切，它们具有同一法线.

用一个圆心在(σ0，0)，半径为r的圆，该圆同时还满足上述三个条件，以此来简化塑性势能曲面，如图 2所示，公式为

那么可以获得:

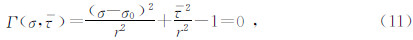
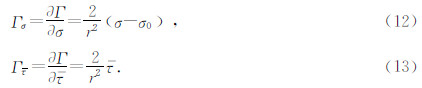
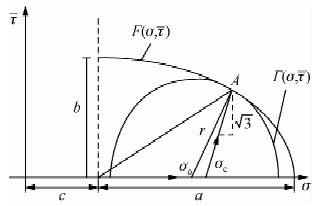图 2 椭圆曲面模拟塑性势能函数和屈服函数 Fig. 2 The plastic potential function and the yield function

由图 2中的常规三轴压缩(Rudnicki and Rice，1975)，可得:

当处于屈服状态时：Fσ=Γσ，由此可得:

再由式(14)、(15)及屈服点上F=Γ代入式(3)，可将式(6)写为

设椭圆的长轴与短轴之比为

并定义：

那么可有:

当此条件得到满足时，只产生压缩带，其相应的临界模量为

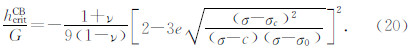
若不满足此条件时，压缩带和剪切带都可能产生，其式(20)仍为压缩带的临界模量，则剪切带的临界模量为

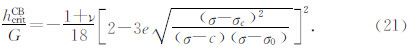
若将(15)、(18)分别代入(20)、(21)还可取得压缩带和剪切带的临界模量的三维信息为

2 简化模型的合理性，优越性的检验

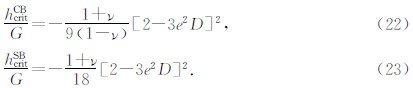
根据式(18)，可得知:[2-3e2D]2 < 1，对砂岩来说，泊松比ν≈0.2~0.3，由此可见剪切带的临界模量hcritSB要大于压缩带的临界模量hCBcrit，我们知道硬化模量h又是单调递减的，故此随着常规三轴压缩的进行，硬化模量h先达到剪切带的临界模量hcritSB，产生剪切带，然后才达到压缩带的临界模量hcritCB，再后才可能产生压缩带.这与Issen和Rudnicki(2000)对压缩带和剪切带发生的条件及产生顺序的判定相符(即式(3)和式(4))，这足以说明我们的简化模型是正确的、合理的.

以下以简化模型来处理Issen(2000)的局部化变形带的判定条件.简化模型为

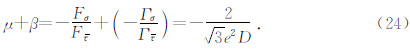
由式(19)，De2 < 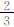，所以β+μ < 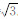－，它的边界条件β+μ=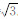－与席道瑛等(2008)中式(29)中不具有剪切带只具有压缩带的判定条件与之相一致.充分说明简化模型在局部化变形带的判定条件的处理时是合理的，由此证明了我们的简化模型也是合理的.

图 3是简化模型的局部化变形带的判定条件式式(19)，横坐标e= 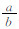为椭圆的长短轴之比，纵坐标为D，图中浅色部分只能允许压缩带的部分出现，图中深色部分是均可能出现压缩带和剪切带的部分.由式(18)D的定义可以得知：D的值处于(0，1)之间，所以e的值域范围> 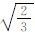，根据实际情况，图中仅画到e=10.

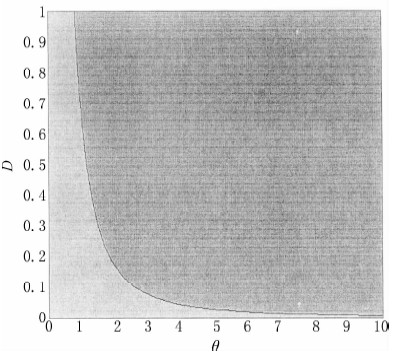图 3 简化模型的局部化变形带的判定条件 Fig. 3 The determinant conditions of local deformation band under simplified model

由式(24)分析得到μ+β的值，再根据局部化变形带的判定条件式(19)，获得了简化模型下μ+β的值域三维图，见图 4.μ+β为垂直轴，可见图中的三维平面图是在局部化变形带判定条件下μ+β的临界曲面.在三维临界曲面之上的部分都可能是压缩带和剪切带出现的区域，而三维临界曲面之下的部分是仅可能出现压缩带的区域.

图 4 简化模型的三维临界曲面图 Fig. 4 The 3D graph of μ+β under simplified model

下面继续引用Issen和Rudnicki(2000)对于局部化变形带所给出的判定条件与β和μ的关系，并根据β和μ的取值范围，进一步给出了图 5，图 6、图 7所示的β+μ的三维曲面.

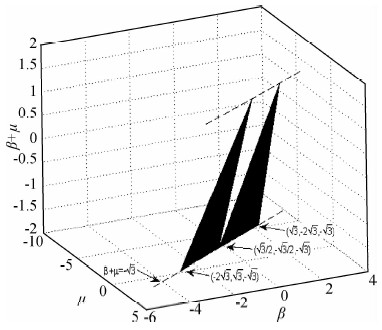图 5 Issen和 Rudnicki (2000)理论中剪切带发生的β+μ值域范围 Fig. 5 The value of β+μ in Issen’s theory of shear band

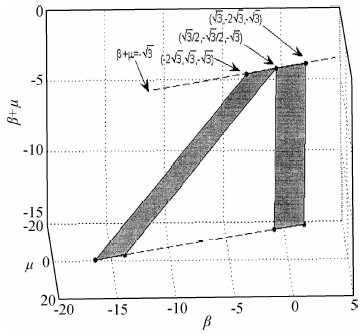图 6 对应图5的压缩带发生的β+μ值域范围 Fig. 6 The value of β+μ in theory of compaction band corresponding to Fig.5

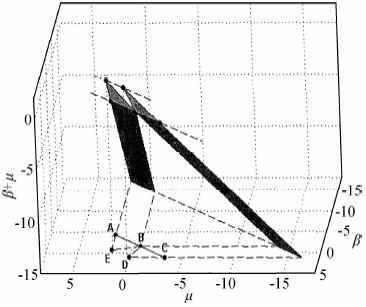图 7 Issen和 Rudnicki (2000)理论中剪切带和压缩带发生的联合β+μ值域范围 Fig. 7 The joint range of β+μ in theory of shear zone and compaction band (Issen and Rudnicki, 2000)

图 5的两个三角形区域是Issen和Rudnicki(2000)的局部化变形理论中剪切带可能发生的范围，正如图所示β+μ=-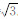这个临界条件，为三角形的底边.

图 6的一个黑色的平行四边形和一个矩形组成的一个梯形，两个黑色区域是Issen和Rudnicki(2000)的局部化变形理论中压缩带可能发生的范围，如图所示β+μ=-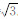这个临界条件是两个黑色区域组成的梯形的一条公用的上顶边.

图 7是Issen和Rudnicki(2000)的局部化变形理论中剪切带和压缩带都可能发生的区域图，下部深色的部分是发生压缩带时β+μ的取值范围，上部较浅色的部分是发生剪切带时β+μ的取值范围.图 7中的值域范围在β和μ平面内的投影与席道瑛等(2008)的图 6一致.

如果将图 5、图 6、图 7与图 4进行比较，就可以清楚发现Issen和Rudnicki(2000)的局部化变形理论中的判定条件，仅讨论了μ+β的值域范围以及μ和β各自的取值范围，而没能体现出β和μ之间的关系；仅仅给出了边界条件β+μ=-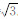，而忽略了在加载过程中β和μ会发生变化，而这个加载过程给β和μ带来的相互影响.在笔者的简化模型中，由于变形带的范围以及β+μ值的范围有确切的表达式，可以直观地显现出D和e的相互关系，它们之间这一关系是由一函数关系来限定的，因此更加直观清晰明了.如果笔者能对常规三轴压缩试验的全程进行观察，求取D和e在该过程的变化，并验证和改进本文的简化模型，很有可能求得D和e的函数关系，这样就能更准确的反映出常规三轴压缩试验中的局部化变形带产生的判定条件.因此，笔者认为，简化模型与Issen和Rudnicki(2000)的理论模型相比具有直观、简单、使用方便的优势.

此外，在常规三轴压缩试验过程中，笔者通过测量屈服状态时与σ记录的试验数据来拟合以为纵轴σ为横轴的平面内的屈服面和塑性势面，并获得c值，根据图 1就很易取得椭圆的长轴a、短轴b、σc值，再通过式(17)、(18)计算得到e和D值，然后可用e和D的关系来确定局部变形带的产生条件.而Issen和Rudnicki(2000)的模型中是根据一个较复杂的计算方法，用试验数据分别计算β和μ，再用μ+β及β和μ各自的取值范围来判断局部化变形带的发生.由于在常规三轴压缩试验中一般情况下很少采用循环加载，导致塑性形变计算的复杂化，从而也引起β和μ的计算的复杂化.因此，笔者认为，简化模型在实际问题的分析中使用比较方便，如对高孔隙岩石的常规三轴压缩试验分析中什么时候出现什么样的局部化变形带时，本文的简化模型将会比Issen和Rudnicki(2000)的理论模型更简便更具实用性.

3 结论与讨论 3.1         在席道瑛等(2008)对局部化变形带的理论进行描述的基础上，对Rudnicki和Rice(1975)建立的剪切带发生条件的本构关系，放宽了它的限定条件进行了进一步的改进，获得了一个相对简单的关于剪切带、压缩带和膨胀带的发生条件的判定关系和临界模量.在此基础上，又从Rudnicki和Rice(1975)模型出发，引进帽盖模型，并用四分之一椭圆对“帽盖”模型的屈服函数(即“帽盖”)进行简化和与之相切的圆来简化塑性势能函数，对其进行了简化和改进，获得了简化模型下的局部化变形带产生方向的判定条件以及简化后的临界模量.同时还给出了上述复杂理论模型改进后的结果；本文还通过压缩带和剪切带发生的判定条件及产生的顺序，并与Issen et al.(2001)的判定条件相对比，检验了简化模型的正确性.还对两种模型进行了比较，从直观上看简化模型一目了然，在实际应用中较为方便，因此具有简单，使用方便更具实用性的优越条件.

3.2         我们的简化模型的变形带范围及β+μ值范围都具有确切的表达式，若对常规三轴压缩试验进行全过程观察，还能直接给出D和e的相互关系，就能更准确的反映常规三轴压缩试验中的局部化变形带产生的判定条件.可见简化模型与Issen和Rudnicki(2000)的理论模型相比具有一定的优势.

3.3         由于本文式(7)中的Fσ、Fτ、Γσ不满足膨胀带产生所需要满足的值域范围，所以，该简化模型还不能预测膨胀带的产生.

致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持！
参考文献
[1] Baron M L, Swanson S R. 1970. Constitutive equations for rock based on Experimental measurements of stress-strain and fracture properties[C].//Presented at the DASA long-Ronge Planning Meeting, Albuquerque. New Mexico.
[2] Boyle R W. 1979. The geo-chemistry of gold and its deposits[M]. Geological Survey of Canada, Bulletin 280.
[3] Di Toro G, Hirose T, Nielsen S, et al. 2006. Natural and experimental evidence of melt lubrication of faults during earthquakes[J]. Science, 311(5761): 647-649.
[4] Fortin J, Stanchits S, Dresen G, et al. 2009. Micro-mechanisms involved during inelastic deformation of porous carbonate rocks[C].//Proceedings of the 4th Biot Conference on Poromechanics. New York, 378-388.
[5] Issen K A. 2000. Conditions for localized deformation in compacting porous rock[Ph. D. Thesis]. Evanston: Northwestern University.
[6] Issen K A, Rudnicki J W. 2000. Conditions for compaction bands in porous rock[J]. Journal of Geophysical Research, 105(B9): 21529-21536.
[7] Issen K A, Rudnicki J W. 2001. Theory of compaction bands in porous rock[J]. Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy, 26(1-2): 95-100.
[8] Ji Y T, Baud P, Vajdova V A, et al. 2012. Characterization of pore geometry of indiana limestone in relation to mechanical compaction[J]. Oil & Gas Science and Technology, 67(5): 753-775.
[9] Katsman R, Aharonov E. 2006. A study of compaction bands originating from Cracks, notches, and compacted defects[J]. Journal of Structural Geology, 28(3): 508-518.
[10] Li T, Du Y, Wang X, et al. 2008. Field evidence and experimental research on localized deformation bands in high-porosity rocks[J]. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 27(S1): 2593-2604.
[11] Rice J R. 2006. Heating and weakening of faults during earthquake slip[J]. Journal of Geophysical Research, 111(B5): B05311.
[12] Rudnicki J W. 2004. Shear and compaction band formation on an elliptic yield cap[J]. Journal of Geophysical Research, 109(B3): B03402.
[13] Rudnicki J W, Rice J R. 1975. Conditions for the localization of deformation in pressure-sensitive dilatant materials[J]. J. Mech. Phys. Solids, 23(6): 371-394.
[14] Skurtveit E, Torabi A, Gabrielsen R H, et al. 2013. Experimental investigation of deformation mechanisms during shear-enhanced compaction in poorly lithified sandstone and sand[J]. Journal of Geophysical Research: Solid Earth, 118(8): 4083-4100, doi: 10.1002/jgrb.50342.
[15] Swanson S R. 1970. Development of constitutive equations for rock[Ph. D. Thesis]. Utah: University of Utah.
[16] Wang X. 2006. Study on local deformation of high-porosity rock using bifurcation theory (in Chinese)[Master Dissertation]. Hefei: University of Science and Technology of China.
[17] Xi D Y, Du Y, Li T, et al. 2008. Research progress in theory and forming condition of localized deformation bands in high-porosity rock[J]. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 27(S2): 3888-3898.
[18] Xi D Y, Xu S L. 2012. Foundations of Rock Physics (in Chinese)[M]. Hefei: University of Science and Technology of China Press, 186-194.
[19] Xi D Y, Xu S L. 2015. Constitutive Theory of Porous Rocks and Soil Material (in Chinese)[M]. Hefei: University of Science and Technology of China Press, 264-267.
[20] Xu S L, Wu W. 2004. Bifurcation analysis on deformation localization of geomaterials[J]. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 23(20): 3430-3438.
[21] Xu S L, Wu W, Zhang Q H, et al. 2002. Bifurcation analyses of finite/large deformation for a marble[J]. Chinese Journal of Geotechnical Engineering (in Chinese), 24(1): 42-46.
[22] Xu S L, Wu W, Li T, et al. 2001. Experimental studies on localization and bifurcation behaviors of a marble under triaxial compression[J]. Chinese Journal of Geotechnical Engineering (in Chinese), 23(3): 296-301.
[23] Zhu W, Baud P, Wong T F. 2010. Micromechanics of cataclastic pore collapse in limestone[J]. Journal of Geophysical Research, 115: B04405, doi: 10.1029/2009JB006610.
[24] 李廷, 杜赟, 王鑫,等. 2008. 高孔岩石局部变形带的野外证据和实验研究进展[J]. 岩石力学与工程学报, 27(S1): 2593-2604.
[25] 王鑫. 2006. 利用分岔分析理论研究高孔隙度岩石的局部化变形[硕士学位论文]. 合肥: 中国科学技术大学.
[26] 席道瑛, 杜赟, 李廷,等. 2008. 高孔岩石中局部变形带的理论和形 成条件研究进展[J]. 岩石力学与工程学报, 27(S2): 3888-3898.
[27] 席道瑛, 徐松林. 2012. 岩石物理学基础[M]. 合肥: 中国科学技术大学出版社, 186-194.
[28] 席道瑛, 徐松林. 2015. 多孔岩土材料的本构理论[M]. 合肥: 中国科学技术大学出版社, 264-267.
[29] 徐松林, 吴文. 2004. 岩土材料局部化变形分岔分析[J]. 岩石力学与工程学报, 23(20): 3430-3438.
[30] 徐松林, 吴文, 张奇华,等. 2002. 大理岩有限变形分岔分析[J]. 岩土工程学报, 24(1): 42-46.
[31] 徐松林, 吴文, 李廷,等. 2001. 三轴压缩大理岩局部化变形的试验研究及其分岔行为[J]. 岩土工程学报, 23(3): 296-301.