2. 山东大学 岩土与结构工程研究中心, 济南 250061
2. Geotechnical and Structural Engineering Research Center, Shandong University, ji'nan 250061, China
航空瞬变电磁是一种具有速度快、成本低,无需地面人员接近等显著优点的地球物理勘探方法,其应用领域已经从传统的地质调查、地下水监测扩展到金属矿探测、环境保护和工程勘察等应用领域.航空瞬变电磁一次工作覆盖工区范围广,采集的数据量巨大.丰富的信息,对于剖面拟地震成像解释有很大的优势.拟地震成像解释不仅计算速度快,能够实现实时成像,而且方法具有较好的成层性,有利于对地下介质的电性界面进行识别.这对于航空瞬变电磁的应用推广领域拓展十分有益.
航空瞬变电磁早期解释方法主要是针对视电阻率参数进行近似反演,根据具体的实现过程的不同可以分为以下类型:视电阻率转换方法基于视电阻率计算和趋肤深度公式,以视电阻率作为输入,直接得到电阻率和深度,且方法不需要初始模型,查表以及迭代等辅助过程(Huang and Fraser,1996);Klaus等人(2000)通过重新定义视电阻率和深度,用一种反演方法来提高测量曲线对电阻率垂向变化的分辨率.CDT即电导率深度转换方法,该方法成果丰富,主要有:Macnae等(1998)提出的EMFLOW并形成了软件系统;Fullagar and Reid(2001)提出的Emax CDT法;Zhdanov等(2002)给出了S-inversion方法;以及更早的Wolfgram and Karlik(1995),Liu and Asten(1993)等也分别提出来各自的CDT反演方法.除此之外还有,Wolfgram等(2003)对拟二维航空瞬变电磁法反演做了研究,采用了波恩近似的方法,实现了快速反演.Sattel(2005)用Zohdy方法模拟航空瞬变电磁法资料.虽然近似反演方法计算速度快,但是该类方法抗干扰能力差,而航空瞬变电磁信噪比较地面瞬变电磁法小,容易受噪声影响,因此当噪声相对较大时,利用近似算法对受噪声影响航空瞬变电磁数据进行解释得到的结果往往失实.近些年,国外实测航空瞬变电磁数据解释大多采用一维反演,主要为层状模型反演类方法(Chen and Raiche,1998; Farquharson et al.,2003;Christensen et al.,2010).最近,随着勘探精度的提高亦有一些三维反演方法被提出,但是由于三维正演计算十分耗时,较早的航空电磁三维正演计算均采用了近似算法进行加速(Zhdanov and Tartaras,2002;Zhdanov and Chernyavskiy,2004),直到moving footprint思想的提出,3D航空瞬变电磁反演才得以真正实现(Zhdanov et al.,2004;Cox et al.,2010),但是该方法仍需要在较高配置的工作站中完成,且耗时较长.在国内,航空电磁正反演方法也已经蓬勃发展,罗延钟等(2003)导出了层状介质偶极装置条件下的时域航空电磁法的正演计算公式.强建科等(2010)实现了航空瞬变电磁的一维正反演以及全时域视电阻率定义;毛立峰等(2011)提出了航空瞬变电磁自适用正则化一维反演,方法可以实现地电模型与高度的同时反演.陈小红和段奶军(2012)研究了航空瞬变电磁的快速成像.朱凯光等(2008,2010)研究了频率域航空正演,并且基于主分量分析的神经网络反演实现了时间域航空瞬变电磁的解释.殷长春等(2013,2014)实现了航空电磁的全时域正演,并利用贝叶斯法实现了航空电磁反演.总之,反演算法较近似解释方法受噪声影响小,但是计算速度慢,尤其是航空电磁覆盖面积广、数据量大,进行反演解释耗时更多,不适合实时成像,而且上述所有方法都是以单点数据为依据进行解释处理,没有较好的利用不同测点数据间的相关性.为了避免上述问题,亟需一种既能有效避免干扰影响,又能够快速准确的对地下介质进行实时成像的处理技术.
本文基于等效导电平面原理结合相关加权叠加合成孔径技术,实现一种快速成像的航空瞬变电磁快速解释算法.首先依靠相邻点之间的相关性采用相关加权叠加的方法进行孔径合成,将传统的单点解释拓展到多点相关联合解释,有效的压制了噪音的影响;此外,文中方法不仅具有较好的抗噪性,而且计算速度快,可以进行航空瞬变电磁的实时成像.
1 基本理论1.1 微分电导成像原理等效导电平面法是计算瞬变电磁响应的近似算法(Piao,1990;Li,2002),即利用一个导电薄板代替地下介质,根据镜像法计算空间任意点的瞬变电磁响应.如图 1所示,为等效导电平面解释示意图.
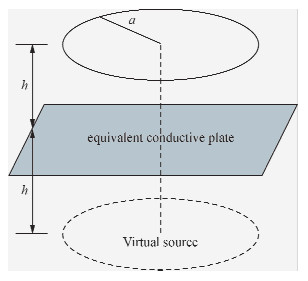 | 图 1等效导电平面示意图Fig. 1 Diagram of moving plate |
直升机吊舱式航空瞬变电磁法也可以利用等效导电平面法进行近似模拟,只是等效平面随时间下沉的速度不在是常数,而是与各层电导率和厚度有关的函数,其它方面与均匀半空间响应完全相似.
根据等效导电平面法可以得到航空瞬变电磁层状模型的视纵向电导定义与研究深度的计算公式为
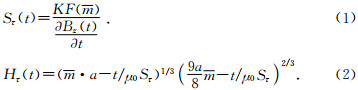
其中
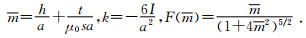
利用公式(1)和公式(2)可以实现航空瞬变电磁S参数解释.
在求得了Sτ(t)和Hτ(t)后,在每个测点上绘制Sτ(Hτ)曲线.Sτ(Hτ)为单调增曲线,随着曲线上升斜率的变化表示地下介质电导率的改变,转折点对应着电性界面的深度.对Sτ(Hτ)曲线关于深度求一阶导数得Sτ′(Hτ),Sτ′(Hτ)的拐点对应着地下电性分界面.对Sτ(Hτ)关于深度求二阶导数得,曲线的极值点对应着地下介质的电性分界面.因此曲线更利于对地下电性界面的分辨,称之为微分电导.
为了直观的比较Sτ(Hτ),Sτ′(Hτ)和曲线的关系,现给出A、H、K、Q四种三层模型的曲线对比结果,如图 2所示.
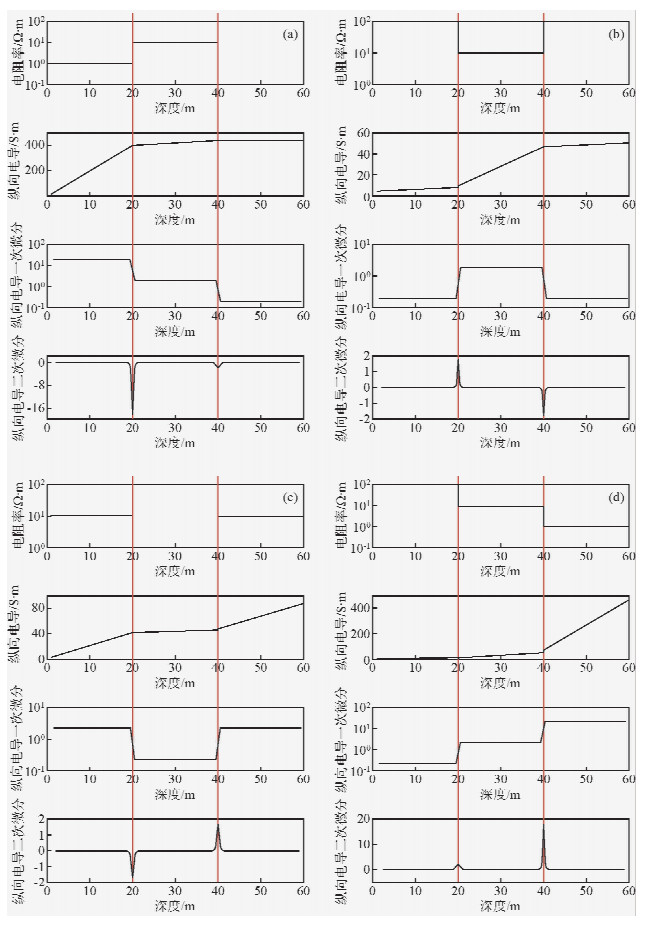 | 图 2 A、H、K、Q模型微分电导特性示意图
(a)A模型微分电导特性;(b)H模型微分电导特性;(c)K模型微分电导特性;(d)Q模型微分电导特性.Fig. 2 Analysis of differential conductance of A H K and Q model (a)A model;(b)H model;(c)K model;(d)Q model. |
获得航空瞬变电磁的微分电导数据后,根据合成孔径雷达思想,可以利用相关叠加孔径合成算法实现基于微分电导的合成孔径成像.
采用相关叠加的方法实现合成孔径算法,即计算不同测点信号的相关系数,生成不同的权函数,相邻各测点信号在做叠加时以最大相关系数为权进行相关加权,形成新的合成数据,如图 3所示为合成示意图,其中N表示合成孔径范围.
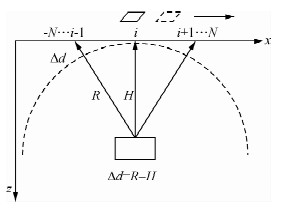 | 图 3 合成孔径示意图Fig. 3 Sketch map of synthetic aperture |
将上述过程写成数学表达式形式为
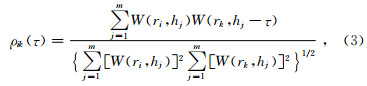
其中r为测点坐标,hj为视深度,τ为偏移距离,ρ表示相关系数,m为采样道数,k表示偏移点数,W为微分电导函数.
选择加权系数和最佳偏移距后,进行合成,表达式如(4)所示为
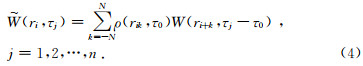
其中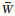 (ri,τj)为合成后数据,N为合成孔径范围.
(ri,τj)为合成后数据,N为合成孔径范围.
在进行相关叠加孔径合成时有几个关键参数需要选择,而参数的选择主要以相关系数为依据.
首先确定合成孔径的范围N.合成孔径范围有两种选择方式,一种为先验选择,另一种为根据不同点的相关系数后验选择.所谓先验选择即根据测点距离稠密程度和目标尺度,由研究者人为选择孔径长度.先验选择具有多值性,不同的人可能选择不同的合成长度,但是对于经验丰富的解释人员先验选择简单有效.所谓后验选择即是根据数据间相关程度ρ自动选择合成范围.首先计算各测点与待合成点之间的最大相关系数ρmax,以待合成点为中心向两侧逐步判断最大相关系数的值与相关阈值ρ的大小,若出现最大相关系数小于阈值则停止比较,取当前点的前一点为合成孔径的边界点.
最佳偏移τ0的确定是一个复杂的过程,因为偏移距与目标体深度有关,因此不能像SAR那样较准确的确定τ0.为了简化问题,我们依然从两点信号的相关度出发.在求得的相关系数函数中选择最大相关系数,并判断相关系数的时移,认为此偏移量即是最佳偏移距.
微分电导方法计算速度快,但是受噪声影响较大,尤其经过二次求导后使得微分电导对噪声的反应更加灵敏.但是相关叠加合成孔径算法可以有效压制噪声提高信噪比,如图 4所示设计一个H型地电模型,并添加高斯噪声如图 4a所示;计算得到的微分电导如图 4b;图 4c为求得的相关系数;进行合成,结果如图 4d所示.合成算法有效的压制了噪声,这是因为相同地质体的反射回波具有相关性,而干扰信号一般为随机噪声,不具有相关性.由此,重构的信号将地下介质信号加强的同时又压制了噪声.
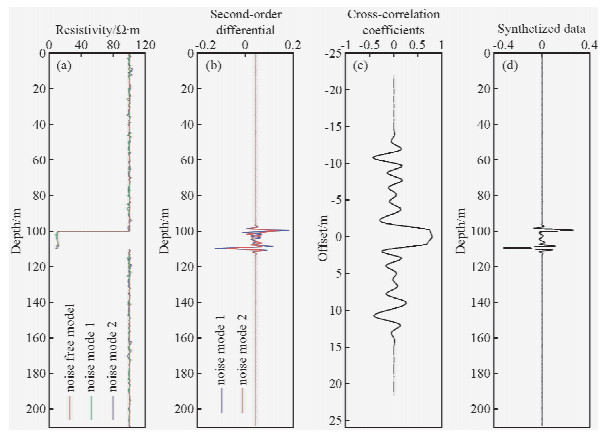 | 图 4 合成孔径效果分析
(a)含噪地电模型;(b)含噪的微分电导图;(c)互相关函数曲线;(d)合成后效果图.Fig. 4 Results of synthetic aperture (a)Geoelectric model with noise;(b)Differential conductance with noise;(c)Cross-correlation function;(d)Results of stack. |
以实际煤矿地层为基础,设计了含有两层煤以及两层采空区的三维复杂模型,两层煤层之间是砂质页岩,上层煤层顶部为细砂岩,下层煤层底部为石英砂岩,图 5即为两层采空区复杂模型立体图.图 5所示的地层厚度,异常体的尺寸以及地质体、地层的地电参数详细情况见表 1.
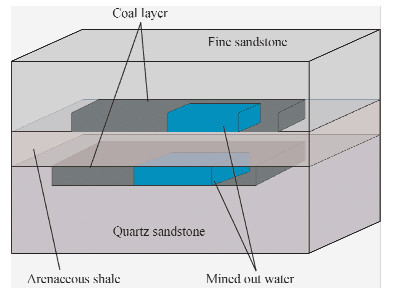 | 图 5 两层采空区复杂模型立体图Fig. 5 Space diagram of complex model with two gobs |
| 表 1 两层采空区复杂模型地电参数Table 1 Parameters of the complex model |
如图 6所示为两层采空区复杂模型俯视图,图中标明了测线位置,其中每条测线有31个测点.已知测量系统飞行高度为100米,采用三维时域有限差分法实现航空瞬变电磁法对三维两层采空区复杂模型的正演.文中仅对提取的三条典型测线进行分析,三条测线分别是,line133、line150、line169,其特征如下:Line133测线位于单层采空区上;line150 位于模型中部,覆盖两层采空区;line169 位于测区右侧,下部为均匀煤层,不含采空区.
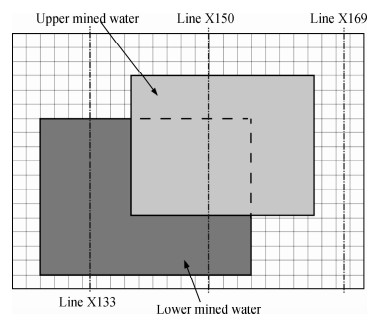 | 图 6 两层采空区复杂模型俯视图Fig. 6 Top view of the complex model with two gobs |
利用视电阻率定义方法对航空瞬变电磁正演数据进行处理,区域三维视电阻率断面图如图 7a所示,图 7b为视电阻率切片显示效果图.由图可知,可以看出在不同层位分布两个低阻异常,视电阻率结果初始设计的两层采空区模型相对应.但是仅从视电阻率图中并不能很好的显示出模型的地层分布.
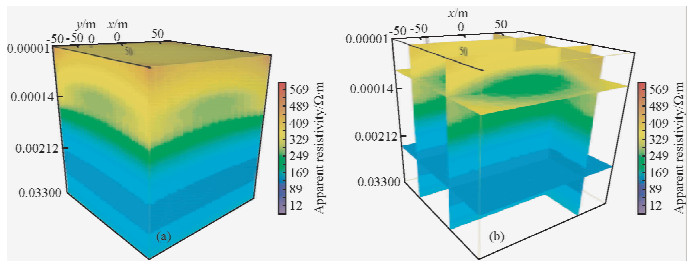 | 图 7 测区三维视电阻率图
(a)测区三维视电阻率图;(b)测区三维视电阻率切片显示效果图.Fig. 7 3D apparent resistivity of the survey area (a)3D apparent resistivity cross-section;(b)Slice map of apparent resistivity. |
测线line133位于测区左端,仅覆盖下层采空区.图 8a和b分别是测线line133的微分电导成像与作相关叠加处理后的解释结果.从图 8a微分电导成像图中可以看出在深度100 m处,有一强电性分解面,为空气与地层分解面;在深度为210 m、220 m、260 m、270 m处均有电性分界面分布,且210 m与220 m处上下层电性差别不大,这与模型地层分布及电性参数分布规律一致.在点号141~156,深度260~270 m位置电性与围岩电性差别较大,位置与下层采空区相符.由此可知,微分电导的极值与模型各层电性界面对应,由于含水采空区的存在使得采空区与围岩电性差异较大,这在图中显示为中间部分极值较大的同相轴.经过相关叠加处理后结果如图 8b所示,相关叠加将异常信息加强,并保持振幅放大倍数不变,不仅下层采空区位置可以明显的界定,而且图中清楚的给出了电性变化不大的上煤的两层界面信息.由此可知,相关叠加合成孔径可以增加若异常,提高分辨率.
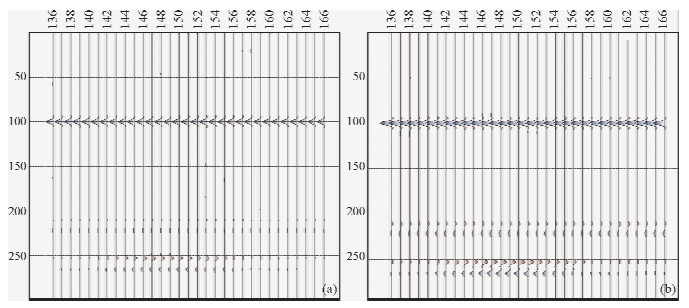 | 图 8 line133 微分电导与合成孔径成像成果图
(a)line133微分电导成像;(b)line133 相关叠加合成孔径成像.Fig. 8 Results of differential conductance and synthetic aperture of line133 (a)Differential conductance of line133;(b)Synthetic aperture of line133. |
测线line150位于测区的中部,覆盖两层采空区.图 9a和b分别为line150的微分电导成像与相关叠加合成孔径结果.微分电导结果能够清楚的给出电性界面和第一层采空区范围,但是对第二层采空区范围显示不明显.经过相关叠加处理并保持同相轴振幅放大倍数与图 9a一致,由图 9b可知,图中清楚了画出了两层采空区的边界范围.由此可知,相关叠加提高深部异常信息,提高方法的横向分辨率.
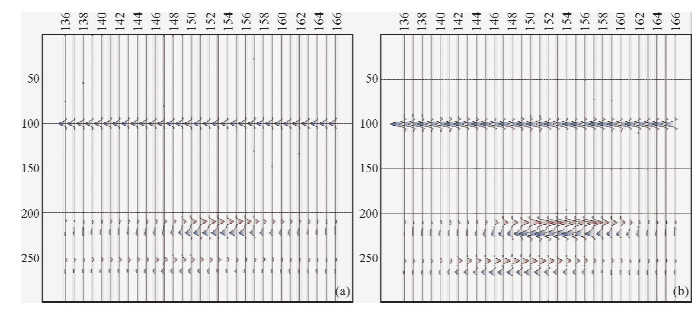 | 图 9 Line 150 合成孔径前后对比图
(a)line150 微分电导成像结果;(b)line150 相关合成成果图.Fig. 9 Results of differential conductance and synthetic aperture of line150 (a)Differential conductance of line150;(b)Synthetic aperture of line150. |
测线Line169 位于测区右端,仅覆盖测区背景场.图 10a和b分别是line169的微分电导和相关叠加合成结果.对比两图可知,经过相关合成后,图 10b对地层的显示较图 10a有很大改善.
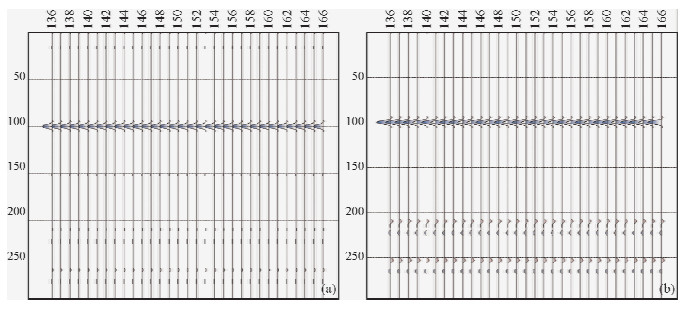 | 图 10 line169数据解释成果图
(a)line169微分电导成像结果;(b)line169相关叠加处理结果.Fig. 10 Results of differential conductance and synthetic aperture of line169 (a)Differential conductance of line169;(b)Synthetic aperture of line169. |
采用直升机吊舱系统在某小岛进行了野外实测实验.在地表铺设了多匝线圈作为异常.如图 11所示为实测数据多测道图.从图中可以清楚发现异常所在位置.图 12a为实验剖面的视电阻率图,由图可知,在380~480区间有一低阻贯穿,从异常位置可以推断为线圈异常引起.在80 m以深电阻率整体表现为低阻.在深度小于80米的表层区域,地下介质的电性变化不大,因此图 12b与图 12c浅部没有电性分界面.比较图 12b微分电导结果与图 12c的合成孔径成像结果,在浅部两者吻合较好,而在深部电性变化较大的区域,合成孔径成像结果不仅对低阻有一定的反应,更令人兴奋的是从图中可以清楚的看到深部地下地电结构分布的精细结果.
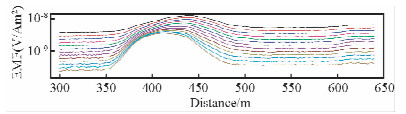 | 图 11 图 11 实测数据多测道曲线Fig. 11 Multi-channel data |
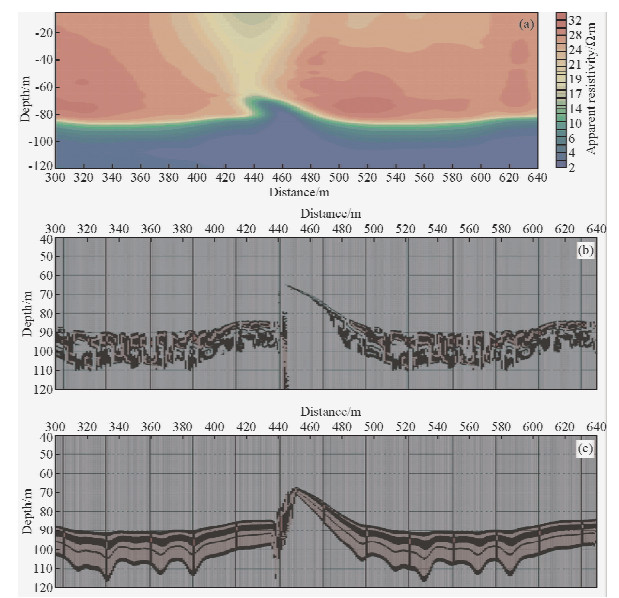 | 图 12 实测数据处理结果图
(a)实验数据视电阻率断面图;(b)实验数据微分电导图;(c)实验数据合成孔径成像.Fig. 12 Results of measured data (a)Apparent resistivity section;(b)Differential conductance of measured data;(c)Synthetic aperture of measured data. |
4.1 文中介绍了一种适用于直升机吊舱式航空瞬变电磁的快速成像算法.该方法的特点是将接收的衰减电压转换成微分电导,利用多点相关性质实现合成孔径,使用多个测点数据联合参与成像解释.航空瞬变电磁采集的数据量巨大,十分利于剖面拟地震成像解释,并且解释结果对于地层划分,电性分层等具有很大优势.
4.2 通过对数值模型和实测数据的分析可知,相同地质异常的响应具有很好的相关性,而噪声没有相关性,利用相关叠加合成方法确实能够增强地质体异常信号强度,压制噪声影响.因此相关叠加算法能够提高信噪比.
4.3 航空瞬变电磁相关叠加合成孔径成像快速算法继承了S参数反演快速算法的优点,并且具有较好的抗噪性能,因此该方法可以实时的对地下介质进行成像.实现实时成像后,航空电磁可以根据成像结果调整测区范围与测线方向,减少作业时间提高工作效率.这对航空瞬变电磁法开拓新的应用领域具有广阔前景.
致 谢 吉林大学林君教授及其科研团队提供了直升机航空瞬变电磁的实验数据,在此对林教授表示感谢.
| [1] | Beamish D. 2002. An assessment of inversion methods for AEM data applied to environmental studies[J]. Journal of Applied Geophysics, 51(2-4):75-96. |
| [2] | Cao J P, Rudd J. 2003. Conductivity-depth imaging of helicopter-borne TEM data based on a pseudolayer half-space model[J]. Geophysics, 73(3):F115-S120. |
| [3] | Cheng X H, Duan N J. 2012. Study on fast imaging of airborne time-domain electromagnetic data[J]. Progress in Geophysics (in Chinese), 27(5):2123-2127, doi:10. 6038/j.issn.1004-2903.2012.05.037. |
| [4] | Constable S C, Parker R L, Constable C F. 1987. Occam's inversion:A practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 52(3):289-300. |
| [5] | Cox L H, Zhdanov M S. 2008. Advanced computational methods of Rapid and Rigorous 3-D inversion of airborne electromagnetic data[J]. Commun. Comput. Phys., 3(1):160-179. |
| [6] | Cox L H, Wilson G A, Zhdanov M S. 2010. 3D inversion of airborne electromagnetic data using a moving footprint[J]. Exploration Geophysics, 41(4):250-259. |
| [7] | Cumming I G, Wong F H. 2005. Digital Processing of Synthetic Aperture Radar data:Algorithms and Implementation[M]. Boston, MA:Artech House. |
| [8] | Fang W Z, Li Y G, Li X. 1993. Theory of transient electromagnetic method sounding (in Chinese)[M]. Xi'an:Northwestern Polytechnical University Press, 66-68. |
| [9] | Fullagar P K, Reid J E. 2001. Emax conductivity-depth transformation of airborne TEM data[C].//15th Conference and Exhibition, ASEG Extended Abstracts. Brisbane, 1-4. |
| [10] | Fullagar P K, Vrbancich J,Pears G.2010. Geologically-constrained 1D TEM inversion[C].//21st International Geophysical Conference & Exhibition, ASEG Extended Abstracts, Sydney, 1-4. |
| [11] | Huang H P, Fraser D C. 1996. The differential parameter method for multifrequency airborne resistivity mapping[J]. Geophysics, 61(1):100-109. |
| [12] | Lee J B, Dart D L, Turner R J, et al. 2002. Airborne TEM surveying with a SQUID magnetometer sensor[J]. Geophysics, 67(2):468-477. |
| [13] | Legault J M, Witter J B, Berardelli P, et al. 2010. ZTEM airborne AFMAG EM results over the Reese River geothermal test area, central Nevada[C].//21st Geophysical Conference, ASEG Extended Abstracts, 1-4. |
| [14] | Li X. 2002. Theory and application of transient electromagnetic sounding (in Chinese)[M]. Xi'an, China:Shaanxi Science and Technology Press. |
| [15] | Li X, Quan H J, Xu A X, et al. 2003. Differential coefficient imaging of the longitudinal conductance in the transient electromagnetic sounding[J]. Coal Geology and Exploration (in Chinese), 31(3):59-61. |
| [16] | Li Y X, Qiang J K, Tang J T. 2010. A research on 1-D forward and inverse airborne transient electromagnetic method[J]. Chinese J. Geophys. (in Chinese), 53(3):751-759, doi:10.3969/j.issn.00015733.2010.03031. |
| [17] | Luo Y Z, Zhang S Y, Wang W P. 2003. A research on one-dimension forward for aerial electromagnetic method in time domain[J]. Chinese Journal of Geophysics (in Chinese), 46(5):719-724. |
| [18] | Macnae J, King A, Stolz N, et al. 1998. Fast AEM data processing and inversion[J]. Exploration Geophysics, 29(2):163-169. |
| [19] | Macnae J, Mortimer R, Gilgallon K. 2010. Deep conductor delineation through improved EMflow data processing[C].//21st Geophysical Conference, ASEG Extended Abstracts, 1-4. |
| [20] | Mao L F, Wang X B, Li W J. 2011. Research on 1D inversion method of fix-wing airborne transient electromagnetic record with flight altitude inversion simultaneously[J]. Chinese Journal of Geophysics (in Chinese), 54(8):2136-2147, doi:10.3969/j.issn.0001-5733.2011.08.021 |
| [21] | Meng Q M. 2004. The tentative application of integrated aerogeophysical survey to the prospecting for copper-polymetallic deposits in the forest and grassland region[J]. Geophysical and Geochemical Exploration (in Chinese), 28(4):333-340. |
| [22] | Nabighian M N. 1987. Electromagnetic Methods in Applied Geophysics[M]. Tulsa Oklahoma:Society of Exploration Geophysicists. |
| [23] | Palacky G J. 1993. Use of airborne electromagnetic methods for resource mapping[J]. Advances in Space Research, 13(11):5-14. |
| [24] | Piao H R. 1990. Electromagnetic Sounding Theory (in Chinese)[M]. Beijing:Geological Publishing House, 1-10. |
| [25] | Qiang J, Luo Y, Tang J, et al. 2010. The algorithm of all-time apparent resistivity for Airborne Transient Electromagnetic (ATEM) survey[J]. Progress in Geophys.(in Chinese), 25(5):1657-1661, doi:10.3969/j.issn.10042903.2010.05.018. |
| [26] | Raiche A. 2004. Practical 3D airborne EM inversion in complex terranes[C].//17th International Geophysical Conference and Exhibition, ASEG, Extended Abstracts. 1-4. |
| [27] | Sattel D. 2005. Inverting airborne electromagnetic (AEM) data with Zohdy's method[J]. Geophysics, 70(4):G77-G85. |
| [28] | Smith R. 2008. Various applications of applied controlled source airborne electromagnetic methods[C].//19th International Workshop on Electromagnetic Induction in the Earth, 379-384. |
| [29] | Vasterling M, B?rner R, Spitzer K. 2008. 1-D Inversion of Airborne Electromagnetic Data From 2-D and 3-D Models[C].//19th EM Workshop, Beijing, China. |
| [30] | Viezzoli A, Christiansen A V, Auken E, et al. 2008. Quasi-3D modeling of airborne TEM data by spatially constrained inversion[J]. Geophysics, 73(3):F105-F113. |
| [31] | Wang W P, Wang Y S. 1999. The application of airborne electromagnetic method to the exploration of shallow fresh water at the mouth area of the Yellow River[J]. Geophysical and Geochemical Exploration (in Chinese), 23(2):115-121. |
| [32] | Wolfgram P, Karlik G. 1995. Conductivity-depth transform of GEOTEM data[J]. Exploration Geophysics, 26(3):179-185. |
| [33] | Wolfgram P, Sattel D, Christensen N B. 2003. Approximate 2D inversion of AEM data[J]. Exploration Geophysics, 34(2):29-33. |
| [34] | Yin C C, Huang W, Ben F. 2013. The full-time electromagnetic modeling for time-domain airborne electromagnetic systems[J]. Chinese J. Geophys.(in Chinese), 56(9):3153-3162, doi:10.6038/cj20130928. |
| [35] | Yin C C, Qi Y F, Liu Y H, et al. 2014. Trans-dimensional Bayesian inversion of frequency-domain airborne EM data[J]. Chinese J. Geohphys. (in Chinese), 57(9):2971-1980, doi:10.6038/cjg20140922. |
| [36] | Zhdanov M S, Pavlov D A, Ellis R G. 2002. Localized S-inversion of time-domain electromagnetic data[J]. Geophysics, 67(4):1115-1125. |
| [37] | Zhu K G, Lin J, Liu C S, et al. 2008. One-dimensional forwand and prospecting depth for airborne frequency domain electromagnetic method[J]. Progress in Geophysics (in Chinese), 23(6):1943-1946. |
| [38] | Zhu K G, Lin J, Han Y H, et al. 2010. Research on conductivity depth imaging of time domain helicopter-borne electromagnetic data based on neural network[J]. Chinese Journal of Geophysics (in Chinese), 53(3):743-750, doi:10.3969/j.issn.00015733.2010.03.03. |
| [39] | 陈小红,段奶军. 2012.时间域航空电磁快速成像研究[J].地球物理学进展, 27(5):2123-2127, doi:10.6038/j.issn.1004-2903.2012.05.037. |
| [40] | 方文藻,李予国,李貅. 1993.瞬变电磁测深法原理[M].西安:西北工业大学出版社, 66-68. |
| [41] | 李貅. 2002.瞬变电磁测深原理的理论与应用[M].西安:陕西科学技术出版社. |
| [42] | 李貅,全红娟,许阿祥,等. 2003.瞬变电磁测深的微分电导成像[J].煤田地质与勘探, 31(3):59-61. |
| [43] | 李永兴,强建科,汤井田. 2010.航空瞬变电磁法一维正反演研究[J].地球物理学报, 53(3):751-759, doi:10.3969/j.issn.00015733.2010.03031. |
| [44] | 罗延钟,张胜业,王卫平. 2003.时间域航空电磁法一维正演研究[J].地球物理学报, 46(5):719-724. |
| [45] | 毛立峰,王绪本,陈斌. 2011.直升机航空瞬变电磁自适应正则化一维反演方法研究[J].地球物理学进展, 26(1):300-305. doi:10.3969/j.issn.10042903.2011.01.035. |
| [46] | 孟庆敏. 2001.航空物探综合测量在森林和草原区寻找铜多金属矿的试验研究[J].物探与化探, 28(4):333-340. |
| [47] | 朴化荣. 1990.电磁测深原理[M].北京:地质出版社, 1-10. |
| [48] | 强建科,罗延钟,汤井田,等. 2010.航空瞬变电磁法的全时域视电阻率计算方法[J].地球物理学进展, 25(5):1657-1661, doi:10.3969/j.issn.10042903.2010.05.018. |
| [49] | 殷长春,黄威,贲放. 2013.时间域航空电磁系统瞬变全时响应正演模拟[J].地球物理学报, 56(9):3153-3162, doi:10.6038/cj20130928. |
| [50] | 殷长春,齐彦福,刘云鹤,等. 2014.频率域航空电磁数据变维数贝叶斯反演研究[J].地球物理学报, 57(9):29712980, doi:10.6038/cjg20140922. |
| [51] | 朱凯光,林君,刘长胜,等. 2008.频率域航空电磁法一维正演与探测深度[J].地球物理学进展, 23(6):1943-1946. |
| [52] | 朱凯光,林君,韩悦慧,等. 2010.基于神经网络的时间域直升机电磁数据电导率深度成像[J].地球物理学报, 53(3):743-750, doi:10.3969/j.issn.00015733.2010.03.03. |
 2015, Vol. 30
2015, Vol. 30


