2. 中国地质大学 工程技术学院, 北京 100083
2. China University of Geosciences, School of Engineering and Technology, Beijing 100083, China
岩体中结构面的力学性质非常复杂,影响应力波在结构面的传播因素众多,如结构面形貌、厚度、力学特性、结构面间距和应力波频率等.用准静态共振柱试验表明:岩体结构面表明的粗糙度、波浪起伏及接触特性对长波长P波和SV波的传播速度及波峰到波谷的高度有明显影响,总的来说,粗糙度系数(JRC)增加,SV波速度增加,而P波速度和剪切波阻尼比减小(Mohd-Nordin et al.,2014),因此建立理论模型需进行一定简化.
夹层是岩体中具有一定厚度的结构面,当夹层厚度较小时,不考虑夹层质量,假设结构面是平直的,采用弹簧模型描述夹层的变形特性,在线弹性位移不连续理论基础上,Pyrak-Nolte(Pyrak-Nolte,1996)推导出应力波在结构面的透射系数和反射系数的解析解.应力波在结构面传播过程可以在频域中进行,也可以在时域中进行,Li(Li et al.,2012)假设岩体结构面满足线弹性变形,根据位移不连续模型和时间位移函数,基于波阵面处动量守恒提出了应力波通过线性结构面的波动方程,采用差分法计算应力波传过结构面的时域波形.大量研究表明结构面变形过程通常是非线性的,大振幅应力波传播或结构面刚度较低时非线性变形表现得更为突出,线性变形是对非线性变形的简化.王卫华等(王卫华等,2006)通过分析应力波与张开节理相互作用过程,建立了非线性位移不连续解析模型,研究了不同应力波在张开节理处的能量传递规律,俞缙(俞缙等,2012)进一步不同应力波穿过多条非线性变形节理时的透射特性,研究表明,随着节理条数的增加,速度和能量透射系数逐渐降低,高谐波频域幅值先增大后下降,时间延迟增大的速度逐渐加快.由于层状岩体的普遍性,工程中应力波传过一组结构面时经常会遇到问题,结构面的间距与波长之比是影响应力波传过一组结构面的重要因素,Cai(Cai and Zhao,2000)基于特征线法,提出钻石型特征线模型,对弹性 P 波法向入射一组平行线弹性变形节理时的传播进行了初步分析,确定了节理间距影响透射系数的 2 个门槛值,并将节理间距分成 3个区间,不同区间内透射系数有不同的变化规律.随后,Zhao等(Zhao et al.,2006)改进了钻石型特征线模型,提出修正钻石型特征线模型,研究垂直穿越非线性变形单组节理的弹性 P 波传播规律.
当结构面厚度达到一定值时,且夹层充填物的变形参数较小时,结构面往往表现为弱连接,尹尚先(尹尚先等,2007)用柔度系数表征弱连接界面,研究不连续界面的透、反射系数与时间延迟和频率的关系.当夹层厚度与应力波波长可以相比拟时,忽略夹层内部反射波的波传播模型不再成立,范留明(范留明等,2006)假设应力波在软弱夹层内发生一重反射,讨论了单个具有一定厚度的结构面的动力响应及振幅衰减特性.范留明的研究只考虑一重反射,当结构面厚度或间距与波长之比较小时,多重反射的作用表现得尤为突出(胡世丽等,2011).针对这个问题,罗松南将软弱夹层看成非均匀损伤带,根据损伤带两侧的总位移场、应力连续和位移连续条件,建立了考虑应力波在软弱夹层内的多重透反射时的透射系数和反射系数计算公式(罗松南等,2006).该模型采用第一、第二类Legendre多项式算法,则多项式中n要求必须为正整数,算法上会造成应力波频率在较大范围内变化时透射系数几乎不变,即透射系数对频率不敏感.为提高透射系数对频率的敏感性,本文采用Legendre方程的级数解法计算透射系数,研究软弱夹层透射系数的实部、虚部和子波传过软弱夹层的波形变化规律.
1 应力波在软弱夹层的传播模型设软弱夹层为损伤材料,设损伤度为

式中E为材料损伤后的弹性模量,E0为材料损伤前的弹性模量,D为损伤度.
由式(1)得损伤后材料的弹性模量为

一维含软弱夹层岩体模型,如图 1所示,x<x1的区域为介质1,x>x2的区域为介质3,介质1和介质3为均匀损伤区域,损伤度分别为D1和D3;x1<x<x2的区域为软弱夹层,软弱夹层的损伤度函数为D(x);在分界面x=x1和x=x2处损伤度连续、导数不连续.含软弱夹层岩体的损伤度函数为
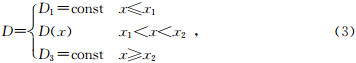
式中x为位置坐标,D1和D3分别为介质1和介质3的损伤度.
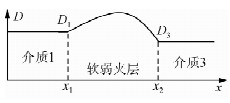 | 图 1 含软弱夹层的岩体模型Fig. 1 Rock mass model containing soft interlayer |
考虑应力波传过软弱夹层为一维问题,其波动方程为

式中 u为位移,ρ为密度,E为弹性模量.
式(4)为二阶微分方程,其解的一般形式可表示为
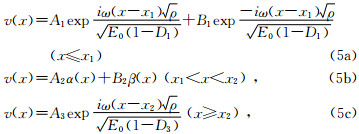
式中A1,A3分别表示波在介质1和介质3中右行波的振幅,B1表示波在介质1中左行波的振幅,A2,B2为未知常数,α(x)、β(x)表示在区域x1<x<x2内的两个线性无关解.
若采用第一、第二类Legendre多项式算法(罗松南等,2006),则透射系数对频率变化不敏感.为提高透射系数的计算精度,采用Legendre方程的级数解来确定α(x)、β(x),求得:
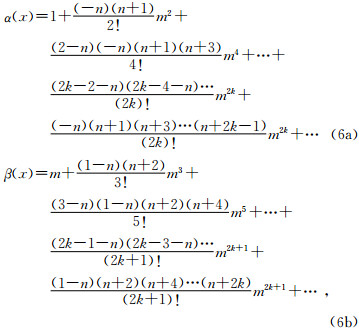
式中k为正整数.
假设应力波传过软弱夹层时,在界面x=x1处位移连续、应力连续可得:
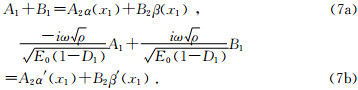
同理在x=x2处位移连续、应力连续可得:
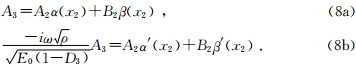
透射系数为

当给定入射波频率ω和介质的物理力学参数,联解式(7)和式(8)求得透射系数T.
2 透射系数的变化规律设在介质1中输入一列简谐波,简谐波向右传播传过软弱夹层后进入介质3中,入射的简谐波为

假设软弱夹层的损伤度函数D(x)为二次曲线,当入射波的振源与软弱夹层的距离为0.1 m,损伤度函数为
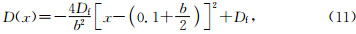
式中Df和b分别为软弱夹层的峰值损伤度和厚度.
设介质1和介质3的弹性模量E=20 GPa,损伤度D1=D3=0,介质密度ρ=2500 kg/m3.软弱夹层的厚度b=0.1 m,入射波频率分别取200 Hz,800 Hz,1500 Hz,运用前述应力波在软弱夹层的传播模型,计算得到透射系数实 部TR和虚部TI与峰值损伤度Df的关系,如图 2所示.从图 2(a)可以看出,存在一个临界峰值损伤度Dcri-r,当损伤度小于Dcri-r时,透射系数的实部基本不受损伤度的影响,即透射系数的实部不能反映损伤度变化;当损伤度大于Dcri-r时,随损伤度的增加,透射系数的实部快速减小至0;随频率增加,临界峰值损伤度Dcri-r减小.从图 2(b)得出:透射系数的虚部也存在一个临界峰值损伤度Dcri-i,当损伤度小于Dcri-i时,随损伤度增加,透射系数的虚部增加;当损伤度大于Dcri-i时,随损伤度的增加,透射系数的虚部减小;随频率增加,临界峰值损伤度Dcri-i减小.从以上分析可以得出,如果根据振幅的变化反分析软弱夹层的峰值损伤度,则存在“盲区”,对于厚度为0.1 m的软弱夹层,频率为1500 Hz的谐波几乎能完全通过峰值损伤度小于0.6的软弱夹层,当峰值损伤度大于0.8时,该谐波几乎不能通过软弱夹层,即频率为1500 Hz的谐波只能反映峰值损伤度大于0.6且小于0.8的软弱夹层.由于振幅和相位存在互补性,而且引起相位变化的损伤度范围更大,波形能够综合反映振幅和相位,因而波形变化能够比振幅或相位更全面反映软弱夹层的力学参数.
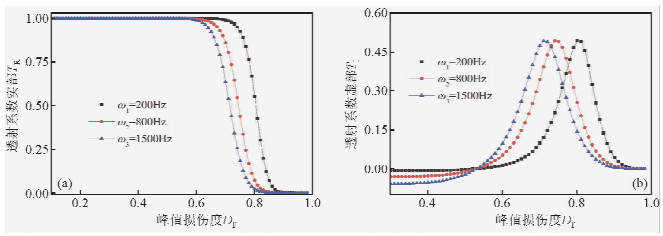 | 图 2 软弱夹层的峰值损伤度和频率对透射系数的影响Fig. 2 The influence of peak damage degree of soft interlayer and frequency on transmission coefficient |
当入射波频率ω=800 Hz,软弱夹层的厚度b分别为0.2 m、0.5 m和0.8 m,求得透射系数与峰值损伤度的关系,如图 3所示.从图 3可以得出,软弱夹层厚度对透射系数有明显影响,随软弱夹层厚度增加,透射系数的实部对应的临界峰值损伤度Dcri-r和虚部对应的临界峰值损伤度Dcri-i都减小.
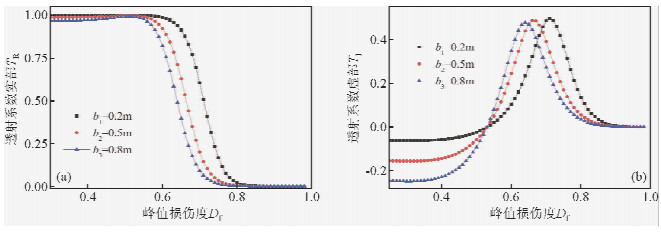 | 图 3 软弱夹层的厚度和峰值损伤度对透射系数的影响Fig. 3 The influence of peak damage degree and thickness of soft interlayer on transmission coefficient |
采用非均匀损伤介质描述软弱夹层,考虑了应力波在软弱夹层内的多重透射和反射,厚度和阻抗比是影响多重透射波和反射波叠加效应的一个主要因素.为研究叠加效应对透射系数的影响,定义一个无量纲量γ:

式中λ表示入射波波长.设介质1和介质3的损伤度为0,即D1=D3=0,根据波速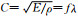 得:
得:

式中f为频率,ω=2πf.
定义阻抗比ζ:

式中 Z1、Zs分别表示介质1和软弱夹层的波阻抗,本文是研究软弱夹层对子波波形变化的影响规律,为计算简单,直接采用软弱夹层的峰值损伤度计算其波速,假设软弱夹层的密度与介质1的密度相同,由式(14)计算得:

运用应力波在软弱夹层的传播模型计算得到阻抗比与透射系数的关系,如图 4所示.由图 4a可知:当波长与厚度之比较小(如γ=0.25)时,随阻抗比的增加,透射系数的实部TR逐渐增加,最后趋近于0;当波长与厚度之比较大(如γ=1)时,随阻抗比的增加,透射系数的实部TR先缓慢减小,后快速减小,最后渐趋近于0,波长与厚度之比不同时,快速减小区间不同.由图 4b可知:当波长与厚度之比较小(如γ=0.25)时,随阻抗比的增加,透射系数的虚部TI逐渐增加,最后趋近于0;当波长与厚度之比较大(如γ=1)时,随阻抗比的增加,透射系数的虚部TI先增加,后快速减小,最后趋近于0,即透射系数的虚部TI存在一个峰值,波长与厚度之比不同时,峰值也不同.综合图 4表明,透射系数的相位比振幅的变化规律更丰富,波长与厚度之比不同时,透射系数的变化规律不同.
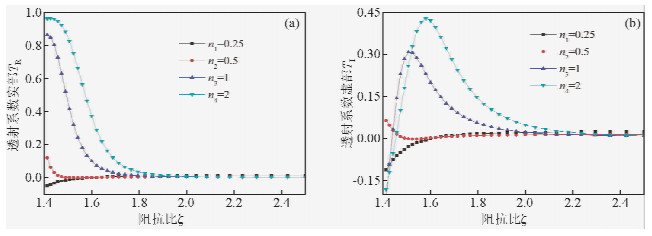 | 图 4 阻抗比对透射系数的影响Fig. 4 The influence of impedance ratio on transmission coefficient |
当入射波峰值频率为1000 Hz,波长与厚度比值对透射系数影响如图 5所示.由图 5可知:当峰值损伤度较小(如Df=0.6时),随着波长与厚度比值的增加,透射系数的实部TR和虚部TI先减小后增加,如峰值损伤度为0.6,当波长与厚度之比约为0.35时,透射系数实部TR和虚部TI达到最小值;当峰值损伤度较大时(如Df=0.8时),透射系数的实部TR和虚部TI逐渐减小.
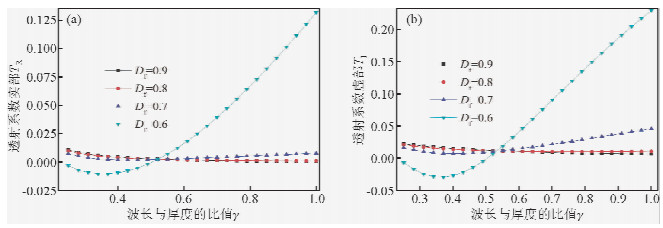 | 图 5 波长与厚度之比对透射系数的影响Fig. 5 The influence of ratio of wave length to thickness of soft interlayer on transmission coefficient |
上述研究表明,简谐波传过软弱夹层的相位变化比振幅变化更复杂,而相位对岩性和夹层的反演具有重要作用(赵军龙等,2010),在勘探资料处理中,相位差问题是影响反射信号实现同相叠加的重要因素之一(李振春等,2008),相位导数的平均值决定了时程峰值发生的大致时刻,相位导数的方差决定了强震段的持续时间(杨娜等,2012).由于确定子波相位比较困难,人们往往过分强调子波的振幅对反褶积质量的影响,而忽略子波相位的作用,在地震勘探资料的处理和解释过程中,对子波的相位特性,往往都需要有某种假设条件,而对高分辨率地震资料来说,这种前提条件的要求更为苛刻(李国发等,2005).
应力波传过软弱夹层后,振幅和相位都发生了变化,综合体现在波形的变化.子波具有良好的时-频局部化效果,能够明显提高分析结果的时间分辨率.现研究Ricker子波传过软弱夹层后的波形变化.Ricker子波在时间域里的表达式为(俞寿朋,1996)
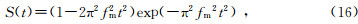
式中S(t)和fm分别为Ricker子波的振幅和峰值频率.
Ricker子波的频率域里的表达式为
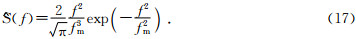
设软弱夹层的透射系数为

Ricker子波传过软弱夹层后的时域波形表达式为
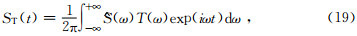
将式(18)代入式(19),计算得
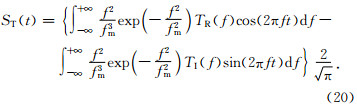
运用应力波在软弱夹层的传播模型计算得到透射系数,将计算所得的透射系数代入式(20),便可计算得Ricker子波传过软弱夹层的时域波形.
3.2 Ricker子波传过软弱夹层的波形变化分析峰值频率fm为1000Hz和振幅为1 cm的Ricker子波,分别传过峰值损伤度为0.5和0.7、厚度为0.2 m的软弱夹层后的时域波形,如图 6所示.从图 6可以看出,当峰值损伤度为0.7时,Ricker子波传过软弱夹层后,波形发生了很大变化,主要表现在主瓣不突出,波形在时域上表现得更平缓.
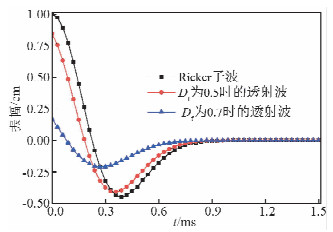 | 图 6 Ricker子波传过不同峰值损伤度软弱夹层的波形Fig. 6 The waveform of Ricker wavelet across different peak damage degree soft interlayer |
为进一步研究子波传过软弱夹层的波形变化,定义波形变化系数为
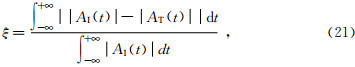
式中 AI(t)为入射波时域波形,AT(t)为透射波时域波形.
当软弱夹层峰值损伤度为0.7、厚度为0.5 m时,波形变化系数与Ricker子波峰值频率的变化关系如图 7所示.由图 7可得:不同峰值频率的Ricker子波传过软弱夹层时,波形变化系数随着峰值频率的增加而增加.
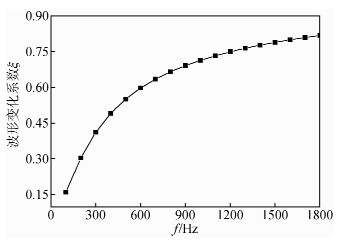 | 图 7 峰值频率对波形变化系数的影响Fig. 7 The influence of peak frequency on coefficient of waveform change |
当厚度为0.5 m,峰值频率分别为300 Hz、800 Hz、1500 Hz时,波形变化系数与峰值损伤度的关系如图 8所示.从图 8可以得出以下几点规律:
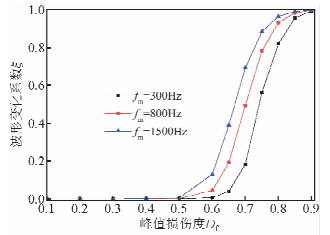 | 图 8 峰值损伤度和峰值频率对波形变化系数的影响Fig. 8 The influence of peak damage degree and peak frequency on coefficient of waveform change |
(1)波形变化系数曲线整体呈现S型,当峰值损伤度较小时,如峰值频率为300 Hz的Ricker子波,当峰值损伤度小于0.5时,波形变化系数曲线近似一条平稳直线,即透射波波形变化不明显;随着峰值损伤度的增加,波形变化系数曲线开始快速上升并渐趋于1,波形变化系数不断增大,与入射波波形相比较,透射波波形变化非常显著.
(2)不同峰值频率的子波受软弱夹层影响程度不同,如峰值频率为300 Hz的Ricker子波传过峰值损伤度为0.7的软弱夹层,波形变化系数为0.18,而峰值频率为3000 Hz的Ricker子波的波形变化系数为0.69,定义波形变化敏感区间,设波形变化系数从0.1增加至1时对应的峰值损伤度区间为敏感区间,峰值频率为300 Hz、800 Hz和1500 Hz时波形变化对损伤度的敏感区间分别为[0.67,1]、[0.62,1]和[0.58,1],随峰值频率增加,敏感区间的宽度增加,表明高频子波比低频子波能反映更大的损伤度范围.
(3)由不同峰值频率下的敏感区间对比可知,随着峰值频率的增加,波形变化系数敏感区间下限减小,敏感区间增加,说明高频子波可以用来探测损伤度较小的软弱夹层.
设峰值频率fm=2000 Hz,软弱夹层厚度分别为0.2 m、0.6 m、0.8 m,计算得到波形变化系数与峰值损伤度的关系,如图 9所示,基于前述方法计算波形变化系数对峰值损伤度的敏感区间,对于厚度为0.2 m软弱夹层,波形变化对峰值损伤度敏感的区间为[0.63,1];厚度为0.6 m时,波形变化对峰值损伤度敏感的区间为[0.55,1];厚度为0.8 m时,波形变化对峰值损伤度敏感的区间为[0.51,0.9].不同厚度下的敏感区间对比可知,随着厚度的增加,波形变化系数敏感区间下限减小,敏感区间宽度增加,说明:软弱夹层的厚度越大,基于波形变化反分析其力学参数越容易.
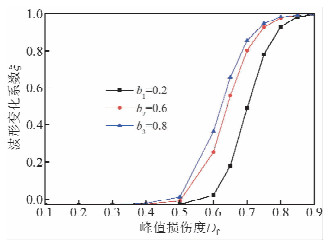 | 图 9 峰值损伤度和厚度对波形变化系数的影响Fig. 9 The influence of peak damage degree and thickness of soft interlayer on coefficientof waveform change |
在德兴铜矿露天开采临时边坡面上选择一软弱夹层,该夹层上下台阶宽度大于50 m,边坡角为70°,夹层厚度为0.42 m,其两侧岩体相对完整,岩性相同.如图 10所示,在垂直软弱夹层方向布置1条测线,沿测线方向在夹层两侧各布置1测点,用石膏粉将加速度传感器粘结在测点上,传感器x方向与测线方向一致.在测线上选定一振源点(施加冲击荷载),振源点所在的一侧为入射侧,另一侧为透射侧,测点1位于入射侧,测点2位于透射侧,测点1、软弱夹层左边界和测点2与振源点的距离分别为0.44 m、0.58 m和1.08 m.传感器参数为:电荷灵敏度范围为10.284~14.147 pC/(ms-2),频响为0.2 Hz~5 kHz.施加一个冲击荷载,测点的振动信号经传感器拾振,由电荷滤波积分放大器处理,电荷滤波积分放大器设置为低通3 kHz,单通道采样率为15 kHz,采用北京东方振动与噪声技术研究所产生的INV306振动采集仪记录测点振动波形.
在试验区域选择典型岩块,加工成标准岩样,采用常规方法测试得岩块的密度为2520 kg/m3,泊松比为0.22.采用中国科学院武汉岩土力学研究所研制的GY-90钻孔弹模仪测试软弱夹层两侧岩体的弹性模量,测试结果为13.4 GPa.
 | 图 10 子波波形变化测试现场Fig. 10 The test field of waveform change of wavelet |
图 10所示测点2右侧为半无限延伸均质体,相应传感器记录的振动波形为实测透射波,测点1为入射侧,其传感器记录的波形为入射侧实测波形,包含有入射波和反射波.以透射波计算入射侧波形,当入射侧的计算波形和实测波形差异最小时,确定该软弱夹层峰值损伤度为0.84.
4.2 子波传过软弱夹层的波形变化规律以实测透射子波计算入射子波,步骤为:(1)对实测透射
波进行带通滤波得到透射子波,带宽为100 Hz;(2)对不同频率范围内透射子波进行傅里叶变换,得实测透射子波的频谱;(3)软弱夹层峰值损伤度为0.84,分别计算子波在软弱夹层的透射系数和反射系数;(4)对实测透射子波的频谱除以透射系数,得到计算入射子波的频谱;(5)对计算入射子波的频谱进行傅里叶逆变换,得到计算入射子波波形.
采用波形变化系数量化入射子波与透射子波的波形差异,量化公式见式(21),得子波波形变化系数与子波主频的关系,见图 11.由图 11可得:实测子波波形变化系数随子波主频的增加而增加,这一变化趋势与理论Ricker子波传过软弱夹层的波形变化变化规律一致.
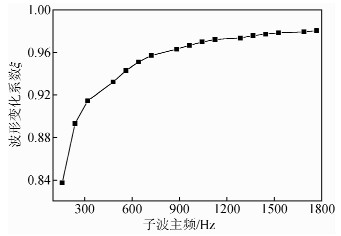 | 图 11 子波主频对波形变化系数的影响Fig. 11 The influence of peak frequency on coefficient of the dominant frequency |
将岩体软弱夹层抽象为损伤度按照二次曲线变化的损伤介质,采用Legendre方程的级数法求解应力波传过软弱夹层的透射系数,研究了软弱夹层的厚度、峰值损伤度和阻抗比对透射系数的影响,在此基础上,定义波形变化系数,分析了Ricker子波传过软弱夹层的波形变化规律,得出如下几点结论.
5.1 透射系数实部和虚部对损伤度变化表现出不同的变化规律,软弱夹层的损伤度较小时,透射系数实部随峰值损伤度增加几乎不变,即透射系数的实部不能反映损伤度变化,当损伤度大于临界峰值损伤度Dcri-r时,随损伤度增加,透射系数的实部快速减小至0;随频率和软弱夹层厚度增加,临界峰值损伤度Dcri-r减小.透射系数的虚部也对应一个临界峰值损伤度Dcri-i,当损伤度小于Dcri-i时,随损伤度增加,透射系数虚部增加;当损伤度大于Dcri-i时,随损伤度的增加,透射系数的虚部减小;随频率和软弱夹层厚度增加,临界峰值损伤度Dcri-i减小.振幅和相位在反映软弱夹层的几何和力学参数变化方面存在互补性,而且相位变化能够反映更大范围的损伤度变化,而波形能够综合反映振幅和相位,所以波形变化能够比振幅或相位更全面反映软弱夹层的力学参数.
5.2 当波长与厚度之比较小(如γ=0.25)时,随阻抗比的增加,透射系数的实部TR和虚部TI逐渐增加,最后趋近于0.当波长与厚度之比较大(如γ=1)时,随阻抗比的增加,透射系数实部TR先缓慢减小,后快速减小,最后趋近于0,波长与厚度之比不同时,快速减小区间不同;随阻抗比的增加,透射系数的虚部TI先增加,后快速减小,最后渐趋近于0,即透射系数的虚部TI存在一个峰值,波长与厚度之比不同时,峰值也不同.
5.3 Ricker子波传过软弱夹层后,不仅振幅发生衰减,相位也发生变化,由于两者对软弱夹层峰值损伤度的敏感区间不同,波形综合反映了振幅和相位的变化,因而能全面反映软弱夹层的力学特性.随损伤度增加,波形变化系数曲线整体呈现S型增加,波形变化系数对软弱夹层的峰值损伤度变化存在一个敏感区间,当峰值损伤度小于敏感区间的下限时,波形变化系数曲线近似一条平稳直线,说明波形变化不能反映软弱夹层的力学参数变化;高频子波比低频子波对软弱夹层的峰值损伤度敏感区间大;厚度越大,波形变化系数也越大,子波对软弱夹层峰值损伤度的敏感区间宽度也越大.
5.4 以实测透射子波计算入射子波,采用波形变化系数量化二者差异,现场试验子波波形变化系数随主频的增加而增加;理论计算Ricker子波传过软弱夹层时,峰值频率增加,波形变化系数增加;理论推导与试验结果变化规律一致.
致 谢 感谢审稿专家提出的修改意见和编辑部的大力支持!
| [1] | Cai J G, Zhao J. 2000. Effects of multiple parallel fractures on apparent attenuation of stress waves in rock masses[J]. International Journal of Rock Mechanics and Mining Sciences, 37(4):661-682. |
| [2] | Fan L M, Yan N, Li N. 2006. Dynamic response model for thin soft interlayer considering interbedded reflecting waves[J]. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 25(1):88-92. |
| [3] | Hu S L, Luo S H, Wang G S. 2011. Influence of structural face interval on transmission wave[J]. Mining and Metallurgical Engineering (in Chinese), 31(4):5-8. |
| [4] | Li G F, Mu Y G, Wang P. 2005. A interactive technique for seismic wavelet extraction[J]. Journal of the University of Petroleum, China (in Chinese), 29(5):33-36. |
| [5] | Li J C, Li H B, Ma G W, et al. 2012. A time-domain recursive method to analyse transient wave propagation across rock joints[J]. Geophysical Journal International, 188(2):631-644. |
| [6] | Li Z C, Wang X P, Han W G. 2008. Review of phase correction in seismic data processing[J]. Progress in Geophysics (in Chinese), 23(3):768-774. |
| [7] | Luo S N, Zhou Z P, Tong H. 2006. Wave propagation in an inhomogeneous damaged zone[J]. Journal of Vibration and Shock (in Chinese), 25(5):74-76, 80. |
| [8] | Mohd-Nordin MM, Song K, Cho GC, et al. 2014. Long-wavelength elastic wave propagation across naturally fractured rock masses[J]. Rock Mechanics and Rock Engineering, 47(2):561-573. |
| [9] | Pyrak-Nolte L J. 1996. Seismic response of fractures and the interrelations among fractures[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 33(8):787-802. |
| [10] | Wang W H, Li X B, Zuo Y J. 2006. Effects of single joint with nonlinear normal deformation on p-wave propagation[J]. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 25(6):1218-1225. |
| [11] | Yan N, Tian Y J, Yang Q S. 2012. Artificial ground motions correlated to a specified earthquake record[J]. Journal of Vibration and Shock (in Chinese), 31(19):36-39. |
| [12] | Yin S X, Wang S X, Wei J X, et al. 2007. The propagating rule study on elastic wave across loosely-boned interface[J]. Journal of Basic Science and Engineering (in Chinese), 15(3):317-331. |
| [13] | Yu J, Qian Q H, Song B X, et al. 2012. Transmission of various stress waves across multi-fracture with nonlinear deformation behavior[J]. Engineering Mechanics (in Chinese), 29(4):1-6. |
| [14] | Yu S P. 1996. Wide band Ricker wavelet[J]. OGP (in Chinese), 31(5):605-615. |
| [15] | Zhao J L, Li X S, Zhang B. 2010. New fluid detection method based on well logging curve wavelet analysis and Hilbert Transform[J]. Oil Geophysical Prospecting (in Chinese), 45(2):290-294, 305. |
| [16] | Zhao X B, Zhao J, Cai J G. 2006. P-wave transmission across fractures with nonlinear deformational behaviour[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 30(11):1097-1112. |
| [17] | 范留明,闫娜,李宁. 2006.薄弹性软弱夹层的动力响应模型[J].岩石力学与工程学报, 25(1):88-92. |
| [18] | 胡世丽,罗嗣海,王观石. 2011.结构面间距对透射波的影响[J].矿冶工程, 31(4):5-8. |
| [19] | 李国发,牟永光,王濮. 2005.交互地震子波提取技术[J].石油大学学报(自然科学版), 29(5):33-36. |
| [20] | 李振春,王希萍,韩文功. 2008.地震数据处理中的相位校正技术综述[J].地球物理学进展, 23(3):768-774. |
| [21] | 罗松南,周正平,童桦. 2006.具有非均匀损伤带状区域中波的传播[J].振动与冲击, 25(5):74-76, 80 |
| [22] | 王卫华,李夕兵,左宇军. 2006.非线性法向变形节理对弹性纵波传播的影响[J].岩石力学与工程学报, 25(6):1218-1225. |
| [23] | 杨娜,田玉基,杨庆山. 2012.与指定地震记录相关的非平稳地震动场的模拟[J].振动与冲击, 31(19):36-39. |
| [24] | 尹尚先,王尚旭,魏建新,等. 2007.弱连接界面弹性波波动规律研究[J].应用基础与工程科学学报, 15(3):317-331. |
| [25] | 俞缙,钱七虎,宋博学,等. 2012.不同应力波穿过多条非线性变形节理时的透射特性[J].工程力学, 29(4):1-6. |
| [26] | 俞寿朋. 1996.宽带Ricker子波[J].石油地球物理勘探, 31(5):605-615. |
| [27] | 赵军龙,李新胜,张彬. 2010.基于测井曲线小波分析与希尔伯特变换的流体识别新方法[J].石油地球物理勘探, 45(2):290-294, 305. |
 2015, Vol. 30
2015, Vol. 30

