2. 中国石油大学(北京)地球物理与信息工程学院, 北京 102249;
3. 中国石油集团测井有限公司生产测井中心, 西安 710201
2. College of Geophysics and Information Engineering, China University of Petroleum, Beijing 102249, China;
3. Production Logging Center of China Petroleum Logging CO. LTD., Xi'an 710201, China
经过长时间的注水驱油开发后,我国很多油田进入了高含水采油期,为了实现油田的稳产挖潜,确定剩余油分布以及注水前沿成为生产实践中亟待解决的问题.井-地电位测量技术利用开发井的钢套管作电极向井下供入大功率直流电流,在地表测量由地下介质的电性变化形成的电位分布,进而计算地下介质的电阻率分布.井地电位测量系统如图 1.由于供电套管直径远小于套管长度,故可以将套管简化为有限长线电流源来处理.若介质是均匀的,在直线电极到达的深度范围内,电流密度是上下一致的,从而克服了惯用的点源电法的电流密度随深度增加而迅速下降的缺点(李心刚,1986).井地电位法具有对地层影响小、对电阻率分布敏感、测量成本低的优点,这使得井地电位法逐渐成为研究剩余油分布、注水驱油前沿探测等问题的重要手段(朱涛等,2008).
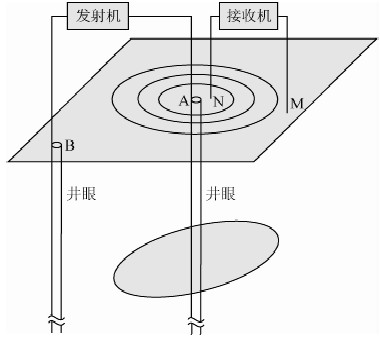 | 图 1 井地电位测量系统示意图 Fig. 1 Schematic diagram of borehole-to-surface electric potential measurement system |
很多专家学者对井地电位进行了理论和应用研究.国外,Mizunaga和Ushijima(1991),Mizunaga等(2003)利用有限差分方法实现了垂直线源和倾斜线源的三维井地电位正反演,国内很多相关数值模拟研究也是基于该正反演方法展开的.Ushijima等(1999)描述了该法在储层流体监测方面的应用.Aono(2003)等讨论了基于三维井地电阻率成像的4D裂缝监测.Ho(2009)采用神经网络实现了三维井地电位的快速反演.国内,徐凯军和李桐林(2006)采用有限差分法对垂直线源三维井地电位法进行了正演研究.刘地渊等(2006)对任意线源三维井地电位法进行了正演研究.李长伟等(2010)基于点源场方法实现了井地电位测量的三维正演计算.刘海飞等(2011),实现了连续介质三维线源井地电位正演计算.戴前伟等(2012)利用有限元法对复杂管网线源井地电位系统进行了正演模拟.朱凯光等(2013)研究了井地电法的电阻率和极化率双参数联合监测的有效性.本文在前人的研究基础上,推导了正常电位解析式及相应的装置系数和边界条件公式,并对比研究了不同的公式对正演数值模拟结果造成的影响.
1 井地电位测量系统正演理论井地电位测量系统的正演是指已知井周围地层介质的电阻率参数分布,计算出测量系统地表的电位分布,为现场测量数据的反演和解释奠定基础.
1.1 线电源场的基本分析方法在井地电阻率法中,所得的观测数据是地表的电位数据.为消除源点附近的奇异性,提高三维正演的计算精度,目前一般采用奇异点分离法,即将总电位分离成背景电位和异常电位(徐世浙等,1994),表达式为

稳恒电流源供电下,总电位U满足以下泊松方程

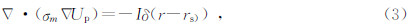
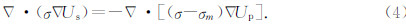
在利用有限差分进行电法勘探正演计算时,还需要设置所处理问题的边界条件进而求解.井地电位中的边界条件主要包括以下两种:
(1)在地面边界上,由于认为空气是绝缘体,选择使用诺依曼边界条件

(2)在无限远处边界面上,为了保持电位的物理特性,消除电性突变,选择使用混合边界条件


利用有限差分法,对上述偏微分方程(4-7)进行离散化处理,建立大型稀疏线性方程组AUs=S(A为容量矩阵,S为右端项),其中稀疏矩阵采用一维压缩存储技术进行存储,再利用稳定双共轭梯度算法(BICGSTAB)实现线性方程组的快速求解(Van der Vorst,1992),计算出异常电位Us,最后再与正常电位Up叠加,便可得到总电位U.
2 均匀介质中线电流源的正常电位如图 2所示的均匀半空间,介质电阻率为ρ,地下线电流源AB在任意点P(xp,yp,zp)产生的电位为Up.对于Up的解析式,目前大多数中文文献,如文献(凌明友等,2003;谭河清等,2004;蔡圣权等,2005;李艾红等,2008;戴前伟等,2008;屈有恒,2008;徐晓会,2009;章钰,2009;马捷等,2010;幸娟,2010),采用了公式(8);柯敢攀和黄清华(2009)给出了公式(9);Mizunaga和Ushijima(1991)采用了公式(10),但式(10)只适合垂直线源顶面与地面接触的情况.而式(8-10)没有明显的相关性.为方便后续研究,本文根据位场理论中的“镜像法”,详细推导了有限长垂直线电流源在均匀半空间中任意位置时的正常电位的解析式: 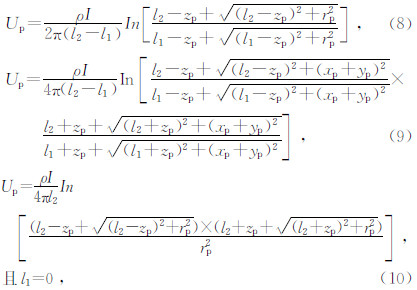
其中l1和l2分别为垂直线源的顶、底埋深,单位为m;zp为测点的埋深,单位为m;I为供电电流强度,单位为A;点P到垂直线源的径向距离为rp,单位为 m.
由“镜像法”,P点的电位可以由线源AB及其镜像A×B×上的点电流源产生的电位进行线积分得到式(11)(屈有恒,2008).
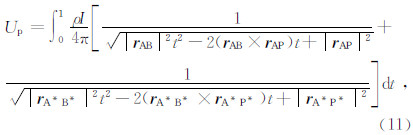
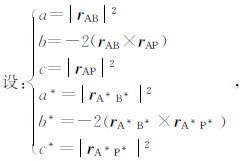
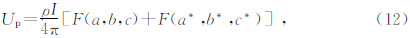
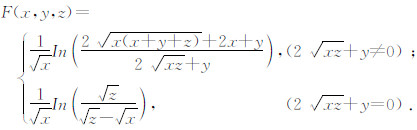
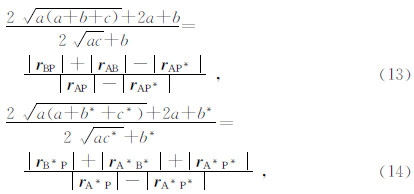
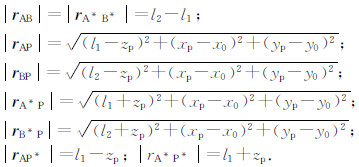
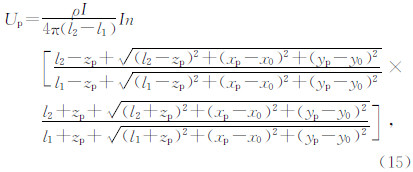
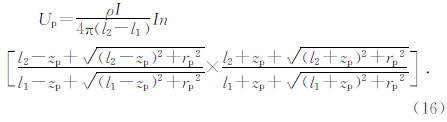
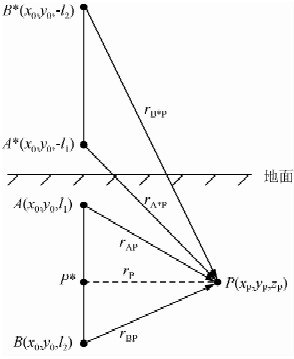 | 图 2 地下垂直线源在P点的电位计算示意图 Fig. 2 Schematic diagram of the electric potential at point P excited by the vertical current line source |
将垂直线源的顶端设置在地表,即l1=0,此时式(16)便可简化为式(10),式(16)是式(10)的一般表达式.式(8)比式(16)缺少了一项,式(9)对rp的计算有误.
3 正演数值模拟的混合边界条件对于无限远边界上任一点(xp,yp,zp),利用垂直有限线源的正常电位解析公式(16),通过对该式在x,y,z方向求导得到∂U/∂n,除以Up,便可推出系数λ的值.

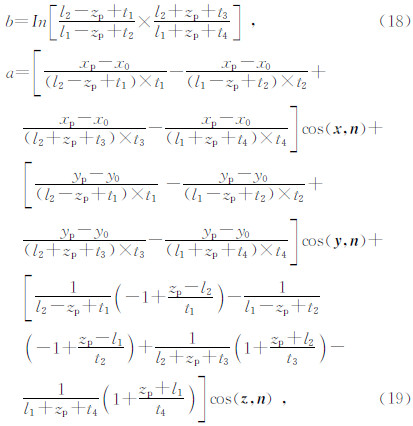
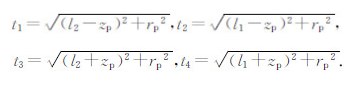
根据测量电极的排布方式的不同,井地电位电阻率测量装置可分为二极装置、三极装置和四极装置.
装置系数是一个仅与电极间空间位置有关的量,设n极装置的装置系数为Gn,已知测量电位(或总电位)U和充电电流I时,通过式(20)可计算视电阻率ρs,其单位为Ω·m,公式20为

在电阻率为ρ的均匀大地中的单一线电流源A极供电,M极观测,B极和N极位于无穷远处,距离井口2 km以外即视为无穷远.电位观测点M极位于地面,即zp=0,可推导出二极装置系数G2.设hAM和hAN分别是A电极与M、N电极之间的水平距离,hBM和hBN分别是B电极与M、N电极之间的水平距离,均匀介质中线电流源在M点产生的电位为
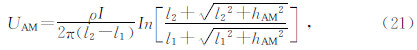

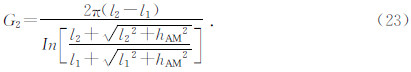
三级装置为供电电极A,以及测量电极M和N在测区内,B极仍然是位于无穷远的供电点电极.同上,可推导出三极装置系数G3的表达式为
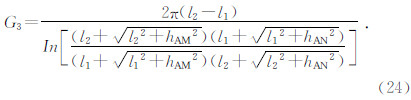
四极装置为供电电极A和B,以及测量电极M和N都在测区内.同上,可推导出四极装置系数G4的表达式为
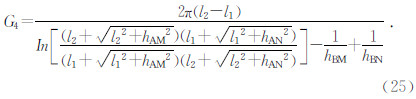
在均匀半空间中,已知顶端与地面接触时的垂直线源的解析式为公式(10),对式(8)、式(9)和式(16)在均匀半空间的电位响应进行对比分析,以说明这三个公式在数值上的区别以及所推导公式(16)的正确性.背景电阻率为100 Ω·m,线源长2000 m,在地层中深0 m(地表)和深200 m处电位随距线源的距离的变化如图 3和图 4所示.由图可知,总体上四条曲线逐渐减小的趋势都是一致的,在地表处,式(8)和式(16)与解析解的结果是一致的,而式(9)的结果偏小.在深200 m处,所推导公式(16)与解析式结果依然吻合,具有较高的准确度,式(8)的结果偏大,式(9)的结果偏小.当所处的深度越深,这种偏差变大.
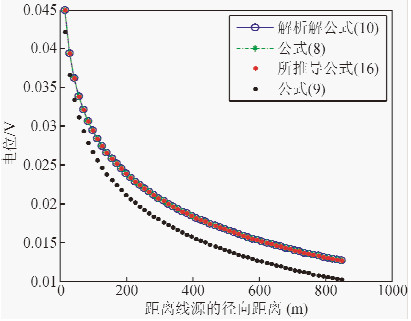 | 图 3 均匀半空间中地层中深0 m的电位(V)随距离线源的距离的变化分布 Fig. 3 Electric potential (V) at depth 0 m versus distance from the line source in the homogenous half space |
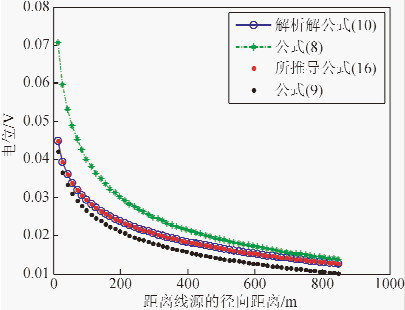 | 图 4 均匀半空间中地层中深200 m的电位(V)随距离线源的距离的变化分布 Fig. 4 Electric potential (V) at depth 200 m versus distance from the line source in the homogenous half space |
为了研究普遍使用的正常电位、混合边界条件和装置系数的计算公式和本文所推导的计算公式对非均匀地层的数值模拟结果的影响和差别,设计了两个高阻异常体模型和两个低阻异常体模型.供电电流均为+10 A,垂直套管的顶底埋深分别为10 m和350 m,四个模型中异常体大小和位置均相同,其顶底埋深分别为20 m和280 m,大小为16 m×21 m×260 m.高阻异常体和低阻异常体的电阻率分别为1000 Ω·m和0.5 Ω·m.背景电阻率为100 Ω·m.采用正常电位公式(8)、文献(屈有恒,2008)中的混合边界条件公式和装置系数,对高阻模型和低阻模型分别进行正演计算,数值模拟结果如图 5和图 7所示.采用本文推导的公式(16)~(20)和(23),对高阻模型和低阻模型分别进行正演计算,数值模拟结果如图 6和图 8所示.图(a)中xoy平面中央的空心圆表示井眼在水平面的投影,左上角红色区域表示高阻异常体在水平面的投影,蓝色区域表示低阻异常体在水平面的投影.
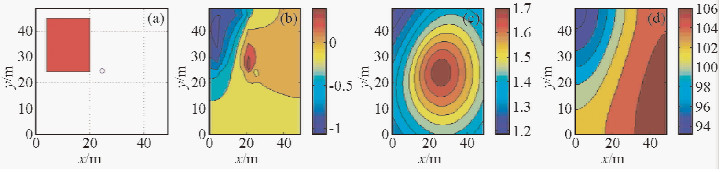 |
图 5 高阻模型一异常电位响应 (a)高阻异常体xoy平面分布;(b)100 m深处异常电位分布(V);(c)地表总电位分布(V);(d)视电阻率分布(Ω·m). Fig. 5 Abnormal potential response of the high resistive model 1 (a) High resistive anomaly on the xoy plan;(b) The abnormal potential distribution at depth 100m;(c) The total potential distribution on the surface;(d) Apparent resistivity distribution. |
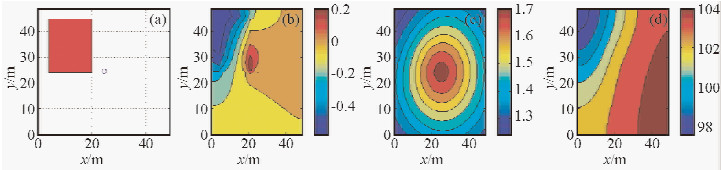 |
图 6 高阻模型二异常电位响应 (a)高阻异常体xoy平面分布;(b)100 m深处异常电位分布(V);(c)地表总电位分布(V);(d)视电阻率分布(Ω·m). Fig. 6 Abnormal potential response of the high resistive model 2 (a) High resistive anomaly on the xoy plan;(b) The abnormal potential distribution at depth 100 m;(c) The total potential distribution on the surface;(d) Apparent resistivity distribution. |
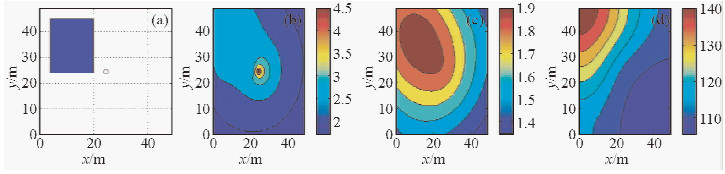 |
图 7 低阻模型一异常电位响应 (a)低阻异常体xoy平面分布;(b)100 m深处异常电位分布(V);(c)地表总电位分布(V);(d)视电阻率分布(Ω·m). Fig. 7 Abnormal potential response of the low resistive model 1 (a) Low resistive anomaly on the xoy plan;(b) The abnormal potential distribution at depth 100m;(c) The total potential distribution on the surface;(d) Apparent resistivity distribution. |
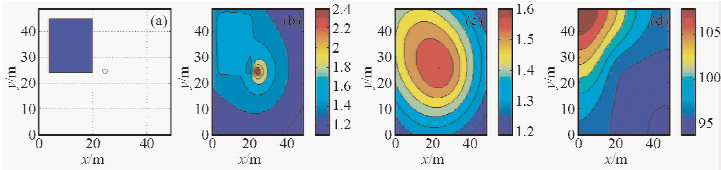 |
图 8 低阻模型二异常电位响应 (a)低阻异常体xoy平面分布;(b)100 m深处异常电位分布(V);(c)地表总电位分布(V);(d)视电阻率分布(Ω·m). Fig. 8 Abnormal potential response of the Low resistive model 2 (a) Low resistive anomaly on the xoy plan;(b) The abnormal potential distribution at depth 100 m;(c) The total potential distribution on the surface;(d) Apparent resistivity distribution. |
首先分析数值模拟结果中的相同点.在所设置的模型参数情况下,图 5和图 6表明,高阻异常体都引起了负异常电位响应,使得地表总电位等位线在异常体处呈压缩趋势,异常体在地面的投影都位于视电阻率图中的最大梯度带上.图 7和图 8表明,低阻异常体都引起了正异常电位响应,使得地表总电位等位线在异常体处呈拉伸趋势,异常体在地面的投影位于视电阻率图中的最大梯度带上.这一结果说明模型一和模型二都正确的模拟出了高阻异常体和低阻异常体的响应的一些特点. 然后,从异常电位响应的数值大小和分布范围上,可以看出文献(屈有恒,2008)中的公式和本文所推导的公式对异常体正演响应造成的差异,主要为图 6和图 8中电位和视电阻率的变化范围要比图 5和图 7中的小,当现场给定测量电位或者视电阻率时,反演出的地下不均匀介质电阻率对比度会比较大,利于现场数据解释.从图 7b和图 8b可以看出,对于低阻模型,二者异常电位分布差别相对较大,图 8b中的等位线分布与所设置低阻异常体(见图 7a)的边缘更吻合,更好地反映了低阻异常体边缘.图 7c中,低阻异常体对地表总电位等位线的拉伸效果较明显.
6 结论针对垂直有限长电流源的井地电位电阻率测量系统,本文对其正演模型进行了系统研究,详细推导了正演模型的正常电位的解析式,并且该解析式简化后(套管顶端与地面平行时)与Mizunaga和Ushijima(1991)中的解析式是一致的,进一步验证了本文所推公式的正确性.并在此基础上,推导了混合边界条件的解析式,以及常用的二极、三极、四极装置系数.通过对比数值模拟结果,表明对于均匀介质模型,本文模拟结果与解析结果相吻合,对于高阻异常体模型,公式(8)和本文推导的公式的仿真结果在异常响应的分布范围上较为一致,而对于低阻异常体模型,二者差异较大,本文的正演结果可以更准确地反映低阻异常体的边缘,更利于未来水驱前沿探测和剩余油分布的研究.
致 谢 感谢审稿专家和编辑部老师对本文的指导和帮助.| [1] | Aono T, Mizunaga H, Ushijima K. 2003. Imaging fractures during injection and production operation of reservoirs by a 4-D geoelectrical method[C].//Proceedings of the 6th SEGJ international Symposium. Tokyo. |
| [2] | Cai S Q, Ye Y P, Zou L X, et al. 2005. Application of well-ground potential image in residual oil evaluation of Wu1 block, Xinjiang Oilfield[J]. Special Oil and Gas Reservoirs (in Chinese), 12(5): 55-58, 65. |
| [3] | Dai Q W, Chen D P, Liu H F, et al. 2012. 3D FEM modelling of the borehole-to-surface potential method with complex pipe network linear current source[J]. Oil Geophysical Prospecting (in Chinese), 47(6): 998-1005. |
| [4] | Dai Q W, Chen D P, Xiong J K, et al. 2008. The 3-D finite element number modeling of vertical line source borehole ground DC method detecting underground dynamic conductor[J]. Chinese Journal of Engineering Geophysics (in Chinese), 5(6): 643-647. |
| [5] | Ho T L. 2009. 3-D inversion of borehole-to-surface electrical data using a back-propagation neural network[J]. Journal of Applied Geophysics, 68(4): 489-499. |
| [6] | Ke G P, Huang H Q. 2009. 3D forward and inversion problems of borehole-to-surface electrical method[J]. Acta Scientiarum Naturalium Universitatis Pekinensis (in Chinese), 45(2): 264-272. |
| [7] | Li A H, Su Y D, Wang H L, et al. 2008. Application of well-ground potential imaging technique in Shuanghe oil field[J]. Petroleum Geology and Engineering (in Chinese), 22(5): 78-80. |
| [8] | Li C W, Ruan B Y, Lü Y Z, et al. 2010. Three-dimensional FEM modeling of point source borehole-ground electrical potential measurements[J].Chinese J. Geophys. (in Chinese), 53(3): 729-736, doi: 10.3969/j.issn.0001-5733.2010.03.028. |
| [9] | Li X G. 1986. Discussion on vertical linear source resistivity method[J]. Oil Geophysical Prospecting (in Chinese), 21(2): 197-207. |
| [10] | Ling M Y, Hao X W, Cheng T J, et al. 2003. The study of remaining oil by the technic of well-earth electric potential image[J]. Fault-Block Oil & Gas Field (in Chinese), 10(4): 55-58. |
| [11] | Liu D Y, Xu K J, Zhao G M, et al. 2006. The study of three-dimensional geo-electric field of arbitrary shape line sources[J]. Progress in Geophys. (in Chinese), 21(2): 395-399, doi: 10.3969/j.issn.1004-2903.2006.02.010. |
| [12] | Liu H F, Chen D P, Dai Q W, et al. 2011. 3D FEM modeling of borehole-surface potential with line current source in semi-underground space of continuous variation of conductivity[J]. Journal of Guilin University of Technology (in Chinese), 31(1): 28-38. |
| [13] | Ma J, Feng D S, Liu H F, et al. 2010. Modeling and analysis for abnormal response on variable physical parameters by borehole-ground DC method[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 32(1): 1-5. |
| [14] | Mizunaga H, Aono T, Ushijima K. 2003. Three-dimensional inversion of the mise-à-la-masse data using a directional borehold[J]. BUTSURI-TANSA (in Japanese), 56(4): 209-218. |
| [15] | Mizunaga H, Ushijima K. 1991. Three-dimentional numerical modeling for the mise-à-la-masse method[J]. BUTSURI-TANSA (in Japanese), 44(4): 215-226. |
| [16] | Qu Y H. 2008. The 3-D numerical simulation and inversion for borehole-to-ground resistivity survey and dual frequency induced polarization (in Chinese)[Ph. D. thesis]. Beijing: China University of Geosciences. |
| [17] | Tan H Q, Shen J S, Zhou C, et al. 2004. Borehole-to-surface electrical imaging technique and its application to residual oil distribution analysis of the eighth section in Gudong Oilfield[J]. Journal of the University of Petroleum, China (in Chinese), 28(2): 31-37. |
| [18] | Ushijima K, Mizunaga H, Tanaka T. 1999. Reservoir monitoring by a 4-D electrical technique[J]. The Leading Edge, 18(12): 1422-1424. |
| [19] | Van der Vorst H A. 1992. Bi-CGSTAB: A fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems[J]. SIAM Journal on Scientific and Statistical Computing, 13(2): 631-644. |
| [20] | Xing J. 2010. Research on 3-D multi-parameter borehole-ground electrical numerical simulation and contrast (in Chinese)[Master thesis]. Changchun: Jilin University. |
| [21] | Xu K J, Li T L. 2006. The forward modeling of three-dimensional geoelectric field of vertical finite line source by finite-difference method[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 36(1): 137-141. |
| [22] | Xu S Z, Liu B, Ruan B Y. 1994. The finite element method for solving anomalous potential for resistivity surveys[J]. Chinese J. Geophys. (in Chinese), 37(S2): 511-515. |
| [23] | Xu X H. 2009. Application of well-ground potential image in Daqing oil field (in Chinese)[Master thesis]. Beijing: China University of Geosciences. |
| [24] | Zhang Y. 2009. The forward modeling of three-dimensional borehole-to-surface logging technology (in Chinese)[Master thesis]. Qingdao: Ocean University of China. |
| [25] | Zhu K G, Jia Z S, Wang Y Z, et al. 2013. Research on borehole-surface joint electrical double-parameter monitoring for the hydraulic fracturing in oilfields[J]. Chinese J. Geophys. (in Chinese), 56(11): 3663-3672, doi: 10.6038/cjg20131107. |
| [26] | Zhu T, Feng R, Xu S X, et al. 2008. Electrical imaging theory and application for vertical line power[J]. Oil Geophysical Prospecting (in Chinese), 43(4): 462-466. |
| [27] | 蔡圣权, 叶义平, 邹鲁新,等. 2005. 井—地电位成像技术在新疆油田五1区剩余油分布评价研究中的应用[J]. 特种油气藏, 12(5): 55-58, 65. |
| [28] | 戴前伟, 陈德鹏, 熊健奎,等. 2008. 垂直线源井-地电位探测地下动态导体的三维有限元数值模拟[J]. 工程地球物理学报, 5(6): 643-647. |
| [29] | 戴前伟, 陈德鹏, 刘海飞,等. 2012. 复杂管网线源井地电位三维有限元模拟[J]. 石油地球物理勘探, 47(6): 998-1005. |
| [30] | 柯敢攀, 黄清华. 2009. 井地电法的三维正反演研究[J]. 北京大学学报(自然科学版), 45(2): 264-272. |
| [31] | 李艾红, 苏运动, 王汉林,等. 2008. 井地电位成像技术在双河油田的应用[J]. 石油地质与工程, 22(5): 78-80. |
| [32] | 李长伟, 阮百尧, 吕玉增,等. 2010. 点源场井-地电位测量三维有限元模拟[J]. 地球物理学报, 53(3): 729-736, doi: 10.3969/j.issn.0001-5733.2010.03.028. |
| [33] | 李心刚. 1986. 垂直线源电阻率法研究[J]. 石油地球物理勘探, 21(2): 197-207. |
| [34] | 凌明友, 郝新武, 程同军,等. 2003. 井—地电位成像技术研究剩余油分布[J]. 断块油气田, 10(4): 55-58. |
| [35] | 刘地渊, 徐凯军, 赵广茂,等. 2006. 任意形状线电流源三维地电场研究[J]. 地球物理学进展, 21(2): 395-399, doi: 10.3969/j.issn.1004-2903.2006.02.010. |
| [36] | 刘海飞, 陈德鹏, 戴前伟,等. 2011. 连续电性介质线源井-地电位三维有限元数值模拟[J]. 桂林理工大学学报, 31(1): 28-38. |
| [37] | 马捷, 冯德山, 刘海飞,等. 2010. 井地电位法中变物性参数异常响应的模拟与分析[J]. 物探化探计算技术, 32(1): 1-5. |
| [38] | 屈有恒. 2008. 井地电阻率法及双频激电三维数值模拟与反演研究[博士论文]. 北京: 中国地质大学(北京). |
| [39] | 谭河清, 沈金松, 周超,等. 2004. 井-地电位成像技术及其在孤东八区剩余油分布研究中的应用[J]. 石油大学学报(自然科学版), 28(2): 31-37. |
| [40] | 幸娟. 2010. 三维井—地多参数电法数值模拟及对比研究[硕士论文]. 长春: 吉林大学. |
| [41] | 徐凯军, 李桐林. 2006. 垂直有限线源三维地电场有限差分正演研究[J]. 吉林大学学报(地球科学版), 36(1): 137-141. |
| [42] | 徐世浙, 刘斌, 阮百尧. 1994. 电阻率法中求解异常电位的有限单元法[J]. 地球物理学报, 37(增刊I): 511-515. |
| [43] | 徐晓会. 2009. 井地电位成像技术在大庆油田的应用 [硕士论文]. 北京: 中国地质大学(北京). |
| [44] | 章钰. 2009. 三维井—地电位测井技术的正演模拟研究[硕士论文]. 青岛: 中国海洋大学. |
| [45] | 朱凯光, 贾正森, 王言章,等. 2013. 油田压裂井地电法双参数联合监测技术与仪器研究[J]. 地球物理学报, 56(11): 3663-3672, doi: 10.6038/cjg20131107. |
| [46] | 朱涛, 冯锐, 徐苏欣,等. 2008. 垂直线源电成像理论及应用[J]. 石油地球物理勘探, 43(4): 462-466. |
 2015, Vol. 30
2015, Vol. 30


