地球物理学进展  2015, Vol. 30 Issue (4): 1818-1824   PDF    
引用本文
严君, 刘洪. 2015. 基于复正则化非稳态回归Wigner-ville分布谱分解及其应用. 地球物理学进展, 30(4): 1818-1824, doi: 10.6038/pg20150440  
YAN Jun, LIU Hong. 2015. Wigner-Ville distribution-based spectral decomposition using complex regularized nonstationary regression and its application. Progress in Geophysics, 30(4): 1818-1824, doi: 10.6038/pg20150440   
基于复正则化非稳态回归Wigner-ville分布谱分解及其应用
严君1,2, 刘洪1     
1. 中国科学院地质与地球物理研究所中国科学院油气资源研究重点实验室, 北京 100029;
2. 中国科学院大学, 北京 100049
收稿日期: 2015-03-18 修回日期: 2015-05-18.
基金项目: 国家油气重大专项(2011ZX05023-005-002)和国家高技术研究发展计划(863)(2012AA061202)联合资助.
作者简介: 严君,男,1987年生,中国科学院地质与地球物理研究所在读硕士研究生,主要从地震波传播与成像、多次波衰减和时频分析等研究.(E-mail:junyan@mail.iggcas.ac.cn)
通讯作者: 刘洪,男,1959年生,研究员,主要从事油储地球物理研究.(E-mail:liuhong@mail.igcas.ac.cn)
摘要: 谱分解是应用于油气藏描述的一种有效方法.谱分解方法如短时傅里叶变换、连续小波变换、S变换等因使用预先选定的窗函数和基函数限制了其时频分辨率.对于双线性Wigner-Ville分布(WVD)谱分解,其在计算时频分布不要求选定窗函数,时间和频率分辨率均很高,但存在交叉噪声.在本文中,我们提出利用迭代反演方法计算WVD谱分解.其关键思想是,利用复正则化非稳态回归技术拟合解析地震道和它的傅里叶分量,并且将时变的傅里叶系数定义为WVD时频分布.理论合成数据表明,基于复正则化非稳态回归WVD谱分解方法有较高的时间频率分辨率,并且能有效地压制交叉噪声.最后,我们将本文方法应用于三维实际地震数据进行河道检测.
关键词: Wigner-Ville分布     谱分解     复正则化非稳态回归     交叉噪声    
Wigner-Ville distribution-based spectral decomposition using complex regularized nonstationary regression and its application
YAN Jun1,2, LIU Hong1     
1. Key Laboratory of Petroleum Resources Research, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
2. University of Chinese Academy of Sciences, Beijing 100049, China
Abstract: Spectral decomposition is an effective method for reservoir characterization in seismic data processing and interpretation. The widely used spectral methods such as short-time Fourier transform (STFT), continuous-wavelet transform (CWT) and S transform have limited time-frequency resolution owing to the use of the pre-defined window and base functions. In bilinear spectral decompositions, Wigner-Ville Distribution (WVD) achieves a high resolution in both the time and frequency domains because of no window used in calculating the time frequency representations. However, the WVD suffers from the cross-term interference due to its quadratic nature. In this paper, we propose a new method to implement WVD-based spectral decomposition in the framework of iterative inversion. The key idea is based on fitting the analytic seismic traces to all its Fourier components using complex regularized nonstationary regression. The time-varying Fourier coefficients are defined as the WVD to represent the time-frequency map. Synthetic examples demonstrate that the proposed method can obtain a high time-frequency resolution and at the same time effectively reduce the cross-term interference. Finally, we apply the proposed method to the 3D field data for channel detection.
Key words: Wigner-Ville Distribution     spectral decomposition     complex regularized nonstationary regression     cross-term interference    
0 引 言

谱分解或时频分析能对油气藏提供十分重要信息(Partyka et al.，1999; Marfurt and Kirlin，2001; Castagna et al.，2003; 陈学华等，2009; Li et al.，2011).在过去的20年里，用于时频分析的谱分解方法得到了充分的发展.应用最为广泛的谱分解方法如短时傅里叶变换(STFT)(Allen，1977)、连续小波变换(CWT)(Chakraborty and Okaya，1995，高静怀等，1997；王西文等，2002)，S变换(Stockwell et al.，1996；高静怀等，2003；刘喜武等，2006; 张固澜，2011; 景建恩等，2012)，匹配追踪分解(MPD)(Mallat and Zhang，1993; Wang，2007，2010; 张繁昌和李传辉，2012；武国宁等，2012)等.上述这些方法均是线性时频变换方法，其通过计算信号和一系列时频函数的互相关来描述的(Li and Zheng，2008)，并且时间和频率分辨率受窗函数和基函数限制(Cohen，1995).与此相反，双线性时频分布—著名的Cohen类(Cohen，1995)，如WVD分布基于时频能量密度，时频分辨率高且有很多好的数学性质.所有的时频描述均能从Cohen类推导而来，可理解为加权平均的WVD(Mallat，1996).Matt(2007)认为谱分解可作为信号模糊函数与核函数之积.例如，WVD的核函数为常数1，这意味着计算WVD不需要窗函数.对于短时傅里叶变换(STFT)谱，其核为加窗的模糊函数；对于连续小波变换(CWT)，其核为一系列小波母函数组成的模糊函数.这些经调整的模糊函数在一定程度上使时频分布更为光滑.与WVD相比，STFT和CWT时间频率分辨率均会减小.然而，WVD因交叉噪声的影响，其应用受到限制.减少交叉噪声最常见的方法是引入合适的核函数(Cohen，1995).以独立的时间和频率窗函数作为核的光滑伪WVD(SPWVD)(Hlawatsch et al.，1995)能达到相对较高的时间频率分辨率同时能减少交叉噪声.

正则化非稳态回归(RNR)起初由Fomel提出并应用于多次波自适应相减(Fomel，2009).非稳态回归借助于整形正则化技术(Fomel，2007)拟合数据和基函数得到非稳态系数.Liu等(2011)利用RNR计算地震道随时间变化的傅里叶系数作为时频图.基于同样思想，Liu和Fome(2013)将RNR拓展应用到局部时频分解、局部时间—频率—波数和局部空间—频率—波数分解.Fomel(2013)进一步将RNR和正则化非稳态自回归(RNAR)(Liu and Fomel，2011; Liu et al.，2012)应用到自回归谱分解.

本文提出利用复正则化非稳态回归(CRNR)计算WVD谱分解.其主要思想是，通过CRNR拟合解析地震道和它们对应的傅里叶分量求出时变的傅里叶系数，并且将时变的傅里叶系数定义为WVD时频分布.通过几个标准测试例子，我们对比了本文方法和线性时频变换(如STFT，S变换)以及双线性时频变换(WVD，SPWVD)测试结果，并表明了此方法有较高的时间频率分辨率同时能有效地消除交叉噪声.最后，我们将本文方法应用于3D实际地震数据河道检测.

1 方法原理1.1 Wigner-Ville 分布

Wigner-ville分布定义为(Boashash and Black，1987)

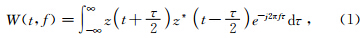
其中z(t)为实信号，x(t)对应的解析信号，t为时间，τ为延时，f为频率，*为复转置.在时间域，解析信号z(t)定义为

其中，H为实信号x(t)的Hilbert变换.注意到函数z(t)在乘积中出现两次，这样使其分布为双线性.实际上，WVD可通过如下方式构造，首先计算解析信号的互相关，然后将其变换到傅里叶域.由于双线性性质，上述方法计算的WVD会产生交叉噪声.尽管交叉噪声可以通过选择恰当的光滑算子得到压制，但同时WVD的时间频率分辨率会降低.接下来，我们将介绍利用迭代反演方法计算WVD谱分解.

1.2 利用复正则化非稳态回归计算WVD谱分解

z(n)表示离散的解析信号，n=0，…，N－1，其中N为采样总个数.离散WVD可表示为

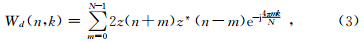
其中互相关函数定义为

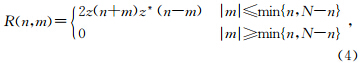
注意到WVD的频率变量的周期为傅里叶变换的一半，但利用解析信号可以避免两倍Nyquist采样率限制.等价于WVD的逆变换形式如下

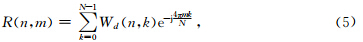
类似于基于RNR局部时频分解，本文中我们利用CRNR求解WVD谱分解.上述方程可以利用最小二乘最优化求解

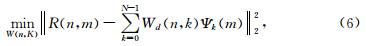
其中Ψ(m)表示傅里叶基函数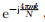，注意到R(n，m)和Wd(n，k)分别为复数和实数.正则化非稳态回归可以允许被估计的Wd(n，k)随n变换.上述最优化问题在数学上是病态问题，因求解的未知变量比约束方程更多.为了解决病态问题，我们需要引进正则化约束使被估计的Wd(n，k)具有一些比较好的数学性质，如光滑性.若引入经典的Tikhonov正则化技术，方程可写为

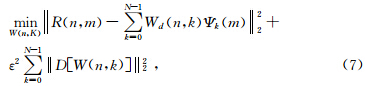
其中D为Tikhonov正则化算子(如粗糙算子)，ε为尺度因子.

在本文中，我们采用整形正则化而非Tikhonov正则化约束最小二乘反演.整形正则化(Fomel，2007)在迭代最优化中通过显式地将被估计的模型映射到所需要的模型施加约束.它能很方便地对所需估计的模型施加约束并且能是优化问题有更快的收敛速度.为了方便地从Tikhonov正则化算子引入整形正则化，我们将公式(5)可以写成线性方程 Ax=b形式，其中A为正演算子，x为模型，b为数据.Tikhonov正则化约束最小二乘反演目标函数为

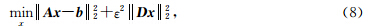
其中，D为Tikhonov正则化算子，ε为尺度因子.公式(8)的解可写为

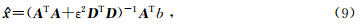
其中，AT为伴随算子.Fomel(2007)将整形算子S定义为：

将公式(10)带入公式(9)可得到整形正则化最小二乘解

若引入尺度因子λ，公式(11)可写为

上式中x可采用共轭梯度方法迭代求解，其收敛速度比采用经典的Tikhonov正则化约束方法(公式8)快.特别地，我们选择高斯窗函数(其大小可调整)作为整形算子.

尽管WVD表达式在数学上为实函数，利用CRNR迭代计算的Wd(n，k)却为复数.因此，我们将随时间变化的Wd(n，k)的绝对值(模)定义为WVD时频分布.值得注意的是，整形算子的长度可控制谱分解的收敛速度和时频分辨率.

2 模型试算

为了测试本文方法的有效性，我们首先利用标准合成数据比较了本文方法，STFT，S变换，WVD以及SPWVD.然后，我们将本文方法应用于三维实际地震数据进行河道检测.

第一个合成数据来源于Liu和Fomel(2003)和Lu和Li(2013)，其由两个交叉的非稳态的鸟鸣信号组成，如图 1所示.图 2为WVD和SPWVD谱分解结果，其中SPWVD时间和频率窗函数大小取不同值.在图 2b、2c和2d中，SPWVD谱分解时间和频率窗函数大小(采样点数)分别为TW=25、FW=25，TW= 25、FW=35，TW=45、FW=45.通过比较图 2a~d，我们发现WVD时间频率分辨率最高，但存在交叉噪声，而SPWVD压制了交叉噪声，时间频率分辨率下降(陈雨红等，2006).此外，SPWVD的时间频率分辨率很大程度上依赖于时间和频率窗函数大小.图 3为STFT、S变换和本文方法得到的谱分解结果.由于STFT通过滑动时窗来计算频谱，其时间和频率分辨率受Heisenberg测不准原理限制.当滑动时窗较小时，STFT有较高的时间分辨率，但是频率分辨能力较差.当滑动时窗较大时，STFT有较高的频率分辨率，但频率分辨能力却较差.而S变换是一种介于STFT和CWT的时频分析方法，它结合了STFT和CWT各自的优点.对比图 3a和图 3b不难发现S变换的结果比STFT结果稍好，但S变换对于低频率虽然有较高的分辨率但其对较高频率成分分辨率较低.图 3c和图 3d为本文方法谱分解结果，从图中可发现线性频率分布趋势有较高的分辨率同时不存在交叉噪声.图 3c和图 3d所使用的整形正则化光滑半径(采样点数)分别为SR=7和SR=15，反演迭代次数分别为15次和55次.注意到，使用不同整形正则化光滑半径得到的谱分解结果几乎一致，而SPWVD方法的结果很大程度受到时间和频率窗函数大小的影响，如图 2所示.

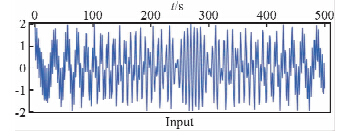图 1 两个交叉的非稳态的鸟鸣信号Fig. 1 Input synthetic data with two crossing nonstationary chirp signals

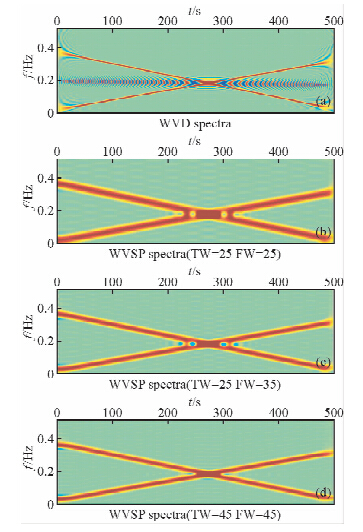图 2 谱分解结果(a)WVD(b)SPWVD，其中时间和频率窗函数大小为25，25(c)SPWVD，其中时间和频率窗函数大小为25，35(d)SPWVD，其中时间和频率窗函数大小为45，45.SPWVD结果很大程度依赖于窗函数大小Fig. 2 The spectral decomposition results obtained with(a)WVD(b)SPWVD(the time and frequency windows are 25 and 25)(c)SPWVD(the time and frequency windows are 25 and 35(d)SPWVD(the time and frequency windows are 45 and 45). Note that the results of SPWVD are heavily depended on the size of windows

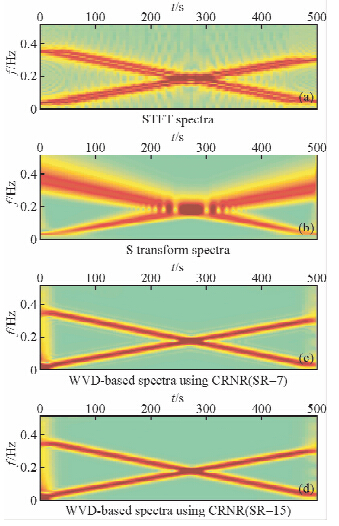图 3 谱分解结果(a)STFT(b)S变换(c)本文方法，其中整形正则化半径为7(d)本文方法，其中整形正则化半径为15.不同整形正则化光滑半径得到的谱分解结果几乎一致Fig. 3 The spectral decomposition results obtained with(a)STFT(b)S transform(c)the proposed method where smoothing radius is 7(d)the proposed method where smoothing radius is 15. Note that different size of smoothing radius results in nearly the same results in the proposed method

第二个标准测试模型来源于Liu等(2011)和Fomel(2013)，其包含两个非稳态的频率呈抛物线变换的鸟鸣信号，如图 4所示.图 5为WVD和SPWVD谱分解结果，其中SPWVD时间和频率窗函数大小取不同值.在图 5b、5c和5d中，SPWVD谱分解时间和频率窗函数大小(采样点数)分别为TW=25、FW=25，TW=25、FW=35，TW=55、FW=45.图 6为STFT、S变换和本文方法得到的谱分解结果.结果如第一个测试例子一样，本文方法得到的谱分解结果显示线性频率分布趋势有较高的分辨率同时不存在交叉噪声.WVD、STFT和S变换方法有各自的缺点如WVD存在交叉噪声，STFT和S变换在低频率成分有较高的分辨率，在高频率成分分辨率下降.从图 5、图 6c和图 6d可看出，尽管SPWVD方法得到的谱分解分辨率比本文方法高，但SPWVD需要选择恰当的时间和频率窗函数.

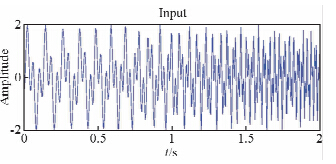图 4 两个非稳态的频率呈抛物线变换的鸟鸣信号Fig. 4 Input synthetic data with two smoothly parabolic frequencies chirp signals

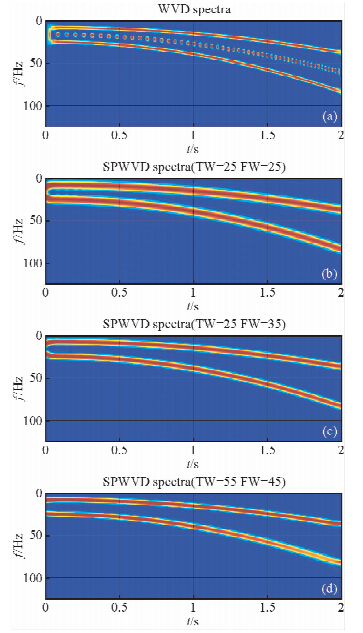图 5 谱分解结果(a)WVD(b)SPWVD，其中时间和频率窗函数大小为25，25(c)SPWVD，其中时间和频率窗函数大小为25，35(d)SPWVD，其中时间和频率窗函数大小为55，45Fig. 5 The spectral decomposition results obtained with(a)WVD(b)SPWVD(the time and frequency windows are 25 and 25)(c)SPWVD(the time and frequency windows are 25 and 35(d)SPWVD(the time and frequency windows are 55 and 45

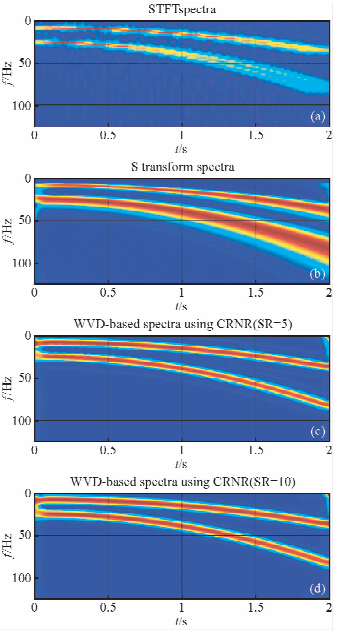图 6 谱分解结果(a)STFT(b)S变换(c)本文方法，其中整形正则化半径为5(d)本文方法，其中整形正则化半径为10.对比图 5，尽管SPWVD方法得到的谱分解分辨率比本文方法高，但SPWVD需要选择恰当的时间和频率窗函数Fig. 6 The spectral decomposition results obtained with(a)STFT(b)S transform(c)the proposed method where smoothing radius is 5(d)the proposed method where smoothing radius is 10. Note that the results of SPWVD is somewhat better than our method，but SPWVD has to select appropriate time and frequency windows as shown in Figure 5
3 实际资料应用

检测河道系统是油藏描述重要一部分.详尽的河道系统描述可为分析沉积环境提供有力帮助(Liu and Marfurt，2007).谱分解常用于凸显河道系统(Partyka et al.，1999).我们将本文方法应用到墨西哥3D实际地震资料(图 7a所示)用于检测河道系统.图 7b为三维数据体的水平切片.图 8为不同频率成分的时频切片，相比较与水平切片，我们可发现较高频谱分解，如30 Hz、40 Hz、50 Hz切片，河道地质形态有清晰呈现，如红色箭头所示.

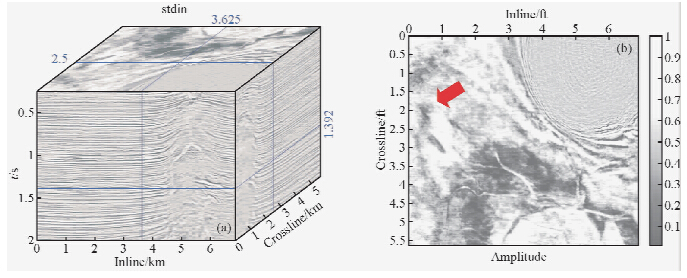图 7(a)3D墨西哥Gulf地震数据体(b)水平时间切片.蓝线表明纵测线、联络测线、水平切片位置Fig. 7(a)3D seismic image from Gulf of Mexico and (b)the time slice. Blue lines identify the location of inline，crossline sections and time slice

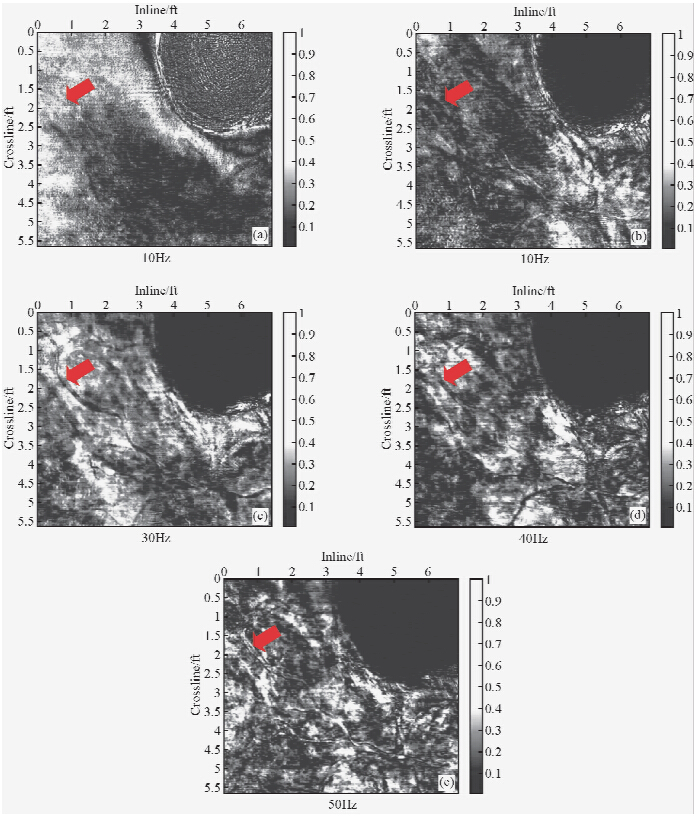图 8 谱分解切片(a)10 Hz(b)20 Hz(c)30 Hz(d)40 Hz(e)50 Hz.通过比较，我们可发现不同频率切片对河道有着不同程度刻画Fig. 8 Spectral decomposition slices with(a)10 Hz(b)20Hz(c)30 Hz(d)40 Hz(e)50 Hz. With careful comparison，we can see different time frequency slice displays some clearly visible channels
4 结 论

在本文中，我们提出利用复正则化非稳态回归计算WVD谱分解，其主要思想是，通过CRNR拟合解析地震道和它们所对应的傅里叶分量求出时变的傅里叶系数，并且将时变的傅里叶系数定义为WVD时频分布.数值试验结果表明，本文方法能有效地对非平稳信号进行谱分解，而且其时间分辨率和频率分辨率比线性时频变换如STFT、S变换更高.此外，本文方法可以有效消除双线性WVD存在的交叉噪声；相比与SPWVD方法，本文方法采用迭代反演求取时频分布，不需要设定时间窗函数和频率窗函数，且整形正则化光滑半径大小比SPWVD方法中窗函数大小对谱分解结果影响更小.最后，三维墨西哥Gulf地震数据体测试结果表明，本文谱分解方法可有效地应用于河道检测.将本文方法应用于地震属性分析、地震相描述、薄层识别等方面，有待进一步研究.

致 谢    感谢Madagascar(http://www.ahay.org)开发社区对本文的帮助.

参考文献
[1] Allen J B. 1977. Short term spectral analysis, synthesis, and modification by discrete Fourier transform[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 25(3): 235-238.
[2] Boashash B, Black P J. 1987. An efficient real-time implementation of the Wigner-ville distribution[J]. IEEE Transactions on Acoustics, Speech Signal Processing, 35(11): 1611-1618.
[3] Castagna J P, Sun S, Siegfried R. 2003. Instantaneous spectral analysis: Detection of low-frequency shadows associated with hydrocarbons[J]. The Leading Edge, 22(2): 120-127.
[4] Chakraborty A, Okaya D. 1995. Frequency-time decomposition of seismic data using wavelet-based methods[J]. Geophysics, 60(6): 1906-1916.
[5] Chen X H, He Z H, Huang D J, et al. 2009. Low frequency shadow detection of gas reservoirs in time-frequency domain[J]. Chinese J. Geophys. (in Chinese), 52(1): 215-221.
[6] Chen Y H, Yang C C, Cao Q F, et al. 2006. The comparison of some time-frequency analysis methods[J]. Progress in Geophysics (in Chinese), 21(4): 1180-1185.
[7] Fomel S. 2007. Shaping regularization in geophysical-estimation problems[J]. Geophysics, 72(2): R29-R36.
[8] Fomel S. 2009. Adaptive multiple subtraction using regularized nonstationary regression[J]. Geophysics, 74(1): V25-V33.
[9] Fomel S. 2013. Seismic data decomposition into spectral components using regularized nonstationary autoregression[J]. Geophysics, 78(6): O69-O76.
[10] Gao J H, Chen W C, Li Y M, et al. 2003. Generalized S transform and seismic response analysis of thin interbeds[J]. Chinese J. Geophys. (in Chinese), 46(4): 526-532.
[11] Gao J H, Wang W B, Zhu G M. 1997. Wavelet transform and instantaneous attributes analysis[J]. Acta Geophysica Sinica (in Chinese), 40(6): 821-832.
[12] Hlawatsch F, Manickam T G, Urbanke R L, et al. 1995. Smoothed pseudo-Wigner distribution, Choi-Williams distribution, and cone-kernel representation: Ambiguity-domain analysis and experimental comparison[J]. Signal Processing, 43(2): 149-168.
[13] Jing J E, Wei W B, Chen H Y, et al. 2012. Magnetotelluric sounding data processing based on generalized S transformation[J]. Chinese J. Geophys. (in Chinese), 55(12): 4015-4022.
[14] Li Y D, Zheng X D. 2008. Spectral decomposition using Wigner-Ville distribution with applications to carbonate reservoir characterization[J]. The Leading Edge, 27(8): 1050-1057.
[15] Li Y D, Zheng X D, Zhang Y. 2011. High-frequency anomalies in carbonate reservoir characterization using spectral decomposition[J]. Geophysics, 76(3): V47-V57.
[16] Liu G C, Fomel S, Chen X H. 2011. Time-frequency analysis of seismic data using local attributes[J]. Geophysics, 76(6): P23-P34.
[17] Liu G C, Chen X H, Du J, et al. 2012. Random noise attenuation using f-x regularized nonstationary autoregression[J]. Geophysics, 77(2): V61-V69.
[18] Liu J L, Marfurt K J. 2007. Instantaneous spectral attributes to detect channels[J]. Geophysics, 72(2): P23-P31.
[19] Liu X W, Liu H, Li Y M, et al. 2006. Study on characteristics of seismic stratigraphy by generalized S-transform[J]. Progress in Geophysics (in Chinese), 21(2): 440-451.
[20] Liu Y, Fomel S. 2011. Seismic data interpolation beyond aliasing using regularized nonstationary autoregression[J]. Geophysics, 76(5): V69-V77.
[21] Liu Y, Fomel S. 2013. Seismic data analysis using local time-frequency decomposition[J]. Geophysical Prospecting, 61(3): 516-525.
[22] Lu W K, Li F Y. 2013. Seismic spectral decomposition using deconvolutive short-time Fourier transform spectrogram[J]. Geophysics, 78(2): V43-V51.
[23] Mallat S. 1996. A Wavelet Tour of Signal Processing[M]. 2nd ed. London: Academic Press.
[24] Mallat S G, Zhang Z. 1993. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 41(12): 3397-3415.
[25] Marfurt K J, Kirlin R L. 2001. Narrow-band spectral analysis and thin-bed tuning[J]. Geophysics, 66(4): 1274-1283.
[26] Partyka G, Gridley J, Lopez J. 1999. Interpretational applications of spectral decomposition in reservoir characterization[J]. The Leading Edge, 18(3): 353-360.
[27] Stockwell R G., Mansinha L, Lowe R P. 1996. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing, 44(4): 998-1001.
[28] Wang X W, Yang K Q, Zhou L H, et al. 2002. Methods of calculating coherence cube on the basis of wavelet transform[J]. Chinese J. Geophys. (in Chinese), 45(6): 847-853.
[29] Wang Y H. 2007. Seismic time-frequency spectral decomposition by matching pursuit[J]. Geophysics, 72(1): V13-V20.
[30] Wang Y H. 2010. Multichannel matching pursuit for seismic trace decomposition[J]. Geophysics, 75(4): V61-V66.
[31] Wu G L, Cao S Y, Sun N. 2012. Matching pursuit method based on complex seismic traces and its application of hydrocarbon exploration[J]. Chinese J. Geophys. (in Chinese), 55(6): 2027-2034, doi: 10.6038/j.issn.0001-5733.2012.06.024.
[32] Zhang F C, Li C H. 2012. Orthogonal time-frequency atom based fast matching pursuit for seismic signal[J]. Chinese J. Geophys. (in Chinese), 55(1): 277-283, doi: 10.6038/j.issn.0001-5733.2012.01.027.
[33] Zhang G L. 2011. Low-frequency absorption attenuation gradient detection based on improved generalized S transform[J]. Chinese J. Geophys. (in Chinese), 54(9): 2407-2411, doi: 10.3969/j.issn.0001-5733.2011.09.024.
[34] 陈学华, 贺振华, 黄德济,等. 2009. 时频域油气储层低频阴影检测[J]. 地球物理学报, 52(1): 215-221.
[35] 陈雨红, 杨长春, 曹齐放,等. 2006. 几种时频分析方法比较[J]. 地球物理学进展, 21(4): 1180-1185.
[36] 高静怀, 陈文超, 李幼铭,等. 2003. 广义S变换与薄互层地震响应分析[J]. 地球物理学报, 46(4): 526-532.
[37] 高静怀, 汪文秉, 朱光明. 1997. 小波变换与信号瞬时特征分析[J]. 地球物理学报, 40(6): 821-832.
[38] 景建恩, 魏文博, 陈海燕,等. 2012. 基于广义S变换的大地电磁测深数据处理[J]. 地球物理学报, 55(12): 4015-4022.
[39] 刘喜武, 刘洪, 李幼铭,等. 2006. 基于广义S变换研究地震地层特征[J]. 地球物理学进展, 21(2): 440-451.
[40] 王西文, 杨孔庆, 周立宏,等. 2002. 基于小波变换的地震相干体算法研究[J]. 地球物理学报, 45(6): 847-853.
[41] 武国宁, 曹思远, 孙娜. 2012. 基于复数道地震记录的匹配追踪算法及其在储层预测中的应用[J]. 地球物理学报, 55(6): 2027-2034, doi: 10.6038/j.issn.0001-5733.2012.06.024.
[42] 张繁昌, 李传辉. 2012. 基于正交时频原子的地震信号快速匹配追踪[J]. 地球物理学报, 55(1): 277-283, doi: 10.6038/j.issn.0001-5733.2012.01.027.
[43] 张固澜. 2011. 基于改进的广义S变换的低频吸收衰减梯度检测[J]. 地球物理学报, 45(6): 2407-2411, doi: 10.3969/j.issn.0001-5733.2011.09.024.