叠前偏移得到的共反射点(CRP)道集由反映地下同一点的反射信息组成,理论上基本消除了界面弯曲和倾斜地层的影响(程玉坤等,2008),对一系列共反射点道集的全叠加即得到偏移剖面.对于精确构造成像,由于受地震资料信噪比、道集不平、子波动校拉伸等因素的影响,共反射点道集的叠加并不能得到理想的成像结果.对于基于CRP道集的叠前反演,对道集的处理提出了更高的要求,除了要提高地震数据的信噪比和压制噪声的同时必须保持反射波振幅的相对强弱关系(张征等,2012),如何获得高信噪比且同相轴水平的叠前资料直接影响着反演结果的稳定性和准确性.因此,无论是对于构造成像还是叠前反演,对共反射点道集进行一定的优化处理,显得十分必要.
低信噪比资料得到的共反射点道集存在的问题主要表现在三个方面.
(1)信噪比问题.得到共反射点道集的过程一般是在叠前实现的,噪声的存在使得其信噪比一般比较低(刘振等,2013),传统处理中的噪声以随机噪声居多,可以采用叠前去除随机噪声方法来消除或压制,如f-k域倾向滤波、f-x域预测滤波、中值滤波等,但是这些滤波方法没有方向特性,易造成对倾斜同相轴振幅的压制,同时也会模糊小的断层和裂缝等不连续结构(王伟等,2012).结构滤波是一种具有地层倾向的滤波方法,能够用于叠前资料的噪声压制,并且具有保护边缘结构的良好特性,如何有效地对地层倾向进行估计是该方法的关键.目前,地层倾向的估计主要有复数道分析、离散扫描、梯度结构张量三种方法(Eichkitz et al.,2012),Luo等(1996)基于复数道分析来对地层倾向进行估计,该方法是通过分析道属性计算出瞬时频率和瞬时波数并求两者的比值来估计不同测线上的视倾角,此方法估计倾向时往往会产生一定的干扰,为了克服这个问题Barnes(2000)对此方法进行了改进;Marfurt等(1998)基于地震数据离散扫描来估计地层倾向,该方法是在中心点位置所在时窗内取不同的倾角进行相关扫描,当相关值最大时即为当前瞬时倾向,改进后目标函数的扫描可以进一步提高扫描精度(Gersztenkorn and Marfurt,1999; Bednar,1998),该方法的特点是实现容易、计算效率高;Bakker(2002)和Hocker(2002)基于梯度结构张量来估计地层方向,该方法是在分析时窗内计算地震数据梯度,与梯度值变化最大方向正交的方向即为地层方向,但该方法会产生新的干扰.
(2)道集拉平问题.共反射点道集中反射波同相轴理论上应是水平同相轴,但由于受地层各向异性、资料信噪比、速度等因素的影响,叠前偏移后的共反射点道集中往往存在剩余时差,表现为同一点的反射信息在道集中聚焦不好,同相轴不能很好对齐.目前,道集拉平主要有静校正法和速度法(Singleton,2009)两类方法,其中静校正法是假定在地震射线路径上局部速度扰动引起道集同相轴波动,可看作静校正量误差引起,而速度法是假定道集不平是由剩余动校引起.静校正法一般基于互相关原则,通过计算滑动时窗内待校正地震道和模型地震道间的互相关值,以最优化原则逐道估计剩余校正量剩余校正量(Hinkley et al.,2004;Gulunay et al.,2007).速度法则可以通过二阶和四阶均方根速度场高分辨率估计来进行矫正(Swan,2001),张征等(2012)利用各向异性速度分析来消除剩余时差时,针对各向异性参数求取困难且效率低下这一问题,提出应用高密度双谱扫描的方法,得到两个与各向异性参数有关的量值,最终将其转化为各向异性参数来消除叠前道集中的剩余时差;此外,孙建国(2001)、王开燕等(2007)以相位替换为基础,通过计算模型道的相位谱,然后对待校正道的相位谱进行替换来计算剩余校正量.
(3)动校拉伸造成频率损失问题.由于远道在道集拉平过程中子波拉伸会造成高频衰减,表现为大偏移距处道集频率降低,波形“发胖”而产生畸变现象.很多学者对于动校拉伸对叠加和AVO分析的影响进行了深入的研究,其中Dunkin和Levin(1973)是最早研究动校拉伸现象的学者之一,并推导了由动校正、速度和偏移距引起的子波拉伸校正解析关系式;Castoro等(2001)对于动校拉伸现象进行了详细的解析,并提出了具有实际可行的校正措施;Lazaratos和Finn(2004)利用频谱整形滤波的方法对子波拉伸进行了校正;Roy(2005)在层状介质偏移中利用反射角对子波拉伸进行校正;Pérez和Marfurt(2006)在共反射角偏移后对子波进行校正.
针对共反射点道集中存在的信噪比和道集拉平问题,本文提出利用二次多项式对地震数据进行拟合来估计地层倾向并结合结构中值滤波来提高CRP道集信噪比以及对道集进行剩余时差校正的优化处理.
1 方法原理1.1 地层倾向估计地层倾向估计的方法很多(Eichkitz et al.,2012),离散扫描法是其中一种简单且计算效率高的方法,该方法基于同相轴在局部满足线性的假设,对离散点在计算时窗内求相关.
为了使得倾向的估计更加准确,本文采用常规二次多项式对地震数据进行拟合来估计地层倾向(夏洪瑞等,2006),此方法是对正交多项式拟合方法(俞寿朋,1993)的改进,克服了正交多项式拟合方法的不足,其方法原理如下.
假设在计算滑动时窗内,局部同相轴满足二次拟合多项式.
t=t0+c1x+c2x2,
其中:x为拟合中心道的相对道号,x有正负方向,其取值为x=-M,-M+1,…,-1,0,1…,M-1,M,M为拟合道数的一半,t0为拟合中心点的时间.为了减少计算量,可以先对一次项系数进行扫描,然后进行二次项系数扫描.一次项最佳拟合系数的确定采用最大互相关法则,在给定系数初始范围内,对不同系数求拟合道互相关,当互相关值最大时的系数即为最佳拟合系数,互相关目标函数.
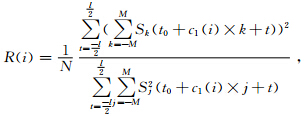
其中:R(i)为时窗内道集互相关值,Sk,Sj为拟合道样点值,l为相关时窗内样点数.相关系数R(i)在0~1间变化,理想情况下,当时窗内为同相轴方向时各道相关性最强,此时R(i)趋于1,R(i)越小则相关性越差.计算一次项系数时,对于道集中的每一个样点,在计算时窗内通过给定不同的系数(倾向方向)计算其相关值,当相关值R(i)最大时的系数即为当前样点的最佳一次项拟合系数,同理再对二次项系数进行扫描,最终得到当前样点的最佳二次拟合多项式,此时拟合方向即为当前样点所在同相轴方向.如图 1所示,拟合道集的中心道为参考道,蓝线为一次项拟合系数扫描范围,当扫描方向为计算样点所在同相轴方向时(红线所示)相关值为最优值,一次项系数确定后,再对二次项系数进行扫描来进一步提高拟合精度.
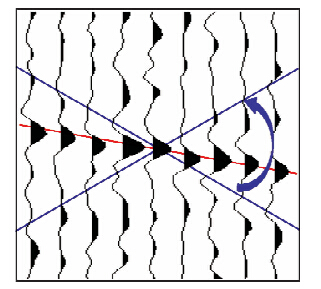 | 图 1 离散扫描法估计地层倾向示意图Fig. 1 Schematic for the estimation of dip using the discrete scanmethod |
Eichkitz等(2012)和Liu(2013)针对共反射点道集在AVO分析中需要满足的应用条件,提出利用结构滤波(Structural Filter)来压制随机噪声,此方法原理上和Luo等(2002)提出的保边滤波(EPS)算法类似,与常规中值滤波方法的不同之处在于其滤波具有方向性.基于常规二次多项式对同相轴追踪后,在滑动时窗内以中心样点同相轴所在方向运用中值滤波,滤波结果作为最终中心样点的输出.由最小距离理论知,中值可定义为序列中与其他所有点距离和最小的序列点,则中值am表达式为(Liu,2013).
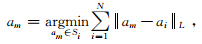
其中N为序列个数,L为范数. 滑动时窗依次沿着时间T轴和X轴方向滑动即完成一个共反射点道集的处理,本文讨论的结构中值滤波相对于常规随机噪声压制方法具有以下优点:(1)在一定倾向方向上进行滤波处理;(2)无论同相轴是否水平,都能对随机噪声和异常振幅进行有效压制;(3)滤波的同时保护断层边界,能够保护断层的不连续性.因此,结构中值滤波不仅能够有效地衰减随机噪声、提高剖面的信噪比,而且能够较好地保持有效信号和断层、裂缝等地层边缘和细节特征(王伟等,2012).
1.3 道集拉平静校正法道集拉平中,借助道集叠加(全叠加或近-中道部分叠加)来建立标准模型道,然后以模型道作为标准对处理道集进行剩余时差校正,因此标准模型道的求取是校正效果好坏的关键.借助道集叠加来建立标准模型道时要求道集中剩余校正量不能太大,否则会在共反射点道集中引入新误差(Gulunay et al.,2007).考虑到相关性在叠加剖面中要优于存在剩余时差的道集间(夏洪瑞等,1997),因此本文在共反射点道集叠加剖面上建立模型道,得到模型道后的校正方法和传统方法(Gulunay et al.,2007)一致,实现步骤如下.
1)对结构中值滤波后的共反射点道集进行叠加,得到叠加剖面.
2)在叠加剖面上对计算样点所在时窗内进行地层倾向估计,在时窗内取倾向方向中值作为该计算样点的取值.
3)在叠加剖面上,完成一个叠加道的处理即可得到该叠加道对应的共反射点道集的模型道Gm(t,x).
4)对模型道和处理道以最优化方法求校正量函数,得到共反射点道集的剩余校正量模型并沿T方向与X方向做平滑处理,以达到准确求取时移量的目的.
5)对原始道集进行校正处理.
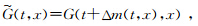
其中,G(t,x)为原始道集,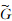 (t,x)为校正后道集,Δm(t,x)为校正量函数.在求取校正量函数过程中,设定的最大允许时移量应随着偏移距的增大而增大;并给定互相关阀值,当互相关值小于阀值则做舍弃处理,以排除由于干扰造成的误差.该方法的优点是:(1)叠加剖面上同相轴相关性优于单道记录,增强了稳定性;(2)当道集中剩余时差较大时,避免了叠加道中引入新的误差;(3)处理前后信号振幅保持不变,保持了AVO特征(刘力辉等,2013).
(t,x)为校正后道集,Δm(t,x)为校正量函数.在求取校正量函数过程中,设定的最大允许时移量应随着偏移距的增大而增大;并给定互相关阀值,当互相关值小于阀值则做舍弃处理,以排除由于干扰造成的误差.该方法的优点是:(1)叠加剖面上同相轴相关性优于单道记录,增强了稳定性;(2)当道集中剩余时差较大时,避免了叠加道中引入新的误差;(3)处理前后信号振幅保持不变,保持了AVO特征(刘力辉等,2013).
基于结构中值滤波的CRP道集优化技术处理流程如图 2所示.为了验证本方法的正确性,选取主频为30 Hz的雷克子波合成含有随机噪声的共反射点道集,采样点数为401,采样率为4 ms,共25道.合成模型中共四个同相轴,作为对比第三个同相轴为完全水平,其余三个同相轴含有不同剩余时差(图 3a).时窗大小取5×5,考虑到同相轴倾向较小,初始系数扫描范围为(-1,1).图 3b为结构中值滤波后道集,对比图 3a可知道集中噪声得到压制,信噪比明显提高.对于理论模型,以同相轴完全水平时道集的叠加作为模型道,对去噪后道集进行剩余量分析和校正,图 4a为道集剩余校正量模型(平滑后),由于第三个同相轴为完全水平,其剩余校正量均为零值,图 4b是对图 3b应用剩余校正量模型校正后的道集.
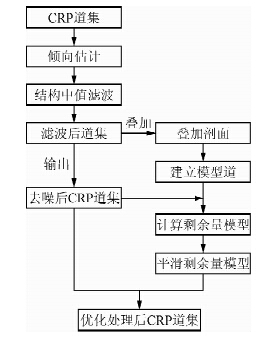 | 图 2 CRP道集优化处理流程图Fig. 2 The flow chart of optimization processing for CRP gather |
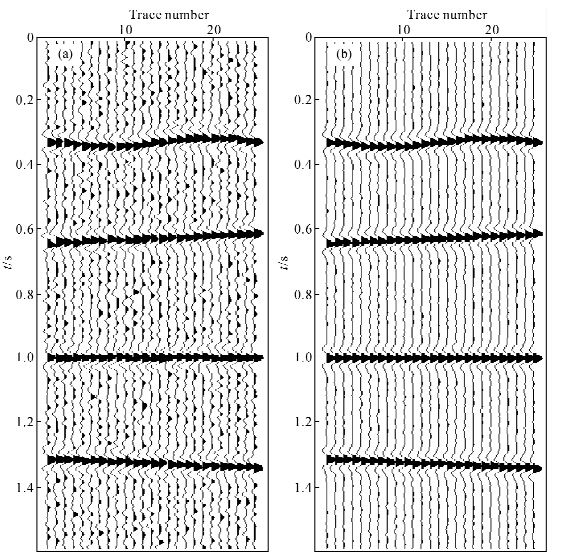 | 图 3 CRP道集模型数据 (a)含有噪声及剩余时差的模型数据;(b)结构中值滤波后道集.Fig. 3 Synthetic data of CRP gather (a)Synthetic data with Residual moveout and noise;(b)After structure median filter. |
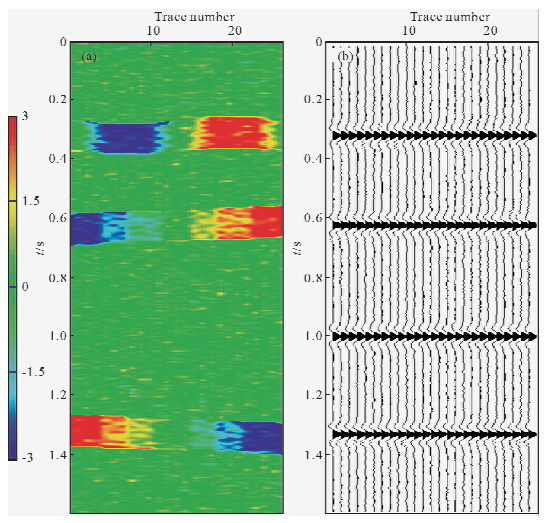 | 图 4 模型数据优化处理后结果 (a)剩余校正量模型;(b)本文方法处理后道集.Fig. 4 The result of optimization processing for Synthetic data (a)Residual moveout map;(b)The gather after flattening with moveout values. |
为了进一步验证本方法的有效性和适用性,选取某实际资料进行试处理并对处理效果进行分析.如图 5a为实际资料的一个共反射点道集(局部),道集中存在噪声干扰和剩余时差,道集叠加不能完全聚焦.选取时窗为7×5,初始系数扫描范围为(-3,3),图 5b为结构中值滤波后结果,在叠加剖面中建立对应CRP道集的参考模型道并对滤波后道集(图 5b)进行优化处理.图 6a为得到的剩余校正量模型,图 6b为校正后道集,原始道集(图 5a)与最终处理道集(图 6b)的对比可知,道集噪声得到压制并且剩余时差被校正,表现为道集被拉平,提高了道集整体质量.图 7为应用本方法处理前后叠加剖面,处理后叠加剖面(图 7b)信噪比得到改善并且同相轴连续性增强,整体剖面质量得到明显提高.叠加剖面的波形变面积显示更清楚地反映了处理前后同相轴的变化,如图 8所示.
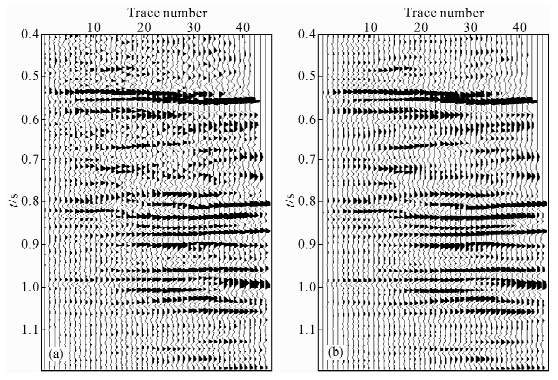 | 图 5 实际CRP道集数据 (a)原始道集;(b)结构中值滤波后道集.Fig. 5 Real data of CRP gather (a)Original data;(b)After structure median filter. |
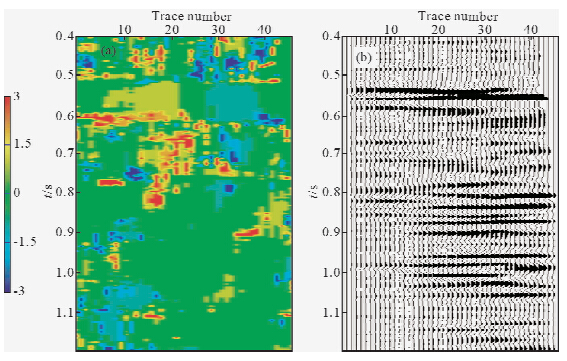 | 图 6 实际数据优化处理后结果 (a)剩余校正量模型;(b)本文方法处理后道集.Fig. 6 The result of optimization processing for Real data (a)Residual moveout map;(b)The gather after flattening with moveout values. |
 | 图 7 实际数据优化处理前后对比剖面 (a)处理前剖面;(b)本文方法处理后剖面.Fig. 7 The real seismic profile (a)Before optimization processing;(b)After optimization processing. |
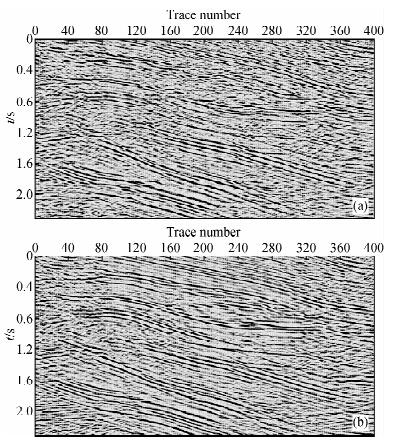 | 图 8 实际数据优化处理前后对比剖面(波形变面积显示) (a)处理前剖面;(b)本文方法处理后剖面.Fig. 8 The real seismic profile shown in wiggle variable area (a)Before optimization processing;(b)After optimization processing. |
共反射点道集对于精确成像和叠前反演具有重要意义,共反射点道集的优化处理中如何提高道集信噪比及剩余时差校正是本文讨论的重点.利用二次多项式拟合地震数据来估计地层倾向是一种简单、有效、可行的途径,由于地层倾向方向具有更强的信息相关性,因此在地层倾向方向运用中值滤波能够得到更好的去噪效果并且可以保护断层边界和不连续性;当共反射点道集品质较差时,简单的道集叠加作为模型道会引入新的误差,考虑到相关性在叠加记录上要好于单道记录,因此可以在叠加剖面上构建模型道,并以相关最优化原则对滤波后道集进行剩余时差校正处理.
本文方法中计算时窗的大小对处理结果有明显影响,增大局部时窗能更好的压制随机噪声,但过大时会导致有效信号的畸变,窗口过小则相关性变差,不利于地层倾向的获得,并且不能有效压制噪声.一般时窗大小取值范围为(5,15)个样点且为奇数;系数的初始值范围应保证扫描到所有可能的倾向,但范围过大则会影响到计算效率,根据地震数据特征一般在(-1,+1)到(-6,+6)范围内进行扫描;求校正量模型时,最大允许时移量应随着偏移距的增大而增大,取值在(3,12)个样点范围内;为了避免相关误差,互相关阀值应在(0.5,0.8)范围内取值.
致 谢 感谢审稿专家提出的宝贵修改意见和编辑部的大力支持.
| [1] | Bakker P. 2002. Image structure analysis for seismic interpretation. PhD Dissertation, Technische Universiteit Delft. |
| [2] | Barnes A E. 2000. Weighted average seismic attributes[J].Geophysics, 65(1): 275-285. |
| [3] | Bednar J B. 1998. Least squares dip and coherency attributes[J]. The Leading Edge, 17(6): 777-778. |
| [4] | Castoro A,White R E, Thomas R D. 2001. Thin-bed AVO: Compensating for the effects of NMO on reflectivity sequences[J].Geophysics, 66(6):1714-1720. |
| [5] | Liu D. 2013a. The effects of Pre-stack seismic data conditioning on AVO analysis[C].//83th Annual International Meeting, SEG, Expanded Abstracts, 452-456. |
| [6] | Liu Y K. 2013b. Noise reduction by vector median filtering[J]. Geophysics, 78(3): 79-86. |
| [7] | Dunkin J W, Levin F K. 1973. Effect of normal moveout on a seismic pulse[J].Geophysics, 28(4):635-642. |
| [8] | Eichkitz C G,Amtmann J,Schreilechner M G. 2012. Enhanced coherence attribute imaging by structurally oriented filtering[J]. First Break, 30(3):75-81. |
| [9] | Fehmers C C, Höcker C F W. 2002. Fast structural interpretation with structure-oriented filtering[J]. The Leading Edge, 21(3): 238-243. |
| [10] | Gersztenkorn A,Marfurt K J. 1999. Eigenstructure-based coherence computations as an aid to 3-D structural and stratigraphic mapping[J]. Geophysics, 64(5): 1468-1479. |
| [11] | Gulunay N, Magesan M, Roende H H. 2007a. Gather flattening[J]. The Leading Edge,26(12): 1538-1543. |
| [12] | Gulunay N, Gamar F, Hoeber H, et al. 2007b. Robust residual gather flattening[C].//77th Annual International Meeting, SEG, Expanded Abstracts, 229-233. |
| [13] | Hinkley D,Bear G W, Dawson C. 2004. Prestack gather flattening for AVO[C].//74th Annual International Meeting, SEG, Expanded Abstracts, 271-273. |
| [14] | Lazaratos S, Finn C. 2004. Deterministic spectral balancing for high-fidelity AVO[C].// 74th Annual International Meeting, SEG, Expanded Abstracts, 219-223. |
| [15] | Luo Y, Higgs W G,Kowalik W S. 1996. Edge detection and stratigraphic analysis using 3D seismic data[C].//SEG, Expanded Abstracts, 324-327. |
| [16] | Luo Y, Marhoon M, Al Dossary S, et al. 2002. Edge-preserving smoothing and applications[J]. The Leading Edge, 21(2): 136-158. |
| [17] | Marfurt K J, Kirlin R L, Farmer S L, et al. 1998. 3-D seismic attributes using a semblance-based coherency algorithm[J]. Geophysics, 63(4): 1150-1165. |
| [18] | Pérez G, Marfurt K. 2006. Correcting for wavelet stretch in common-angle migration improves vertical and lateral resolution[C].//76th Annual International Meeting,SEG, Expanded Abstracts, 254-257. |
| [19] | Roy B,Anno P,Baumel R, et al. 2005. Analytic correction for wavelet stretch due to imaging[C].//75th Annual International Meeting, SEG, Expanded Abstracts, 234-237. |
| [20] | Singleton S. 2009. The effects of seismic data conditioning on prestack simultaneous impedance inversion[J]. The Leading Edge, 28(1): 260-267. |
| [21] | Swan H W. 2001. Velocities from amplitude variations with offset[J].Geophysics, 66(6): 1735-1743. |
| [22] | 程玉坤,冉建斌,肖伟.2008.基于CRP道集的叠前处理技术及应用[J].勘探地球物理进展,31(1):38-43. |
| [23] | 高静怀,毛剑,满蔚仕,等.2006.叠前地震资料噪声衰减的小波域方法研究.地球物理学报,49(4): 1155-1163. |
| [24] | 林伯香,孙建国.2001.相位替换法剩余时差校正.石油物探,40(3):15-22. |
| [25] | 李钟晓,陆文凯,王季.2013.基于地震图像校准的共成像点道集增强技术.地球物理学报,56(5):1592-1608. |
| [26] | 李月,杨宝俊,赵雪平,等.2005.检测地震勘探微弱同相轴的混沌振子算法.地球物理学报,48(6):1428-1433. |
| [27] | 刘力辉,杨晓,丁燕,陆蓉,康昆.2013.基于岩性预测的CRP道集优化处理[J].石油物探,5(5):482-488. |
| [28] | 刘振,张军华,韩双,等.2013.CRP道集局部校正与去噪方法.地球物理学进展,28(6):3092-3097. |
| [29] | 王开燕,李慧,官波,等.2007.相位剩余时差校正方法在提高分辨率中的应用.大庆石油学院学报,31(6): 14-17. |
| [30] | 王旭松,杨长春.2006.对地震图像进行保边滤波的非线性各向异性扩散算法.地球物理学进展, 21(2):452-457. |
| [31] | 王伟,高静怀,陈文超等.2012.基于结构自适应中值滤波器的随机噪声衰减方法.地球物理学报, 55(5): 1732-1741. |
| [32] | 王云专,杨立伟,李素华.2006.剩余时差校正及泊松比反演.地球物理学进展,21(1):214-218. |
| [33] | 夏洪瑞,陈德刚,周开明.1997.剩余动校正量的拾取与消除.石油地球物理勘探,32(6):872-877. |
| [34] | 夏洪瑞,董江伟,邹少峰,刘艳峰.2006.常规二次多项式拟合地震数据[J].石油物探,45(5):492-496. |
| [35] | 俞寿朋.1993.高分辨率地震勘探[M].北京:石油工业出版社,142-145. |
| [36] | 杨培杰,穆星,张景涛.2010.方向性边界保持断层增强技术.地球物理学报,53(12):2992-2997. |
| [37] | 张尔华,王伟,高静怀,等.2010.非线性各向异性扩散滤波器用于三维地震资料噪声衰减与结构特征增强.地球物理学进展,25(3):866-870. |
| [38] | 张军华,吕宁,田连玉,等.2006.地震资料去噪方法技术综合评述[J].地球物理学进展,21(2):546-553. |
| [39] | 张征,狄帮让,胡英,姚逢昌.2012.CRP道集叠前精细处理技术应用.科技导报,30(27),35-40. |
 2015, Vol. 30
2015, Vol. 30

