阿尔奇公式作为连接电阻率与孔隙度、饱和度之间的桥梁,从半个多世纪的应用实践中证明了其正确性,同时,也表现出其存在的局限性和不足.Etris等在用岩相法分析阿尔奇公式适应性时指出,仅在一些非常有限的岩石类型中才能满足阿尔奇公式的简单函数(李宁,2013).在一般应用中,人们通常是根据现场实际情况对阿尔奇公式中的参数(a,b,m和n)取经验值来使用,但是对碳酸盐岩而言,由于其储层强烈的非均质性,如果直接利用固定的阿尔奇参数,其计算结果会存在极大的误差.因此许多学者对能应用于缝洞型储层中的孔隙度指数m做了大量的研究(Towle,1962;Aguilera,1976;曾文冲,1979;Rasmus,1983;Draxler and Edwards,1984;Serra,1989;Maria and Roberto,2003;Aguilera,2004;蒋进勇,2004;Berg,2006;Aguilera,2010;Al-Ghamdi et al,2010;徐炳高等,2011;覃豪等,2011;赵辉等,2012).Towle在考虑孔隙几何形态(如弯曲度)的情况下,通过理论模型的推导认为,对于孔洞型储层,孔隙度指数m一般从2.67至7.3+变化,而对于裂缝型储层,孔隙度指数m要小于2;Aguilera介绍了一种能处理基质和裂缝孔隙的双孔隙模型,他考虑了三种不同的Archie孔隙度指数:基质孔隙度指数(mb)、裂缝孔隙度指数(mf)和两者组合的系统孔隙度指数(m);曾文冲给出了孔隙度指数m的物理意义,他认为孔隙度指数m与储层的孔隙结构密切相关,可表示为渗透率和孔隙度二者的函数,且更大程度受上受控于渗透率,对于裂缝性储层,由于高渗透率的特征,其m值相对较小;Rasmus和Draxler及Edwards提出的双孔隙模型,考虑了裂缝弯曲度和裂缝孔隙度指数的改变,但是该模型在随着总孔隙度的增加,会出现总孔隙度指数(m)大于基质孔隙度指数(mb)的错误;Serra等建立了适合具有裂缝和非连通缝洞的储层的模型,并给出了孔隙度指数(m)与总孔隙度(Ф)的关系图版,但是对于基质和非连通缝洞的某些组合,该模型会出现明显的错误;Aguilera等在2003年通过严格的公式推导,提出了适用于基质、裂缝和非连通缝洞任意组合的双孔隙模型;Aguilera在原有双孔隙模型研究的基础之上提出了一种三孔隙度模型,该模型适用于基质、裂缝和不连通孔洞同时存在的情况.然而上述模型都是在电流流向与裂缝平行的假设条件下建立的;Berg在Aguilera的三孔隙度模型基础上,基于有效介质理论给出了新的三孔隙度模型,该模型考虑了裂缝方位等问题;Aguilera在2009年提出了考虑裂缝倾角和裂缝弯曲度的孔隙度指数计算模型,但在现实中,准确获取裂缝倾角和裂缝弯曲度存在一定的困难;Al-Ghamdi等在2010年对Aguilera提出的三孔隙度模型进行了改进,在考虑了基质、裂缝和孔洞的情况下,进行了严格的理论推导,给出了改进的三孔隙度模型.
虽然未改进的三孔隙度模型现已被解释人员大量应用于生产实践中,其也取得了一定的应用效果(漆立新等,2010;张丽华等,2008;应海玲等,2010;张丽华等,2010;刘瑞林等,2009;冯周等,2011;潘保芝等,2006),但是通过与改进后的三孔隙度模型对比会发现,未改进的模型在某些情况下仍存在较大的误差.本文通过对三孔隙度模型中影响孔隙度指数的各种影响因素的分析,直观地给出了改进前后的三孔隙度模型存在的差异.理论研究表明,改进后的三孔隙度模型比未改进的三孔隙度模型更加符合实际情况.
1 改进前后的三孔隙度模型在缝洞型储层中,基质、裂缝和孔洞同时存在的情况非常普遍,三孔隙度模型就是为了解决这类复杂储层而提出的.不管是未改进还是改进后的三孔隙度模型(图 1),其核心思想都是认为地层中基质孔隙与裂缝并联导电,把其作为一个整体后再与非连通缝洞串联导电(式1),所以两个模型从本质上没有很大的区别.其具体区别是,在考虑基质孔和裂缝组成的复合系统中,对于复合系统的电阻率的求取上存在差异.未改进的三孔隙度模型在考虑基质和裂缝组合的系统时,把基质和裂缝重新当做一个整体(没有考虑非连通缝洞部分)(式2,3),而改进的三孔隙度模型在考虑基质和裂缝的复合系统时,它并没有把基质和裂缝当做一个整体(考虑了非连通缝洞部分)(式4,5).所以虽然都经过相同的理论推导,但这两个模型还是存在明显的区别(式6,7).
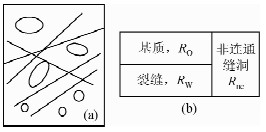 | 图 1 (a)缝洞型储层储集空间示意图;(b)三孔隙度模型示意图Fig. 1 (a)schematic of reservoir space;(b)schematic of tripe porosity model |

未改进的三孔隙度模型为
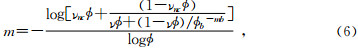
改进后的三孔隙度模型为
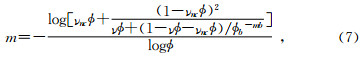
其中,m—缝洞型储层的孔隙度指数;Ф—总孔隙度,小数;Фnc—非连通缝洞孔隙度,小数;Фb—基质孔隙度,小数;Ф2—裂缝孔隙度,小数;mb—基质部分的孔隙度指数;νnc=Фnc/Ф;ν=Ф2/Ф;Rfnco—在储层温度时,当100%饱和电阻率为Rw水时,复合系统的电阻率,Ω·m;Rw—地层温度下地层水电阻率,Ω·m;Ro—在储层温度时,当100%饱和电阻率为Rw水时,基质系统的电阻率,Ω·m;Rfo—在储层温度时,当100%饱和电阻率为Rw水时,由基质和裂缝组成的系统的电阻率,Ω·m.
通过观察改进前后的三孔隙度模型可以发现,缝洞型储层的孔隙度指数与储层的基质孔隙度、裂缝孔隙度、非连通缝洞孔隙度以及基质孔隙度指数都有关系.为了更好的了解各种参数对改进前后的三孔隙度模型求取复合孔隙度指数m的影响情况,下面通过这些影响因素来对比研究改进前后的模型的区别以及缝洞型储层孔隙度指数的变化规律.
2 孔隙度指数变化规律 2.1 孔隙度指数与非连通缝洞孔隙度、基质孔隙度指数的关系在基质孔隙度、裂缝孔隙度和总孔隙度一定的情况下,复合系统的孔隙度指数m随着非连通缝洞孔隙度Фnc的增大而增大,且改进前后的模型之间存在一定的差异(图 2).可以发现,当总孔隙度小于0.2时,改进前后的模型差异不大,但当总孔隙度大于0.2后,两种模型所求得的复合系统孔隙度指数是存在明显不同的.虽然在基质孔隙度、裂缝孔隙度和基质孔隙度指数一定的情况下,改进前后的三孔隙度模型求得的复合系统孔隙度指数m都是随着非连通缝洞孔隙度Фnc(Фnc=Ф-Ф2 -Фm)的增加而逐渐增大的,但是改进后的三孔隙度模型求得的m值相对改进前的三孔隙度模型要小.而且在基质孔隙度、裂缝孔隙度和非连通缝洞孔隙度一定时,复合系统的孔隙度指数m随着基质孔隙度指数mb的增大也是逐渐增大的.
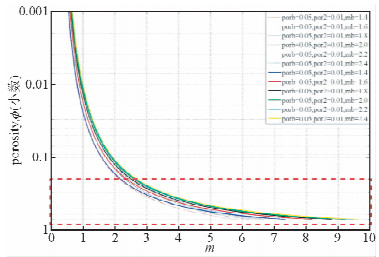 | 图 2 改进前后的三孔隙度模型求得的孔隙度指数m与非连通缝洞Фnc、基质孔隙度指数mb之间的关系(其中虚线代表改进后的模型,实线代表未改进的模型,porb代表基质孔隙度,por2代表裂缝孔隙度)Fig. 2 The relationship between porosity exponent mcalculated by tripe porosity model before and after improvement and non-connected vugs Фnc,matrix porosity exponent mb.(the dotted line represent the improved model,the solid line represent the unimproved model,porb represents matrix porosity,por2 represents fracture porosity) |
在裂缝孔隙度、非连通缝洞孔隙度和基质孔隙度指数一定的情况下,复合系统的孔隙度指数m随着基质孔隙度Фb(Фb=(Ф-Ф2-Фnc)/(1-Ф2-Фnc))的增加而出现先增大后减小的现象,最终减小至与基质孔隙度指数相同(见图 3).在图 3中可以发现,随着基质孔隙度的增加,改进前后的三孔隙度模型求得的复合系统孔隙度指数有着相同的变化趋势,但是当m值增大到最大值附近时,两种模型求得的m值存在明显的区别,如图 3,当总孔隙度Ф在6%至30%之间时,两种模型之间的差异是显而易见的.
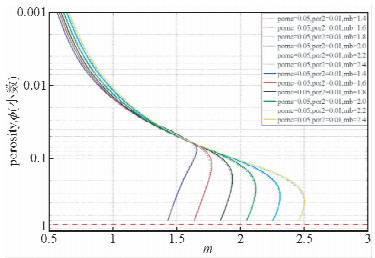 | 图 3 改进前后的三孔隙度模型求得的孔隙度指数m与基质孔隙度Фb之间的关系(虚线代表改进后的模型,实线代表未改进的模型,por2代表裂缝孔隙度,pornc代表非连通缝洞孔隙度) Fig. 3 The relationship between porosity exponent mcalculated by tripe porosity model before and after improvement and matrix porosity Фb.(the dotted line represent the improved model,the solid line represent the unimproved model,por2 represents fracture porosity,pornc represents non-connected vugs porosity) |
在图 3中,当总孔隙度、裂缝孔隙度和非连通缝洞孔隙度都一定的情况下,对比mb=1.6、1.8、2.0、2.2、2.4所对应的复合系统孔隙度指数m随总孔隙度的变化曲线(考虑Ф≥Фnc+Ф2所对应的曲线部分)可以发现,任意两曲线之间的孔隙度指数m的差值随着总孔隙度的变大均有增大的趋势.
2.3 孔隙度指数与裂缝孔隙度的关系在基质孔隙度、非连通缝洞孔隙度和基质孔隙度指数一定的情况下,复合系统孔隙度指数m随着裂缝孔隙度Ф2的增加而逐渐减小(只考虑Ф≥Фnc+Фb所对应的曲线部分)(见图 4).通过图 4a、b、c、d的对比研究发现,复合系统孔隙度指数m的变化是存在一定规律的.
由图 4a可以发现,当基质孔隙度、非连通缝洞孔隙度和基质孔隙度指数一定时,复合系统孔隙度指数m随着裂缝孔隙度Ф2的增加而逐渐减小.通过对比改进前后的三孔隙度模型,当总孔隙度小于0.4左右时,两种模型求得的孔隙度指数m随总孔隙度的变化趋势几乎相同,但当总孔隙度大于0.4时,改进前后的模型就有比较明显的差异,且随着总孔隙度的增加,差异越来越大,这种现象在图 4b、c、d上都有表现.
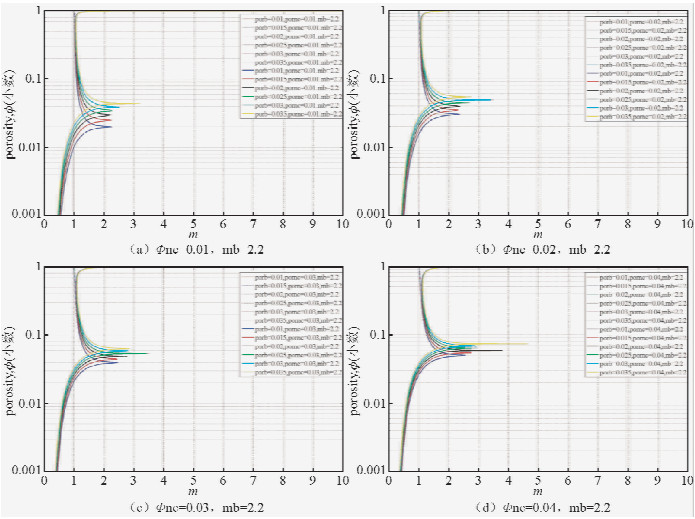 | 图 4 改进前后的三孔隙度模型求得的孔隙度指数m与裂缝孔隙度Ф2之间的关系(虚线代表改进后的模型,实线代表未改进的模型,porb代表基质孔隙度,pornc代表非连通缝洞孔隙度)Fig. 4 The relationship between porosity exponent m calculated by tripe porosity model before and after improvement and fracture porosity Ф2.(the dotted line represent the improved model,the solid line represent the unimproved model,porb represents matrix porosity,pornc represents non-connected vugs porosity) |
在图 4a中,当Фnc=0.01,Фb=0.01,mb=2.2时,可以发现复合系统孔隙度指数m的最大值出现在总孔隙度Ф=0.02处;在图 4b中,当Фnc=0.02,Фb=0.01,mb=2.2时,复合系统孔隙度指数m的最大值出现在总孔隙度Ф=0.03处; 同理在图 4c中,复合系统孔隙度指数m的最大值出现在总孔隙度Ф=0.04处,在图 4d中,复合系统孔隙度指数m的最大值出现在总孔隙度Ф=0.05处.因此可以看出,当总孔隙度=基质孔隙度+非连通缝洞孔隙度时(Ф=Фnc+Фb),复合系统孔隙度指数m达到最大值,但随着裂缝的发育,其孔隙度指数m会逐渐减小.例如:当Ф=0.025,Фb=0.015,Фnc=0.01,mb=2.2时,孔隙度指数m达到的最大值为2.2446,而当Ф=0.03,Фb=0.015,Фnc=0.01,mb=2.2时,孔隙度指数m就立刻减小至1.4873.而且我们还可以发现,随着裂缝孔隙度的增加,复合系统孔隙度指数m变化率也是逐渐减小的.
在图 4a中,对比改进前后的三孔隙度模型可以发现,当Фnc=0.01,Ф≥0.7时,两种模型存在明显差异;在图 4b中,当Фnc=0.02,Ф≥0.6时,两种模型存在明显差异;同理在图 4c、d中,当Фnc=0.03,Ф≥0.5和Фnc=0.04,Ф≥0.4时,两种模型均存在明显差异.因此可以看出,在相同的条件下,随着非连通缝洞体积占储层总体积比重的增大,两种模型存在明显差异的总孔隙度界限值也越来越低.所以对于缝洞发育的碳酸盐岩储层而言,当储层的非连通缝洞很发育时,利用未改进的三孔隙度模型去计算复合系统孔隙度指数是存在很大误差的.
通过以上各种影响因素的分析可以看出,每个因素对复合系统孔隙度指数都有着很大的影响,而且改进前后的三孔隙度模型受每个因素的影响程度也不尽相同,其中改进后的三孔隙度模型求取的复合系统孔隙度指数随各个因素的变化规律更符合人们的认识.
3 改进前后的三孔隙度模型的应用对比本文采用来自中东碳酸盐岩储层的两个岩心样品的数据(数据源于Al-Ghamdi et al,2010)对改进前后的三孔隙度模型进行应用对比.岩样1是形成于晚侏罗纪的鲕粒灰岩,储集空间主要是粒间孔,并伴随有一些粒内孔和铸模孔,铸模孔和微裂缝占总孔隙度的比重很少;岩样2是形成于晚侏罗纪的微晶质粒泥灰岩,主要的颗粒是微晶化的球粒和孔虫类及生物碎屑的骨粒,主要储集空间为窗格孔,粒间孔、粒内孔和裂缝大约占总孔隙的10%.其中,岩样1取自油层段,而岩样2取自水层段.具体数据见表 1,其中裂缝孔隙度Ф2通过岩心及成像测井资料获得;总孔隙度Ф通过常规测井及核磁测井获得;基质孔隙度Фb通过缝洞不发育的层段获得;非连通缝洞孔隙度Фnc利用三孔隙度模型计算获得.在应用三孔隙度模型时,我们认为饱和度指数n与复合系统孔隙度指数m相等.
| 表 1 碳酸盐岩储层中三孔隙度模型的应用Table 1 The application of tripe porosity model in carbonate reservoirs |
将改进后的三孔隙度模型应用于岩样1,我们可以得到复合系统的孔隙度指数m为2.1275,含水饱和度为36.32%;而将未改进的三孔隙度模型应用到岩样1时,求得的复合系统孔隙度指数m为3.2352,含水饱和度高达89.14%.同理将改进前后的三孔隙度模型分别应用到岩样2时,我们发现改进后的模型求得的m为2.6184,含水饱和度为98.98%,而未改进的模型求得的m为2.6707,含水饱和度为103.19%,这明显是错误的.
通过上述应用可以发现,改进前后的三孔隙度模型在相同的条件下求取的孔隙度指数m和含水饱和度Sw是存在明显差异的,其中改进前的模型与实际岩心分析情况存在很大的误差,其判断的结果与实际情况明显不符;而改进后的三孔隙度模型计算的结果与实际情况有较好的吻合,更符合实际情况.
为了更好地理解孔隙度指数的差值Δm(改进后的三孔隙度模型计算的孔隙度指数与未改进的三孔隙度模型计算的孔隙度指数差值的绝对值)对饱和度的影响,我们假设地层真电阻率Rt=20 Ω·m,地层水电阻率Rw=0.01 Ω·m,复合系统真实的孔隙度指数为2.0,总孔隙度Ф分别取0.1、0.15、0.2、0.25等值,从而来研究错误的含水饱和度(改进前模型计算的含水饱和度减去改进后模型计算的含水饱和度)与孔隙度指数差值Δm之间的关系,如图 5所示.
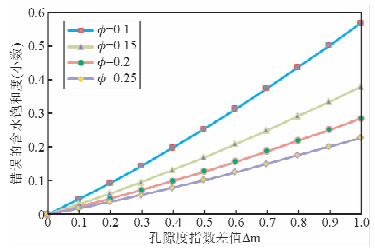 | 图 5 错误的含水饱和度Sw与孔隙度指数差值Δm的关系Fig. 5 The relationship between error water saturation Sw and difference of porosity exponent Δm |
从图 5可以发现,当计算的孔隙度指数m与实际的孔隙度指数存在差异的时候,其对所计算的饱和度存在很大的影响,而且随着Δm的增大,计算的含水饱和度的错误值也越来越大,其直接的后果就是导致解释人员对储层流体性质判断错误.而且我们还发现,在Δm一定的时候,随着总孔隙度的减小,计算的含水饱和度的错误值相对而言将增大.
以上的应用分析可以看出,改进后的三孔隙度模型计算的结果与实际情况有较好的吻合,而未改进的三孔隙度模型计算的结果存在较大误差.而且孔隙度指数m计算的准确与否对准确求取饱和度有着很大的影响.
4 结 论4.1 虽然改进前后的三孔隙度模型均适用于基质、裂缝和孔洞发育的储层,但是未改进的三孔隙度模型有时会存在很大的误差,甚至是出现错误,而改进后的三孔隙度模型更加符合实际情况.
4.2 通过对复合系统孔隙度指数的影响因素的分析可知,基质孔隙度、裂缝孔隙度、非连通孔洞孔隙度和基质孔隙度指数对复合系统孔隙度指数都有影响.其中,基质孔隙度指数的增大会导致复合系统的孔隙度指数变大;基质孔隙度的增加会使复合系统的孔隙度指数先增大后减小,并逐渐接近于基质孔隙度指数;裂缝孔隙度的增加会导致复合系统的孔隙度指数减小,并逐渐接近于1;非连通缝洞孔隙度的增加会使复合系统的孔隙度指数增大.
4.3 孔隙度指数求取的准确与否对准确求取饱和度有着至关重要的影响,利用改进后的三孔隙度模型计算的结果更加准确可靠.
4.4 将改进后的三孔隙度模型计算的复合系统孔隙度指数代入阿尔奇公式来计算缝洞型储层的饱和度可以提高饱和度的计算精度.
致 谢 感谢中国石油勘探开发研究院测井与遥感技术研究所周灿灿所长对本文提出的修改意见和给予的支持!
| [1] | Al-Ghamdi A, Chen B, Behmanesh H, et al. 2010. An improved triple-porosity model for evaluation of naturally fractured reservoirs[C].//SPE-132879-PA SPE Reservoir Evaluation & Engineering. |
| [2] | Feng Z, Liu R L, Ying H L, et al. 2011. Comparison of fracture-vuggy porosity and logging data interpretation in CT image segmentation[J]. Journal of Oil and Gas Technology(J. JPI)(in Chinese), 33(4):100-104. |
| [3] | Jiang J Y. 2004. The porosity interpretation model for carbonate reservoir in Tahe oilfield[J]. Geophysical Prospecting for Petroleum (in Chinese), 43(6):564-567. |
| [4] | Li N. 2013. Introduction to Logging Interpretation of China Marine Carbonate Rocks (in Chinese)[M]. Beijing:Science Press. |
| [5] | Liu R L, Fan Z J, Liu J H. 2009. A method of project mapping for correcting mud invasion and calculating apparent formation-water resistivity and water saturation[J]. Journal of Oil and Gas Technology (J. JPI) (in Chinese), 31(6):104-107, 118. |
| [6] | Maria S A, Roberto A. 2003. Improved models for petrophysical analysis of dual porosity reservoirs[J]. Petrophysics, 44(1):21-35. |
| [7] | Pan B Z, Zhang L H, Shan G Y, et al. 2006. Progress in porosity model for fractured and vuggy reservoirs[J]. Progress in Geophysics (in Chinese), 21(4):1232-1237, doi:10.3969/j.issn.1004-2903.2006.04.028. |
| [8] | Qi L X, Fan Z J, Li Z J, et al. 2010. Tri-porosity logging model of carbonate reservoir in Tahe Oilfield and its application[J]. Geophysical Prospecting for Petroleum (in Chinese), 49(5):489-494. |
| [9] | Qin H, Li H J, Yang X F, et al. 2011. A study on the fluid identification method of acidic volcanic reservoirs based on the pore structure[J]. Chinese J. Geophys. (in Chinese), 54(2):422-427, doi:10.3969/j.issn.0001-5733.2011.02.019. |
| [10] | Rasmus J C. 1983. A variable cementation exponent, M, for fractured carbonates[J]. The Log Analyst, 24(6):13-23. |
| [11] | Roberto F A, Roberto A. 2004. A triple porosity model for petrophysical analysis of naturally fractured reservoirs[J]. Petrophysics, 45(2):157-166. |
| [12] | Roberto A. 2010. Effect of fracture dip and fracture tortuosity on petrophysical evaluation of naturally fractured reservoirs[J]. Journal of Canadian Petroleum Technology, 49(9):69-76. |
| [13] | Serra O. 1989. Formation Microscanner Image Interpretation[M]. Houston:Schlumberger Educational Services, SMP-7028, 117. |
| [14] | Towle G. 1962. An analysis of the formation resistivity factor-porosity relationship of some assumed pore geometries[C].//Houston, Texas:Third Annual Meeting of SPWLA. |
| [15] | Xu B G, Li Y B, Dong Z. 2011. Determination method for m and n parameters of marine carbonate saturation in northeast Sichuan[J]. Well Logging Technology (in Chinese), 35(1):51-54. |
| [16] | Ying H L, Ouyang M, Liu R L, et al. 2010. A verfication of the cementation exponent calculated by triple porosity model in volcanic reservoir[J]. Well Logging Technology (in Chinese), 34(6):559-563. |
| [17] | Zhang L H, Pan B Z, Shan G Y. 2008. Tri-porosity model and its application in igneous reservoir[J]. Well Logging Technology (in Chinese), 32(1):37-40. |
| [18] | Zhang L H, Pan B Z, Shan G Y. 2010. Progress in study on methods of determining porosity exponent m[J]. Progress in Geophysics (in Chinese), 25(3):975-981, doi:10.3969/j.issn.1004-2903.2010.03.036. |
| [19] | Zhao H, Shi X, Sima L Q. 2012. Study on porosity exponent, saturation and fracture porosity for fractured reservoirs[J]. Progress in Geophysics (in Chinese), 27(6):2639-2645, doi:10.6038/j.issn.1004-2903.2012.06.043 |
| [20] | 冯周,刘瑞林,应海玲,等. 2011.岩心CT扫描图像分割计算缝洞孔隙度与测井资料处理结果对比研究[J].石油天然气学报(江汉石油学院学报), 33(4):100-104. |
| [21] | 蒋进勇. 2004.塔河油田碳酸盐岩储层孔隙度模型的改进[J].石油物探, 43(6):564-567. |
| [22] | 李宁. 2013.中国海相碳酸盐岩测井解释概论[M].北京:科学出版社. |
| [23] | 刘瑞林,樊政军,柳建华. 2009.一种校正泥浆侵入影响计算视地层水电阻率与含水饱和度的投影作图方法[J].石油天然气学报(江汉石油学院学报), 31(6):104-107, 118. |
| [24] | 潘保芝,张丽华,单刚义,等. 2006.裂缝和孔洞型储层孔隙模型的理论进展[J].地球物理学进展, 21(4):1232-1237, doi:10.3969/j.issn.1004-2903.2006.04.028. |
| [25] | 漆立新,樊政军,李宗杰,等. 2010.塔河油田碳酸盐岩储层三孔隙度测井模型的建立及其应用[J].石油物探, 49(5):489-494. |
| [26] | 覃豪,李洪娟,杨学峰,等. 2011.基于孔隙结构的酸性火山岩储层流体识别方法研究[J].地球物理学报, 54(2):422-427, doi:10.3969/j.issn.0001-5733.2011.02.019. |
| [27] | 徐炳高,李阳兵,董震. 2011.川东北海相碳酸盐岩饱和度参数m、n确定方法[J].测井技术, 35(1):51-54. |
| [28] | 应海玲,欧阳敏,刘瑞林,等. 2010.三孔隙度模型计算胶结指数在火山岩储层中的验证[J].测井技术, 34(6):559-563. |
| [29] | 曾文冲. 1979.孔隙结构指数m的物理意义及其表达式[J].测井技术, (5):6-14. |
| [30] | 张丽华,潘保芝,单刚义. 2008.应用三重孔隙模型评价火成岩储层[J].测井技术, 32(1):37-40. |
| [31] | 张丽华,潘保芝,单刚义. 2010.孔隙度指数m确定方法研究进展[J].地球物理学进展, 25(3):975-981, doi:10.3969/j.issn.1004-2903.2010.03.036. |
| [32] | 赵辉,石新,司马立强. 2012.裂缝性储层孔隙指数、饱和度及裂缝孔隙度计算研究[J].地球物理学进展, 27(6):2639-2645, doi:10.6038/j.issn.1004-2903.2012.06.043. |
 2015, Vol. 30
2015, Vol. 30

