2. 中煤科工集团西安研究院有限公司, 西安 710077
2. China Coal Research Institute Xi'an Science and Industry Group, Xi'an 710077, China
随着非常规油气和煤层气的大规模勘探开发,水平井技术已成为油气勘探中一种不可缺少的技术.水平井的环境不同于垂直井,主要表现在井眼、空间位置、地层的非均质性等方面.水平井中重力与井轴的方向相互垂直,以及井位置的多变性使井下流动状态与垂直井的情况极不相同,造成常规测井仪器在水平井中性能指标下降、导致测井解释异常复杂化,因此对水平井中的地层进行感应测井正演数值模拟,分析各种因素的影响是十分必要的.
对于感应测井数值模拟,近些年由于感应测井可以在不导电的油基泥浆或空气钻孔内测定岩层电阻率的特有优势受到越来越多的关注与重视.早期的感应测井响应数值模拟研究基本上都是基于几何因子理论(Doll,1949;Moran,1982),没有考虑到地层非均质界面等因素对电磁场的影响;之后,在考虑了发射和接收线圈的尺寸,顾及井眼影响的情况下,利用交错网格有限差分方法计算了三维感应测井响应(汪功礼等,2003);后来又对阵列感应测井的有限元正演方法在垂直井中的应用进行了一定研究(仵杰等,2008);高分辨率阵列侧向测井的等值面边值问题模型可大大缩小求解区域而不影响计算精度,但实现起来较为繁琐(潘克家等,2013).
COMSOL Multiphysics为基于有限元方法以及多物理场耦合分析的标准工具,在全球500强企业中被视作提升核心竞争力,增强创新能力,加速研发的重要工具.本文利用COMSOL有限元软件建立三层对称地层模型,对水平井感应测井响应影响因素进行数值模拟.分别分析了仪器位置、上下围岩电导率、目的层厚度、仪器偏心对感应测井响应的影响.数值模拟结果不仅可指导水平井感应测井资料解释进而提供校正图版而且对感应测井仪器的研发工作提供了理论依据.
1 描述感应测井电磁场的基本 PDE 方程COMSOL Mutiphysics 是一款功能强大的解决多物理场问题的有限元数值计算软件.它以有限元方法为基础,通过求解偏微分方程或偏微分方程组来实现物理现象的模拟仿真,实现物理问题向数学问题的转换.
感应测井中,发射的电流都是交流电,在周围地层空间中产生的场将是时谐电磁场.时谐电磁场的麦克斯韦方程组为
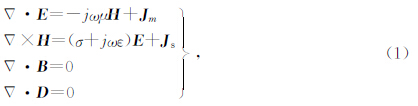
感应测井中,线圈的尺寸与线圈间的距离相比是很小的,因此可以把发射源等效为振荡的磁偶极子源,即为式(1)中的Jm.把发射源等效为磁偶极子源,这样在几何建模时就可以用一个点来代替仪器的发射线圈,大大简化了几何模型.随钻感应测井的线圈系由一个发射线圈和两个接收线圈构成,其线圈轴与井轴平行,则发射源是垂直磁偶极子源,大小为MS=ITNTπa2T,其中IT是电流强度,NT为发射线圈匝数,aT是发射线圈的半径.COMSOL三维有限元数值计算软件,可以求出当发射源为垂直磁偶极子源时地层中的电磁场分布,即Hx、Hy、Hz、Ex、Ey、Ez.在建模时,不建立接收线圈模型,直接计算出在三维模型中接收线圈所在位置的电磁场.
使用COMSOL软件进行数值计算直接得到的是地层周围的电场和磁场的各个分量,而在实际测井中,直接测量到的是接收线圈处的的感生电动势,所以需要对计算的结果进行处理,把电场或磁场转化为电动势.在直角坐标系下,接收线圈处的感生电动势处理方法为

视电导率的表达式为

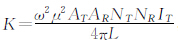 ,K定义为仪器的仪器常数,如果线圈系频率ω给定,K则为常数.Vm定义为直耦电动势,它的大小为:线圈系置于电导率σ=0的空气中时发射电流在接收线圈中直接产生的电动势.
,K定义为仪器的仪器常数,如果线圈系频率ω给定,K则为常数.Vm定义为直耦电动势,它的大小为:线圈系置于电导率σ=0的空气中时发射电流在接收线圈中直接产生的电动势.
Comsol的AC/DC模块提供的一般形式的偏微分方程为

另外,本文边界条件设置为“连续”,边缘条件设置为“磁绝缘”.
2 三层对称地层模型的建立三层对称地层模型属于三维的地层模型,有限元网格剖分比较复杂,网格处理不得当就不能得到准确的计算结果.因而必须对感应测井仪器周围的地层区域进行加密剖分来提高计算的精度,这里采用 COMSOL 提供的分块区域加密的方法进行处理,这是一种牺牲速度来提高精度的做法.所建的三维模型如图 1a所示,简单的做法是在井眼的周围加了一个六面体,使得六面体的长、宽、高稍大于目的层厚度的尺寸,即超过目的层与围岩的交界面,达到使网格连续的目的.该六面体关于井轴心对称,并且其内的网格单元剖分会比地层中的其它区域密集.图 1b是网格剖分的效果图,本文采用的是四面体网格剖分.可以看出,井眼的网格比六面体单元的网格密,而六面体内的网格比其它围岩的网格密.
 |
图 1 三层对称地层的三维模型与网格剖分结果 (a)三层对称地层的三维模型; (b) 三层对称地层模型网格剖分. Fig. 1 3D model and the grid subdivision of three layer symmetric formation (a)3D model of three layer symmetric formation; (b) Three layer symmetric formation model’s grid subdivision. |
在三层对称地层模型中,仪器和井眼在地层中上下可移动,仪器距离上下围岩距离不同其测量的视电导率值一般也是不同的.选取传播频率为20 kHz,在不考虑仪器偏心和泥浆侵入的情况下,依据图 1a的三层对称地层模型,建立目的层厚ht=2 m,上下围岩厚度hs=5 m,目的层电导率σt=1 S/m,上下围岩的电导率σs=10 S/m,泥浆电导率σm=2 S/m,井径为8 in(0.2032 m),目的层中心位于xoy面内.
取仪器距离下围岩分别从 0.2 m 到 1.8 m 以 0.2 m 为步长增长的一系列位置分析对视电导率的影响.
从图 2中可以看出,由于几何模型以及介质对称的特点,每个源距的感应线圈系所测得的视电导率值均关于x=0的轴线对称.三层对称地层模型下,源距0.3 m和源距0.6 m的线圈系随着仪器向地层中心的移动其视电导率值下降,源距0.9 m和源距1.2 m的线圈系则随着仪器向地层中心的移动其视电导率值先上升后下降(上下围岩共同作用的结果),并且在目的层中心时各源距的线圈系所测到的视电导率值相差最小.仪器位置的变化会影响到每个源距的线圈系所测得的视电导率值且影响规律不同,但仪器越是接近目的层的中心其探测到的电导率也就越接近于目的层的真电导率值,因为此时探测到的目的层信息最丰富,这也是符合基本规律的.
 | 图 2 视电导率随仪器位置变化曲线 Fig. 2 Apparent conductivity changeing with the instrument position curve |
 | 图 3 视电导率随围岩电导率变化曲线 Fig. 3 Apparent conductivity changing with the conductivity of surrounding rock curve |
三层对称地层模型中,上围岩和下围岩对感应测井的影响都是存在的.在不考虑仪器偏心和泥浆侵入的情况下,令仪器距上下围岩距离相等,目的层电导率σt=1 S/m,泥浆电导率σm=2 S/m,计算目的层厚度为2 m时,视电导率值随上下围岩电导率的变化.上下围岩电导率分别为1 S/m、5 S/m、10 S/m、15 S/m、20 S/m、25 S/m和30 S/m.下面来分析仪器水平放置于水平井中时上下围岩电导率的变化对感应测井视电导率值的影响.
在三层对称地层模型中,随源距的增大探测深度是逐渐加深的,由于地层电导率(1 S/m)小于围岩的电导率(大于5 S/m),因而在目的层较薄时,围岩电导率对源距为0.9 m和1.2 m的线圈系的视电导率贡献较大,受趋肤效应影响,在围岩电导率增大的过程中,目的层中的电导率贡献就越来越大,因而这两个线圈系上的视电导率会先增大后减小;相反地,目的层电导率对源距为0.3 m和0.6 m的这两个线圈系的贡献较大,在目的层电导率不变的情况下,围岩电导率的增大会导致这两个线圈系的视电导率值逐渐增大,但围岩电导率增大到某一固定值时,对视电导率的影响将趋于不变.
3.3 目的层厚度的影响同前面的几何模型一样,井径采用8 in(0.2032 m),同时固定目的层电导率σt=1 S/m,上下围岩的电导率σs=10 S/m,泥浆电导率为σm=2 S/m,取层厚从 0.6 m 以步长 0.2 m 增加到 2 m.
图 4是视电导率随目的层厚度变化曲线图.可以看出随着层厚变厚线圈系受围岩的影响也就逐渐变小,所有线圈系的视电导率曲线都是随着层厚增大而变得越来越缓;与此同时,视电阻率值都是随着层厚的增加而逐渐减小,最终趋于变成水平的.因此,各源距测得的目的层电导率对应不同的目的层厚度的校正量是不同的,目的层厚度越小需要校正的量就越大.
 | 图 4 视电导率随目的层厚度变化曲线 Fig. 4 Apparent conductivity changing with the layer thickness curve |
建立的模型为不考虑泥浆侵入的情况,仪器位于井眼中,并且是偏心的,井径为8 in(0.2032 m),井眼位于目的层中,分别取目的层电导率σt=1 S/m,上下围岩的电导率σs=10 S/m,泥浆电导率σm=2 S/m.仪器在井眼中是可以上下运动的,取仪器偏离井眼轴心的距离分别为0 m、0.02 m、0.04 m,0.06 m和0.08 m来分析仪器偏心对视电导率的影响.
图 5是目的层厚为2 m时不同源距下视电导率随仪器偏心距变化的曲线图.可以看出,源距0.3 m的线圈系得到的视电导率值会随着偏心距离的增大有较为明显的减小,并且在偏心距为0.04~0.06 m区间内下降速率最快;其它源距的视电导率值几乎不随偏心距离变化.源距0.3 m的线圈系探测深度较浅,在仪器逐渐偏离井眼的轴心时,源距0.3 m的线圈系探测到地层的信息也会逐渐增多,井眼泥浆电导率(2 S/m)比地层电导率(1 S/m)大,因而源距0.3 m的线圈系所测得的视电导率数值上会逐渐减小.图 6是目的层厚为2 m时不同偏心距下视电导率随源距变化的曲线图.分析图 6可以很清楚地发现只有当源距很小时才需要根据仪器的偏心距对测得的视电导率进行不同程度的校正.
 | 图 5 视电导率随仪器偏心距变化曲线 Fig. 5 Apparent conductivity changing with the instrument eccentricity curve |
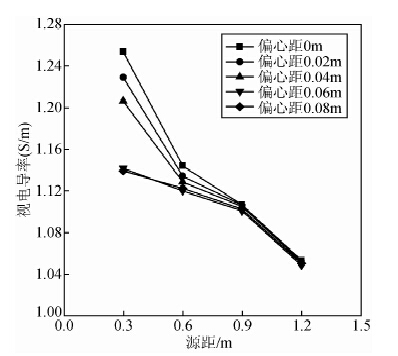 | 图 6 不同偏心距离下视电导率随源距变化曲线 Fig. 6 Apparent conductivity under different eccentric distance changing with spacing curve |
针对水平井感应测井中常见的地层模型(三层对称地层模型),通过正演模拟,分析了仪器位置、上下围岩电导率、目的层厚度和仪器偏心对水平井感应测井响应的影响,对于不同情况下的地层电导率的校正以及前期感应测井仪器设计参数的选择具有指导意义,得到如下结论:
(1)仪器位置的变化会影响到每个源距的线圈系所测得的视电导率值且影响规律不同,但仪器越是接近目的层的中心其探测到的电导率也就越接近于目的层的真电导率值;
(2)受趋肤效应影响,上下围岩电导率的增大会使源距较小的线圈系测得的视电导率逐渐增大,而源距较大的线圈系测得的电导率先增大后减小;
(3)目的层越薄,视电导率值受围岩影响越大,当目的层厚度增大到某一位置时视电导率值将趋于平缓;
(4)源距很小的线圈系会受到仪器偏心的影响,源距较大的线圈系测得的电导率值基本不受仪器偏心的影响.
致 谢 感谢十二五重大专项煤与煤层气地质条件精细探测技术与装备(2011ZX05040-002)的资助;感谢在项目研究期间给予帮助的各位专家老师以及地球物理学进展编辑部的支持与帮助!| [1] | Davydycheva S, Druskin V, Habashy T. 2003. An efficient finite-difference scheme for electromagnetic logging in 3D anisotropic inhomogeneous media[J]. Geophysics, 68(5): 1525-1535. |
| [2] | Hu S, Zhou C C, Wang C X, et al. 2014. Dual induction logging numerical simulation of anisotropic formation in horizontal wells[J]. Science Technology and Engineering (in Chinese), 14(11): 10-13, 26. |
| [3] | Li Z B. 2006. Drilling Geophysical Prospecting (in Chinese)[M]. Beijing: Geological Publishing Press. |
| [4] | Ma H B. 2011. A study on numerical modeling of logging response of trim (in Chinese)[D]. Xi'an: Xi'an Shiyou University. |
| [5] | Pan K J, Wang W J, Tang J T, et al. 2013. Mathematical model and fast finite element modeling of high resolution array lateral logging[J]. Chinese J. Geophys. (in Chinese), 56(9): 3197-3211. |
| [6] | Wang G L, Zhang G J, Cui F X, et al. 2003. Application of staggered grid finite difference method to the computation of 3-D induction logging response[J]. Chinese J. Geophys.(in Chinese), 46(4): 561-567. |
| [7] | Wang H N, Hu P, Tao H G, et al. 2012. Fast algorithm of responses of array multicomponent induction logging tool in horizontally stratified inhomogeneous TI media[J]. Chinese J. Geophys. (in Chinese), 55(2): 717-726, doi: 10.6038/j.issn.0001-5733.2012.02.036. |
| [8] | Wang T, Fang Sheng. 2001. 3-D electromagnetic anisotropy modeling using finite differences[J]. Geophysics, 66(5): 1386-1398. |
| [9] | Wu J, Xie W W, Xie Q C, et al. 2008. Forward response analysis of array lateral logging tool[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 23(1): 73-76. |
| [10] | Wu J, Xu L. 2013. The response characteristics of the horizontal coil of the three components induction logging in thin layers[J]. Progress in Geophysics (in Chinese), 28(4): 1935-1942, doi: 10.6038/pg20130436. |
| [11] | Zhang Y, Wang H N, Tao H G, et al. 2012. Finite volume algorithm to simulate 3D responses of multi-component induction tools in inhomogeneous anisotropic formation based on coupled scalar-vector potentials[J]. Chinese J. Geophys. (in Chinese), 55(6): 2141-2152, doi: 10.6038/j.issn.0001-5733.2012.03.036. |
| [12] | Zhou X G. 2012. Numerical simulation of responses of array induction logging in horizontal wells based on the FEM (in Chinese)[D]. Xi'an: Xi'an Shiyou University. |
| [13] | 胡松, 周灿灿, 王昌学,等. 2014. 水平井各向异性地层双感应测井响应数值模拟[J]. 科学技术与工程, 14(11): 10-13, 26. |
| [14] | 李舟波. 2006. 钻井地球物理勘探[M]. 北京: 地质出版社. |
| [15] | 马欢波. 2011. 随钻感应测井响应数值计算研究[D]. 西安: 西安石油大学. |
| [16] | 潘克家, 王文娟, 汤井田,等. 2013. 高分辨率阵列侧向测井的数学模型及有限元快速正演[J]. 地球物理学报, 56(9): 3197-3211. |
| [17] | 汪功礼, 张庚骥, 崔锋修,等. 2003. 三维感应测井响应计算的交错网格有限差分法[J]. 地球物理学报, 46(4): 561-567. |
| [18] | 汪宏年, 胡平, 陶宏根,等. 2012. 水平层状非均质横向同性地层中阵列多分量感应测井响应的快速计算[J]. 地球物理学报, 55(2): 717-726, doi: 10.6038/j.issn.0001-5733.2012.02.036. |
| [19] | 仵杰, 谢尉尉, 解茜草,等. 2008. 阵列侧向测井仪器的正演响应分析[J]. 西安石油大学学报 (自然科学版), 23(1): 73-76. |
| [20] | 仵杰, 许亮. 2013. 三分量感应水平线圈系在薄层中的响应特性研究[J]. 地球物理学进展, 28(4): 1935-1942, doi: 10.6038/pg20130436. |
| [21] | 张烨, 汪宏年, 陶宏根,等. 2012. 基于耦合标势与矢势的有限体积法模拟非均匀各向异性地层中多分量感应测井三维响应[J]. 地球物理学报, 55(6): 2141-2152, doi: 10.6038/j.issn.0001-5733.2012.03.036. |
| [22] | 周新刚. 2012. 基于有限元法的水平井感应测井响应数值计算研究[D]. 西安: 西安石油大学. |
 2015, Vol. 30
2015, Vol. 30


