波动方程法是应对日益复杂的地质构造地震波传播数值模拟的最重要方法.使用波动方程法进行地震波正演数值模拟时,一般都需要增加人工边界,将无限区域截断成有限区域.为了避免地震波传播到人工边界引起的虚假反射,就需要设置吸收边界条件,使得地震波可以无反射的穿过人工边界.因此,发展形成有效而稳定的吸收边界条件一直是地震波数值模拟的一项重要研究内容.在完全匹配层边界条件出现之前,使用最多的吸收边界条件是基于傍轴近似的单程波动方程吸收条件(Clayton and Engquist,1977;Engquist and Majda,1977).Reynolds也研究提出了类似的吸收边界条件(Reynolds,1978).该边界条件对于小入射角的波具有较好的吸收效果,并且程序实现简单,因此在地震波数值模拟中具有广泛的应用(薛东川等,2007;廉西猛和张睿璇,2013).但是该边界条件在处理高角度入射波时效果较差.另一种吸收边界条件称为海绵吸收方法(Cerjan et al.,1985;Sochacki et al.,1987),即在边界处附加一个空间滤波器或者阻尼椎体,但是该方法要求内部区域到外边界的过渡区要足够大而且光滑,计算量较大,因此未能得到广泛的应用.
直到1994年,Bérenger在研究Maxwell方程时提出了一种新的吸收边界条件——完全匹配层(Perfectly Matched Layer,PML)(renger ,1994),本文称之为经典PML边界条件.该方法在模拟区域外人工增加了一层吸收介质,当波传播到该介质中时,波的能量就被介质吸收,并呈指数级衰减,直至消失,而不会反弹回模拟区域.Bérenger证明,通过合理的设置该层吸收介质,可以使得任何频率的波以任何角度从模拟区域进入吸收介质层时,不产生任何反射,完全匹配层因此而得名.与传统的吸收边界条件相比,完全匹配层具有更优秀的吸收效果(王永刚等,2007;单启铜和乐友喜,2007;李宁等,2011),因此受到了广泛的关注和应用.随着对PML边界条件的研究和应用的不断深入,一些新的PML方法相继被提出,如复频移(Complex Frequency Shifted)卷积PML(Convolutional-PML,C-PML),递归积分PML(Recursive Integral PML,RI-PML),辅助微分方程PML(Auxiliary Differential Equation PML,ADE-PML),近似PML(Nearly PML,N-PML)等方法.这些方法从多个方面完善了经典PML方法,并迅速应用到电磁波,地震波等波传播数值模拟问题中.PML边界条件在20年的发展中,特别是在地震波正演领域的应用中,积累了数量巨大且种类繁多的研究成果,需要进行全面的概括和梳理,但目前尚未有相关的综述性文献发表.
PML边界条件的核心思想是在PML区域内构建一个新的微分方程,使得入射波能够无反射的进入PML区域,并且在PML区域中呈指数级衰减.因此如何构建和求解PML区域内的微分方程是近年来研究的重点问题.为了明确各种PML方法的优缺点和适用范围,使其更好地应用于地震波正演数值模拟中,本文将梳理近年来PML边界条件在地震正演数值模拟领域的研究和应用情况,并进一步讨论PML边界条件研究的趋势和方向.在下一节中,基于二维弹性波方程正演数值模拟方法,作者分层次的阐述了几种PML方法.在最后一节中分析了各种PML方法的异同之处,并在此基础上对PML在地震波正演领域的发展趋势和方向进行了展望.
为了简化讨论,文中涉及的公式推导仅考虑如下的二维弹性波方程:



 表示Χ的Fourier正变换.
1 复坐标伸展PML方法
表示Χ的Fourier正变换.
1 复坐标伸展PML方法
Bérenger于1994年最早提出了PML边界条件的构造方法,其方法的关键是将波场分裂成垂直和平行于PML边界的两部分,进而通过在分裂向量满足的微分方程中增加阻尼项,得到了PML中的微分方程形式.renger(1994)证明如果不进行离散化,该PML边界条件可以完全无反射地吸收所有入射角和所有频率的入射波.该边界条件随后被推广到三维电磁波模拟中(Katz et al.,1994;renger,1996),并被应用到弹性波介质波传播模拟中(Chew and Liu,1996;Hastings et al.,1996).国内的研究成果中,王永刚等人(2007)研究推导了二维声波方程PML边界条件,并针对地面地震模型和井间地震模型(包括均匀介质、层状介质、起伏地表以及由薄层、楔形体和断层组成的复杂模型),将其与旁轴近似吸收边界条件进行了比较,证明了PML边界条件的优越性.单启和乐友喜(2007)研究了二维粘弹性介质的PML边界条件及相应的伪谱法计算公式,并通过对均匀介质模型的模拟,同样验证了PML边界条件具有优于旁轴近似边界条件的吸收效果.严红勇和刘洋(2012)推导了二维黏弹TTI介质PML边界条件满足的微分方程,并给出了相应的基于旋转交错网格的有限差分离散格式.由以上文献可知,经典PML边界条件的优点是吸收效果比传统边界条件更好,缺点是理论尚待完善,实现过程较为复杂.
1.1 复坐标伸展经典PML边界条件的这一缺点很快得到了弥补,Chew和Weedon以及Collino和Monk对Bérenger提出的PML进行了一般性的推导(Chew and Weedon,1994;Collino and Monk,1998),将其解释为复坐标伸展变换(Complex Coordinate Stretching,CCS)的结果.考虑频率域弹性波方程(2),引入复坐标变换为
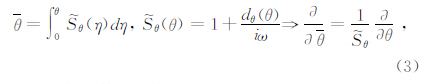

理论上,对于平面波Aexp(-i( k·x -ω t ))(其中A表示振幅,k =(kx,kz)表示波矢量),在PML区域中满足(以x方向为例)

但是该方法存在一些短板.(5)中的波矢量k可表示为kx=cosγ/cp,kz=sinγ/cp,cp表示相速度,则衰减系数D可表示为

为了解决CCS方法存在的问题,Kuzuoglu和Mittra(1996)提出了复频移(Complex Frequency Shifted,CFS)PML边界条件,其思路为对(3)中复坐标伸展变换形式进行如下修正,公式为


虽然CFS-PML边界条件具有诸多优点,但是该方法最初并未获得广泛的认同,原因是基于CFS-PML边界条件形成的微分方程系统不可避免的需要引入更多地辅助变量,求解该系统时需要进行大量卷积计算,代价十分巨大.直到一系列非分裂算法(Gedney,1996;Roden and Gedney,2000)提出之后,CFS-PML才逐渐受到广泛关注和应用.
2 非分裂波场PML方法为了避免卷积计算,经典PML使用了波场分裂的处理方式,因此又称为场分裂PML(Split PML,S-PML).对于S-PML的研究,除了前文提到的一些文献之外,李景叶和陈小宏(2006)研究了SPML在TI介质弹性波方程数值模拟方法的处理方法,并应用交错网格高阶差分技术进行了求解.裴正林(2004)将S-PML推广到三维,并应用于各向异性弹性波波场的模拟,其由于场分裂而引入的辅助变量个数多达54个,占用大量存储空间,并且在在计算区域的6个面、12个棱以及8个角点上的处理方式均不尽相同,编程十分复杂。为此,刘有山等(2012)针对二阶弹性波方程的S-PML分别提出了改进的办法,通过对卷积采用近似计算,避免了计算时间的三阶倒数,减少了辅助变量的个数,降低了存储需求和编程复杂度.尽管如此,S-PML存储需求大的问题仍未得到较好解决.除此之外,S-PML还存在场分裂的方式并不具有实际的物理意义,以及模拟结束后进行波场合并时会引入一些数值误差等缺点.CFS技术的使用放大了S-PML的缺点,激励研究者去寻求新的PML实现方法.
如果不使用场分裂的方式,即直接将(4)式转换到时间域,则可得
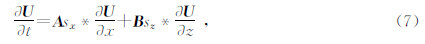
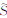 θ的逆Fourier变换.为了提高(7)式的求解效率,必须寻求合适的方法替代或者回避(7)式中的卷积计算.应用较广泛的解决方案包括了递归卷积法,递归积分法以及递归微分法等.
2.1 递归卷积法
θ的逆Fourier变换.为了提高(7)式的求解效率,必须寻求合适的方法替代或者回避(7)式中的卷积计算.应用较广泛的解决方案包括了递归卷积法,递归积分法以及递归微分法等.
2.1 递归卷积法
Roden和Gedney(2000)提出了一种基于CFS的PML边界条件,其推导基于利用递归方法计算卷积的思想(Luebbers and Hunsberger,1992),因此命名为C-PML.由上文中的(6)式可得





求解微分方程和即可完成PML区域中的计算,这种方式大大降低了编程的复杂度.随后,Komatitsch、Martin等人对该方法进行了深入的研究,并将其应用到弹性介质(Komatitsch and Martin,2007)、多孔弹性介质(Martin et al.,2008a)、各向异性介质(Martin et al.,2008b)以及黏弹性介质(Martin and Komatitsch,2009)的地震波传播数值模拟问题中,提高了高角度入射波/掠入波的吸收效果.张鲁新等(2010)将C-PML方法引入到孔隙弹性介质速度-应力格式的旋转交错网格有限差分算法中,并通过数值分析得到了一组优化的吸收边界参数.杜启振等人(2011)推导了二维三分量TTI介质的弹性波的C-PML,进行了由C-PML与自由边界条件构成的组合边界条件下的波场模拟,这种方式比全部边界都应用C-PML的情形更接近物理实际.
2.2 递归积分法
递归积分PML最早由Drossaert和Giannopoulos(2007)提出,被称为RI-PML.该方法通过引入辅助变量巧妙的回避了卷积运算,代之以时间积分方程的近似求解.Drossaert的推导基于复伸展坐标变换CCS,对于(4)式,引入辅助变量 Q (其Fourier变换定义为  θ)满足
θ)满足



张显文等(2009)(张显文和韩立国,2008)推广了Drossaert和Giannopoulos(2007)的推导,将复频移技术引入RI-PML方法中,并应用到二维和三维弹性波方程交错网格高阶差分方法数值模拟中.注意到,RI-PML方法与C-PML方法的吸收效果相差无几,但是求解过程要复杂很多,因此未得到广泛的研究和应用.
2.3 递归微分法
等(2009b)使用了一种新型的辅助变量定义方法,推导出该辅助变量满足的微分方程,进而通过递归求解微分方程的方法求得辅助变量,本文称之为递归微分法. 等(2009)首先基于复坐标变换推导了该方法,随后 (Qin et al.,2009)将复频移技术引入该PML的实现中.与C-PML不同, 等人在频率域引入辅助变量 θ满足条件为
θ满足条件为

对于微分方程(16), 等人(Qin et al.,2009)给出了一种递归的求解方法,同样得到了递归求解公式(11)~(12).通过与其他PML比较可以发现,各种PML的吸收效果十分接近,但是该方法编程实现更为简单,内存使用更少,更适合应用到三维问题.熊章强和毛承英(2011)应用该边界条件研究了一阶压力-速度偏微分形式的声波方程.
三种方法的区别主要在于引入辅助变量的方式,递归卷积方法在时间域引入辅助变量,而其他两种方法都在频率域引入辅助变量,进而转换到时间域中得到关于辅助变量的微分或积分方程形式,避开了卷积计算.事实上,(16)式中的辅助变量  θ是C-PML中(9)式引入的辅助变量 Q θ的Fourier正变换形式,因而最终得到的辅助变量的递归求解公式也是相同的.
θ是C-PML中(9)式引入的辅助变量 Q θ的Fourier正变换形式,因而最终得到的辅助变量的递归求解公式也是相同的.
PML边界条件从分裂波场方式到非分裂波场方式是一次巨大的进步.首先,非分裂波场PML避免了非物理的波场分裂引起的数值误差;其次,非分裂波场PML简单而高效的引入了复频移技术,提高了高角度入射波和瞬逝波的吸收效果.至此,PML边界条件的吸收效果已经可以满足实际生产应用的需要.
3 新型PML方法微分方程显式数值离散格式一般都受到CFL(Courant-Friedrichs-Lewy)稳定性条件的限制,模拟的精度不仅取决于空间离散格式的精度,还与时间离散的逼近精度有关,因此许多高阶时间离散格式( Käser and Dumbser,2006;李博和李敏,2011)开始被引进到地震波正演数值模拟领域中.C-PML和RI-PML所采用的递归方式限制了时间的离散方式,时间逼近精度较低,且难以应用到更高阶的时间离散格式中.因此,适用于高阶时间离散格式的新型PML边界条件也逐渐发展起来.
3.1 辅助微分方程PML辅助微分方程PML边界条件最初由Ramadan(2003)首先使用. 等(2009;Qin et al.,2009)和熊章强和毛承英(2011)推导出了ADE-PML满足的方程(16),然后使用了二阶精度的递归离散格式进行求解,因此可以把递归微分法PML视为ADE-PML的一种特殊情形.Gedney和Zhao(2010)拓展了上文中的递归方法,将上述辅助变量的递归格式改写成微分方程形式,并解释为辅助变量的时间演化微分方程,然后利用高阶的时间离散格式求解此微分方程.Martin等(2010)系统的推导了ADE-PML,得到了微分方程系统(10)和(16),并应用四阶Runge-Kutta方法进行时间离散.该方法优化了对高角度入射波/掠入波的吸收效果,长时间计算稳定性可达100,000个时间步,并且获得比C-PML更高的模拟精度.Zhang和Shen(2010)利用ADE-PML研究三维弹性波方程地震波数值模拟问题,选用了二阶蛙跳格式和四阶Runge-Kutta两种时间离散格式.同时,他们还理论分析了尺度因子β的作用,并给出了其最优取值.赵建国等(2014)将ADE-PML应用到一阶压力-速度形式的声波方程数值模拟中,采用四阶Runge-Kutta时间格式,并研究了采用显式,隐式和半隐式格式时吸收效果存在的差异,指出显式格式时效果最好.
3.2 近似PML近似PML最早由Cummer(2003)提出,并应用于二维弹性电磁场模拟问题中,其核心思想为将对坐标的伸展变换转化为对波场的伸展变换.Cummer的推导基于复伸展坐标变换(3),在频率域引入变换公式为


注意到(18)式与内部区域满足的弹性波方程(1)具有相同的形式,因此编程实现时,内部区域的程序代码可以重用在PML区域上,PML区域中只需额外求解常微分方程(17)即可.Cummer指出如果dθ依赖于θ,则上述推导在数学上是不严格正确的,因此Cummer将此方法称之为近似(Nearly)PML方法.但是Hu和Cummer(2004)随后从理论分析和数值实验上证明了在笛卡尔坐标系中N-PML方法等价于标准的PML方法,但是在后续的研究文献中N-PML的名称仍被沿用.由于N-PML理论简洁、易于实现,因此迅速得到了研究和应用.Hu等(2007)将N-PML边界条件应用到声波方程数值模拟问题中.Chen et al.将N-PML推广到各向同性均匀(Chen,2011)、各向异性弹性(Chen and Zhao,2011)以及多孔弹性(Chen,2012)等介质中地震波传播数值模拟中.McGarry和Moghaddam(2009)推导了二阶声波方程的N-PML边界条件,拓展了N-PML的应用范围.Metin等(2013)将此成果应用到声波叠前逆时偏移算法的波场正演模拟部分中,取得不错的吸收效果和计算效率.
相比于基于递归方法的PML,ADE-PML和N-PML中推导出了辅助变量满足的微分方程形式,进而可以使用逼近精度更高的(多步法或单步法)时间离散格式求解辅助变量,从而提高了正演模拟精度.
4 总结与展望
综上所述,PML边界条件经历了从特例到一般化的发展过程:特殊情形下的解决方案首先被提出,然后为了解决该方案存在的问题,特例方案被改进提升,最后得到一般化解决方案.我们归纳了几种PML边界条件之间的一致性或者包含关系,使用数学符号  表示一般化形式和特例之间的包含关系,
表示一般化形式和特例之间的包含关系, 表示相似关系.
表示相似关系.
(1)CFS  CCS
CCS
注意到,若在式(6)中取β=1,α=0,则得到(3)式,可见复坐标伸展变换是复频移变换的一种特殊形式.两者在吸收效果上也具有包含性.基于复坐标伸展变换的PML只对小角度、频率较高的入射波具有良好的吸收效果,基于复频移变换的PML则可以吸收各种角度、各种频率的入射波.
(2)ADE-PML C-PML≌ 递归微分法
C-PML≌ 递归微分法
张鲁新等(2010)推导了C-PML与递归微分法的等价关系,Martin等(2010)证明了ADE-PML与C-PML的包含关系,递归微分法的推导过程(等,2009;Qin et al.,2009;熊章强和毛承英,2011)也隐含了这一关系
(3)N-PML≌ ADE-PML
事实上,在(16)中引入变换  θ=
θ=  θ(t)
θ(t)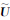 ,则 Q θ=
,则 Q θ=  P θ/
P θ/ θ,代入ADE-PML的微分方程(10)和(16),即可得到基于复频移伸展变换的N-PML边界条件(薛昭等,2014).注意到,基于复频移伸展变换的N-PML边界条件中PML区域的微分方程已经不完全与内部区域相同,而是多了若干项,其编程复杂度也与ADE-PML相当.
θ,代入ADE-PML的微分方程(10)和(16),即可得到基于复频移伸展变换的N-PML边界条件(薛昭等,2014).注意到,基于复频移伸展变换的N-PML边界条件中PML区域的微分方程已经不完全与内部区域相同,而是多了若干项,其编程复杂度也与ADE-PML相当.
另一方面,从经典的PML到CPML,再到ADE-PML,边界的吸收效果和正演模拟精度是在不断提升的.数值试验可以证实这一点.我们使用了D. Komatitsch和R. Martin开发的地震正演模拟开源程序包SEISMIC_CPML,选取了程序包中的三个二维各向同性弹性波正演程序,分别使用经典PML、C-PML和ADE-PML边界条件进行对比试验.三个程序均使用了大小为101×641的单层介质速度模型,纵横波速度分别为3300和1905米/秒,PML边界宽度为10个网格点间隔,炮点和接收点位置相同,震源采用了Gaussian点震源,主频为7Hz.经典PML和C-PML程序都采用了交错网格二阶空间离散和二阶时间离散的有限差分方法,而ADE-PML程序由于可以使用高阶时间离散格式,因此采用了交错网格八阶空间离散格式和四阶Runge-Kutta时间离散方法.
图 1中(a)-(d)分别为600,900,1200和1300毫秒时刻的波场快照,黄色十字代表震源,绿色代表接收点.比较经典PML和C-PML边界条件可以发现,由于没有使用复频移技术,经典PML边界条件在右侧边界处仍有高角度入射波未有效吸收,引起了虚假的波场出现.而使用了复频移技术的C-PML边界条件具有更好的边界吸收效果.ADE-PML边界条件由于使用了更高阶的空间和时间离散精度,因此其模拟精度比C-PML更优越,在(a)-(c)的时刻时,ADE-PML与C-PML的模拟效果相差不大,而当能量较大的纵波传播出区域时,可以发现C-PML(见图 1中C-PML-(d))未能在两侧边界有效吸收低频的横波,而ADE-PML(见图 1中ADE-PML-(d))则很好的做到了这一点.
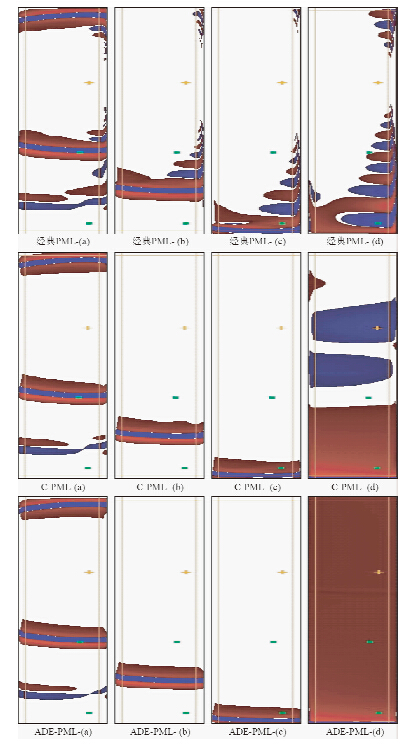 |
图 1 各种PML边界条件吸收效果比较 Fig. 1 Comparison among three kinds of PMLs |
PML边界条件作为地震波正演模拟的重要组成部分,是与正演模拟算法相辅相成,共同发展的.事实上,从发展历程来看,每当正演模拟领域有新方法或新技术提出,就会出现于之相匹配的PML边界条件;反之,每当一种新的PML边界条件被提出,其很快就会被应用到各种正演算法中去.
地震波正演数值模拟使用的数值方法主要是时域有限差分(Finite Difference Time Domain,FDTD)方法,基于该方法的PML边界条件的研究已经十分全面和成熟,PML边界条件已经成功应用与基于交错网格(裴正林,2004),旋转交错网格(陈浩等,2006)等技术的FDTD方法中,由于使用了CFS变换,正演算法对于低频和高角度入射波的吸收效果也较为理想.随着地震正演模拟技术的迅速发展,为了提高模拟的精度和效率,许多先进的方法被提出或引入到该领域,例如高阶时间方法(李博和李敏,2011)、变网格大小变时间步长技术(孙林洁和印兴耀,2011)、新型微分方程数值解法(Käser and Cumbser,2006;Etienne et al.,2010)、非正交网格剖分技术(廉西猛和张睿璇,2013;薛昭等,2014)以及多核异构平台并行加速技术(Toivanen et al.,2011).这些方法,逐渐成为地震正演模拟研究的热点,而与这些方法相匹配的PML边界条件的研究也将成为热点.
本文将以上热点作为衡量标准对比了前文中提到几种PML边界条件(表 1).可以发现:
|
|
表 1 几种PML边界条件比较 Table 1 Comparison of some PMLs |
(1)S-PML的主要劣势在于使用了场分裂,场分裂需要引入许多辅助变量,特别是处理三维问题时,大量的辅助变量(Marcinkovich and Olsen,2003)占用了过多的内存存储,严重影响计算效率.在此基础上引入复频移技术会进一步增加辅助变量的数量,巨大的存储需求和复杂的程序实现使得该边界条件失去了实际应用价值.
尽管如此,作为最基础PML边界条件,由于其限制条件最少,所以经常被用作新型正演模拟技术与PML的适应性研究,如有限元方法(刘有山等,2004)、有限体积(格子)方法(徐义和张剑锋,2008)、可变网格技术(孙林洁和印兴耀,2011)以及基于三角网格的谱元法(刘有山等,2014)等.因此,S-PML边界条件在未来的研究中仍能发挥重要作用.
(2)由于目前的大规模三维正演模拟算法仍基于有限差分方法,因此C-PML仍然是目前应用最多的吸收边界条件.随着高性能计算技术在正演模拟领域的应用,C-PML边界条件在多核异构等平台上的并行策略也逐渐成为研究的热点(Toivanen et al.,2011).但是由于C-PML推导使用了递归方法,因此C-PML(以及RI-PML)存在诸多限制,如无法使用高阶的时间离散格式,难以适应空间网格的灵活变化等,这些都将影响其对于新型正演模拟技术的适应性.
(3)对于ADE-PML和N-PML,其辅助变量和原有变量都是基于微分方程求解,理论上能应用在原有变量微分方程上的技术或方法,都可以应用到辅助变量的微分方程上,因此这两种方法在各方面都具有良好的适应性.目前,基于ADE-PML边界条件的正演算法可以使用四阶Runge-Kutta等高阶时间离散格式(Martin et al.,2010;Zhang and Shen,2010),而在基于间断有限元方法等非有限差分方法的正演模拟方法(Etienne et al.,2010;薛昭等,2014)中和基于多核异构平台的逆时偏移算法(刘守伟等,2013)中都使用了N-PML边界条件.所以,这两种PML边界条件将具有更广阔的研究和应用前景.
致 谢 感谢审稿专家对本文提出的宝贵意见和建议.
| [1] | Bérenger J -P. 1994. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 114(2):185-200. |
| [2] | Bérenger J -P. 1996. Three-dimensional perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 127(2):363-379. |
| [3] | Bérenger J -P. 2002a. Application of the CFS PML to the absorption of evanescent waves in wave guides[J]. IEEE Microwave and Wireless Components Letters, 12(6):218-220. |
| [4] | Bérenger J -P. 2002b. Numerical reflection from FDTD-PMLs:a comparison of the split PML with the unsplit and CFS PMLs[J]. IEEE Transactions on Antennas and Propagation, 50(3):258-265. |
| [5] | Cerjan C, Kosloff D. Kosloff R, et al. 1985. A nonreflecting boundary condition for discrete acoustic and elastic wave equations[J]. Geophysics, 50(4):705-708. |
| [6] | Chen H, Wang X M, Zhao H B. 2006. A rotated staggered grid finite-differencewith the absorbing boundary condition of a perfectly matched layer[J]. Chinese Science Bulletin, 51(19):2304-2314. |
| [7] | Chen J Y. 2011. Application of the nearly perfectly matched layer for seismic wave propagation in 2D homogeneous isotropic media[J]. Geophysical Prospecting, 59(4):662-672. |
| [8] | Chen J, Zhao J. 2011. Application of the nearly perfectly matched layer to seismic-wave propagation modeling in elastic anisotropic media[J]. Bulletin of the Seismological Society of America, 101(6):2866-2871. |
| [9] | Chen J Y. 2012. Nearly perfectly matched layer method for seismic wave propagation in poroelastic media[J]. Canadian Journal of Exploration Geophysics, 37(1):22-27. |
| [10] | Chew W C, Liu Q H. 1996. Perfectly matched layers for elastodynamics:A new absorbing boundary condition[J]. Journal of Computational Acoustics, 4(4):341-359. |
| [11] | Chew W C, Weedon W H. 1994. A 3D perfectly matched medium from modified maxwell's equations with stretched coordinates[J]. Microwave and Optical Technology Letters, 7(13):599-604. |
| [12] | Clayton R, Engquist B. 1977. Absorbing boundary conditions for acoustic and elastic wave equations[J]. Bull. Seism. Soc. Am., 67(6):1529-1540. |
| [13] | Collino F, Monk P B. 1998. Optimizing the perfectly matched layer[J]. Comput. Meth. Appl. Mech. Eng., 164(1-2):157-171. |
| [14] | Collino F, Tsogka C. 2001. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 66(1):294-307. |
| [15] | Cummer S A. 2003. A simple, nearly perfectly matched layer for general electromagnetic media[J]. IEEE Microwave and Wireless Components Letters, 13(3):128-130. |
| [16] | Drossaert F, Giannopoulos A. 2007. A nonsplit complex frequency-shifted PML based on recursive integration for FDTD modeling of elastic waves[J]. Geophysics, 72(2):9-17. |
| [17] | Du Q Z, Sun R Y, Zhang Q. 2011. Numerical simulation of three-component elastic wavefield in 2D TTI media in the condition of the combined boundary[J]. OGP (in Chinese), 46(2):187-195. |
| [18] | Engquist B, Majda A. 1977. Absorbing boundary conditions for the numerical simulation of waves[J]. Math. Comp., 31(139):629-651. |
| [19] | Gedney S D. 1996. An anisotropic PML absorbing media for the FDTD simulation of fields in lossy and dispersive media[J]. Electromagnetics, 16(4):399-415. |
| [20] | Gedney S D, Zhao B. 2010. An auxiliary differential equation formulation for the complex-frequency shifted PML[J]. IEEE Transactions on Antennas and Propagation, 58(3):838-847. |
| [21] | Hastings F D, Schneider J B, Broschat S L. 1996. Application of the perfectly matched layer (PML) absorbing boundary condition to elastic wave propagation[J]. The Journal of the Acoustical Society of America, 100(5):3061-3069. |
| [22] | Hu W Y, Cummer S A. 2004. The nearly perfectly matched layer is a perfectly matched layer[J]. IEEE Antennas and Wireless propagation Letters, 3(1):137-140. |
| [23] | Hu W Y, Abubakar A, Habashy T M. 2007. Application of the nearly perfectly matched layer in acoustic wave modeling[J]. Geophysics, 72(5):SM169-SM175. |
| [24] | Käser M, Dumbser M. 2006. An arbitrary high order discontinuous Galerkin method for elastic waves on unstructured meshes -I. The two-dimensional isotropic case with external source terms[J]. Geophys. J. Int., 166(2):855-877. |
| [25] | Katz D S, Thiele E T, Taflove A. 1994. Validation and extension to three dimensions of Berenger PML absorbing boundary condition for FD-TD meshes[J]. IEEE Microwave and Guided Wave Letters, 4(8):268-270. |
| [26] | Komatitsch D, Tromp J. 2003. A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation[J]. Geophys. J. Int., 154(1):146-153. |
| [27] | Komatitsch D, Martin R. 2007. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation[J]. Geophysics, 72(5):SM155-SM167. |
| [28] | Kuzuoglu M, Mittra R. 1996. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers[J]. IEEE Microwave and Guided Wave Letters, 6(12):447-449. |
| [29] | Li B, Li M. 2011. High-order finite difference scheme in time for wave field simulation[C].//The 27th Annual Meeting of the Chinese Geophysical Society Proceedings (in Chinese). |
| [30] | Li J Y, Chen X H. 2006. Treatment of the boundary conditions in the numerical simulation of the seismic wave field in transversely isotropic (TI) medium[J]. Journal of Xi'an Shiyou University (Nature Science Edition) (in Chinese), 2006, 21(4):20-23. |
| [31] | Li N, Xie L L, Zhai C H. 2007. Comparison of perfectly matched layer and multi-transmitting formular artificial boundary conditions based on hybrid finite element formulation[J]. Acta Seismologica Sinica (in Chinese), 29(6):643-653. |
| [32] | Lian X M, Zhang R X. 2013. Numerical simulation of seismic wave equation by local discontinuous Galerkin method[J]. Chinese J. Geophys. (in Chinese), 56(10):3507-3513, doi:10.6038/cjg20131025. |
| [33] | Liu S W, Wang H Z, Chen S C, et al. 2013. Implementation strategy of 3D reverse time migration on GPU/CPU cluster[J]. Chinese J. Geophys. (in Chinese), 56(10):3487-3496, doi:10.6038/cjg20131023. |
| [34] | Liu Y S, Liu S L, Zhang M G, et al. 2012. An improved perfectly matched layer absorbing boundary condition for second order elastic wave equation[J]. Progress in Geophysics (in Chinese), 27(5):2113-2122, doi:10.6038/j.issn.1004-2903.2012.05.036. |
| [35] | Liu Y S, Teng J W, Liu S L, et al. 2013. Explicit finite element method with triangle meshes stored by sparse format and its perfectly matched layers absorbing boundary condition[J]. Chinese J. Geophys. (in Chinese), 56(9):3085-3099, doi:10.6038/cjg20130921. |
| [36] | Luebbers R J, Hunsberger F. 1992. FDTD for Nth-Order dispersive media[J]. IEEE Transactions on Antennas and Propagation, 40(11):1297-1301. |
| [37] | Marcinkovich C, Olsen K. 2003. On the implementation of perfectly matched layers in a three-dimensional fourth-order velocity-stress finite difference scheme[J]. J. Geophys. Res., 108(B5):2276, doi:10.1029/2002JB002235. |
| [38] | Martin R, Komatitsch D, Ezziani A. 2008a. An unsplit convolutional perfectly matched layer improved at grazing incidence for seismic wave propagation in poroelastic media[J]. Geophysics, 73(4):T51-T61. |
| [39] | Martin R, Komatitsch D, Gedney S D. 2008b. A variational formulation of a stabilized unsplit convolutional perfectly matched layer for the isotropic or anisotropic seismic wave equation[J]. CMES:Computer Modeling in Engineering & Sciences, 37(3):274-304. |
| [40] | Martin R, Komatitsch D. 2009. An unsplit convolutional perfectly matched layer technique improved at grazing incidence for the viscoelastic wave equation[J]. Geophys. J. Int., 179(1):333-344. |
| [41] | Martin R, Komatitsch D, Gedney S D, et al. 2010. A high-order time and space formulation of the unsplit perfectly matched layer for the seismic wave equation using auxiliary differential equations (ADE-PML)[J]. CMES:Computer Modeling in Engineering and Sciences, 56(1):17-42. |
| [42] | McGarry R, Moghaddam P. 2009. NPML boundary conditions for second-order wave equations[C].//79th Ann. Internat. Mtg., Soc. Expi. Geophys., Expanded Abstracts, 3590-3594. |
| [43] | Metin G, Chen J Y, Ozsoy C. 2013. Application of nearly perfectly matched layer with second-order acoustic equations in seismic numerical modeling[J]. J. Geol. Geosci., 2:120, doi:10.4172/2329-6755.1000120. |
| [44] | Pei Z L. 2004. Three-dimensional numerical simulation of elastic wave propagation in 3-D anisotropic media with staggered-grid high-order difference method[J]. Journal of the University of Petroleum China (in Chinese), 28(5):23-29. |
| [45] | Qin Z, Lu M H, Zheng X D, et al. 2009. The implementation of an improved NPML absorbing boundary condition in elastic wave modeling[J]. Applied Geophysics, 6(2):113-121. |
| [46] | Qin Z, Ren P G, Yao Y, et al. 2009. Improvement of PML absorbing boundary conditions in elastic wave forward modeling[J]. Earth Science-Journal of China University of Geosciences (in Chinese), 34(4):658-664. |
| [47] | Ramadan O. 2003. Auxiliary differential equation formulation:An efficient implementation of the perfectly matched layer[J]. IEEE Microwave and Wireless Components Letters, 13(2):69-71. |
| [48] | Reynolds A C. 1978. Boundary conditions for the numerical solution of wave propagation problems[J]. Geophysics, 43(6):1099-1110. |
| [49] | Roden J A, Gedney S D. 2000. Convolution PML (CPML):An efficient FDTD implementation of the CFS-PML for arbitrary media[J]. Microwave and Optical Technology Letters, 27(5):334-339. |
| [50] | Shan Q T, Le Y X. 2007. Wavefield simulation of 2-D viscoelastic medium in perfectly matched layer boundary[J]. Geophysical Prospecting for Petroleum (in Chinese), 46(2):126-130. |
| [51] | Sochacki J, Kubichek R, George J, et al. 1987. Absorbing boundary conditions and surface waves[J]. Geophysics, 52(1):60-71. |
| [52] | Sun L J, Yin X Y. 2011. A finite-difference scheme based on PML boundary condition with high power grid step variation[J]. Chinese J. Geophys. (in Chinese), 54(6):1614-1623, doi:10.3969/j.issn.0001-5733.2011.06.021. |
| [53] | Toivanen J I, Stefanski T P, Kuster N, et al. 2011. Comparison of CPML implementations for the GPU-accelerated FDTD solver[J]. Progress in Electromagnetics Research M, 19:61-75. |
| [54] | Xiong Z Q, Mao C Y. 2011. Improved unsplit PML boundary conditions in acoustic wave numerical simulation[J]. Oil Geophysical Prospecting (in Chinese), 46(1):35-39. |
| [55] | Xu Y, Zhang J F. 2008. An Irregular-grid perfectly matched layer absorbing boundary for seismic wave modeling[J]. Chinese J. Geophys. (in Chinese), 51(5):1520-1526. |
| [56] | Xue D C, Wang S X, Jiao S J. 2007. Wave equation finite-element modeling including rugged topography and complicated medium[J]. Progress in Geophysics (in Chinese), 22(2):522-529. |
| [57] | Xue Z, Dong L G, Li X B, et al. 2014. Discontinuous Galerkin finite-element method for elastic wave modeling including surface topography[J]. Chinese J. Geophys. (in Chinese), 57(4):1209-1223, doi:10.6038/cjg20140418. |
| [58] | Yan H Y, Liu Y. 2012. Rotated staggered grid high-order finite-difference numerical modeling for wave propagation in viscoelastic TTI media[J]. Chinese J. Geophys. (in Chinese), 55(4):1354-1365, doi:10.6038/j.issn.0001-5733.2012.04.031. |
| [59] | Zhang L X, Fu L Y, Pei Z L. 2012. Finite difference modeling of Biot's poroelastic equations with unsplit convolutional PML and rotated staggered grid[J]. Chinese J. Geophys. (in Chinese), 53(10):2470-2483, doi:10.3969/j.issn.0001-5733.2010.10.021. |
| [60] | Zhang W, Shen Y. 2010. Unsplit complex frequency-shifted PML implementation using auxiliary differential equations for seismic wave modeling[J]. Geophysics, 75(4):T141-T54. |
| [61] | Zhang X W, Han L G. 2008. A complex frequency-shifted PML based on recursive integration for modeling of 3D elastic wave equation[C].//The 24th Annual Meeting of the Chinese Geophysical Society Proceedings(in Chinese). |
| [62] | Zhang X W, Han L G, Huang L, et al. 2009. A staggered-grid high-order difference method of complex frequency-shifted PML based on recursive integration for elastic wave equation[J]. Chinese J. Geophys. (in Chinese), 52(7):1800-1807, doi:10.3969/j.issn.0001-5733.2009.07.014. |
| [63] | Zhao H B, Wang X M, Wang D, et al. 2007. Applications of the boundary absorption using a perfectly matched layer for elastic wave simulation in poroelastic media[J]. Chinese J. Geophys. (in Chinese), 50(2):581-591. |
| [64] | Zhao J G, Shi R Q. 2013. Perfectly matched layer-absorbing boundary condition for finite-element time-domain modeling of elastic wave equations[J]. Applied Geophysics, 10(3):323-336. |
| [65] | Zhao J G, Shi R Q, Chen J Y, et al. 2014. Application of auxiliary differential equation perfectly matched layer for numerical modeling of acoustic wave equations[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 44(2):675-682. |
| [66] | Zeng Y Q, He J Q, Liu Q H. 2001. The application of the perfectly matched layer in numerical modeling of wave propagation in poroelastic media[J]. Geophysics, 66(4):1258-1266. |
| [67] | 陈浩,王秀明,赵海波. 2006.旋转交错网格有限差分及其完全匹配层吸收边界条件[J].科学通报, 51(17):1985-1994. |
| [68] | 杜启振,孙瑞艳,张强. 2011.组合边界条件下二维三分量TTI介质波场数值模拟[J].石油地球物理勘探, 46(2):187-195. |
| [69] | 李博,李敏. 2011.时间高阶显式有限差分波场模拟[C].//中国地球物理学会第二十七届年会论文集. |
| [70] | 李景叶,陈小宏. 2006. TI介质地震波场数值模拟边界条件处理[J].西安石油大学学报(自然科学版), 21(4):20-23. |
| [71] | 李宁,谢礼立,翟长海. 2011.基于混合有限元格式的完美匹配层与多次透射公式人工边界比较研究[J].地震学报, 29(6):643-653. |
| [72] | 廉西猛,张睿璇. 2013.地震波动方程的局部间断有限元方法数值模拟[J].地球物理学报, 56(10):3507-3513, doi:10.6038/cjg20131025. |
| [73] | 刘守伟,王华忠,陈生昌,等. 2013.三维逆时偏移GPU/CPU机群实现方案研究[J].地球物理学报, 56(10):3487-3496, doi:10.6038/cjg20131023. |
| [74] | 刘有山,刘少林,张美根,等. 2012.一种改进的二阶弹性波动方程的最佳匹配层吸收边界条件[J].地球物理学进展, 27(5):2113-2122, doi:10.6038/j.issn.1004-2903.2012.05.036. |
| [75] | 刘有山,滕吉文,刘少林,等. 2013.稀疏存储的显式有限元三角网格地震波数值模拟及其PML吸收边界条件[J].地球物理学报, 56(9):3085-3099, doi:10.6038/cjg20130921. |
| [76] | 裴正林. 2004.三维各向异性介质中弹性波方程交错网格高阶有限差分法数值模拟[J].石油大学学报, 28(5):23-29. |
| [77] | ,任培罡,姚姚,等. 2009.弹性波正演模拟中PML吸收边界条件的改进[J].地球科学-中国地质大学学报, 34(4):658-664. |
| [78] | 单启铜,乐友喜. 2007. PML边界条件下二维粘弹性介质波场模拟[J].石油物探, 46(2):126-130. |
| [79] | 孙林洁,印兴耀. 2011.基于PML边界条件的高倍可变网格有限差分数值模拟方法[J].地球物理学报, 54(6):1614-1623, doi:10.3969/j.issn.0001-5733.2011.06.021. |
| [80] | 熊章强,毛承英. 2011.声波数值模拟中改进的非分裂式PML边界条件[J].石油地球物理勘探, 46(1):35-39. |
| [81] | 徐义,张剑锋. 2008.地震波数值模拟的非规则网格PML吸收边界[J].地球物理学报, 51(5):1520-1526. |
| [82] | 薛东川,王尚旭,焦淑静. 2007.起伏地表复杂介质波动方程有限元数值模拟方法[J].地球物理学进展, 22(2):522-529. |
| [83] | 薛昭,董良国,李晓波,等. 2014.起伏地表弹性波传播的间断Galerkin有限元数值模拟方法[J].地球物理学报, 57(4):1209-1223, doi:10.6038/cjg20140418. |
| [84] | 严红勇,刘洋. 2012.黏弹TTI介质中旋转交错网格高阶有限差分数值模拟[J].地球物理学报, 55(4):1354-1365, doi:10.6038/j.issn.0001-5733.2012.04.031. |
| [85] | 张鲁新,符力耘,裴正林. 2010.不分裂卷积完全匹配层与旋转交错网格有限差分在孔隙弹性介质模拟中的应用[J].地球物理学报, 53(10):2470-2483, doi:10.3969/j.issn.0001-5733.2010.10.021. |
| [86] | 张显文,韩立国. 2008.基于递归积分的复频移PML三维弹性波模拟[C].//中国地球物理学会第二十四届年会论文集. |
| [87] | 张显文,韩立国,黄玲,等. 2009.基于递归积分的复频移PML弹性波方程交错网格高阶差分法[J].地球物理学报, 52(7):1800-1807, doi:10.3969/j.issn.0001-5733.2009.07.014. |
| [88] | 赵海波,王秀明,王东,等. 2007.完全匹配层吸收边界在孔隙介质弹性波模拟中的应用[J].地球物理学报, 50(2):581-591. |
| [89] | 赵建国,史瑞其,陈竞一,等. 2014.辅助微分方程完全匹配层在声波方程数值模拟中的应用[J].吉林大学学报(地球科学版), 44(2):675-682. |
 2015, Vol. 30
2015, Vol. 30

