叠前逆时偏移(RTM)是一种高精度的地震成像技术,不仅可以突破地层倾角的限制,也可对回转波、棱柱波和多次反射波等多种波进行成像.早在20世纪80年代,RTM方法由许多学者提出(Whitmore,1983;Baysal et al.,1983;McMechan,1983;Loewenthal et al.,1987),但是由于RTM方法对硬件的要求较高,一直发展缓慢.近年来,随着计算机硬件技术的发展,逆时偏移方法越来越受到人们的重视.地球内部的各向异性介质广泛存在,在各向异性介质中采用各向同性介质模型进行逆时偏移,通常会导致成像精度降低,比如反射波归位不准,能量不聚焦等.为进一步完善逆时偏移技术,在保证计算精度和效率前提下,有必要考虑各向异性介质的影响.各向异性介质的波场模拟和逆时偏移可以通过弹性波方程数值模拟实现,但是,不仅各向异性介质的弹性波方程较为复杂,目前也尚难彻底分离纵横波波场,而且计算成本很高,这无疑对高成本的逆时偏移又提出了更高的计算要求.为避免弹性波数值求解,本文研究了各向异性介质的准P波方程.垂直横向各向同性介质(Transversely Isotropic media with a Vertical symmetry axis,VTI)是一种常用的各向异性介质模型.因此研究VTI介质一阶准P波逆时偏移方法意义重要,对其他类各向异性介质的高精度逆时偏移也具有启示意义.
目前,存储量大、计算成本高以及低频噪音仍是限制逆时偏移技术发展的主要问题.近年来,多名学者提出或改进了RTM的存储方案,Symes(Symes,2007)提出了用checkpointing技术来降低波场存储量的思想;Dussaud(Dussaud et al.,2008)等比较了几种常用的存储策略,认为checkpointing技术降低了波场存储量的同时较明显增加了计算量;Clapp(Clapp,2008,2009)提出了随机边界存储方法,在很大程度上节约了存储量.王保利(王保利等,2012)等详细比较了几种常用的边界存储策略,提出了有效边界存储策略.胡昊(胡昊等,2013)对比分析了随机边界和单层吸收边界,认为随机边界会出现边界漫反射,单层吸收边界会损失部分能量等.康玮(康玮和程玖兵,2012)分析了叠前逆时偏移低频噪音干扰去除的一些常用方法,认为基于GPU平台的逆时偏移,采用Laplace去噪是目前最经济的选择.最近几年图形处理器(Graphic Processing Unit)的迅猛发展为浮点数据计算带来了大幅度的效率提升.刘红伟(刘红伟等,2010)和李博(李博等,2010)等借助GPU加速技术实现了有限差分逆时偏移算法,提极大地提高了计算效率.为解决各向异性介质弹性波数值模拟的问题,Alkhalifah(Alkhalifah,1998,2000)提出了声波近似思想,给出了VTI介质四阶波动方程和二阶方程组.研究表明,声学近似对纵波的运动学特征几乎无影响,同时避免了弹性波数值模拟的缺陷.在Alkhalifah研究的基础上,一些研究人员给出了其他形式的二阶偏微分方程组(Klié and Toro,2001; Zhou et al.,2006; Hestholm,2007; Du et al.,2008; Duveneck et al.,2008).Hestholm(Hestholm,2009)对二阶VTI方程组进行了数学变换,组合成为六个一阶耦合偏微分方程.Zhou(Zhou et al.,2006),Fletcher(Fletcher et al.,2009),Fowler(Fowler et al.,2010)等利用声波近似原理推导出了TTI介质拟声波方程.Bube(Bube et al.,2012),Zhang(Zhang and Zhang,2009; Zhang and Sun,2009),Bakker(Bakker and Duveneck,2011)等针对TTI介质波场模拟不稳定现象,提出了一些改进的思想以及技术方法.张岩(张岩和吴国忱,2013)回顾了各向异性介质逆时偏移发展历史,对TTI介质叠前逆时偏移成像的研究现状、进展进行了概述.沈铭成(沈铭成等,2014)针对VTI介质声学近似带来的伪横波干扰以及算法稳定性问题,提出了VTI介质的解耦合声波近似方程,该方程可以使qp波波场传播更稳定,同时消除了伪sv波的干扰.程玖兵(程玖兵等,2013,2014)研究了各向异性介质qp波传播模式:伪纯模式波动方程和分离纯模式标量波,为各向异性介质的分离模式的波场的传播过程提供了描述工具.
交错网格(Virieux,1984)相对于常规网格精度高,本文在Hestholm(Hestholm,2009)研究的基础上,推导出了该方程组炮点和检波点逆时延拓的交错网格高阶有限差分格式,针对算法计算量大、存储量大的问题,给出了基于GPU平台的改进有效完全匹配层(PML)吸收边界条件,不仅提高了计算效率同时降低了存储量.应用震源归一化互相关成像条件,利用拉普拉斯算子去除低频噪音,利用Hess 2DVTI模型证明本文方法的正确性及有效性.
1 VTI介质一阶准P波方程组炮点和检波点逆时延拓1.1 Hestholm给出的二维VTI介质中一阶准P波方程组




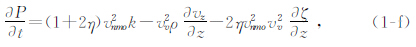
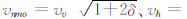
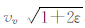 ,η是各项异性参数,
,η是各项异性参数,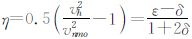 ,ε、δ为Thomsen参数(Thomsen,1986).
1.2 交错网格差分格式及完全匹配层(PML)控制方程
,ε、δ为Thomsen参数(Thomsen,1986).
1.2 交错网格差分格式及完全匹配层(PML)控制方程
利用交错网格(董良国等,2000)对式(1)进行有限差分离散,推导出准P波的逆时延拓差分格式(本文只离散式(1-a)、(1-f),同理可对其他式离散):

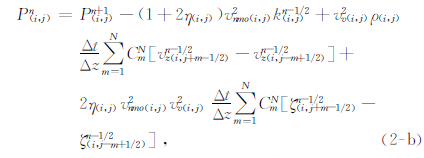
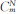 为交错网格差分系数.
为交错网格差分系数.
基于PML边界条件的分裂思路(王守东,2003),对式(1)研究区域四周引入完全匹配层,可以得到完全匹配层控制方程,本文只对式(1-a)、(1-f)进行匹配层引入,同理可得其余式匹配层控制方程为

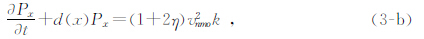
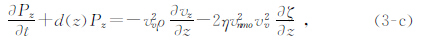

同理对式(3)进行交错网格有限差分格式离散,可以得到完全匹配层正向延拓和逆时延拓交错网格差分格式.
1.3 二维VTI介质中一阶准P波交错网格数值模拟稳定性条件对于时间2阶差分精度,空间2N阶差分精度的一阶准P波交错网格差分格式,本文采用的稳定性条件(董良国等,2000)为

 为交错网格差分系数.
2 基于GPU加速的有效PML吸收边界条件存储策略
为交错网格差分系数.
2 基于GPU加速的有效PML吸收边界条件存储策略
逆时偏移方法包括正传波场计算、反传波场计算以及二者的零延迟互相关成像,若保存全部历史时刻的正传波场,会出现较大的存储需求.例如:2000×1000网格点数的速度模型,时间采样点数取10000,存储数据类型是4字节浮点型,则需要约80 Gb来存储所有时刻的正传波场,目前的计算机硬件几乎无法承受.高存储成本是限制逆时偏移技术发展的主要障碍,计算机硬件技术的发展在一定程度上可以带动存储能力的提高,但是,仍需寻求有效降低存储的逆时偏移算法.鉴于此,本文提出了改进的基于GPU加速的PML吸收边界存储策略,其可在降低存储成本的同时,实现高效率、高精度的叠前逆时偏移成像.
2.1 改进的PML边界存储方法PML吸收边界条件使波场在PML吸收层衰减,是目前效果最好的边界吸收条件.本文针对交错网格,研究了一种改进的PML边界存储方法,该方法存储量小、计算成本低、吸收效果好.该方法借鉴了随机边界逆向传播震源波场的思想,保存和利用最后两个时刻的震源波场,有别于随机边界方法的是,文中方法也存储正向传播的各时刻边界波场.首先,在震源波场正向传播的过程中把边界的波场存储起来,然后,在后两时刻的波场逆时回推前一时刻的波场的过程中,用存储的边界波场代替逆时回推过程的边界波场,这样可以保证在模拟计算区域,每个时刻波场都具有完整的能量,因此后两时刻的波场可以恢复前一时刻的波场.
王保利(王保利等,2012)提出了有效边界存储策略,其方法是修改波场逆向传播的边界条件,保存PML区域内的若干层内所有时刻的波场值,利用最后两个时刻波场通过反传播技术得到之前任意时刻的正确的波场.其边界波场存储方案如图 1所示:虚线框包括了PML吸收边界和内部模拟计算区域,虚线和相邻的的实线框所组成的白色区域为PML吸收边界层,两个实线框所组成的灰色区域为要记录的边界波场,实线边框内是不包括吸收边界的计算区域.本文提出了一种改进方法,如图 2所示,相比于图 1所示的存储方案,本文改进方法所存储的边界波场是计算区域的波场,而非PML吸收边界区域的波场,边界波场在内部模拟计算区域,不会有任何能量衰减,也在减少存储量的同时,缩短了读写边界波场的时间.
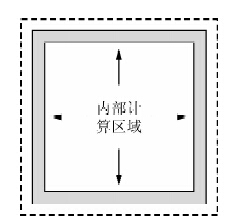
| 图 1 有效PML边界示意图 Fig. 1 Efficient PML boundary diagram |
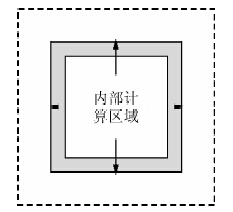
| 图 2 改进的PML边界示意图 Fig. 2 Improved PML boundary diagram |
下面将详细的介绍改进的PML边界存储策略以及VTI介质一阶准P波的逆时偏移实现过程.公式(2)为推导出来的VTI介质一阶准P波交错网格差分格式,包括六个相互耦合的变量:波场P,速度分量vx、vz,三个辅助波场κ、ζ、φ.应力波场P的变化会导致速度分量vx、vz的更新,对于空间2N阶差分,需要保存边界N个节点的应力波场P,这样利用波场P逆时回推前一时刻的速度分量vx、vz的过程中,利用存储的边界N个节点的应力波场P,代替逆时回推过程的N个节点的应力波场P,这样可以准确的更新内部模拟计算区域速度分量vx、vz.如图 3所示:内部计算区域红色虚线框内为保存的若干节点的边界波场P.同理还需要存储边界N个节点的vx、vz、κ、ζ、φ这些变量的值.举例来说:空间12阶精度的交错网格差分格式,需要存储边界6个节点的应力波场P,利用波场P逆时回推速度分量vx、vz的过程中,利用存储的6个边界节点的应力波场P,赋值给逆时回推过程的6个边界节点的应力波场P,这可以保证更新的速度分量vx、vz是正确的.同理需要存储边界6个节点的vx,在逆时回推过程中重新赋值给边界6个节点的vx来更新辅助变量波场κ等等.在算法实现的过程中,需要存储P、vx、vz、κ、ζ、φ六个边界波场,但是,保存边界波场太多会导致编程过程繁琐.分析公式知,这六个波场变量具有相互依赖关系,如果保证内部模拟计算区域应力波场P能量的完整性,在逆时回推过程中,就可以保证依赖应力波场P的其他波场变量的正确.对于空间2N阶差分精度交错网格差分格式(2),保存边界2N-1个节点的应力波场P,在逆时回推过程中,利用存储的边界2N-1个节点的应力波场P,代替逆时回推过程的2N-1个节点的应力波场P,这样可以在更新波场变量的过程中,保证其他五个波场变量的正确.相对于存储P、vx、vz、κ、ζ、φ六个边界波场,只存储波场变量P的边界波场,既简化了算法,也节约了波场变量的存储空间.
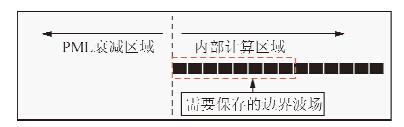
| 图 3 改进的PML边界波场存储示意图 Fig. 3 Improved efficient PML boundary wave field storage diagram |
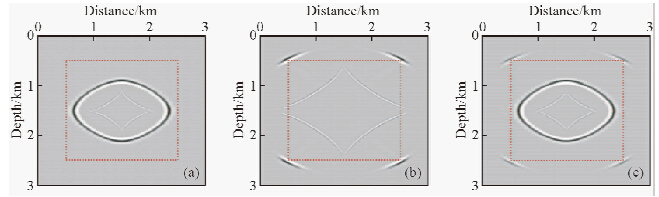
为验证改进的PML边界条件能否正确逆时回推震源波场,设计了200×200网格的均匀各向异性介质,其中各向异性参数η为0.5,动校正速度和垂向速度均为3000 m/s,完全匹配层(PML)厚度为50个网格.算法采用时间上二阶精度、空间上十二阶精度的交错网格差分格式,空间步长为10 m,时间步长为0.5 ms.图 4为模拟的不同时刻的震源波场快照,震源位于模型的中间位置,时间总采样点数为1000.图 4a为0.25 s的正传震源波场快照,图 4b为最大时刻0.5 s的震源波场快照,图 4c为利用本文提出的改进的PML边界条件从最大时刻0.5 s逆时回推的0.25 s的波场快照.对比可知,模型内部计算区域的波场可以通过最后时刻的波场逆时回推完整的恢复出来.
|
图 4 均匀各向异性介质模型波场快照 (a)震源正向传播0.25s的波场快照;(b)震源正向传播的最大时刻0.5s的波场快照;(c)利用改进的有效PML吸收边界条件逆时回传的0.25s的波场快照. Fig. 4 The snapshot of homogeneous anisotropic medium model (a)The wave field snapshot of source forward propagation at 0.25 seconds; (b)The wave field snapshot of source forward propagation at 0.5 seconds; (c)The wave field snapshot of source wave field reverse-time propagation at 0.25 seconds by the improved PML absorbing boundary condition. |
相对于CPU,GPU在处理能力和存储器带宽上有明显的优势,GPU可以通过增加并行处理单元和存储器控制单元来提高处理能力和存储器带宽.GPU加速的性能受并行算法和GPU硬件构架的影响,程序优化程度的好坏影响计算效率.GPU通过PCI-E总线和主机相连,GPU输入和输出的吞吐量受到IO带宽的限制.由于PCI-E带宽相对较小,为提高程序的计算效率,应该尽量减小CPU和GPU间数据传输量.当需要存储的边界波场较小时,可以把边界波场全部存储在显存中,在设备端(GPU)进行逆时回推计算时,直接用存储在设备端的边界波场代替逆时回推过程中的边界波场;当时间离散点数很大时,需要存储的边界波场会超出设备端(GPU)的显存容量,需要把边界波场存储在主机端内存中,通过PCI-E总线进行CPU和GPU间数据传输.为了减小CPU和GPU间的数据传输量,提高计算效率,可以采取如下策略:在正演过程中设置NC个checkpoint时间点,在每个checkpoint时间点处保存该时刻的全部波场,把这些checkpoint时间点处的波场保存到主机端内存中,在设备端只保存相邻两个checkpoint时间点之间的边界波场,实现过程如图 5.对比于把全部边界波场保存于主机端内存这种方法,图 5所示的这种策略可以减小CPU和GPU间的数据传输量,同时没有增加计算量.针对公式(2),我们在checkpoint离散时间点处,需要保存的完整波场有P、vx、vz、κ、ζ、φ.图 6为基于GPU加速平台,同时结合改进的PML边界存储策略实现的逆时偏移算法流程图.

| 图 5 不同时刻的全波场和边界波场保存示意图 Fig. 5 Full wave field and the boundary wave field at different time |

| 图 6 改进的PML吸收边界条件逆时偏移流程图 Fig. 6 Flow chart of reverse-time migration by improved PML absorbing boundary condition |
图 7a为Hess 2DVTI速度模型,逆时偏移算法采用了交错网格有限差分格式,时间采用二阶精度、空间采用十二阶精度,网格间距为dx=10 m、dz=10 m,时间步长为0.3 ms,震源位置位于地表18千米处.图 7b、图 7c为震源波场正传1.5 s时刻和采用改进PML边界存储策略逆时回推1.5 s时刻波场快照对比图.分析图 7b和图 7c可以看出,有效PML边界存储策略可以通过最后时刻的波场逆时回推完整的恢复内部模拟计算区域的波场.沿图 7b和7c中红线位置,抽取快照波场的一部分对比分析,如图 7d和7e所示,改进的PML边界存储策略,可以使模型内部计算区域的波场完整的恢复出来,同时恢复出来的震源波场同震源正向传播的波场振幅差可以忽略,几乎没有能量损失.表 1为离散采样时间点数nt=1000时,上述Hess 2DVTI模型正演模拟分别采用CPU计算和CPU/GPU并行计算的耗时对比.从表 1中可以看出,CPU/GPU并行加速计算技术可以使Hess 2DVTI模型的正演效率提高100倍.

|
图 7 Hess 2DVTI模型正向传播震源波场和逆时回传震源波场 (a)Hess 2DVTI速度模型;(b)(c)分别为震源正向传播的1.5 s和改进的PML吸收边界条件逆时回传的1.5 s波场快照;(d)(e)分别为部分波场快照振幅对比. Fig. 7 Hess 2DVTI model of forward propagation source wave field and reverse-time propagation source wave field (a)Hess 2DVTI velocity model;(b)(c)respectively,the wave field snapshot of source forward propagation at 1.5 seconds and the wave field snapshot of source wavefield reverse-time propagation at 1.5 seconds by the improved PML absorbing boundary(d)(e)respectively,the amplitude comparison of some wave field snapshot. |
|
|
表 1 GPU加速效率 Table 1 The efficiency of GPU acceleration |
Hess 2DVTI 模型左部有一个高速盐丘体,中部有有尖灭构造,右部有较为陡峭的倾斜断层,中部的尖灭构造是成像难点.模型参数包括纵波速度、各向异性参数ε、变异系数δ.逆时偏移算法采用时间二阶、空间十二阶的交错网格有限差分格式,网格间距dx和dz均为10 m,时间步长为0.3 ms.该模型的纵波速度如图 7a所示,图 8a为模型各向异性参数ε,图 8b为模型变异系数δ,图 8c为单炮逆时偏移成果图、其中炮点位于地表18km处,图 8d为图 8c经过拉普拉斯算子滤波去除低频噪音的结果图,图 8e为2D Hess VTI模型360炮叠加的逆时偏移成果图.表 2为取Hess 2DVTI 模型的大小为3000×1500网格,离散时间点数nt=15000时几种不同的逆时偏移存储策略的计算量和存储量的对比,其中NC代表checkpoint时间点数.可以看出有效PML边界存储显著地降低了波场的存储量.
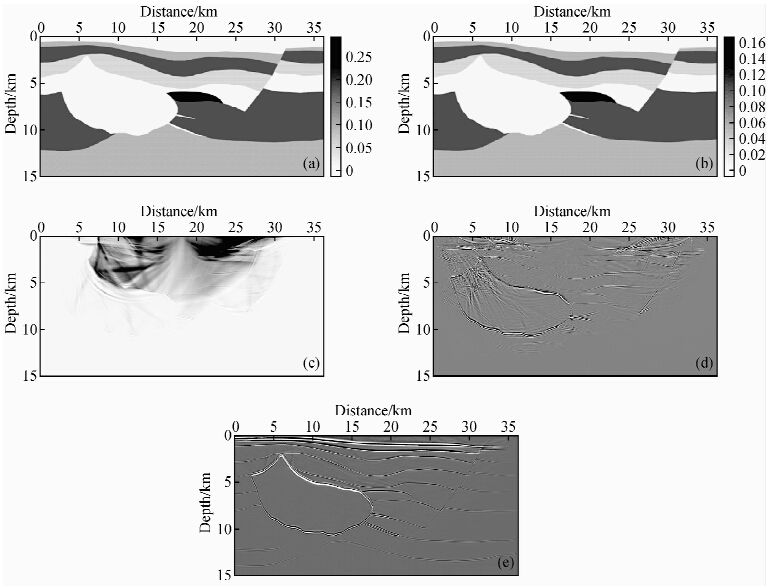
| 图 8 (a)Hess 2DVTI各向异性参数ε;(b)Hess 2DVTI变异系数δ;(c)Hess 2DVTI 单炮逆时偏移; (d)Hess 2DVTI 单炮逆时偏移施加Laplace滤波;(e)Hess 2DVTI 逆时偏移. Fig. 8 (a)Hess 2DVTI anisotropic parameter ε;(b)Hess 2DVTI anisotropic parameter δ;(c)RTM for Hess 2DVTI model with a single shot;(d)RTM for Hess 2DVTI model with a single shot and Laplace filtering;(e)RTM for Hess 2DVTI model. |
|
|
表 2 Hess 2DVTI模型不同边界存储策略对比 Table 2 Comparison of different boundary storage strategy of Hess 2DVTI model |
叠前逆时偏移是一种高精度地震成像方法,非常适合于复杂构造成像,但是方法本身对计算机硬件要求较高.地球介质各向异性广泛存在,考虑各向异性介质影响的逆时偏移技术是必要的,GPU的出现也促进了逆时偏移技术的发展.本文研究了VTI介质的逆时偏移技术,针对存储量大的问题,给出了基于GPU加速平台的改进的PML边界存储策略,有效地降低了波场存储成本,也大幅度提升了算法的计算效率.相对于传统的逆时偏移技术,本文提出的基于改进PML边界存储的VTI介质逆时偏移方法可以给出高精度的成像剖面,同时极大地节约存储空间.结合GPU加速技术,文中方法也可高效率完成复杂构造逆时偏移成像.
致 谢 本文部分研究内容受到东北石油大学研究生创新科研项目(YJSCX2014-005NEPU)项目资助,在此表示感谢.| [1] | Alkhalifah T. 1998. Acoustic approximations for processing in transversely isotropic media[J]. Geophysics, 63(3) 623-631. |
| [2] | Alkhalifah T. 2000. An acoustic wave equation for anisotropic media[J]. Geophysics, 65(4):1239-1250. |
| [3] | Bakker P M, Duveneck E. 2011. Stability analysis for acoustic wave propagation in tilted TI media by finite differences[J]. Geophys. J. Int., 185(2):911-921. |
| [4] | Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration[J]. Geophysics, 48(11):1514-1524. |
| [5] | Bube K P, Nemeth T, Stefani J P, et al. 2012a. First-order systems for elastic and acoustic variable-tilt TI media[J]. Geophysics, 77(5):T157-T170. |
| [6] | Bube K P, Nemeth T, Stefani J P, et al. 2012b. On the instability in second-order systems for acoustic VTI and TTI media[J]. Geophysics, 77(5):T171-T186. |
| [7] | Cheng J B, Kang W, Wang T F. 2013. Description of qP-wave propagation in anisotropic media, Part I:Pseudo-pure-mode wave equations[J]. Chinese J. Geophys. (in Chinese), 56(10):3474-3486, doi:10.6038/cjg20131022. |
| [8] | Cheng J B, Chen M G, Wang T F, et al. 2014. Description of qP-wave propagation in anisotropic media, Part Ⅱ:Separation of pure-mode scale waves[J]. Chinese J. Geophys. (in Chinese), 57(10):3389-3401, doi:10.6038/cjg20141025. |
| [9] | Clapp R G. 2008. Reverse time migration:Saving the boundaries[J], 136:136-144. |
| [10] | Clapp R G. 2009. Reverse time migration with random boundaries[C].//79th Annual International Meeting, SEG. Expanded Abstracts, 2809-2813. |
| [11] | Dong L G, Ma Z T, Cao J Z, et al. 2000. A staggered-grid high-order difference method of one-order elastic wave equation[J]. Chinese J. Geophys. (in Chinese), 43(3):411-419. |
| [12] | Du X, Fletcher R P, Fowler P J. 2008. A new pseudo-acoustic wave equation for VTI media[C].//70th Annual Conference and Exhibition, EAGE. Extended Abstracts, H033. |
| [13] | Dussaud E, Symes W W, Williamson P, et al. 2008. Computational strategies for reverse-time migration[C].//78rd Annual International Meeting, SEG. Expanded Abstracts, 27:2267-2271. |
| [14] | Duveneck E, Milcik P, Bakker P M, et al. 2008. Acoustic VTI wave equations and their application for anisotropic reverse-time migration[C].//78th Annual International Meeting, SEG. Expanded Abstracts, 2186-2190. |
| [15] | Fletcher R P, Du X, Fowler P J. 2009. Reverse time migration in tilted transversely isotropic (TTI) media[J]. Geophysics, 74(6):WCA179-WCA187. |
| [16] | Fowler P J, Du X, Fletcher R P. 2010. Coupled equations for reverse time migration in transversely isotropic media[J]. Geophysics, 75(1):S11-S22. |
| [17] | Hestholm S. 2007. Acoustic VTI modeling using high-order finite-differences[C].//77th Annual International Meeting, SEG. Expanded Abstracts, 139-143. |
| [18] | Hestholm S. 2009. Acoustic VTI modeling using high-order finite differences[J]. Geophysics, 74(5):T67-T73 |
| [19] | Hu H, Liu Y K, Chang X, et al. 2013. Analysis and application of boundary treatment for the computation of reverse-time migration[J]. Chinese J, Geophys. (in Chinese), 56(6):2033-2042, doi:10.6038/cjg20130624. |
| [20] | Kang W, Cheng J B. 2012. Methods of suppressing artifacts in prestack reverse time migration[J]. Progress in Geophys. (in chinese), 27(3):1163-1172, doi:10.6038/j.issn.1004-2903.2012.03.041. |
| [21] | Klié H, Toro W. 2001. A new acoustic wave equation for modeling in anisotropic media[C].//71st Annual International Meeting, SEG. Expanded Abstracts, 1171-1174. |
| [22] | Li B, Liu H W, Liu G F, et al. 2010. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU[J]. Chinese J. Geophys. (in Chinese), 53(12):2938-2943, doi:10.3969/j.issn.0001-5733.2010.12.017. |
| [23] | Liu H W, Li B, Liu H, et al. 2010. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation[J]. Chinese J. Geophys. (in Chinese), 53(7):1725-1733, doi:10.3969/j.issn.0001-5733.2010.07.024. |
| [24] | Liu Y, Li C C, Mou Y G. 1998. Finite-difference numerical modeling of any even-order accuracy[J]. Oil Geophysical Prospecting (in Chinese), 33(1):1-10. |
| [25] | Loewenthal D, Stoffa P A, Faria E L. 1987. Suppressing the unwanted reflections of the full wave equation[J]. Geophysics, 52(7):1007-1012. |
| [26] | McMechan G A. 1983. Migration by extrapolation of time-dependent boundary values[J]. Geophysical Prospecting, 31(3):413-420. |
| [27] | Shen M C, Li L M, Zhou H L. 2014. Numerical simulation of decoupled VTI media acoustic wave equation[J]. Progress in Geophysics (in Chinese), 29(3):1218-1223, doi:10.6038/pg20140330. |
| [28] | Symes W W.2007.Reverse time migration with optimal checkpointing[J]. Geophysics, 72(5):SM213- SM221. |
| [29] | Thomsen L. 1986. Weak elastic anisotropy[J]. Geophysics, 51(10):1954-1966. |
| [30] | Virieux J. 1984. SH-wave propagation in heterogeneous media:velocity-stress finite-difference method[J]. Geophysics, 49(11):1933-1942. |
| [31] | Wang B L, Gao J H, Chen W C, et al. 2012. Efficient boundary storage strategies for seismic reverse time migration[J]. Chinese J. Geophys. (in Chinese), 55(7):2412-2421, doi:10.6038/j.issn.0001-5733.2012.07.025. |
| [32] | Wang S D. 2003. Absorbing boundary condition for acoustic wave equation by perfectly matched layer[J]. Oil Geophysical Prospecting (in Chinese), 38(1):31-34. |
| [33] | Whitmore N D. 1983. Iterative depth migration by backward time propagation[C].//53rd Annual International Meeting, SEG. Expanded Abstracts, 827-830. |
| [34] | Zhang Y, Zhang H Z. 2009. A stable TTI reverse time migration and its implementation[C].//79th Annual International Meeting, SEG. Expanded Abstracts, 2794-2798. |
| [35] | Zhang Y, Sun J. 2009. Practical issues in reverse time migration:true amplitude gathers, noise removal and harmonic-source encoding[J]. First Break, 26(1):29-35. |
| [36] | Zhang Y, Wu G C. 2013. Review of prestack reverse-time migration in TTI media[J]. Progress in Geophys. (in Chinese), 28(1):409-420, doi:10.6038/pg20130146. |
| [37] | Zhou H B, Zhang G Q, Bloor R. 2006a. An anisotropic acoustic wave equation for VTI media[C].//68thAnnual Conference and Exhibition, EAGE. Extended Abstracts, H033. |
| [38] | Zhou H B, Zhang G Q, Bloor R. 2006b. An anisotropic acoustic wave equation for modeling and migration in 2D TTI media[C].//76th Annual International Meeting, SEG. Expanded Abstracts, 194-198. |
| [39] | 程玖兵,康玮,王腾飞. 2013.各向异性介质qP波传播描述Ⅰ:伪纯模式波动方程[J].地球物理学报, 56(10):3474-3486, doi:10.6038/cjg20131022. |
| [40] | 程玖兵,陈茂根,王腾飞,等. 2014.各向异性介质qP波传播描述Ⅱ:分离纯模式标量波[J].地球物理学报, 57(10):3389-3401, doi:10.6038/cjg20141025. |
| [41] | 董良国,马在田,曹景忠,等. 2000.一阶弹性波方程交错网格高阶差分解法[J].地球物理学报, 43(3):411-419. |
| [42] | 胡昊,刘伊克,常旭,等. 2013.逆时偏移计算中的边界处理分析及应用[J].地球物理学报, 56(6):2033-2042, doi:10.6038/cjg20130624. |
| [43] | 康玮,程玖兵. 2012.叠前逆时偏移假象去除方法[J].地球物理学进展, 27(3):1163-1172, doi:10.6038/j.issn.1004-2903.2012.03.041. |
| [44] | 李博,刘红伟,刘国峰,等. 2010.地震叠前逆时偏移算法的CPU/GPU实施对策[J].地球物理学报, 53(12):2938-2943, doi:10.3969/j.issn.0001-5733.2010.12.017. |
| [45] | 刘红伟,李博,刘洪,等. 2010.地震叠前逆时偏移高阶有限差分算法及GPU实现[J].地球物理学报, 53(7):1725-1733, doi:10.3969/j.issn.0001-5733.2010.07.024. |
| [46] | 刘洋,李承楚,牟永光. 1998.任意偶数阶精度有限差分法数值模拟[J].石油地球物理勘探, 33(1):1-10. |
| [47] | 沈铭成,李录明,周怀来. 2014. VTI介质解耦合声波方程数值模拟[J].地球物理学进展, 29(3):1218-1223, doi:10.6038/pg20140330. |
| [48] | 王保利,高静怀,陈文超,等. 2012.地震叠前逆时偏移的有效边界存储策略[J].地球物理学报, 55(7):2412-2421, doi:10.6038/j.issn.0001-5733.2012.07.025. |
| [49] | 王守东. 2003.声波方程完全匹配层吸收边界[J].石油地球物理勘探, 38(1):31-34. |
| [50] | 张岩,吴国忱. 2013. TTI介质叠前逆时偏移成像研究综述[J].地球物理学进展, 28(1):409-420, doi:10.6038/pg20130146. |
 2015, Vol. 30
2015, Vol. 30


