在大地电磁勘探中,倾子(也称垂直磁场转换函数)表示磁场水平分量和垂直分量的相互关系,作为大地电磁阻抗张量或视电阻率和相位资料的重要辅助数据,定性判断地下构造的维数和走向,已经广泛地应用于深部地质构造调查、火山地震结构探测等方面(陈乐寿,1989;刘国栋和陈乐寿,1993).近年来,一方面随着大地电磁仪器的不断改进和完善,尤其是高温超导量子干涉磁力仪的出现,使得采集磁场垂直分量变得越来越可靠(马平等,2001;丁红胜等,2004;陈晓东等,2012),另一方面随着大地电磁数据处理不断成熟和发展,倾子资料直接参与二维、三维反演成为可能.因此迫切的需要对倾子资料的三维正反演及响应特征进行研究,为倾子资料从定性解释向定量解释发展提供参考和依据.
受野外资料采集的影响,前期对大地电磁倾子的研究工作相对较少.较早的研究工作为倾子资料特征及其应用(胡文宝等,1997;陈小斌等,2004),研究认为倾子异常主要反映了地电结构的横向非均匀性,且可作为定性判别某点电性结构二维性的一种衡量标准;之后倾子资料被应用到一些特殊地电结构(如埋藏球体、板状体和断裂等)的识别和解释中(陈清礼等,2007;余年等,2007;柳建新等,2012;吴頔,2012),在分析倾子的响应特征的基础上,总结出了在二维地电模型中,大地电磁测深倾子资料能很好地反映地下结构水平方向的不均匀性,为倾子资料对构造识别提供了判别依据;与此同时,不同条件下(影响因素)倾子的响应特征(童孝忠等,2011;甘佳雄,2012;席振铢,2013;徐凌华等;2013)也得到了广泛研究.然而,他们的研究工作主要集中在二维倾子的响应特征上(余年,2012),三维倾子资料的研究很少(林昌洪等,2011),而且缺乏复杂地电条件下三维倾子响应的研究,影响了以倾子为参数的大地电磁资料解释的实用进程.
综上所述,本文在前人基于交错网格有限差分法的大地电磁三维正演基础上(谭捍东等,2003,2004;陈辉等,2011),通过推导倾子的数值模拟计算公式,实现大地电磁三维倾子数据正演.在此基础上对几个典型地电模型的倾子响应特征进行模拟,归纳和总结大地电磁倾子的三维响应特征,为大地电磁倾子资料的野外勘探和数据解释提供参考和借鉴.
1 大地电磁三维倾子正演模拟 1.1 大地电磁基于磁场的三维数值模拟由大地电磁法理论可知,在准静态条件下频率域内的Maxwell方程组积分形式为:
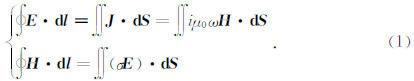
对求解区域在直角坐标系下采用YEE网格剖分,对方程组(1)中两式利用有限差分进行离散得到电场分量与磁场分量之间的关系式,消去电场分量得到关于磁场各分量的关系式.采用第一类边界条件,建立关于磁场各分量的线性方程组 Ax=b .采用不完全LU分解的预处理双共轭梯度稳定算法进行求解得到磁场各分量的解.
1.2 大地电磁三维倾子计算大地电磁法是一种天然场源的频率域电磁测深法,在野外通常观测两个相互垂直的电场分量和磁场分量,加上一个垂向磁场方向.倾子也称垂向磁场转化函数,表示磁场水平分量与垂直分量之间的关系,在直角坐标系中,倾子矢量定义关系式为:




为了了解不同条件下三维大地电磁的倾子响应特征,分别设计了单个低阻和单个高阻异常体模型,通过三维正演计算了其倾子实、虚部和幅值的三维响应特征,然后对含多异常体组合地电模型的倾子异常响应进行分析研究.
2.1 单个异常体模型构造地电模型如图 1所示,图 1a为低(高)阻异常体模型水平截面图,图 1b为低(高)阻异常体模型垂直截面图.设围岩的电阻率为100 Ω·m,低阻异常体的电阻率为ρ1=10 Ω·m,大小为3000 m×3000 m×3000 m,顶部埋深为1500 m,且关于X=0对称,模拟测点数为49个,记录频点数为49个(2.16×10-4~1.0×103 Hz);同时参照图 1另设一高阻异常体模型,设高阻异常体的电阻率为ρ2=1000 Ω·m,其他参数设置与低阻异常体模型相同.通过三维数值模拟,计算得出低、高阻两种地电模型倾子实部、虚部、振幅响应断面图,如图 2 所示.
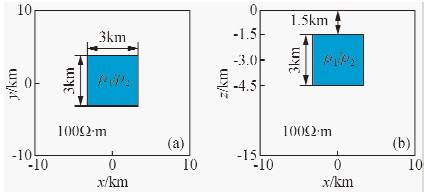 |
图 1 单个异常体模型示意图 (a)单个异常体水平截面示意图;(b)单个异常体垂直截面示意图. Fig. 1 Sketch of single abnormal body model (a) Horizontal section diagram;(b) Vertical section diagram. |
 |
图 2 低阻异常体三维倾子响应图 (a) Tx倾子实部;(b) Ty倾子实部;(c) Tx倾子虚部;(d) Ty倾子虚部;(e) Tx倾子幅值;(f) Ty倾子幅值. Fig. 2 3D tipper response diagram for low resistivity abnormal body (a) Re (Tx);(b) Re (Ty);(c) Im (Tx);(d) Im (Ty);(e) Am (Tx);(f) Am (Ty). |
图 2a、2c、2e分别为低阻异常体Tx实部、虚部和幅值响应断面图,图 2b、2d、2f分别为低阻异常体Ty实部、虚部和幅值断面图;其中倾子实、虚部和幅值单位均为1,且幅值大小为取对数后的值(下文同).从图 2a可以看出,低阻异常体模型的Tx倾子实部资料表现出高值异常区,低阻异常体左右边界分别位于高值异常区左右两侧的边缘,并关于X=0对称;而对于Ty倾子实部资料(图 2b),横向上表现出关于X=0呈反对称形态(即X=0线一侧异常区表现为高值时,对应的另一边则表现为低值,反之亦然)的一低一高的异常区,异常体左边界介于最低值区域等值线的接触带上,右边界则位于最高值区域等值线的接触带上.
相应地,对于高阻异常体模型而言,它的Tx实部资料(见图 3a)表现出低值异常区,异常体左右边界分别位于低阻异常区左右两侧的边缘,而Ty实部资料(图 3b)横向上表现为与低阻异常体模型Ty实部资料相反的一高一低异常区,高阻异常体的左边界介于最高值区域等值线的接触带上,而右边界则介于最低值区域等值线的接触带上.
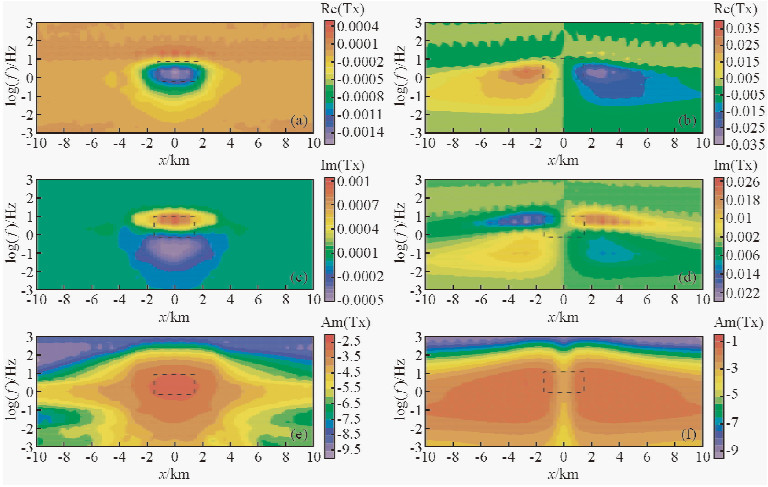 |
图 3 高阻异常体三维倾子响应图 (a) Tx倾子实部;(b) Ty倾子实部;(c) Tx倾子虚部;(d) Ty倾子虚部;(e) Tx倾子幅值;(f) Ty倾子幅值. Fig. 3 3D tipper response diagram for high resistivity abnormal body (a) Re (Tx);(b) Re (Ty);(c) Im (Tx);(d) Im (Ty);(e) Am (Tx);(f) Am (Ty). |
低阻模型Tx虚部资料(图 2c)纵向上表现为一低一高的异常区,低阻异常体的上下边界分别沿着低值和高值区域延伸,左右边界在中高频段位于低值区域等值线的边缘,在中低频段则位于高值区域等值线的边缘上;Ty虚部资料(图 2d)在中高频段和中低频段均表现出与实部资料对应的反对称形态,在中高频段,异常体的左右边界分别介于高值区域等值线的接触带和低值区域等值线的接触带上,在低频段则相反.对于高阻模型,其异常特征刚好与低阻异常体相反,在中高频段,异常体的左右边界分别介于低值区域等值线的接触带和高值区域等值线的接触带上,在低频段则恰好相反.
低阻模型和高阻模型的Tx和Ty幅值资料(图 2e、2f、3e、3f)的表现形态一致,Tx幅值资料都表现为高值异常区,且异常体的上下边界都沿着高值异常区等值线的接触带延伸;Ty幅值资料从左至右表现出关于异常体中心线对称的两个高值异常区异常体左右边界均沿着高值异常区延伸.
在对比分析了低阻和高阻地电模型的三维倾子响应特征之后,本文同时以低阻为例,分别绘出低阻模型在最佳观测频率(f=2.15 Hz)上倾子虚、实部和幅值的平面图,如图 4所示,从图中可以看出,Tx和Ty的虚、实部和幅值响应在最佳观测频率效果明显,且相互对称,进一步突出倾子在大地电磁解释中的可靠性和有效性.综上所述,单个异常体的大地电磁三维倾子响应特征明显,结合倾子响应的断面图和平面图能很好的确定异常体的边界.
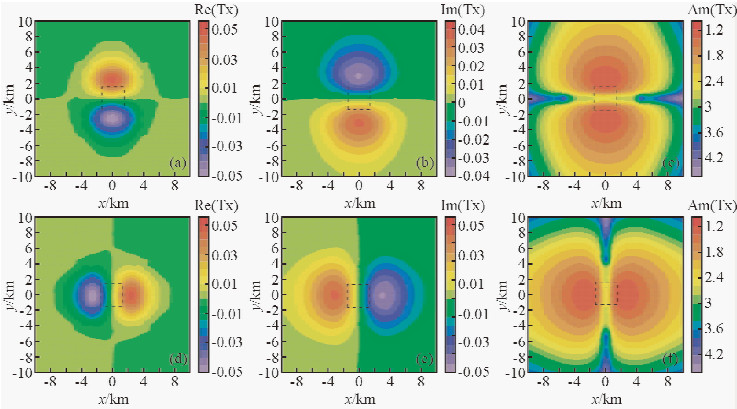 |
图 4 低阻异常体最佳观测频点响应图 (a) Tx倾子实部;(b) Tx倾子虚部;(c) Tx倾子幅值;(d) Ty倾子实部;(e) Ty倾子虚部;(f) Ty倾子幅值. Fig. 4 Response diagram of the low resisitivity abnormal body at the best observation frequency (a) Re (Tx);(b) Im (Tx);(c) Am (Tx);(d) Re (Ty);(e) Im (Ty);(f) Am (Ty). |
给定的地电模型为含有两个低(高)阻和一个低阻垂直断层组合模型(图 5),其中组合模型一设模型围岩电阻率为100 Ω·m,两个低阻异常体的电阻率均为ρ1 =10 Ω·m,大小为4000 m×4000 m×4000 m,顶部埋深为1500 m;低阻垂直断层电阻率也为10 Ω·m,宽度为1000 m,X=0与垂直断层的中心线重合,两个低阻异常体关于X=0对称;组合模型二将模型一中的两个低阻异常体换成对应的两个高阻异常体,电阻率为ρ2=1000 Ω·m,其他模型参数设置与模型一相同,它们的倾子响应结果分别如图 6和图 7所示.从图中可以看出,两种组合模型的倾子响应对每个异常体均有较好的反映,且异常区分界面明显,能易于确定低(高)阻异常体的边界,同时,垂直断层也可通过清晰的分界面进行识别,此外,垂直低阻断层也可视为与研究区纵向同等长度的低阻异常体,图 6和图 7低阻垂直断层的Ty实、虚部和幅值都表现出了与图 2低阻异常体相同的倾子响应形态,只是低阻垂直断层的倾子响应异常区整体往高频段偏移,而受两侧低(高)阻异常体的影响,低阻垂直断层Tx的倾子响应不够明显,但仍可通过两侧异常体的倾子响应形态大致圈出低阻垂直断层的边界,由此可知,组合模型每种资料响应在保留了单个异常体的响应形态的基础上整体反映了组合模型多个异常体之间相互作用的响应特征,通过异常区逐一分析可最终确定出组合模型的地电结构以及模型中每个异常体的边界.
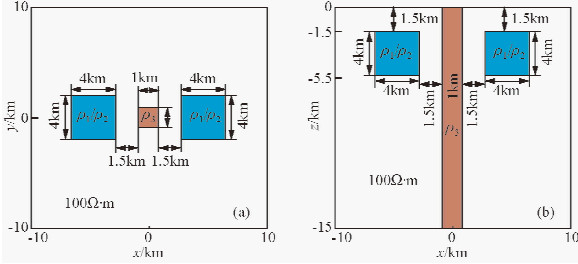 |
图 5 组合异常体模型示意图 (a)组合模型水平截面图;(b)组合模型垂直截面图. Fig. 5 Sketch of anomaly group bodies body model (a) Horizontal section diagram;(b) Vertical section diagram. |
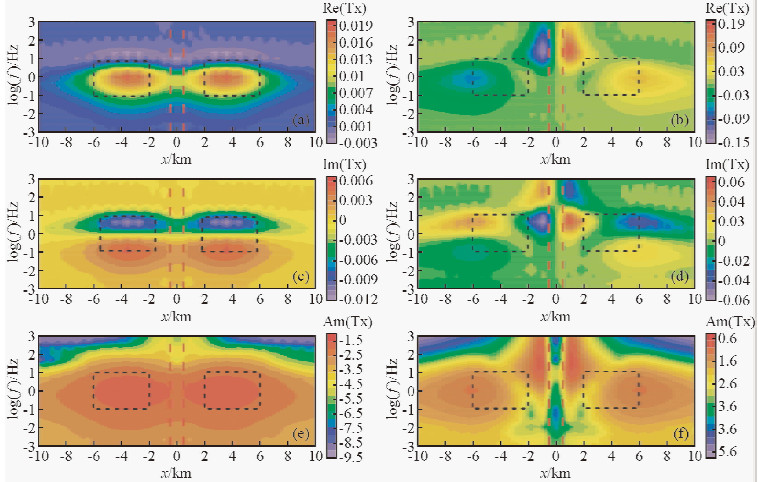 |
图 6 组合模型一三维倾子响应图 (a) Tx倾子实部;(b) Ty倾子实部;(c) Tx倾子虚部;(d) Ty倾子虚部;(e) Tx倾子幅值;(f) Ty倾子幅值. Fig. 6 3D response diagram for the first combination model (a) Re (Tx);(b) Re (Ty);(c) Im (Tx);(d) Im (Ty);(e) Am (Tx);(f) Am (Ty). |
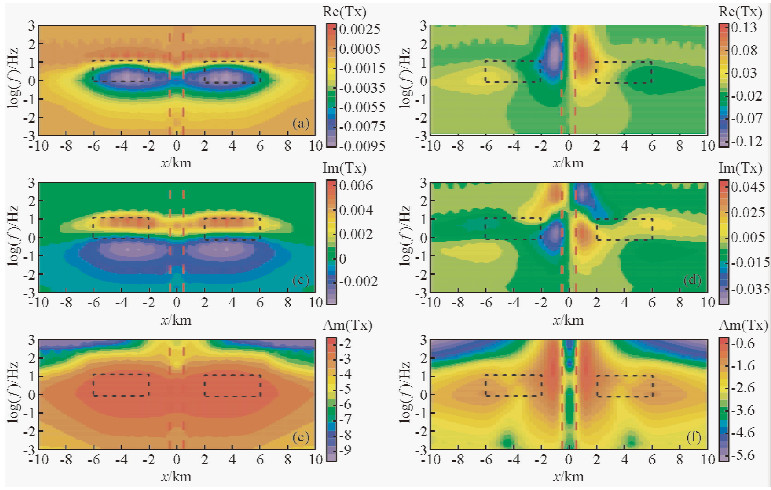 |
图 7 组合模型二三维倾子响应图 (a) Tx倾子实部;(b) Ty倾子实部;(c) Tx倾子虚部;(d) Ty倾子虚部;(e) Tx倾子幅值;(f) Ty倾子幅值. Fig. 7 3D response diagram for the second combination model (a) Re (Tx);(b) Re (Ty);(c) Im (Tx);(d) Im (Ty);(e) Am (Tx);(f) Am (Ty). |
本文在推导了利用有限差分和交错采样的方式离散化麦克斯韦方程组得到关于磁场的线性方程组的基础上进一步推导出倾子的计算公式,然后通过三维数值模拟方法开展三维条件下倾子响应特征的研究,并对几个典型地电模型的倾子响应特征进行模拟得出以下结论:
(1)倾子是大地电磁测深观测资料的一种有效的地电参数,具有对地下异常体良好的空间分辨率.
(2)作为大地电磁阻抗张量或视电阻率和相位资料的重要辅助数据,以倾子资料作为大地电磁测深法的一种解释手段,对提高大地电磁法解释精度具有重要意义.
致 谢 感谢审稿专家提出的宝贵修改意见和编辑部的大力支持!| [1] | Chen H, Deng J Z, Tan H D, et al. 2011. Study on divergence correction method in three-dimensional magnetotelluric modeling with staggered-grid finite difference method[J]. Chinese Journal Geophysics (in Chinese), 54(6): 1649-1659, doi: 10.3969/j.issn.0001-5733.2011.06.025. |
| [2] | Chen L S. 1989. The Magnetotelluric Sounding Data Processing and Interpretation Methods (in Chinese)[M]. Beijing: Petroleum Industry Press: 224-240. |
| [3] | Chen Q L, Hu W B, Li J M, et al. 2007. Characteristics of tipper response of buried sphere[J]. Journal of Oil and Gas Technology (in Chinese), 29(3): 75-78. |
| [4] | Chen X B, Zhao G Z, Ma X. 2006. Research on inversion of MT3D model approximately by 1D, 2D inversion method[J]. Chinese Journal of Engineering Geophysics (in Chinese), 3(1): 9-15. |
| [5] | Chen X B, Zhao G Z, Zhan Y, et al. 2004. Analysis of tipper visual vectors and its application[J]. Earth Science Frontiers (China University of Geosciences, Beijing) (in Chinese), 11(4): 626-636. |
| [6] | Chen X D, Zhao Y, Zhang J, et al. 2012. The applications of HTc SQUID magnetometer to TEM[J]. Chinese Journal of Geophysics (in Chinese), 55(2): 702-708, doi: 10.6038/j.issn.0001-5733.2012.02.034. |
| [7] | Ding H S, Sun J C, He Y S, et al. 2004. Research on non-destructive evaluation based on high Tc SQUID[J]. Journal of Test and Measurement Technology (in Chinese), 18(4): 311-315. |
| [8] | Farquharson C G, Olereberg D W, Haber E, et al. 2000. An algorithm for the three-dimensional inversion of magnetotelluric data[C].//72nd Ann. Int. Meeting Soc. Exploration Geophysics. Expanded Abstracts, 21, 649-652. |
| [9] | Gan J X. 2012. Finite element simulation and analysis of influence factors of MT tipper response (in Chinese)[D]. Changsha: Central South University. |
| [10] | Hu W B, Su Z L, Chen Q L, et al. 1997. Character of tipper data and the application[J]. Oil Geophysical Prospecting (in Chinese), 32(2): 202-213. |
| [11] | Witherly K, Sattel D. 2013. An assessment of 3D ZTEM results over three deposits[C].//23rd International Geophysical Conference and Exhibition, 11-14 August 2013-Melbourne, Australia. |
| [12] | Legault J. 2010. ZTEM Tipper AFMAG Results over the Morrison Copper/Gold Porphyry deposit[Z]. Geotech. Ltd.Case Study. |
| [13] | Lin C H, Tan H D, Tong T. 2011. Three-dimensional conjugate gradient inversion of tipper data[J]. Chinese Journal of Geophysics (in Chinese), 54(4): 1106-1113, doi: 10.3969/j.issn.0001-5733.2011.04.026. |
| [14] | Liu G D, Chen L S. 1993. Research on Magnetotelluric Sounding (in Chinese)[M]. Beijing: Geological Publishing House. |
| [15] | Liu J X, Gan J X, Tong X Z, et al. 2012. Finite element simulation and qualitative analysis of two-dimensional MT tipper response of tabular body[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 34(5): 541-547. |
| [16] | Ma P, Yang T, Xie F X, et al. 2001. The development and application of high Tc SQUID magnetometers[J]. Modern Instruments (in Chinese), (5): 28-30. |
| [17] | Pomposiello M C, Booker J R.,Favetto A. 2009. A discussion of bias in magnetotelluric responses[J]. Geophysics, 74(4): F59-F65. |
| [18] | Tan H D, Yu Q F, Booker J, et al. 2003. Magnetotelluric three-dimension modeling using the staggered-grid finite difference method[J]. Chinese Journal of Geophysics (in Chinese), 46(5): 705-711. |
| [19] | Tan H D, Wei W B, Deng M et al. 2004. General use formula in MT tensor impedance[J]. OGP (in Chinese), 39(1): 113-116. |
| [20] | Tong X Z, Liu J X, Liu Y, et al. 2011. Calculating tipper response in two-dimension magnetotelluric using finite element method[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 41(sup.1): 349-352. |
| [21] | Wu D. 2012. 2D & 3D tipper response and distinguishing to anomalous bodies (in Chinese)[D]. Changsha: Central South University. |
| [22] | Xi Z Z. 2013. Artificial source frequency-tipper sounding method (in Chinese)[D]. Changsha: Central South University. |
| [23] | Xu L H, Gan J X, Liu J X, et al. 2013. The analysis of influence factors of MT tipper response[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 35(4): 430-434. |
| [24] | Yu N. 2012. 2D/3D Tipper forward modeling and joint inversion of magnetotelluric (in Chinese)[D]. Chengdu: Chengdu University of Technology. |
| [25] | Yu N, Wang X B, Kan A K, et al. 2007. Study on tipper and apparent tipper and application in fault interpretation[J]. Chinese Journal of Engineering Geophysics (in Chinese), 4(4): 275-281. |
| [26] | 陈辉, 邓居智, 谭捍东,等. 2011. 大地电磁三维交错网格有限差分数值模拟中的散度校正方法研究[J]. 地球物理学报, 54(6): 1649-1659, doi: 10.3969/j.issn.0001-5733.2011.06.025. |
| [27] | 陈乐寿. 1989. 大地电磁测深资料处理与解释[M]. 北京: 石油工业出版社: 224-240. |
| [28] | 陈清礼, 胡文宝, 李金铭,等. 2007. 埋藏球体的倾子响应特征分析 [J]. 石油天然气学报, 29(3): 75-78. |
| [29] | 陈小斌, 赵国泽, 马霄. 2006. 大地电磁三维模型的一维二维反演近似问题研究[J]. 工程地球物理学报, 3(1): 9-15. |
| [30] | 陈小斌, 赵国泽, 詹艳,等. 2004. 磁倾子矢量的图示分析及其应用研究[J]. 地学前缘(中国地质大学, 北京), 11(4): 626-636. |
| [31] | 陈晓东, 赵毅, 张杰,等. 2012. 高温超导磁强计在瞬变电磁法中的应用研究[J]. 地球物理学报, 55(2): 702-708, doi: 10.6038/j.issn.0001-5733.2012.02.034. |
| [32] | 丁红胜, 孙景春, 何豫生,等. 2004. 高温超导量子干涉器在无损检测中的应用研究[J]. 测试技术学报, 18(4): 311-315. |
| [33] | 甘佳雄. 2012. MT倾子响应的有限元模拟及影响因素分析[D]. 长沙: 中南大学. |
| [34] | 胡文宝, 苏朱刘, 陈清礼,等. 1997. 倾子资料的特征及应用[J]. 石油地球物理勘探, 32(2): 202-213. |
| [35] | 林昌洪, 谭捍东, 佟拓. 2011. 倾子资料三维共轭梯度反演研究[J]. 地球物理学报, 54(4): 1106-1113, doi: 10.3969/j.issn.0001-5733.2011.04.026. |
| [36] | 刘国栋, 陈乐寿. 1993. 大地电磁测深研究[M]. 北京: 地质出版社. |
| [37] | 柳建新, 甘佳雄, 童孝忠,等. 2012. 板状体MT倾子响应的二维有限元模拟与定性分析[J]. 物探化探计算技术, 34(5): 541-547. |
| [38] | 马平, 杨涛, 谢飞翔,等. 2001. 高温超导量子干涉磁强计的发展现状及其应用[J]. 现代仪器, (5): 28-30. |
| [39] | 谭捍东, 余钦范, Booker J,等. 2003. 大地电磁法三维交错网格采样有限差分数值模拟[J]. 地球物理学报, 46(5): 705-711. |
| [40] | 谭捍东, 魏文博, 邓明,等. 2004. 大地电磁法张量阻抗通用计算公式[J]. 石油地球物理勘探, 39(1): 113-116. |
| [41] | 童孝忠, 柳建新, 刘颖,等. 2011. 利用有限单元法模拟二维MT倾子响应[J]. 吉林大学学报(地球科学版), 41(增刊1): 349-352. |
| [42] | 吴頔. 2012. 二维及三维倾子响应和异常体识别[D]. 长沙:中南大学. |
| [43] | 席振铢. 2013. 人工源频率倾子测深法[D]. 长沙: 中南大学. |
| [44] | 徐凌华, 甘佳雄, 柳建新,等. 2013. MT倾子响应的影响因素分析[J]. 物探化探计算技术, 35(4): 430-434. |
| [45] | 余年. 2012. 大地电磁二、三维倾子正演模拟与联合反演研究[D]. 成都: 成都理工大学. |
| [46] | 余年, 王绪本, 阚瑷珂,等. 2007. 倾子和视倾子的研究及在断裂解释中的应用[J]. 工程地球物理学报, 4(4): 275-281. |
 2015, Vol. 30
2015, Vol. 30


