地震层析成像是一种经典地球物理方法,其主要内容包括模型参数化、正演计算、成像反演等方面.其中,模型参数化是对地震波传播介质的定量化描述,它影响整个正演计算和反演过程,如射线追踪的速度和精度、数据信息的应用、反演策略以及重建模型的几何形态等(Zelt and Smith,1992; 郭飚,2003).模型参数化过程需要根据实际情况精心设置,不恰当的参数化方式会降低探测地球非均匀结构的能力(Thurber and Aki,1987).简化的模型可能使结构中有意义的信息被忽略,而过于复杂的模型可能会增强反演的不确定性,还有可能引入一些不真实的信息.目前,几个主流全球地震层析成像模型间差异的主要原因在于采用了不同的模型参数化方法(Chiao and Kuo,2001).因此,模型参数化是地震层析成像的关键基础步骤,是获得高质量成像结果的第一步.
层析成像中模型参数化过程是将介质参数投影到某一函数空间,并基于该空间的基函数进行展开(Nolet,2008).对于有限个观测di及误差ei,层析成像问题可以表示为



在实际地震走时层析成像研究中,层析成像的分辨能力主要依赖于射线密度及其方向的覆盖范围.一般来说,地震的震源和台站的不均匀分布是一个难以避免的因素,它会导致地震射线对模型空间采样不均匀.反演目标是尽可能地获得介质分布的细节信息,这意味着我们在参数化过程中应尽可能地细化网格,即尽量减小网格间距.但是,如果在分辨率不均匀的情况下(射线分布不均匀)采用均匀的网格划分就有可能在射线分布不好的区域过采样,造成虚假的结构信息.如果降低分辨率(即减小截断阶数)有可能损失数据中有效的信息并产生所谓的谱泄漏效应(Trampert and Snieder,1996).另外,从反问题的观点来看,反演问题变成混定问题,且是非常病态的方程,通常需要采用吉洪诺夫正则化(Tikhonov and Arsenin,1977).正则化函数的形式主要是基于对速度分布的光滑度的测量.目标函数的正则化可以压制非数据引起的速度结构振荡,并且可以显著地改善系统矩阵的条件数.但是正则化带来的问题是:1)光滑效应同时作用于模型的所有部分,而不考虑局部的解析能力.在数据分布较好分、辨率较高的区域也同样进行了光滑处理,而这正是地球物理学家所追逐的高分辨率地区.2)增加了计算量和对内存的需求.虽然Trampert and Snieder(1996)采用类似于加权阻尼因子的抗谱泄漏的反演算法,可以部分减少谱泄漏的影响,但Chiao and Liang(2003)指出,反演方程中的正则化项并非最小化模型参数m,而是最小化基函数的系数,也就是说,正则化过程并未尝试压制截断阶数以外模型的影响.
综上所述,模型参数化影响地震层析成像的多个方面,特别是数据非均匀采样和谱泄漏等问题必须在模型参数化过程中尝试解决.相对于正演走时计算和反演算法,模型参数化方法对成像结果的影响研究还不够,目前关于模型参数化方法的对比分析、对层析成像结果的影响以及研究进展的相关讨论还非常鲜见.本文拟回顾20世纪70年代以来地震层析成像研究中所涉及的模型参数化方法,并根据其分辨率模式对参数化方法进行分类,探讨不同模型参数化方法的优缺点以及对地震层析成像结果的影响(包括结果的分辨率和可靠性),希望本文能够抛砖引玉,进一步推进学术界对层析成像中的参数化方法的研究.
1 单尺度模型参数化单一尺度模型参数化方法是指参数化节点位置固定,模型分辨率不变的方法,如常速度块、离散节点、非均匀网格等方法.
1.1 常速度块参数化方法常速度块参数化方法将研究区域的介质分成多个常速度块,以体现速度的横向和纵向变化.在笛卡尔坐标系下将整个反演模型用多个均匀的六面体(图 1a)表示,用每个六面体中心的速度来表示该六面体的整体速度,这种参数化方法称之为常速度块方法(Constant Block).Aki and Lee(1976)最早采用该方法进行层析成像研究.Inoue等(1990)在全球尺度上使用等角度的经纬度的规则网格,径向上每层的厚度是随深度变化的(图 1b). van der Hilst等(1997)应用常速度块模型对地幔对流进行了研究.
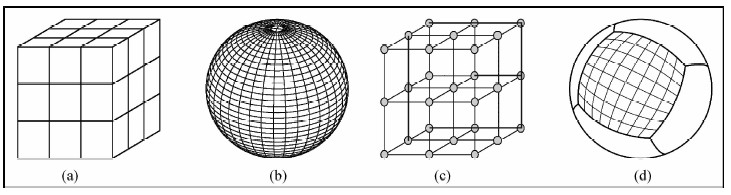 | 图 1 单一尺度参数化模型
(a)常速度块模型(Rawlinson and Sambridge,2003);(b)根据经纬度划分的模型(Ballard et al.,2009);(c)速度节点模型(Rawlinson and Sambridge,2003);(d)立方球模型(Simons et al.,2011).Fig. 1 Single-scale parameterization model (a)Constant velocity blocks model(Rawlinson and Sambridge,2003);(b)Regularly spaced latitude-longitude blocks model(Ballard et al.,2009);(c)A grid of velocity nodes model(Rawlinson and Sambridge,2003);(d)Chunks model(Simons et al.,2011). |
由于相邻速度块之间速度不连续,会产生人为的速度间断,这些速度间断会造成射线影区及射线的交叉(Rawlinson and Sambridge,2003).在球坐标系下,该方法存在一个很重要的问题:依据经纬度网格对模型进行划分会造成高纬度地区网格比赤道地区网格小,并且在两极存在奇异点.刘福田等(1989)指出,在进行正演时,通常假定为常速度块,而在反演结果的解释中,通常要对各块的数值进行插值,这意味着各块的速度不再是常数.这种常速度块的假定与反演结果解释时非常速度块体的假定不协调.常速度块方法不适合用于表示复杂介质,目前在近震层析成像和人工地震勘探领域应用较少.但基于方法简单、易定义、射线路径和走时容易计算的特点,目前主要用于大尺度的层析成像研究中,如远震层析成像(Aki et al.,1977; Oncescu et al.,1984; Humphreys and Clayton,1988,1990; Benz et al.,1992; Achauer,1994; Saltzer and Humphreys,1997)和全球层析成像(Grand et al.,1997; Vasco and Johnson,1998; van der Hilst et al.,1997; Boschi and Dziewonski,1999).与常速度块类似的方法还有常速度梯度方法,即三角网格(三维情况下为四面体)(Chapman and Drummond,1982; White,1989).
1.2 离散节点参数化方法离散网格点模型参数化是通过定义离散节点的位置、节点上的参数值和插值函数来描述介质模型.模型中任意一点的参数值可以通过节点上的值和插值函数获得.Thurber(1983)首次在近震层析成像中应用网格点速度模型参数化方法(图 1c).该方法采用矩形节点设置,在模型内任意一点的速度值可以用周围八个顶点速度值表示.其采用的插值函数为三维线性插值函数:
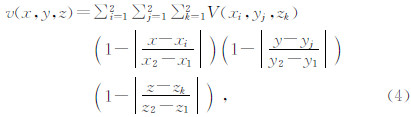
由于某些射线追踪方法(如高阶有限差分方法)需要用到速度场的一阶和二阶连续导数.因此须采用高阶插值函数.Thomson and Gubbins(1982)和Sambridge(1990)分别在远震和近震层析成像研究中采用基样条插值函数.虽然用越高阶的插值函数,模型就越平滑,但是这需要更多的基函数,如三维线性插值需要8个顶点定义一阶连续单元,而三次B样条需要64个顶点定义出二阶连续单元.三次B样条插值方法是较为常用的高阶插值方法.这种方法的优点在于:1)具有局部支撑和局部修改特性,避免了基样条全局影响的缺点(Shalev,1993);2)一般不需要在反演的目标函数中加入额外的光滑项(Rawlinson and Sambridge,2003).Lutter and Nowack(1990),Farra and Madariaga(1988),McCaughey and Singh(1997),Rawlinson and Sambridge(2003)采用三次B样条插值函数进行参数化.郭飚等(2009)采用非均匀有理B样条(NURBS)插值函数进行了远震层析成像研究,NURBS插值可以赋予每个节点以不同的权值,并且在实际层析成像应用中可以根据每个节点上射线数来定权值的大小,从而部分克服射线非均匀采样的影响.
在全球尺度层析成像中,根据经纬度设置的规则的速度块或节点参数化方式会在高纬度地区扭曲变形.为了解决这个问题,Wang and Dahlen(1995)和Wang等(1998)发展了球面三角网格样条函数,Ronchi等(1996)在全球波形层析成像研究中引入了立方球参数化模型(Chunks模型,见图 1d).
1.3 非均匀网格参数化上述的模型参数化方法对模型的划分大小都是固定的,进而模型的分辨率也是固定的.鉴于地震台站、震源分布以及射线弯曲等因素,大多数走时层析成像研究的射线在模型内部分布极不均匀,常用的规则网格参数化方法无法自适应非均匀采样的数据,因此需要引入不规则网格参数化(Sambridge et al.,1995).
非均匀网格参数化的目标是根据数据对模型空间采样的密度或研究目标来非均匀划分反演网格的大小,即在射线较为稀疏的区域采用粗糙的网格,在射线密集的区域采用较为精细的网格.采用非均匀网格可以最大程度提取数据中的结构信息,同时可以减少未知数的数量,降低反演方程的条件数.非均匀网格技术可以大致分为两类:一类是基于规则的网格,并通过网格的合并、分解等算法构造非均匀网格.另一类基于Delaunay算法(或Voronoi(Voronoi,1907))来构造非均匀的三角网格或四面体网格.
Abers and Roecker(1991)将研究区域划分为小尺度均匀三维速度块,然后根据射线分布将小尺度的速度块合成为更大的不规则多面体,从而构成不规则的反演单元.该方法需要人为控制参数化过程,难以在大尺度研究中应用.Vesnaver(1996)根据真实数据在模型空间的分辨能力,采用相邻块合并、改变块体边界及将一个块分裂为多个块的方法构造不规则网格.该方法利用模型偏导数矩阵SVD分解计算零空间能量来测量数据的空间分辨能力.当研究尺度较大时,该方法计算零空间能量的过程非常耗时.Bijwaard等(1998)采用类似的思路在全球尺度上构造了完全自动的算法,该算法在全球层析成像研究中得到了广泛应用(Bijwaard and Spakman,2000; Spakman and Bijwaard,2001; Li et al.,2008).Grunberg and Genaud(2004)给出了相应的并行算法.
四面体网格是一种常用的非结构网格.它具有简单、易于生成等特点,在计算力学、计算机图形学等领域获得了广泛应用.四面体是多面体中最简单的形式,不同于其它的多面体,四面体完全由四个顶点定义,不存在奇异和多解.在二维情况下,四面体网格退化为三角网格.Sambridge等(1995)利用Delaunay方法构建了四面体参数化网格,并在区域内使用自然邻近差值法使整个区域光滑.Faletič (1997)首先用二十面体描述整个地球,然后根据射线密度和上一次迭代的速度模型的梯度进一步细分每一个四面体(图 2a).该方法解决了常规经纬网格在两极的扭曲和奇异的问题.Ballard等(2009)采用了类似的参数化方法并详细的讨论了该模型框架下走时计算问题,Sambridge and Gudmundson(1998)及Sambridge and Faletič(2003)就此进一步改进了该算法.Vesnaver and BÖhm(2000),BÖhm等(2000)及Trinks等(2005)将类似的非均匀三角网格参数化方法应用于反射层析成像中.Zhang and Thurber(2005)在近震层析成像研究中发展了基于数据分布的自适应网格参数化方法,该方法采用Quickhull算法(Barber et al.,1993)来构建非均匀四面体网格(图 2b).基于Delaunay三角形和Voronoi多边形的非均匀网格技术具有以下特点:1)可以根据数据分布和反演目标灵活设置非均匀节点;2)相应算法(数据结构、索引、网格加密等)成熟;3)可以在反演过程中动态调整节点的设置;4)可以得到最少的钝角三角形的解.但当初始条件设置不合理或数据分布极度非均匀时,该算法可能会给出不合理的网格划分甚至失效.
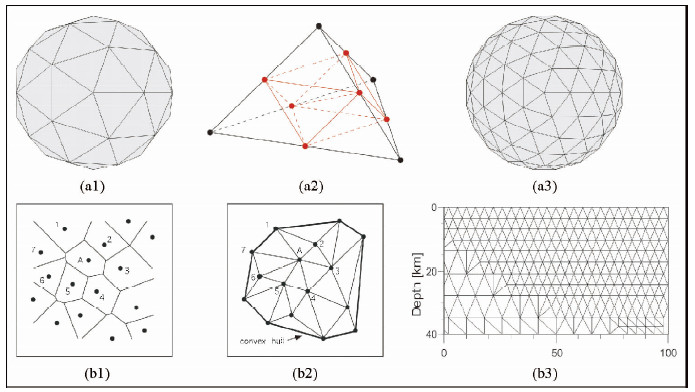 | 图 2 非均匀网格参数化模型
(a1)球面二十面体(Sambridge and Faletič,2003);(a2)四面体细分示意图(Sambridge and Faletič;,2003);(a3)球面二十面体一次细分图(Sambridge and Faletič,2003);(b1)泰森多边形(Sambridge et al.,1995);(b2)德劳内三角形(Sambridge et al.,1995);(b3)自适应三角形划分网格(Trinks et al.,2005,modified).Fig. 2 Non-uniform grid parameterization model (a1)An icosahedrons(Sambridge and Faletič,2003);(a2)Bi-section of a tetrahedron(Sambridge and Faletič,2003);(a3)A subdivision of an icosahedrons(Sambridge and Faletič,2003);(b1)Voronoi cells(Sambridge et al.,1995);(b2)Delaunay Triangulations(Sambridge et al.,1995);(b3)Adaptive triangulations grid(Trinks et al.,2005,modified). |
多尺度参数化方法是指模型参数包含不同尺度(或分辨率、波长)的信息,最终的结果是不同尺度信息的叠加.虽然非均匀网格技术可以使研究区域内不同位置具有不同的分辨率,但同一位置还是单一分辨率的.Zhou(1996,2003)将之前传统的不重叠的块方法称为单尺度参数化(SST),在此基础上提出了多尺度参数化概念(MST).首先定义许多不同尺度大小的子模型,每个子模型都覆盖全模型区域.然后,将全部子模型同时反演.最后得到的模型是所有子模型值叠加的结果.实际上,他所提出的MST就是许多不同分辨率的SST结果的叠加.该方法能够自适应射线的非均匀分布并能给出不同尺度上的结构.该方法仅仅是将空间域不同尺度的结构简单叠加,没有考虑空间分辨率与频率分辨率的关系,在理论上并不完备.另外,上述方法都是空间域参数化方法,空间域方法的优点是简便直观、易于构造,但难以客观的设定速度块的大小(或网格间距).由于其没有考虑谱域的分辨能力,在所得到的解中不可避免地混入了人为因素造成的虚假结构,这在采用过参数化(即将研究区域分成非常多细小的块体)时尤为严重.究其原因主要在于射线对模型的取样是空间非均匀的,因此在空间域均匀离散的参数化方法是不太合适的(朱露培等,1990).
2.1 谱域参数化方法谱域参数化是将模型参数在频率波数域离散化,一般应用球谐函数在全球尺度上展开或用截断傅里叶级数在区域尺度上展开.Dziewonski等(1977)最先应用球谐函数参数化方法获得了全球地幔长周期速度结构.通过设定展开阶数可以获得任意精度的速度模型,并且在描绘长周期尺度的结构变化时仅需较少的参数即可获得稳定的解.利用该方法得到的结构便于直接与大地测量、热流、重力及磁场数据进行对比(都是基于球谐函数表示).该方法是采用全局尺度的基函数,因此局部误差会影响到(或泄露)其他区域.另外,当分辨率较高时需要的参数会急剧增加(Nolet,2008).例如,要得到水平分辨率为100 km的结构,球谐函数项N=200时,总共需要80000个球谐基函数项.因此在决定球谐函数项数N时要结合所需解决问题的需求和反演中计算量大小、可实行程度等技术问题.Kuo等(2000)曾采用混合的参数化方法,首先采用球谐函数获得低频结构,然后采用局域尺度基函数的参数化方法获得高分辨率的区域结构.球谐函数参数化方法在全球层析成像中获得了广泛应用(Dziewonski et al.,1977; Dziewonski and Woodhouse,1987; Li et al.,1991; Trampert and Woodhouse,1995; Reid et al.,2001; Romanowicz and Gung,2002).
朱露培等(1990)提出了基于傅里叶级数的参数化法,将待求扰动场按空间频率展开,以便反演各阶频率系数.慢度场可用截断的傅里叶级数表示为
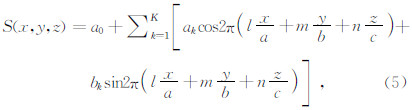
傅里叶变换的基函数是在两个方向上都无限伸展的正弦曲线,具有全域支撑特性,不适于处理有明显局域特征的非平稳信号.虽然通过加窗的傅里叶变换(短时傅里叶变换)能够提供信号在某个时间段或某个频率范围的信息,但其缺点是对所有的频率成分,其时间窗的大小都相同.
小波变换继承和发展了短时傅立叶变换局部化的思想,同时又克服了窗口大小不随频率变化的缺点.它能够提供一个随频率改变的“时间—频率”窗口,是进行信号时频分析和处理的理想工具.小波变换的中心频率与带宽比是恒定的.与Fourier变换相比,小波变换是时间(空间)频率的局部化分析,通过伸缩平移运算,它对信号(函数)逐步进行多尺度分析,最终达到在高频处时间细分,低频处频率细分,能自动适应时频信号分析的要求,从而可聚焦到信号的任意细节(Daubechies,1992).小波分析因其具有自适应性和多尺度分析特性,小波分析能够突出信号某些方面的特征,在数据压缩、去噪、图像识别、医学成像等领域获得了广泛应用.
Bhatia等(1994)将小波变换技术应用于医学成像,Li等(1996)首次将小波变换方法应用于一维地球物理反演问题的模型构建.Chiao and Kuo(2001)采用二代小波技术构建了二维球面小波变换,并系统地阐述了小波域参数化方法.具体方法是先在球面上建立一个二十面体,再根据分解阶数将每个球面三角形继续细分成四个子三角形,进而构建了多尺度分析序列.该方法基于球面块方法,能充分反映采样密度,即在射线密度高、交叉路径多的区域网格间隔密集;相反,射线密度低、交叉路径少的区域网格间隔稀疏.稀疏区间显示长波特征(低波数),有更好的谱域分辨率;密集区间显示短波特征(高波数),有更好的空间分辨率.
自Chiao and Kuo(2001)采用小波变换以来,人们逐渐认识到小波域参数化的优点,基于小波变换的多尺度参数化技术成为目前层析成像技术发展的前沿.Chiao and Liang(2003)在笛卡尔坐标系下利用样条小波函数构建三维小波域参数化方法,并通过合成数据测试对比了小波域与空间域参数化方法.数值试验表明,采用小波域参数化技术可以同时获得多个尺度的结构信息,特别是在数据采样不均匀的情况下,图像的恢复情况远远好于空间域参数化方法.Tikhotsky and Achauer(2008)在笛卡尔坐标系下,利用Harr小波构建了用于可控制源的层析成像模型参数化方法.该方法通过张量积的形式构造了三维Haar小波变换,并基于射线密度和方位覆盖率两个参数来约束反演.Hung等(2010,2011)利用小波域参数化方法研究了青藏南缘上地幔速度结构.Chevrot and Zhao(2007)构造了三维Harr小波参数化方法并进行区域尺度的面波层析成像研究.Loris等(2007)采用L1范数正则化技术构建小波域层析成像反演的目标函数,大大地改善了解的稳定性.Simons等(2011)应用立方球体变换(即笛卡尔坐标系到球坐标系的映射),将地球映射为六个拼接在一起的块体(Superchunks),然后在新坐标系下构建小波域的参数化.Fang and Zhang(2014)构造了基于小波变换和L1范数稀疏反演的双差层析成像方法.
在小波域进行层析成像的模型参数化有以下优点:1)小波基是局部支撑的,因此小波分解方法能有效地表示模型中不同尺度的非均匀变化并且避免受其它区域结构的影响.该特性特别适合处理非均匀采样数据的反演.例如,射线覆盖较差的区域高阶小波系数较小(或为零),反演过程自动处理该区的低阶小波系数(即低分辨率结构)(见图 3c);2)小波域参数化同时包含不同尺度的结构信息(即模型中既包含了大尺度平均速度信息,也包含小尺度高频变化的信息);3)小波变换是稀疏变换,在基于有限分辨率表示情况下,可以大大减少参数的个数.另外,基于小波变换的稀疏特性采用相应的基于稀疏约束的反演方法可以有效的降低反问题的多解性.
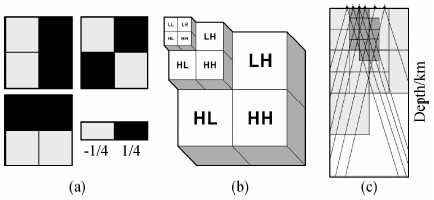 | 图 3 小波域参数化模型
(a)二维haar小波函数示意图(Tikhotsky and Achauer,2008);(b)多尺度三维小波分解示意图;(c)多尺度小波参数化横截面示意图,斜线表示射线(Hung et al.,2011).Fig. 3 Wavelet parameterization model (a)A sketch of the 2D Haar wavelet ‘mother’ function(Tikhotsky and Achauer,2008);(b)A sketch of 3D multi-scale wavelet decomposition;(c)A schematic cross section multi-scale wavelet parameterization. Slant lines represent raypaths(solid triangles)(Hung et al.,2011). |
目前可以通过张量积的方法构造高维小波,但这样构建的小波方向分辨率很差.球面上的小波变换的相关理论和方法仍需进一步发展,自适应小波域参数化方法也有待于发展和完善.
3 分区参数化及多重网格上述介绍的模型参数化方法大多数是描述连续变化的 速度场,而实际地球介质存在不同尺度的速度间断面,如Moho面、断层带等,这些速度间断面将介质分为多个不连续区域.另外,地震层析成像研究中有时需要计算折射波或反射波等后续震相,这要求速度模型中包含速度间断面.
界面参数化与速度参数化类似,本质都是用一种数学表达式来代表地质结构,以适用于正、反演过程.Chiu等(1986)在反射层析成像中加入了不连续面Moho面.Zelt and Smith(1992)和Williamson(1990)分别在广角方法、反射方法中使用了二维分段线性的几何图形作为速度界面,其缺点是在两段之间的连接点处界面的梯度不连续,这种不连续在地质上是不真实的,会产生人工影区.Sambridge(1990)和Guiziou等(1996)在反射走时地震层析成像研究中采用三维分段的三角形区域代表分界面.用三角形划分的优点是很容易描述一个多值的平面,但是该分段线性方法中分段联接点处的界面梯度是不连续的.White(1989),Lutter and Nowack(1990)和Rawlinson and Houseman(1998)使用传统三次样条函数构造二维界面,可使界面二阶连续.Chiu等(1986)在反射层析成像方法中用n阶多项式描述界面.Wang and Houseman(1994)用截断傅里叶系数描述界面,通过截断阶数控制着界面的光滑性.
引入速度间断面的优点在于可以考虑先验的地质特征,如断层、褶皱或地球内部主要的间断面(如Moho界面和Conrad界面等).速度间断面的起伏会引起走时的变化,在研究精细结构时应把这种波动考虑进去.刘福田等(1989)、Zhao等(1992,1994)在研究中引入了速度间断面,速度间断面的位置在反演中固定不变.Rawlinson and Sambridge(2005)在反射层析成像研究中同时反演了速度结构和间断面的起伏.
对于非线性较强的反问题,选择尽量接近真实介质的初始模型无疑有助于我们得到逼近真实的解.地震层析成像的初始模型应尽量引入已有的先验信息,如速度结构、间断面位置及沉积层厚度等,而这些先验信息的分辨率一般与层析成像研究的目标分辨率并不一致.走时场及射线路径的计算需要较为精细的速度结构,以便考虑先验信息(如沉积层厚度、断层位置以及其它的研究结果等).但是反演节点的设置需要考虑数据的分辨能力,以及数据的非均匀分布,因此反演网格一般采用相对粗糙的非均匀分布网格节点.Kissling等(2001)提出了三重网格参数化思想,即在正演、反演及解释过程中采用三个不同的参数网格:正演计算和射线追踪采用细化的规则“数值”网格;反演过程采用粗糙非均匀的“反演”网格,其单元大小可以确保在大部分地区有一致的合理的分辨率;解释过程采用相对粗化的“地震”网格,其单元大小足以代表该处先验速度结构中已知的最小的构造.三重网格方法可以减少不同正、反演算法对最后的速度模型结果的影响,以便更好利用正、反演算法的特点,充分利用已知的地球先验信息和数据的分辨能力.
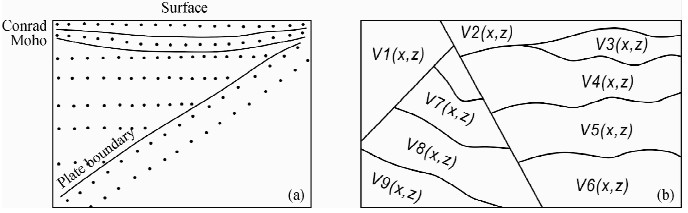 | 图 4 分区参数化模型
(a)简单速度间断面(Zhao et al.,1992);(b)复杂速度间断面(Rawlinson et al.,2010).Fig. 4 A schematic representation of layered parameterization model (a)Simple velocity discontinuities(SVDs)(Zhao et al.,1992);(b)Flexible velocity discontinuities(Rawlinson et al.,2010). |
4.1 模型参数化与层析成像的正反演过程紧密相连,不同的参数化方法应采用与之相适应的正反演方法.例如,采用空间域过参数化方法,需要匹配相应较大的阻尼参数;采用稀疏小波域的参数化,则L1或L0范数的正则化可能是较优的选择.
4.2 参数化方法的选择应根据研究区域的大小、研究目标、数据的类型、数据的质量以及计算能力等条件进行选择.例如,在研究全球尺度地幔结构时,球谐函数的参数化方法可以有效地减少计算量、提高反演的稳定性,但在研究区域尺度结构时,该方法就不适用.恰当地选择参数化方法将使我们能最大限度地从观测数据中提取正确的信息.反之,有可能导致遗失有用的信息,甚至得到错误的结果.
4.3 不同类型的地球物理观测数据及物理参数的联合反演能够降低地球物理解的非唯一性、相互约束,并给出较为严格的地球物理模型.因此,实施多种地球物理方法的联合反演是地球物理探测研究的趋势.由于不同的数据类型及不同的地球物理方法具有不同的分辨率,观测数据对模型的采样也将不同.因此,多尺度参数化方法有利于在同一参数化模型框架下实现联合反演.
4.4 国内学者在地震层析成像的模型参数化研究中也取得了很多重要进展.刘福田等(1989)较早提出在模型参数化中引入了速度间断面,该方法在国内层析成像研究中广泛应用(刘建华等,1996;胥颐等,2006,2013).朱露培等(1990)最早提出了采用傅里叶级数构建速度模型,该方法是多尺度参数化方法的雏形.郭飚等(2009)首次利用非均匀有理B样条进行了模型参数化.
4.5 研究能自适应数据的分布情况、抗谱泄漏效应,并且能同时考虑空间域及频率域分辨率是参数化的重要目标.空间域参数化方法需要较多的人为控制(节点的间距及反演的阻尼因子等),会在所得到的解中混入人为的虚假结构,以至于反演的解发生畸变.而频率域参数化方法可以根据Frechet导数在不同尺度上的分解相对自动地调节扰动的分配,有效地减少人为因素,特别是稀疏表示的小波域参数化方法能适应不同数据分布,不同分辨率要求.因此,小波域多尺度稀疏表示的参数化方法是未来参数化发展的方向.
致 谢 感谢审稿专家提出的宝贵修改意见和编辑部的大力支持!| [1] | Abers G A, Roecker S W. 1991. Deep structure of an arc-continent collision: earthquake relocation and inversion for upper mantle P and S-wave velocities beneath Papua New Guinea[J]. Journal of Geophysical Research, 96(B4): 6379-6401. |
| [2] | Achauer U. 1994. New ideas on the Kenya rift based on the inversion of the combined dataset of the 1985 and 1989/90 seismic tomography experiments[J]. Tectonophysics, 236(1-4): 305-329. |
| [3] | Aki K, Christofferson A, Husebye E S. 1977. Determination of the three-dimensional seismic structure of the lithosphere[J]. Journal of Geophysical Research, 82(2): 277-296. |
| [4] | Aki K, Lee W H K. 1976. Determination of three-dimensional velocity anomalies under a seismic array using first P arrival times from local earthquakes: 1. A homogeneous initial model[J]. Journal of Geophysical Research, 81(23): 4381-4399. |
| [5] | Ballard S, Hipp J R, Young C J. 2009. Efficient and accurate calculation of ray theory seismic travel time through variable resolution 3D earth models[J]. Seismological Research Letters, 80(6): 989-999, doi: 10.1785/gssrl.80.6.990. |
| [6] | Barber C B, Dobkin D P, Huhdanpaa H. 1993. The quickhull algorithm for convex hull[R]. Tech. Rep. GCG53, The Geometry Cent., Univ. of Minnesota, Minn. |
| [7] | Benz H M, Zandt G, Oppenheimer D H. 1992. Lithospheric structure of northern California from teleseismic images of the upper mantle[J]. Journal of Geophysical Research, 97(B4): 4791-4807. |
| [8] | Bhatia M, Karl W C, Willsky A S. 1994. A wavelet-based method for multiscale tomographic reconstruction[R]. MIT Tech Rep. LIDS-P-2182. |
| [9] | Bijwaard H, Spakman W, Engdahl E R. 1998. Closing the gap between regional and global travel time tomography[J]. Journal of Geophysical Research, 103(B12): 30055-30078. |
| [10] | Bijwaard H, Spakman W. 2000. Nonlinear global P-wave tomography by iterated linearized inversion[J]. Geophys. J. Int., 141(1): 71-82. |
| [11] | BÖhm G, Galuppo P, Vesnaver A. 2000. 3D adaptive tomography using Delaunay triangles and Voronoi polygons[J]. Geophys. Prospect., 48(4): 723-744. |
| [12] | Boschi L, Dziewonski A M. 1999. High- and low-resolution images of the Earth’s mantle-implications of different approaches to tomographic modeling[J]. Journal of Geophysical Research, 104(B11): 25567-25594. |
| [13] | Cao L M, Xu Y, Wu S G. 2013. Finite difference tomography of the crustal velocity structure in Tengchong, Yunnan province[J]. Chinese Journal Geophysics (in Chinese), 56(4): 1159-1167, doi: 10.6038/cjg20130411. |
| [14] | Chapman C H, Drummond R. 1982. Body-wave seismograms in inhomogeneous media using Maslov asymptotic theory[J]. Bull. Seismol. Soc. Am., 72(6B): S277-S317. |
| [15] | Chevrot S, Zhao L. 2007. Multiscale finite-frequency Rayleigh wave tomography of the Kaapvaal craton[J]. Geophys. J. Int., 169(1): 201-215. |
| [16] | Chiao L Y, Kuo B Y. 2001. Multiscale seismic tomography[J]. Geophys. J. Int., 145(2): 517-527. |
| [17] | Chiao L Y, Liang W Z. 2003. Multiresolution parameterization for geophysical inverse problems[J]. Geophysics, 68(1): 199-209. |
| [18] | Chiu S K L, Kanasewich E R, Phadke S. 1986. Three-dimensional determination of structure and velocity by seismic tomography[J]. Geophysics, 51(8): 1559-1571. |
| [19] | Daubechies I. 1992. Ten Lectures on Wavelets[M]. American: Society for Industrial and Applied Mathematics. |
| [20] | Dziewonski A M, Hager B H, O’Connel T J. 1977. Large-scale heterogeneities in the lower mantle[J]. Journal of Geophysical Research, 82(2): 239-255. |
| [21] | Dziewonski A M, Woodhouse J H. 1987. Global images of the Earth’s interior[J]. Science, 236(4797): 37-48. |
| [22] | Eberhart-Phillips D. 1986. Three-dimensional velocity structure in northern California coast ranges from inversion of local earthquake arrival times[J]. Bull. Seismol. Soc. Am., 76(4): 1025-1052. |
| [23] | Eberhart-Phillips D, Labson V F, Stanley W D, et al. 1990a. Preliminary Velocity and Resistivity Models of the Loma Prieta Earthquake Region[J]. Geophys. Res. Lett., 17(8): 1235-1238. |
| [24] | Eberhart-Phillips D. 1990b. Three-dimensional P and S velocity structure in the Coalinga Region, California[J]. Journal of Geophysical Research, 95(B10): 15343-15363. |
| [25] | Eberhart-Phillips D, Michael A J. 1993. Three-dimensional velocity structure, seismicity, and fault structure in the Parkfield Region, central CA[J]. Journal of Geophysical Research, 98(B9): 15737-15758. |
| [26] | Faletič R. 1997. Seismic Tomography with a self-adaptive parameterisation[D]. Canberra: Australian National University. |
| [27] | Fan J K, Wu S G. 2014. P-wave seismic tomography of the Manila subduction zone[J]. Chinese Journal Geophysics (in Chinese), 57(7): 2127-2137, doi: 10.6038/cjg20140709. |
| [28] | Fang H, Zhang H. 2014. Wavelet-based double-difference seismic tomography with sparsity Regularization[J]. Geophys. J. Int., 199(2): 944-955, doi: 10.1093/gji/ggu305. |
| [29] | Farra V, Madariaga R. 1988. Non-linear reflection tomography[J]. Geophys. J. Int., 95(1): 135-147. |
| [30] | Grand S P, van der Hilst R D, Widiyantoro S. 1997. Global seismic tomography: a snapshot of convection in the Earth[J]. GSA Today, 7: 1-7. |
| [31] | Grunberg M, Genaud S. 2004. Parallel adaptive mesh coarsening for seismic tomography[C]//16th Symposium on Computer Architecture and High Performance Computing. Foz do Iguacu, PR, Brazil: IEEE, 158-165. |
| [32] | Guiziou J L, Mallet J L, Madariaga R. 1996. 3-D seismic reflection tomography on top of the GOCAD depth modeler[J]. Geophysics, 61(5): 1499-1510. |
| [33] | Guo B. 2003. Portable Broadband Seismic Array Obseration: Earthquakes Location and Seismic Tomography (in Chinese)[D]. Beijing: Institute of Geology, China Earthquake Administration. |
| [34] | Guo B, Liu Q Y, Chen J H, et al. 2009. Teleseismic P-wave tomography of the crust and upper mantle in Longmenshan area, west Sichuan[J]. Chinese Journal of Geophysics (in Chinese), 52(2): 346-355. |
| [35] | Hammer P T C, Dorman L M, Hildebrand J A, et al. 1994. Jasper Seamount structure: Seafloor seismic refraction tomography[J]. J. Geophys. Res., 99(B4): 6731-6752. |
| [36] | Haslinger F, Kissling E, Ansorge J, et al. 1999. 3D crustal structure from local earthquake tomography around the Gulf of Arta (Ionian region, NW Greece) [J]. Tectonophysics, 304(3): 201-218. |
| [37] | Hildebrand J A, Dorman L M, Hammer P T C, et al. 1989. Seismic tomography of Jasper Seamount[J]. Geophys. Res. Lett., 16(12): 1355-1358. |
| [38] | Humphreys E D, Clayton R W. 1988. Adaption of back projection tomography to seismic travel time problems[J]. Journal of Geophysical Research, 93(B2): 1073-1085. |
| [39] | Humphreys E D, Clayton R W. 1990. Tomographic image of the Southern California Mantle[J]. Journal of Geophysical Research, 95(B12): 19725-19746. |
| [40] | Hung S H, Chen W P, Chiao L Y, et al. 2010. First multi-scale, finite-frequency tomography illuminates 3-D anatomy of the Tibetan Plateau[J]. Geophys. Res. Lett., 37: L06304, doi: 10.1029/2009GL041875. |
| [41] | Hung S H, Chen W P, Chiao L Y, et al. 2011. A data-adaptive, multiscale approach of finite-frequency, traveltime tomography with special reference to P and S wave data from central Tibet[J]. Journal of Geophysical Research, 116: B06307, doi: 10.1029/2010JB 008190. |
| [42] | Inoue H, Fukao Y, Tanabe K, et al. 1990. Whole mantle P-wave travel time tomography[J]. Phys. Earth Planet. Inter., 59(4): 294-328. |
| [43] | Kissling E, Husen S, Haslinger F. 2001. Model parametrization in seismic tomography: a choice of consequence for the solution quality[J]. Physics of the Earth and Planetary Interior, 123(2-4): 89-101. |
| [44] | Kuo B Y, Garnero E J, Lay T. 2000. Tomographic inversion of S-SKS times for shear velocity heterogeneity in D'': Degree 12 and hybrid models[J]. J. Geophys. Res., 105(B12): 28139-28158. |
| [45] | Li C, van der Hilst R D, Meltzer A S, et al. 2008. Subduction of the Indian lithosphere beneath the Tibetan Plateau and Burma[J]. Earth and Planetary Science Letters, 274(1-2): 157-168. |
| [46] | Li X D, Giardini D, Woodhouse J H. 1991. Large-scale three-dimensional even-degree structure of the earth from splitting of long-period normal modes[J]. Journal of Geophysical Research, 96(B1): 551-577. |
| [47] | Li X G, Sacchi M D, Ulrych T J. 1996. Wavelet transform inversion with prior scale information[J]. Geophysics, 61(5): 1379-1385. |
| [48] | Liu F T, Li Q, Wu H, et al. 1989. On the tomographic inverse method used in velocity image reconstruction[J]. Acta Geophysica Sinica (in Chinese), 32(1): 46-61. |
| [49] | Liu J H, Wu H, Liu F T. 1996. Features of 3-D velocity distribution and lithosphere structure in South China and its contiguous sea area[J]. Acta Geophysica Sinica (in Chinese), 39(4): 483-492. |
| [50] | Loris I, Nolet G, Daubechies I, et al. 2007. Tomographic inversion using l1-norm regularization of wavelet coefficients[J]. Geophys. J. Int., 170(1): 359-370. |
| [51] | Lutter W J, Nowack R L. 1990. Inversion for crustal structure using reflections from the PASSCAL Ouachita experiment[J]. Journal of Geophysical Research, 95(B4): 4633-4646. |
| [52] | McCaughey M, Singh S C. 1997. Simultaneous velocity and interface tomography of normal-incidence and wide-aperture seismic traveltime data[J]. Geophys. J. Int., 131(1): 87-99. |
| [53] | Nolet G. 2008. A Breviary of Seismic Tomography: Imaging the Interior of the Earth and Sun[M]. Cambridge: Cambridge University Press. |
| [54] | Oncescu M C, Burlacu V, Anghel M, et al. 1984. Three-dimensional P-wave velocity image under the Carpathian Arc[J]. Tectonophysics, 106(3-4): 305-319. |
| [55] | Rawlinson N, Houseman G A. 1998. Inversion for interface structure using teleseismic traveltime residuals[J]. Geophys. J. Int., 133(3): 756-772. |
| [56] | Rawlinson N, Sambridge M. 2003. Seismic traveltime tomography of the crust and lithosphere[J]. Advances in Geophysics, 46: 81-198. |
| [57] | Rawlinson N, Sambridge M. 2005. The fast marching method: An effective tool for tomographic imaging and tracking multiple phases in complex layered media[J]. Exploration Geophysics, 36(4): 341-350. |
| [58] | Rawlinson N, Pozgay S, Fishwick S. 2010. Seismic tomography: A window into deep Earth[J]. Physics of the Earth and Planetary Interiors, 178(3-4): 101-135. |
| [59] | Reid F J L, Woodhouse J H, van Heijst H J. 2001. Upper mantle attenuation and velocity structure from measurements of differential S phases[J]. Geophys. J. Int., 145(3): 615-630. |
| [60] | Romanowicz B, Gung Y. 2002. Superplumes from the core-mantle boundary to the lithosphere: implications for heat flux[J]. Science, 296(5567): 513-516. |
| [61] | Ronchi C, Iacono R, Paolucci P S. 1996. The “Cubed Sphere”: A new method for the solution of partial differential equations in spherical geometry[J]. J. Comput. Phys., 124(1): 93-114, doi: 10.1006/jcph.1996.0047. |
| [62] | Saltzer R L, Humphreys E D. 1997. Upper mantle P wave velocity structure of the eastern Snake River Plain and its relationship to geodynamic models of the region[J]. Journal of Geophysical Research, 102(B6): 11829-11841. |
| [63] | Sambridge M, Braun J, McQueen H. 1995. Geophysical parametrization and interpolation of irregular data using natural neighbours[J]. Geophys. J. Int., 122(3): 837-857. |
| [64] | Sambridge M, Gudmundsson ó. 1998. Tomographic systems of equations with irregular cells[J]. Journal of Geophysical Research, 103(B1): 773-781. |
| [65] | Sambridge M, Faletič R. 2003. Adaptive whole Earth tomography[J]. Geochem. Geophys. Geosyst., 4(3), doi: 10.1029/2001GC000213. |
| [66] | Sambridge M S. 1990. Non-linear arrival time inversion: Constraining velocity anomalies by seeking smooth models in 3-D[J]. Geophys. J. Int., 102(3): 653-677. |
| [67] | Scott J S, Masters T G, Vernon F L. 1994. 3-D velocity structure of the San Jacinto fault zone near Anza, California-I. P waves[J]. Geophys. J. Int., 119(2): 611-626. |
| [68] | Shalev E. 1993. Cubic B-splines: Strategies of translating a simple structure to B-spline parameterization[J]. Bull. Seismol. Soc. Am., 83(5): 1617-1627. |
| [69] | Simons F J, Loris I, Nolet G, et al. 2011. Solving or resolving global tomographic models with spherical wavelets, and the scale and sparsity of seismic heterogeneity[J]. Geophys. J. Int., 187(2): 969-988. |
| [70] | Spakman W, Bijwaard H. 2001. Optimization of cell parameterizations for tomographic inverse problems[J]. Pure and Applied Geophysics, 158(8): 1401-1423. |
| [71] | Thomson C J, Gubbins D. 1982. Three-dimensional lithospheric modelling at NORSAR: linearity of the method and amplitude variations from the anomalies[J]. Geophys. J. Int., 71(1): 1-36. |
| [72] | Thurber C H. 1983. Earthquake locations and three-dimensional crystal structure in the Coyote lake area, central California[J]. Journal of Geophysical Research, 88(B10): 8226-8236. |
| [73] | Thurber C H, Aki K. 1987. Three-dimensional seismic imaging[J]. Annual Review of Earth and Planetary Sciences, 15(1): 115-139. |
| [74] | Tikhonov A N, Arsenin V Y. 1977. Solutions of ill-Posed Problems[M]. Washington D C: Winston and Sons. |
| [75] | Tikhotsky S, Achauer U. 2008. Inversion of controlled-source seismic tomography and gravity data with the self-adaptive wavelet parametrization of velocities and interfaces[J]. Geophys. J. Int., 172(2): 619-630, doi: 10.1111/j.1365-246X.2007.03648.x. |
| [76] | Trampert J, Woodhouse J H. 1995. Global phase velocity maps of Love and Rayleigh waves between 40 and 150 seconds[J]. Geophys. J. Int., 122(2): 675-690. |
| [77] | Trampert J, Snieder R. 1996. Model estimations biased by truncated expansions: possible artifacts in seismic tomography[J]. Science, 271(5253): 1257-1260. |
| [78] | Trinks I, Singh S C, Chapman C H, et al. 2005. Adaptive traveltime tomography of densely sampled seismic data[J]. Geophys. J. Int., 160(3): 925-938. |
| [79] | van der Hilst R D, Widiyantoro S, Engdahl E R. 1997. Evidence for deep mantle circulation from global tomography[J]. Nature, 386(6625): 578-584. |
| [80] | Vasco D W, Johnson L R. 1998. Whole earth structure estimated from seismic arrival times[J]. Journal of Geophysical Research, 103(B2): 2633-2671. |
| [81] | Vesnaver A, BÖhm G. 2000. Staggered or adapted grids for seismic tomography[J]. The Leading Edge, 19(9): 944-950. |
| [82] | Vesnaver A L. 1996. Irregular grids in seismic tomography and minimum-time ray tracing[J]. Geophysical Journal International, 126(1): 147-165. |
| [83] | Voronoi M. 1907. Nouvelles applications des paramètres continus à la théorie des formes quadratiques [J]. Journal für die Reine und Angewandte Mathematik, 133: 97-178. |
| [84] | Wang W H, Houseman G A. 1994. Inversion of reflection seismic amplitude data for interface geometry[J]. Geophys. J. Int., 117(1): 92-110. |
| [85] | Wang Z, Dahlen F A. 1995. Spherical-spline parameterization of three-dimensional Earth models[J]. Geophysical Research Letters, 22(22): 3099-3102. |
| [86] | Wang Z, Tromp J, Ekstr m G. 1998. Global and regional surface-wave inversions: A spherical-spline parameterization[J]. Geophys. Res. Lett., 25(2): 207-210. |
| [87] | White D J. 1989. Two-dimensional seismic refraction tomography[J]. Geophys. J. Int., 97(2): 223-245. |
| [88] | Wiggins S M, Dorman L M, Cornuelle B D, et al. 1996. Hess deep rift valley structure from seismic tomography[J]. J. Geophys. Res., 101(B10): 22335-22353. |
| [89] | Williamson P R. 1990. Tomographic inversion in reflection seismology[J]. Geophys. J. Int., 100(2): 255-274. |
| [90] | Wu J P, Yang T, Wang W L, et al. 2013. Three dimensional P-wave velocity structure around Xiaojiang fault system and its tectonic implications[J]. Chinese Journal of Geophysics (in Chinese), 56(7): 2257-2267, doi: 10.6038/cjg20130713. |
| [91] | Xu Y, Liu J H, Liu F T, et al. 2006. Crustal velocity structure and seismic activity in the Tianshan Pamir conjunctive zone[J]. Chinese Journal of Geophysics (in Chinese), 49(2): 469-476. |
| [92] | Xu Y, Yang X T, Liu J H. 2013. Tomographic study of crustal velocity structures in the Yunnan region southwest China[J]. Chinese Journal of Geophysics (in Chinese), 56(6): 1904-1914, doi: 10.6038/cjg20130613. |
| [93] | Yang X T, Xu Y, Liu J H, et al. 2011. Seismic tomography in the Tengchong volcanic area and its tectonic implication[J]. Chinese Journal of Geophysics (in Chinese), 54(8): 2050-2059, doi: 10.3969/j.issn.0001-5733.2011.08.012. |
| [94] | Zelt C A, Smith R B. 1992. Seismic traveltime inversion for 2-D crustal velocity structure[J]. Geophys. J. Int., 108(1): 16-34. |
| [95] | Zhang H J, Thurber C. 2005. Adaptive mesh seismic tomography based on tetrahedral and Voronoi diagrams: application to Parkfield, California [J]. Journal of Geophysical Research, Solid Earth (1978-2012), 110: B04303, doi: 10.1029/2004JB003186. |
| [96] | Zhao D P, Hasegawa A, Horiuchi S. 1992. Tomographic imaging of P and S wave velocity structure beneath Northeastern Japan[J]. Journal of Geophysical Research, Solid Earth (1978-2012), 97(B13): 19909-19928. |
| [97] | Zhao D P, Hasegawa A, Kanamori H. 1994. Deep structure of Japan subduction zone as derived from local, regional, and teleseismic events[J]. Journal of Geophysical Research, Solid Earth (1978-2012), 99(B11): 22313-22329. |
| [98] | Zhou H W. 1996. A high-resolution P wave model for the top 1200 km of the mantle[J]. Journal of Geophysical Research, 101(B12): 27791-27810. |
| [99] | Zhou H W. 2003. Multiscale traveltime tomography[J]. Geophysics, 68(5): 1639-1649. |
| [100] | Zhu L P, Zeng R S, Liu F T. 1990. A new model parameterization method for inversion of 3-Dimensional velocity structure[J]. Progress in Geophysics (in Chinese), 33(1): 34-43. |
| [101] | 曹令敏, 胥颐, 吴时国. 2013. 腾冲地区地壳速度结构的有限差分成像[J]. 地球物理学报, 56(4): 1159-1167, doi: 10.6038/cjg20130411. |
| [102] | 范建柯, 吴时国. 2014. 马尼拉俯冲带的地震层析成像研究[J]. 地球物理学报, 57(7): 2127-2137, doi: 10.6038/cjg20140709. |
| [103] | 郭飚. 2003. 流动宽频带地震台阵: 地震定位与地震层析成像[D]. 北京: 中国地震局地质研究所. |
| [104] | 郭飚, 刘启元, 陈九辉,等. 2009. 川西龙门山及邻区地壳上地幔远震P波层析成像[J]. 地球物理学报, 52(2): 346-355. |
| [105] | 刘福田, 李强, 吴华,等. 1989. 用于速度图象重建的层析成象法[J]. 地球物理学报, 32(1): 46-61. |
| [106] | 刘建华, 吴华, 刘福田. 1996. 华南及其海域三维速度分布特征与岩石层结构[J]. 地球物理学报, 39(4): 483-492. |
| [107] | 吴建平, 杨婷, 王未来,等. 2013. 小江断裂带周边地区三维P波速度结构及其构造意义[J]. 地球物理学报, 56(7): 2257-2267, doi: 10.6038/cjg20130713. |
| [108] | 胥颐, 刘建华, 刘福田,等. 2006. 天山-帕米尔结合带的地壳速度结构及地震活动研究[J]. 地球物理学报, 49(2): 469-476. |
| [109] | 胥颐, 杨晓涛, 刘建华. 2013. 云南地区地壳速度结构的层析成像研究[J]. 地球物理学报, 56(6): 1904-1914, doi: 10.6038/cjg20130613. |
| [110] | 杨晓涛, 胥颐, 刘建华,等. 2011. 腾冲火山区的地震层析成像及其构造意义[J]. 地球物理学, 54(8): 2050-2059, doi: 10.3969/j.issn.0001-5733.2011.08.012. |
| [111] | 朱露培, 曾融生, 刘福田. 1990. 一种新的三维速度结构反演模型参数化方法[J]. 地球物理学进展, 33(1): 34-43. |
 2015, Vol. 30
2015, Vol. 30

