2. 犹他大学矿产和地球科学学院, 盐湖城 84112, 美国
2. College of Mines & Earth Sciences the University of Utah, Salt Lake City 84112, USA
复电阻率(complex resistivity CR)法是通过测量一系列频点上大地复电阻率的虚、实分量(或振幅、相位)寻找电性异常体的一种电法勘探方法.如何对获取的实际激电数据进行精确的解释已经成为当今电磁法研究领域的一个热点问题(Yoshioka and Zhdanov,2005;岳安平等,2009;程辉等,2010;Tarasov and Titov,2013;Tang et al.,2014).Pelton于1978首次提出采用多频率测量消除电磁耦合,并且对含矿及非矿岩石进行区分的一种研究方法,初步奠定了频谱激电的理论研究基础.国内著名电法学者罗延钟从岩、矿石中导电离子的电化学机理出发,采用Cole-Cole模型提出了利用时间常数及频谱相关系数对极化异常体进行结构区分的基本思想(罗延钟和吴之训,1992),并且对非各向同性二层大地中的三维极化体进行正演计算,导出了面极化和体极化频谱激电的模拟相似准则(罗延钟和张桂青,1988).现阶段,对复电阻率的数值模拟研究思路可以大致分为两种:其一是在忽略电磁感应条件下,求解瞬态直流电场满足的泊松方程进行正演计算(阮百尧和罗润林,2003;蔡军涛等,2007;李勇等,2011b);其二是同时考虑激电效应和电磁感应,在频率域中求解满足亥姆霍兹方程(Helmholtz Equation)及大地边值问题的数值解(罗延钟等,2003;杨晓弘等,2008;李建平,2008;李勇等,2011a;范翠松等,2012;Xu,2013).
从现今已有的研究成果分析,相关算法的提出都是基于假设地下介质电导率用一个随频率变化的松弛模型而建立的,并且绝大多数是利用岩、矿石离子的电化学性质通过物理等效而来,这些模型诸如Cole-Cole(Yuval and Oldenburg,1997)、复Cole-Cole(徐汶东等,2013)、Dias(丁柱等,2005)、Fractal模型(Farias et al.,2005,2013)都是在微粒或者显微尺度下对激发极化效应进行近似研究,得出的若干个参数所表示的意义多为定性描述,而缺乏与之对应的相关实际岩石学参数.基于此,美国犹他大学Zhdanov教授及其所在的CEMI(The Center for Electromagnetic Modeling and Inversion)课题组通过对大量的不同种类的岩、矿石进行测量(Emond et al.,2006;Zhdanov et al.,2008),结合广义等效介质理论推导出了一种用以描述岩、矿石激发极化效应的统一的严格物理数学模型即GEMTIP模型(Zhdanov,2008,2009).它是常规Cole-Cole模型的广义表述,并且将岩、矿石的一些基本结构及岩石学特征在宏观尺度进行表示,其参数与岩、矿石的物理属性相关联,为区分多相复合岩、矿石提供了一种定量的分析方法.近些年来,GEMTIP模型的理论研究受到普遍的关注,也取得了较为丰硕的研究成果,而研究的主要内容还主要集中在对具有激电效应岩、矿石样品的参数反演验证及低维度的数值模拟方面,就研究方法而言也仅局限于单一的积分方程法(Phillips,2010,Fu,2013).本文在吸收前人工作的基础上,将这种GEMTIP模型引入到2.5维复电阻率数值模拟中,正演计算方法采用已在流体力学及热扩散领域广泛应用的有限体积法(李人宪,2005),其具有离散形式简单,计算精度较高,各项具有明确的物理意义等优点,构建若干典型的复电阻率地电模型及相关的实例模型,通过分析响应的异常特征,以期为解释分析激发极化效应提供一种新的研究思路.
1 GEMTIP模型图 1给出了典型的石英二长斑岩在等效介质理论下复电阻率的等效原理图.当岩石基质中矿物可以视作不同半径的球形颗粒时,给定相关的岩石学及流变特征参数,在岩石宏观尺度上其复电阻率可以用一个统一的数学解析表达式进行表述(Zhdanov et al.,2012),公式为.
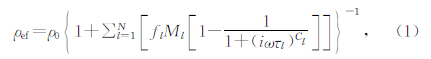


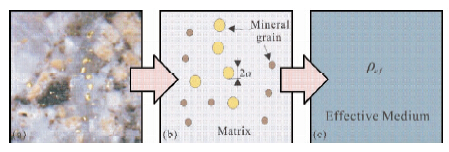 |
图 1 岩矿石复电阻率等效原理[据(Zhdanov,2008)修编] (a)石英二长斑岩切片;(b)多相态矿物颗粒球形近似; (c)等效复电阻率. Fig. 1 The schematic of effective of rock and ore complex resistivity that editing and revision based on(Zhdanov,2008) (a)The slice of a quartz monzonite porphyry rock; (b)Multiphase mineral grains spherical approximation; (c)The effective complex resistivity. |
图 2中表示为给定岩、矿石相关参数,研究面极化系数α及体积百分数f对视复电阻率频谱曲线的影响.Model1参数设置为:ρ0=100 Ω·m、C1=0.8、ρ1=0.4 Ω·m、a1=3 mm、α1分别为0.04、0.2、1、2、4,单位为(Ω·m2)/sec2;Model2参数设置为:α1=0.8(Ω·m2)/sec2、f1分别为0.1、0.2、0.3、0.4、0.5,其余的参数与Model1相同.就视复电阻率的实部分量而言,随着频率的逐渐增加其幅值均由零频电阻率ρ0单调递减至某一值后趋于稳定;面极化系数α越大,曲线开始下降时所对应的频率值越大;体积百分数f逐渐增加曲线最终趋于的稳定电阻率的值逐渐变小.分析视复电阻率的虚部分量曲线可知,所有的曲线均在某一频率达到极小值,将该频率定义为fMax;当面极化系数α增大时,fMax亦随之增大;当体积百分数f依次增大,其对应的fMax变化较小,但其极小值逐渐减小.
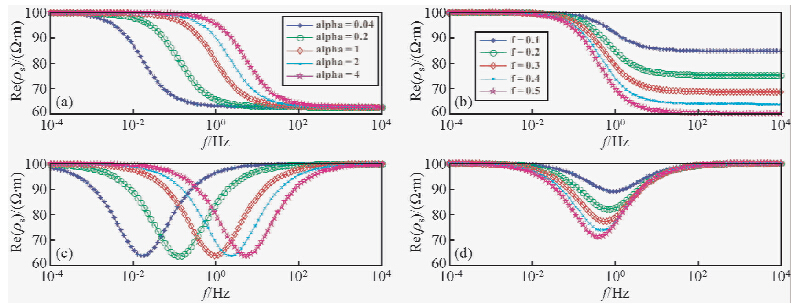 |
图 2 模型计算频谱变化曲线 (a)与(c)为Model1计算结果;(b)与(d)为Model2计算结果. Fig. 2 Spectrum curves through calculating the models (a) and (c)The result of Model1,(b) and (d)The result of Model2. |
由此可以看出,不同的岩、矿石可以用不同的GEMTIP模型参数近似的等效,通过数值计算,进而可以对其差异作定量的区分.
2 有限体积法
2.1 基本控制方程
地下介质的复电阻率可以采用常规的电法装置,通过向地下供给一定频率的交流电,在地表进行测量得到,忽略电磁感应,其复电位满足的基本控制方程为
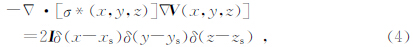
假设地下导电性构造沿走向方向无变化(y方向),这样,σ*(x,y,z)就可以写成σ*(x,z),对公式(4)两边进行傅里叶变换即可得到波数域中复电位满足的控制方程为
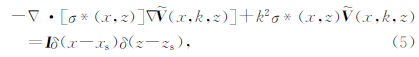
 为波数域中复电位,k为波数.
为波数域中复电位,k为波数.
可以通过离散的傅里叶反变换将 转换到空间域中,公式为
转换到空间域中,公式为

|
|
表 1 傅里叶反变换的k和g Table 1 k and g parameters of Fourier inverse transform |
图 3为二维问题网格系统的一部分,图中阴影区域为节点P的控制容积.控制容积的形成采用节点中心方式,节点P到节点W、E、N、S的距离分别用δxWP、δxPE、δzPN、δzSP表示,w、e、n、s分别取在点W-P、P-E、P-N、S-P的中间即控制容积的边界处.
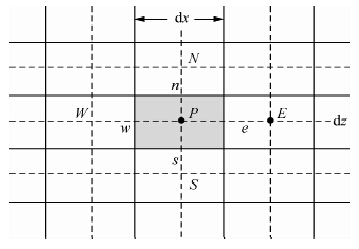 | 图 3 有限体积二维网格系统 Fig. 3 Two-dimensional grid system of finite volume |
根据有限体积法基本思想,在控制容积中对方程式(5)进行体积分,得到
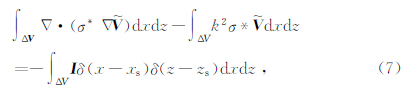
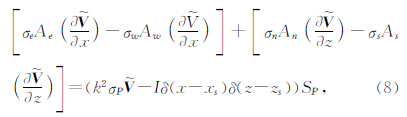
对于公式(8)中的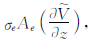 有
有
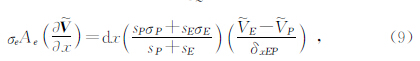
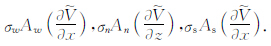
对二维网格内部节点满足的控制方程进行上述离散即可得到相应的线性方程组为
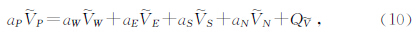

在地表单元采用Neumann边界条件,无穷远边界采用混合边界条件为

将边界条件(12)和(13)代入到公式(10)中得到总体有限体积线性方程组.采用不完全的LU分解及预处理的广义极小残差算法(GMRES)对大型稀疏非对称线性方程组进行求解,进而得到各节点上波数域复电位,再利用公式(6)对其进行离散傅里叶反变换即可得到空间域中所有节点上的复电位.
2.3 计算视复电阻率
在频率、供电及测量点位已知的情况下,利用上述数值求解得到的各节点上复电位的值,采用公式(14)即可计算相应的视复电阻率为
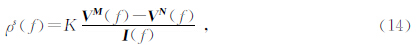
3 若干算例
这里采用上述有限体积算法进行正演计算,使用GEMTIP模型对复电阻率的频率响应进行定量描述.本文的算例中选用的四个频率按2n系列伪随机原理(何继善,2010)选取,其值分别为:f1=2k、f2=2k+1、f3=2k+2、f4=2k+3,其中k=-3,频率的单位为Hz.依照已知测试的岩、矿物GEMTIP模型各参数,首先构建两相的水平层状模型对数值计算程序的有效性进行验证,其次构建均匀大地赋存三相低阻极化块模型、三相地堑模型及简化斑岩型矿床模型,采用电磁耦合较小的偶极-偶极装置进行测量,通过计算不同频率下的视复电阻率响应,绘制其实部分量、虚部分量(或振幅,相位)的拟断面图,并对相应的异常特征进行对比分析.
3.1 两相水平层状模型
表 2中列出了水平层状大地的GEMTIP模型相关参数,这里等效的复电阻率是两相态的基岩与矿物的综合反映,当频率f=1 Hz时,采用快速Hankel积分算法计算在对称四极装置下的两层大地视复电阻率测深曲线(席振铢等,2003).将其与利用本文所述数值算法计算得到的视复电阻率曲线进行比较.从图 4a与4b可以看出,由于采用增强波数及加权系数的原因,无论是近源处还是在近边界处,数值计算得到的视复电阻率实部分量及虚部分量与解析解均拟合较好,因此可以证明本文所编制有限体积程序的有效性及正确性.
|
|
表 2 水平层状模型参数 Table 2 Basicparameters |
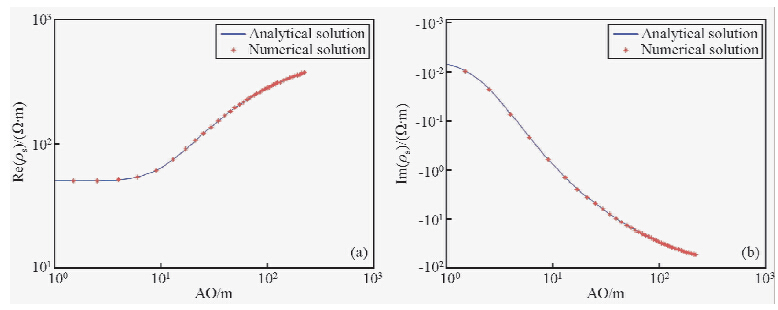 |
图 4 有限体积数值解与解析解对比 (a)视复电阻率实部;(b)视复电阻率虚部. Fig. 4 Comparison of FVM-numerical solution withanalyticalsolution (a)Real component of apparent complex resistivity;(b)Imaginary component of apparent complex resistivity. |
图 5表示为均匀大地中赋存三相低阻极化块模型的空间展布情况.与之相对应的GEMTIP模型参数如表 3所示.实际测量偶极距AB=MN=2 m,电极距倍数n=1~10.在伪随机产生的四个频点上,正演计算得到的视复电阻率实部分量、视复电阻率虚部分量拟断面如图 6所示.
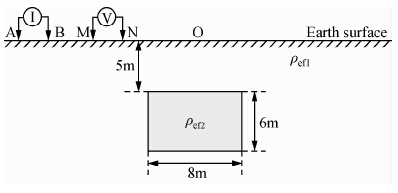 | 图 5 低阻极化块模型 Fig. 5 Low resistance and polarization block model |
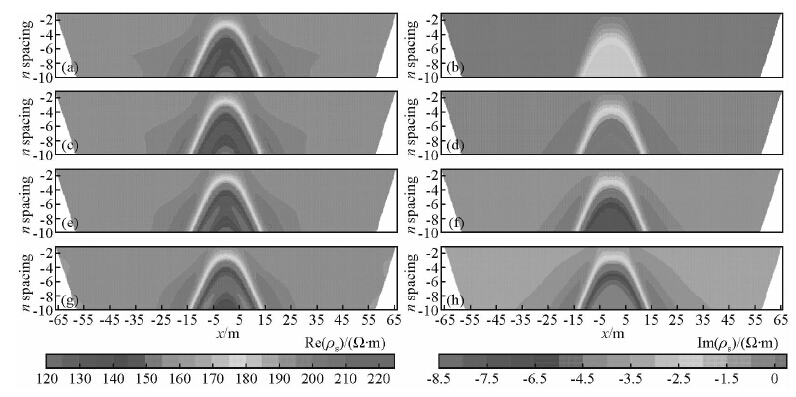 |
图 6 给定频率的视复电阻率实部(左列)和虚部(右列)拟断面图 (a)与(b)0.125 Hz;(c)与(d)0.25 Hz;(e)与(f)0.5 Hz;(g)与(h)1 Hz. Fig. 6 The pseudosection of real component of apparent complex resistivity(left column) and imaginary component of apparent complex resistivity(right column)for giving the frequencies (a) and (b)0.125 Hz;(c) and (d)0.25 Hz;(e) and (f)0.5 Hz;(g) and (h)1 Hz. |
|
|
表 3 低阻极化块模型参数 Table 3 The parameters of low resistance and polarization block model |
从图 6中可以明显的看出,无论是视复电阻率的实部分量还是虚部分量,低阻高极化块在偶极-偶极测量装置下的视电阻率异常响应均呈现典型的“八”字形特征.视复电阻率虚部分量为负值,并且随着频率的逐渐增大,其视复电阻率实部分量及虚部分量幅值均逐渐增加,相较而言,视复电阻率虚部分量增加幅度较大.
3.3 三相地堑模型这里构建三相的地堑模型,其空间几何参数如图 7所示,GEMTIP模型参数见表 4,实际测量偶极距AB=MN=2 m,电极距倍数n=1~10.数值模拟得到的视复电阻率的实部分量及虚部分量拟断面如图 8所示.从图 8中可以看出,在不同频率情况下,其视复电阻率的实部分量及虚部分量的响应特征均呈现“凹陷”状.通过与实际的模型进行比较,数值计算所得场值分布情况可以大致推断相应的异常体的位置及几何形态.
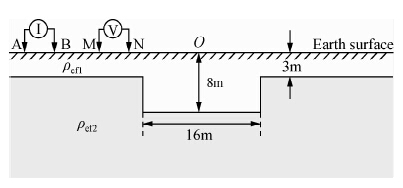 | 图 7 地堑模型 Fig. 7 Graben model |
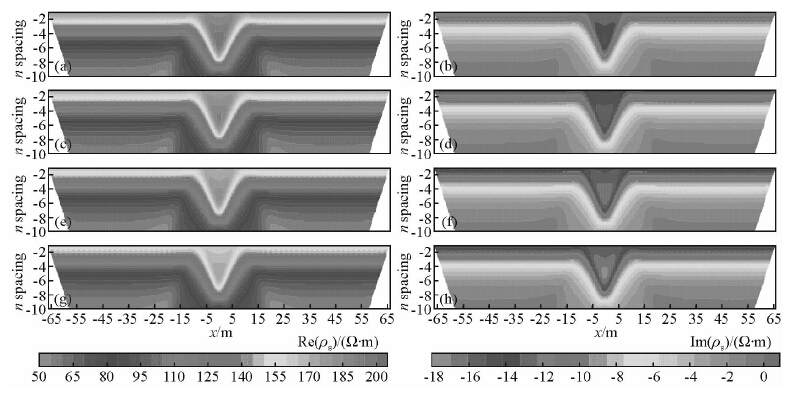 |
图 8 给定频率的视复电阻率实部(左列)和虚部(右列)拟断面图 (a)与(b)0.125 Hz;(c)与(d)0.25 Hz;(e)与(f)0.5 Hz;(g)与(h)1 Hz. Fig. 8 The pseudosection of real component of apparent complex resistivity(left column) and imaginary component of apparent complex resistivity(right column)for giving the frequencies (a) and (b)0.125 Hz;(c) and (d)0.25 Hz;(e) and (f)0.5 Hz;(g) and (h)1Hz. |
|
|
表 4 地堑模型参数 Table 4 The parameters of trough model |
图 9表示为简化的斑岩型矿床的模型示意,此模型是层状地质背景下典型的斑岩热液型成矿模式的简要描述,Emond(2007)在总结前人研究成果基础上进行了地球物理模型的近似,同时采用X射线层析扫描成像技术测定了相关GEMTIP各参数,本例即选用此模型,与模型对应的地质单元设置及物性参数见表 5.其中矿富集区和黄铜矿化带中所含矿物为黄铜矿,黄铁矿壳内的主要矿物为黄铁矿.实际 测量参数为:偶极距AB=MN=200 m、 测线总长度为5400 m,其余参数如前例相同.正演计算得到的不同频点下的视复电阻率的振幅及相位拟断面如图 10所示.
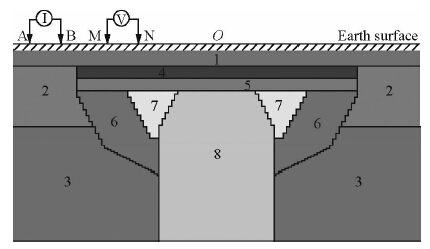 | 图 9 简化斑岩型矿床模型 Fig. 9 Simplified porphyry deposit model |
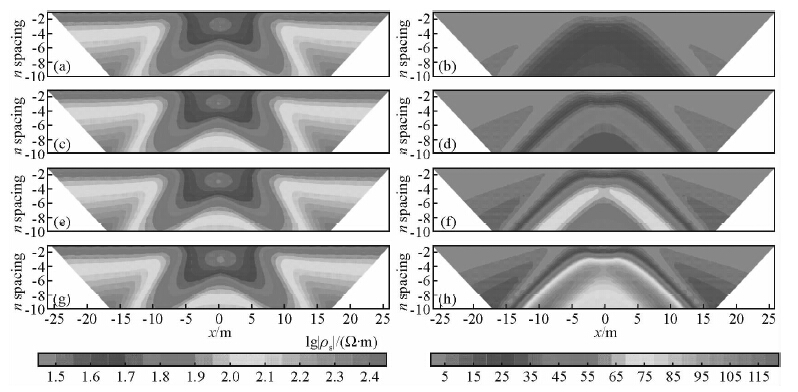 |
图 10 给定频率的视复电阻率振幅(左列)和相位(右列)拟断面图 (a)与(b)0.125 Hz;(c)与(d)0.25 Hz;(e)与(f)0.5 Hz;(g)与(h)1 Hz. Fig. 10 The pseudosection of amplitude of apparent complex resistivity(left column) and phase of apparent complex resistivity(right column)for giving the frequencies (a) and (b)0.125 Hz;(c) and (d)0.25 Hz;(e) and (f)0.5 Hz;(g) and (h)1 Hz. |
|
|
表 5 简化斑岩型矿床模型参数 Table 5 The parameters of simplified porphyry deposit model |
从图 10中可以明显的看出,不同频率下的视复电阻率振幅拟断面形态基本一致,均在中间呈现块状低阻区域,并且随着电极距倍数的增加向两侧逐渐延伸,就水平方向分析其异常边界与矿富集区边界有很好的对应关系,较好的提供了含矿地质体的水平扩展信息,但垂向深度上则与实际相差较大,可见其水平分辨率要大于垂向分辨率.而相位拟断面则随着测量频率的逐渐增加其异常形态变得较为复杂,与此同时相位值亦相应增大,两侧高相位异常带关于中心线对称,呈“马鞍”形,这主要是由于在矿富集区、黄铁矿壳及黄铜矿化带中具有激发极化效应的金属硫化岩体共同作用的结果.这与Emond(2007)采用基于积分方程法的IBCEM3DIP程序计算结果进行比较分析可知,忽略网格剖分及倾斜岩(矿)层实际厚度或宽度设置的微小差别,两种算法数值模拟得到的复视电阻率的振幅及相位拟断面异常特征基本吻合.
4 结 论将地下岩、矿体的复电阻率用GEMTIP模型进行等效,本文实现了基于有限体积法的CR数值模拟,通过与相应解析解对比,验证了算法的正确性,分析多频点不同参数对视复电阻率的测深曲线及拟断面的异常响应影响,得出以下几点结论:
(1)GEMTIP模型将岩、矿体固有的一些岩石学特征纳入到岩、矿体激发极化效应研究中是可行的,这为在宏观尺度上进一步阐释激发极化效应方面具有很好的前景.
(2)对构建的多相态复合模型及实际的简化斑岩型矿床模型进行数值模拟,结果显示,在一定的频率范围内视复电阻率虚部为负值,并且随着频率的逐渐增大其幅值亦相应增加,综合视复电阻率振幅及相位反映的信息可知,其对激电异常体的探测水平分辨率明显优于垂向分辨率.
(3)有限体积法为频率域2.5维激电法数值模拟提供了高效精确的算法,在不同频率条件下,GEMTIP模型反映的岩石学特征较为明显,根据计算场值的分布情况可以对实际野外获取的激发激化数据进行初步的地质解释.
(4)本文是在忽略电磁耦合的理想情况下进行的相关研究,诚然,在实际的频谱激电测量中这一部分是不能够被忽略的,因此考虑电磁耦合效应的基于GEMTIP模型的2.5维多参数联合反演将是后续研究的重要方向.
致 谢 感谢国家自然科学基金委、桂林市“漓江学者”对本项研究课题提供的经费资助;两位匿名审稿人为文章的修改提供了一些宝贵建议,特此感谢.| [1] | Cai J T, Ruan B Y, Zhao G Z, et al. 2007. Two-dimensional modeling of complex resistivity using finite element method[J]. Chinese Journal of Geophysics (in Chinese), 50(6): 1869-1876, doi:10.3321/j.issn:0001-5733.2007.06.030. |
| [2] | Cheng H, Di Q Y, Li D Q. 2010. The discussion electrical properties of rocks base on frequency response characteristics[J]. Progress in Geophysics (in Chinese), 25(3): 918-925, doi:10.3969/j.issn.1004-2903.2010.03.027. |
| [3] | Ding Z, Tong M S, Pan S. 2005. The Dias model of rock complex resistivity and its parameter inversionmethod[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 27(2): 135-137. |
| [4] | Emond A M, Zhdanov M S, Petersen E U. 2006.Electromagnetic modeling based on the rock physics description of the true complexity of rocks: applications to study of the IP effect in porphyry copper deposits[C].SEGExpanded Abstracts,1313-1317. |
| [5] | Emond A M. 2007. Electromagnetic modeling of porphyry systems form the grain-scale to the deposit-scale using the generalized effective medium theory of induced polarization[D]. Salt Lake City: The University of Utah. |
| [6] | Fan C S, Li T L, Yan J Y. 2012. Research and application experiment on 2. 5D SIP inversion[J]. Chinese Journal of Geophysics (in Chinese), 55(12): 4044-4050, doi:10.6038/j.issn.0001-5733.2012.12.016. |
| [7] | Farias V J C, da Rocha B R P. 2005. Induced polarization modelling using the fractal model to complex resistivity for environmental application[J]. Journal of Environmental Informatics, 6(1): 25-32. |
| [8] | Farias V J C, da Rocha B R P, da Rocha M P C, et al. 2013. The use of the fractal model to complex resistivity in the interpretation of induced polarization data[J]. Applied Mathematical Modelling, 37(3): 1347-1361. |
| [9] | Fu H Y. 2013. Interpretation of complex resistivity of rocks using GEMTIP analysis[D]. Salt Lake City:The University of Utah. |
| [10] | He J S. Closed addition in a three-element set and 2n sequence pseudo-random signal coding[J]. Journal of Central South University (Science and Technology) (in Chinese), 2010, 41(2): 632-637. |
| [11] | Li J P. 2008. Research on electromagnetic modeling of 3D complex resistivity with topography (in Chinese) [D].Changchun: Jilin University. |
| [12] | Li R X. 2005. The Foundation of Finite Volume Method (in Chinese) [M].Beijing: National Defense Industry Press. |
| [13] | Li Y, Lin P R, Xiao Y, et al. 2011a. Induced polarization effect on frequency-domain electromagnetic sounding with electric dipole source[J]. Chinese Journal of Geophysics (in Chinese), 54(7): 1935-1944, doi:10.3969/j.issn.0001-5733.2011.07.028. |
| [14] | Li Y, Lin P R, Li T L, et al. 2011b. Finite element method for solving anomalous complex potential of 2.5-D complex resistivity[J]. Journal of Jilin University(Earth Science Edition) (in Chinese), 41(1): 1596-1604. |
| [15] | Luo Y Z, Zhang G Q. 1988. The Principle of Frequency Domain IP Method (in Chinese) [M].Beijing: Geological Publishing House. |
| [16] | Luo Y Z, Wu Z X. 1992. The application of frequency dependent factor in spectral induced polarization method[J]. Acta Geophysica Sinica(in Chinese), 35(4): 490-500. |
| [17] | Luo Y Z, Zhang S Y, Xiong B. 2003. Feasibility of natural source induced polarization[J]. Chinese Journal of Geophysics (in Chinese), 46(1): 125-130, doi:10.3321/j.issn:0001-5733.2003.01.020. |
| [18] | Pelton W H, Ward S H, Hallof P G, et al. 1978. Mineral discrimination and removal of inductive coupling with multifrequency IP [J].Geophysics, 43(3): 588-609. |
| [19] | Phillips C R. 2010.Experimental study of the induced polarization effect using Cole- Cole and GEMTIP models [D]. Salt Lake City: The University of Utah. |
| [20] | Ruan B Y, Luo R L. 2003. A new recursive invresion method of the complex-resistivity spectrum[J]. Computing Techniques for Geophysical and Geochemical Exploration(in Chinese), 25(4): 298-301. |
| [21] | Tang J T, Wang F Y, Xiao X, et al. 2011. 2. 5-D DC resistivity modeling considering flexibility and accuracy[J]. Journal of Earth Science, 22(1): 124-130. |
| [22] | Tang R. Yu P, Xiang Y, et al. 2014. The sensitivity analysis of different induced polarization models used in magnetotelluricmethod[J]. Acta GeodaeticaetGeophysica, 49(2): 225-233. |
| [23] | Tarasov A, Titov K. 2013. On the use of the Cole-Cole equations in spectral induced polarization[J]. Geophysical Journal International, 195(1): 352-356. |
| [24] | Xi Z Z, Zhang Y S, Zhang X R. 2003. Spectral characteristics of multifrequency IP sounding with schlumberger array over a multi-layered polarization earth[J]. Journal of Central South University Technology (Nature Science) (in Chinese), 34(1): 8-10. |
| [25] | Xu P D, Li J Z, Yu L. 2013. Spectrum difference research and analysis of two kinds of compound Cole-Cole models[J]. Journal of Shandong University of Technology (Natural Science Edition) (in Chinese), 27(5): 5-9. |
| [26] | Xu Z W. 2013.Three-dimension Cole-Cole model inversion of induced polarization data based on regularized conjugate gradient method [D]. Salt Lake City: The University of Utah. |
| [27] | Yang B, Xu Y X, He Z X, et al. 2012.3D frequency-domain modeling of marine controlled source electromagnetic responses with topography using finite volume method[J]. Chinese Journal of Geophysics (in Chinese), 55(4): 1390-1399, doi: 10.6038/j. issn.0001-5733.2012.04.035. |
| [28] | Yang X H, He J S, Tong X Z. 2008.Numerical simulation of frequency-domain IP with FEM[J]. Progress in Geophysics (in Chinese), 23(4): 1186-1189. |
| [29] | YoshiokaK, Zhdanov M S.2005. Three-dimensional nonlinear regularized inversion of the induced polarization data based on the Cole-Cole model[J]. Physics of the Earth and Planetary Interiors, 150(1-3): 29-43. |
| [30] | Yue A P, Di Q Y, Wang M Y,et al. 2009. 1-D forward modeling of the CSAMT signal incorporating IP effect[J]. Chinese Journal of Geophysics (in Chinese), 52(7): 1937-1946, doi:10.3969/j.issn.0001-5733.2009.07.030. |
| [31] | Yuval, Oldenburg D W. 1997. Computation of Cole-Cole parameters from IP data[J]. Geophysics, 62(2): 436-448. |
| [32] | Zhdanov M.2008. Generalized effective-medium theory of induced polarization[J]. Geophysics, 73(5): F197-F211. |
| [33] | Zhdanov M S, Gribenko A, BurtmanV.2008. Anisotropy of induced polarization in the context of the generalized effective-medium theory[C]// SEG Las Vegas 2008 Annual Meeting. Society of Exploration Geophysicists, 677-681. |
| [34] | Zhdanov M S. 2009.Geophysical Electromagnetic Theory and Methods[M]. Amsterdam Boston: Elsevier. |
| [35] | Zhdanov M S, Burtman V, Endo M, et al. 2012.Laboratory-based GEMTIP analysis of spectral IP data for mineral discrimination[C]SEG Technical Program Expanded Abstracts,1-5. |
| [36] | 蔡军涛, 阮百尧, 赵国泽,等. 2007. 复电阻率法二维有限元数值模拟[J]. 地球物理学报, 50(6): 1869-1876, doi:10.3321/j.issn:0001-5733.2007.06.030. |
| [37] | 程辉, 底青云, 李帝铨. 2010. 频率信号激励下岩石电性参数研究[J]. 地球物理学进展, 25(3): 918-925, doi:10.3969/j. issn.1004-2903.2010.03.027. |
| [38] | 丁柱, 童茂松, 潘涛. 2005. 岩石复电阻率Dias模型及其参数求取方法[J]. 物探与化探计算技术, 27(2): 135-137. |
| [39] | 范翠松, 李桐林, 严加永. 2012. 2.5维复电阻率反演及其应用试验[J]. 地球物理学报, 55(12): 4044-4050, doi: 10.6038/j.issn.0001-5733.2012.12.016. |
| [40] | 何继善. 2010. 三元素集合中的自封闭加法与2n系列伪随机信号编码[J]. 中南大学学报(自然科学版), 41(2): 632-637. |
| [41] | 李建平. 2008. 带地形的三维复电阻率电磁场正反演研究[D]. 长春: 吉林大学. |
| [42] | 李人宪. 2005. 有限体积法基础[M]. 北京: 国防工业出版社. |
| [43] | 李勇, 林品荣, 肖原,等. 2011a. 电偶源频率电磁测深激发极化效应研究[J]. 地球物理学报, 54(7): 1935-1944, doi:10. 3969/j.issn.0001-5733.2011.07.028. |
| [44] | 李勇, 林品荣, 李桐林,等. 2011b. 基于异常复电位2.5维CR有限元数值模拟[J]. 吉林大学学报(地球科学版), 41(5): 1596-1604. |
| [45] | 罗延钟,张桂青. 1988. 频率域激电法原理[M]. 北京:地质出版社. |
| [46] | 罗延钟, 吴之训. 1992. 谱激电法中频率相关系数的应用[J]. 地球物理学报, 35(4): 490-500. |
| [47] | 罗延钟, 张胜业, 熊彬. 2003. 天然场源激电法的可行性[J]. 地球物理学报, 46(1): 125-130, doi:10.3321/j.issn:0001-5733.2003.01.020. |
| [48] | 阮百尧, 罗润林. 2003. 一种新的复电阻率频谱参数的递推反演方法[J]. 物探与化探计算技术, 25(4): 298-301. |
| [49] | 席振铢, 张有山, 张宪润. 2003. 运用对称四极测深研究层状极化介质频谱特征[J]. 中南工业大学学报(自然科学版), 34(1): 8-10. |
| [50] | 徐汶东, 李敬兆, 于瓅. 2013. 两种复合Cole-Cole模型的频谱差异研究与分析[J]. 山东理工大学学报(自然科学版), 27(5): 5-9. |
| [51] | 杨波, 徐义贤, 何展翔,等. 2012. 考虑海底地形的三维频率域可控源电磁响应有限体积法模拟[J]. 地球物理学报, 55(4): 1390-1399, doi:10.6038/j.issn.0001-5733.2012.04.035. |
| [52] | 杨晓弘, 何继善, 童孝忠. 2008. 频率域激电有限元数值模拟[J]. 地球物理学进展, 23(4): 1186-1189. |
| [53] | 岳安平, 底青云, 王妙月,等. 2009. 含激电效应的CSAMT一维正演研究[J]. 地球物理学报, 52(7): 1937-1946, doi:10.3969/j.issn.0001-5733.2009.07.030. |
 2015, Vol. 30
2015, Vol. 30


