2. 北京印刷学院信息工程学院, 北京 102600
2. Beijing Institute of Graphic Communication, Beijing 102600, China
在石油工业中,需要比较准确地评价油气藏,需要了解油气藏的埋藏深度、分布状况以及地层孔隙度、渗透率和含水(油)饱和度等参数(Hungerford and Fay,1957; Kunz and Moran,1958;党瑞荣等,2006; 王昌学等,2013),感应测井在这方面起了重要作用,为油气藏评价提供了主要依据.传统的测井仪只测量地层的一个方向的特性,展示一个方向的电导率.自上世纪发现沉积地层的电性各向异性现象后的半个多世纪中,人们一直致力于利用不同仪器在各向异性地层中响应的差异性进行各向异性地层的识别(Kunz and Moran,1958;Moran and Kunz,1962; Moran and Gianzero,1979),但进展缓慢.直到1994年,Amoco公司Nekut(1994)设计了直接测量各向异性地层的感应测井仪,其线圈结构即是现在的多分量感应测井仪线圈结构雏形(Klein et al.,1997;Zhdanov et al.,2001).Atlas与Shell 公司在2001年联合推出多分量感应测井仪3DEX,3DEX,可测量五个磁场分量(Wang and Fang,2001;Gao et al.,2002; Wang et al.,2003).在国内,对各向异性地层的识别和评价包括仪器的制造正处于起步阶段(汪宏年等,2008,2012;肖加奇等,2013;张烨等,2012),中国石油长城钻探工程有限公司测井技术研究院已开展了三维阵列感应测井仪器的研发工作(俞燕明等,2013; 洪德成等,2013; 张国艳等,2012).三维感应测井仪器是由3个彼此垂直的发射线圈和与之平行的3个接收线圈组成,可以从三维角度识别地层特性,对薄储层、复杂储层的探测具有先天优势.目前国外已有大量文献阐述了三维感应测井的基础理论及数值计算(Davydycheva et al.,2003; Gao et al.,2002;Nam et al.,2010; Wang and Fang,2001;Wang et al.,2003,2006),但是国内这方面研究的文章则相对滞后.确定TI地层的各向异性指数因子对测井资料解释是极为重要的,例如含泥浆井眼的泥浆影响、井经影响等的校正,图版的选择,包括地层参数的反演等,都需要进行地层各向异性指数因子的预测与计算,但目前地层各向异性指数因子的预测与计算方法研究的很少,本文试图尽量利用少的三维感应测井视电导率资料实现地层各向异性指数因子的预测与计算,分别给出了图版法和牛顿迭代法实现地层各向异性指数因子的确定与计算,数值算例表明,计算结果与地层模型取得了很好的一致性,验证了方法的可行性与有效性.
1 三分量感应测井地层视电导率计算方法三分量维感应测井仪是由三个中心共点、彼此垂直的三个发射线圈和与其平行的三个接收线圈组成.当发射线圈系有交流信号流过时,在空间介质中产生交变电磁场,在该磁场中的接收线圈将产生感应电动势.可同时测量接收线圈系的感应电动势 V,并由此计算地层的视电导率

当三分量维感应测井仪的z-方向发射线圈发射,在z-方向线圈接收时,则接收线圈的电动势可写为(Moran and Kunz,1962; Moran and Gianzero,1979; Wang et al.,2006)
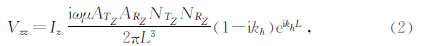
 为水平电导率,
为水平电导率,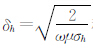 称为趋肤深度,L为电极距(发射、接收线圈间的距离).
称为趋肤深度,L为电极距(发射、接收线圈间的距离).
当三分量维感应测井仪的x-方向发射线圈发射,在x-方向线圈接收时,则x-方向接收线圈的电动势可写为(Moran and Kunz,1962; Moran and Gianzero,1979; Wang et al.,2006)
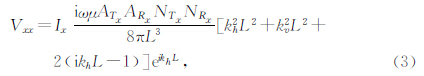
其中Ix 为 x-方向发射线圈中的电流,ATx、ARx为发射线圈、接收线圈的面积,NTx、NRx为发射线圈、接收线圈的匝数,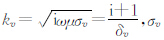 为垂直电导率,
为垂直电导率,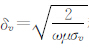 称为趋肤深度.
称为趋肤深度.
对三分量维感应测井仪的仪器系数可写为(Moran and Kunz,1962; Moran and Gianzero,1979; Wang et al.,2006)
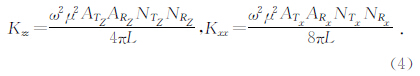
地层的视电导率为
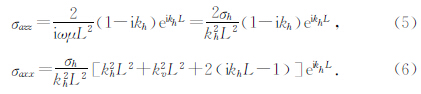
2.1 地层各向异性指数因子图版的制作
设x-方向发射线圈发射,x-方向线圈接收,则地层视电导率为

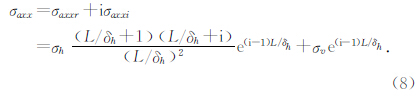
利用该式可制作各向异性地层指数因子图版.下面取两组参数分别介绍图版的制作方法及分析图版的特点.设电极电流为I0=6 A,电源频率f=2.5×104 Hz,电极距 L=0.55 m,真空中磁导率μ0=4π×10-7 N·A-2(或H·m-1),第一组地层参数: σh=0.1,0.2,0.4,0.6,0.8,1 S/m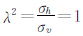 =1,1.5,2.0,2.5,3.0;第二组参数:σh=1,2,4,6,8,10 S/m,
=1,1.5,2.0,2.5,3.0;第二组参数:σh=1,2,4,6,8,10 S/m,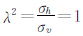 =1,2,3,4,5利用这两组数据计算的地层各向异性指数因子图板见图 1、图 2,由图可见地层水平电导率对图版的影响是非常大的,当地层水平电导率变小时曲线变的密集,这对利用图版法确定地层指数因子会造成一定的误差,因此在处理低导地层时应适当选择小间隔(水平电导率间隔变小)的图板.
=1,2,3,4,5利用这两组数据计算的地层各向异性指数因子图板见图 1、图 2,由图可见地层水平电导率对图版的影响是非常大的,当地层水平电导率变小时曲线变的密集,这对利用图版法确定地层指数因子会造成一定的误差,因此在处理低导地层时应适当选择小间隔(水平电导率间隔变小)的图板.
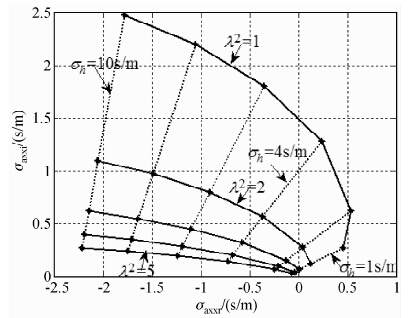 | 图 1 地层各向异性指数因子图版 Fig. 1 Chart of formation anisotropic index factor |
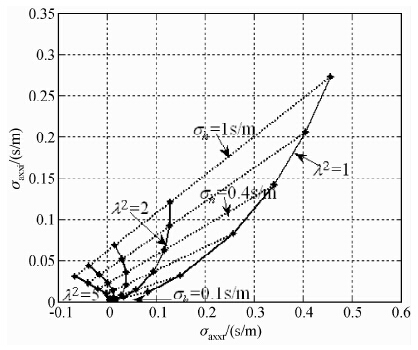 | 图 2 地层各向异性指数因子图版 Fig. 2 Chart of formation anisotropic index factor |
若有地层视电导率σaxx的实部和虚部测井资料,则可以确定地层各项异性指数因子,图版使用方法如下:
(1)根据测井仪器、测井条件、测量的范围选择针对性的三份量感应测井地层各向异性指数因子图版(如图 1,图 2等,还可以多制作一些图版,供选择使用);
(2)根据视电导率曲线得到地层视电导率实部和虚部数据σaxxr和σaxxi;
(3)利用地层视电导率实部和虚部测井数据σaxxr和σaxxi,找到图版(图 1,或图 2等)中的对应曲线上的点,根据该点所在的位置,找到离该点最近的曲线,根据曲线所标数值可大体确定地层的水平电导率与地层各项异性指数因子,再根据该点与周边曲线的距离关系利用插值法估算出地层的水平电导率与地层各项异性指数因子.
2.3 图版使用示例
下面通过模型算例说明确定地层各向异性指数因子的方法,模型计算参数与图 1的作图参数相同,再取λ2=2,σh=3,9 S/m,则x-方向发射线圈发射,x-方向线圈接收计算的数据视电导率实部为σaxxr=-0.3632,-1.7719,虚部为σaxxi= 0.5692,1.0454.由这些数据利用上面的作图方法,在图 1中绘制的点如图 3中的A、B点,由曲线知A、B点均实落在了λ2=2的曲线上(即地层各向异性指数因子为λ2=2),从而确定了地层各向异性指数因子,并且与地层模型的地层各向异性指数因子数值也取得了很好的一致.
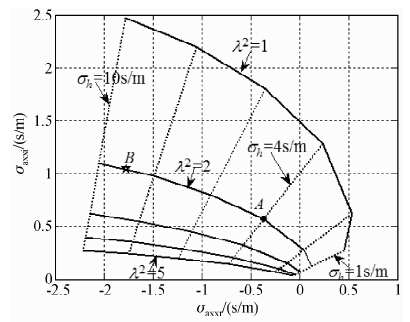 | 图 3 确定地层各向异性指数因子示例 Fig. 3 Example of the anisotropic formation index factor determined |
3.1 各向异性地层指数因子的迭代计算方法
为简化表示设ξ=L/δh,则(5)式可写为
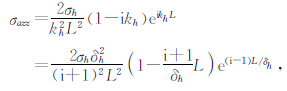
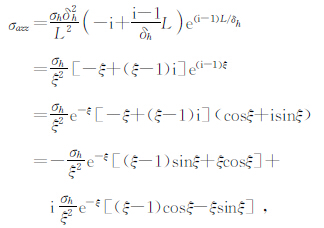
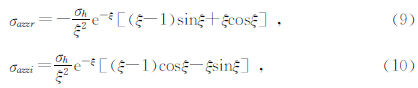

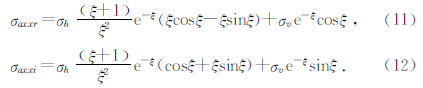
若有地层视电导率σaxx或地层视电导率σazz的实部和虚部资料则可以利用(9)~(12)中的任意两个方程就可确定地层各向异性指数因子.因(9)~(12)任意组合都为一非线性很强的方程组,只能用非线性方程组的方法求解,本文用牛顿迭代方法计算地层各向异性指数因子,将方程(11)和(12)写为σh和σv的形式得
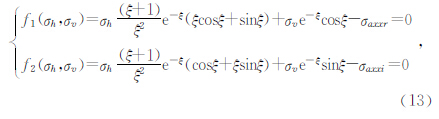
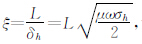 设方程(13)的第n次牛顿迭代近似解为ηn(σh,n,σv,n)(牛顿迭代解法),则方程(13)式的雅可比行列式为
设方程(13)的第n次牛顿迭代近似解为ηn(σh,n,σv,n)(牛顿迭代解法),则方程(13)式的雅可比行列式为

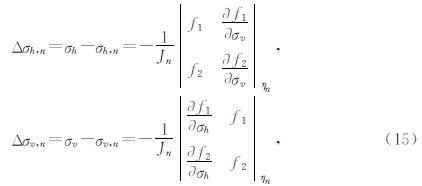
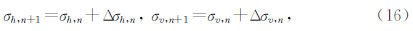
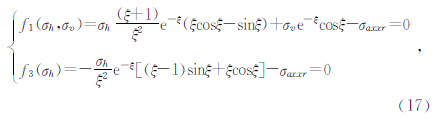

 计算λ,实现地层各向异性指数因子的计算.
3.2 地层各向异性地层指数因子算例
计算λ,实现地层各向异性指数因子的计算.
3.2 地层各向异性地层指数因子算例
为检验方法的可行性及可靠性,下面利用上面的仪器参数(与地层各向异性指数因子图版制作参数相同)、视电导率公式和地层各向异性指数因子迭代计算方法,分别计算地层电导率的实部、地层的水平电导率及地层各向异性指数因子.
现选λ2= σh σv =1,2,3,4,5,则地层的视电导率随地层电导率的变化曲线见图 4,随地层水平电导率的增大,地层视电导率呈非线性变化.
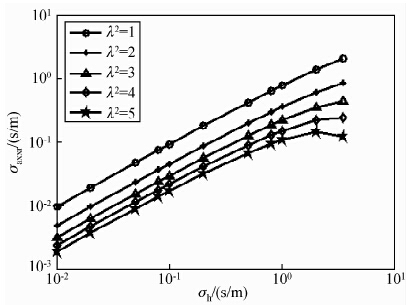 | 图 4 地层视电导率随地层真电导率的变化 Fig. 4 Variation of apparent conductivity with the formation conductivity |
利用地层视电导率σaxx的实部和虚部数据,由(13)~(16)式计算了地层各项异性指数因子(见表 1),在表 1中,λ2为地层模型的地层各项异性指数因子,λ2c为利用本迭代计算方法计算的地层各项异性指数因子,地层模型与迭代计算结果的四位有效数字是相同的,从而验证了方法的可靠性.
|
|
表 1 地层模型与迭代计算的地层各向异性指数因子结果比较 Table 1 Comparison of the computing formation anisotropy index factor and that of formation model |
利用地层视电导率σaxx的实部和虚部数据,由迭代法计算的水平水平电导率见表 2,其中,σh为地层模型的水平电导率,σhc为利用本迭代计算方法计算的水平电导率,计算结算与地层模型取得了很好的一致,进一步验证了方法的可靠性.
|
|
表 2 地层模型与迭代计算的地层水平电导率结果比较 Table 2 Comparison of computing horizontal conductivities and that of formation model |
图版法简单,使用方便,在有地层视电导率σaxx的实部和虚部资料的情况下则可以简捷地确定地层各向异性指数因子.但其缺点是 需要根据实际测井仪器、测井条件、测量范围制作多个三份量感应测井地层各向异性指数因子图版,并且当地层视电导率实部和虚部测井数据σaxxr和σaxxi不能落在图版的曲线上时,则需要根据所数据点的位置与周边曲线的距离关系利用插值法估算出地层的水平电导率与地层各向异性指数因子,这会给估算结果带来较大的误差,特别是当电导率数值较小的时候,图版曲线变化较大,会引起更大的误差.
迭代计算方法准确,算例利用地层视电导率σaxx的实部和虚部数据计算的水平电导率及地层各向异性指数因子取得了四位有效数字相同的结果,展示了计算方法的可靠性; 同时使用范围广,不受限制,不象图版法需要根据测井仪器、测井条件、测量范围事先制作多个地层各向异性指数因子图版;所需要的地层视电导率数据量少. 其缺点是计算方法具有一定的复杂度,需要求解非线性方程组,需要开发相应的迭代计算程序.
两种方法各有自己的优势与不足,这需要根据实际需要加以取舍,选择合适的方法,但就总体而言迭代计算方法以其准确与使用范围广等特点则具有更大的优势.
5 结 论
5.1 利用三维感应测井分量视电导率确定地层各向异性指数因子的计算与确定方法是一种新的确定地层各向异性指数因子的方法,该方法计算速度快,精度高. 5.2 论文介绍了地层各向异性指数因子的图板制作及确定方法;导出了地层视电导率偏导方程,实现了地层各向异性指数因子的数值计算,比较了两种算法各自的优势与不足.针对迭代计算方法给出了数值算例,算例结果表明利用地层视电导率的实部和虚部数据,计算的水平电导率及地层各向异性指数因子与地层模型取得了四位有效数字相同的结果,两者取得了很好的一致,验证了方法的可靠性,为地层各向异性指数因子的确定与测井资料解释提供了理论依据和计算方法. 致 谢 感谢审稿专家对论文提出的宝贵修改意见. 附录A 雅可比矩阵元的偏导数
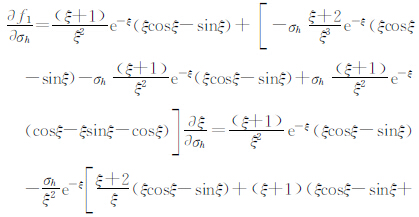



| [1] | Davydycheva S, Druskin V, Habashy T. 2003. An efficient finite-difference scheme for electromagnetic logging in 3D anisotropic inhomogeneous media[J]. Geophysics, 68(5): 1525-1536. |
| [2] | Gao L, Gianzero S, Kennedy D, et al. 2002. The response of a triaxial induction sonde in a biaxial anisotropic medium[J]. Petrophysics, 43(3): 172-183. |
| [3] | Hong D C, Xiao J Q, Zhang G Y, et al. 2013. Fast inverse the relative dip using cross-component in highly deviated well[J]. Chinese J. Geophys. (in Chinese), 56(7): 2494-2501, doi: 10.6038/cjg20130735. |
| [4] | Hungerford E T, Fay C H. 1957. Electromagnetic earth surveying apparatus[P]. US patent 3014177. |
| [5] | Klein J D, Martin P R. 1997. The petrophysics of electrically anisotropic reservoirs[J]. The Log Analyst, 38(3): 25-36. |
| [6] | Kunz K S, Moran J H. 1958. Some effects of formation anisotropy on resistivity measurements in boreholes[J]. Geophysics, 23(4): 770-794. |
| [7] | Moran J H, Kunz K S. 1962. Basic theory of induction logging and application to study of two-coil sondes[J]. Geophysics, 27(6): 829-858. |
| [8] | Moran J H, Gianzero S. 1979. Effects of formation anisotropy on resistivity-loggingmeasurements[J]. Geophysics, 44(7): 1266-1286. |
| [9] | Nam M J, Pardo D, Torres-Verdín C. 2010. Simulation of triaxial induction measurements in dipping, invaded, and anisotropic formations using a Fourier series expansion in a nonorthogonal system of coordinates and a self-adaptive hp finite-element method[J]. Geophysics, 75(3): 83-95. |
| [10] | Nekut A G. 1994. Anisotropy induction logging[J]. Geophysics, 59(3): 345-350. |
| [11] | Wang C X, Chu Z T, Xiao C W, et al. 2013. The analysis of effect of the borehole environment on responses of array induction logging[J]. Chinese J. Geophys. (in Chinese), 56(4): 1392-1403. doi: 10.6038/cjg20130433. |
| [12] | Wang H M, Barber T, Morriss C, et al. 2006. Determining anisotropic formation resistivity at any relative dip using a multiarray triaxial induction tool[C].// SPE Annual Technical Conference and Exhibition. |
| [13] | Wang H N, Tao H G, Yao J J, et al. 2008. Study on the response of a multicomponent induction logging tool in deviated and layered anisotropic formations by using numerical mode matching method[J]. Chinese J. Geophys. (in Chinese), 51(5): 1591-1599. |
| [14] | Wang H N, Hu P, Tao H G, et al. 2012. Fast algorithm of response of array multicomponent inducting logging tool in horizontally stratified inhomogeneous TI media[J]. Chinese J. Geophys. (in Chinese), 55(2): 717-726, doi: 10.6038/j.issn.0001-5733.2012.02.036. |
| [15] | Wang T, Fang S. 2001. 3-D electromagnetic anisotropy modeling using finite differences[J]. Geophysics, 66(5): 1386-1398. |
| [16] | Wang T, Yu L M, Fanini O. 2003. Multicomponent induction response in a borehole environment[J]. Geophysics, 68(5): 1510-1518. |
| [17] | Xiao J Q, Zhang G Y, Hong D C, et al. 2013. Fast forward modeling and data processing of 3D induction logging tool in layered anisotropic formation[J]. Chinese J. Geophys. (in Chinese), 56(2): 696-706, doi: 10.6038/j.issn.0001-5733.2012.06.036. |
| [18] | Yu Y M, Xiao J Q, Ke S H. 2013. On the Nummerical Modeling of 3D Induction Logging Response Calibration by FEM[J]. Well Logging Technology (in Chinese), 37(6): 613-618. |
| [19] | Zhang G Y, Xiao J Q, Hao Y J. 2012. Numerical computation and theoretical analysis of Three-dimensional induction logging tool[J]. Well Logging Technology (in Chinese), 2012, 36(1): 15-19. |
| [20] | Zhang Y, Wang H N, Tao H G, et al, 2012. Finite volume algorithm to simulate 3D response of multi-component induction of inhomogeneous anisotropic formation based on coupled-vector scalar potentials[J]. Chinese J. Geophys. (in Chinese), 55 (6): 2141-2152. doi: 10.6038/j.issn.0001-5733.2012.06.036. |
| [21] | Zhdanov M, Kennedy D, Peksen E. 2001. Foundations of Tensor Induction[J]. Well-Logging[J]. Petrophysics, 42(6): 588-610. |
| [22] | 党瑞荣, 秦瑶, 谢雁等. 2006. 三分量感应测井系统研究[J]. 石油地球物理勘探, 41(4): 484-488. |
| [23] | 洪德成, 肖加奇, 张国艳,等. 2013. 大斜度井中利用交叉分量快速反演井斜角[J]. 地球物理学报, 56(7): 2494-2501, doi: 10.6038/cjg20130735. |
| [24] | 王昌学, 储昭坦, 肖承文,等. 2013. 井环境对阵列感应测井响应的影响分析[J]. 地球物理学报, 56( 4): 1392-1403. doi: 10.6038/cjg20130433. |
| [25] | 汪宏年, 陶宏根, 姚敬金,等. 2008. 用模式匹配算法研究层状各向异性倾斜地层中多分量感应测井响应[J]. 地球物理学报, 51(5): 1591-1599. |
| [26] | 汪宏年, 胡萍, 陶宏根,等. 2012. 水平层状非均质横向同性地层中阵列多分量感应测井响应的快速计算[J]. 地球物理学报, 55(2): 717-726, doi: 10.6038/j.issn.0001-5733.2012.02.036. |
| [27] | 肖加奇, 张国艳, 洪德成,等. 2013. 层状各向异性地层中三维感应测井响应快速计算及资料处理[J]. 地球物理学报, 56(2): 696-706, doi: 10.6038/cjg20130234. |
| [28] | 俞燕明, 肖加奇, 柯式镇,等. 2013. 三维感应测井仪器刻度响应有限元法数值模拟研究[J]. 测井技术, 37(6): 613-618. |
| [29] | 张国艳, 肖加奇, 郝永杰. 2012. 三维感应测井数值计算与理论分析[J]. 测井技术, 36(1): 15-19. |
| [30] | 张烨, 汪宏年, 陶宏根,等. 2012. 基于耦合标势与矢势的有限体积法模拟非均匀各向异性地层中多分量感应测井三维响应[J]. 地球物理学报, 55(6): 2141-2152. doi: 10.6038/j.issn.0001-5733.2012.06.036. |
 2015, Vol. 30
2015, Vol. 30


