地震偏移成像是通过数学的手段将地表或井中观测到的地震数据反传播,消除地震波的传播效应得到地下结构图像的过程.一般来说,深度偏移方法主要分为两大类:射线类偏移方法和波动方程偏移方法.传统的射线类偏移方法利用几何射线理论来计算波场信息,从而具有较高的计算效率和灵活性,但是存在焦散区及阴影区等缺陷,且不能对多次波至进行成像;波动方程偏移方法以波动方程数值解法为基础,通过递归波场进行成像,因此具有更高的成像精度,但有计算效率低下的缺点(李振春,2011).结合这两种方法的优缺点,Hill(1990)提出了一种叠前Kirchhoff偏移方法和波动方程偏移方法的折中方法——高斯束偏移,高斯束方法克服了传统射线方法的缺陷和不足,使用动力学射线追踪,使波场不存在奇异性区域;另外高斯束具有一定的有效宽度,可以选择对计算点有贡献的高斯束的叠加来计算最终的波场,无需费时的两点射线追踪,大大地提高了计算效率.因此,高斯束偏移是一种兼顾效率和精度的成像方法.
高斯束法是一种将波动方程与射线方法紧密结合起来的方法.早在 20 世纪 80 年代,Červený等(Červený,1982; Červený,1983; Červenýand PšenČik,1983; Červený,1985a,1985b,2005)将电磁学领域的高斯射线束方法引入地球物理领域,提出了通过求解波动方程的高频近似解求取高斯束的方法,并成功应用到波场正演中.自从Raz(1987)提出束叠加的方法,高斯束开始在地震偏移成像领域得到了进一步研究和应用.Hill(1990)提出了叠后高斯束偏移,通过局部倾斜叠加得到局部平面波,然后通过高斯束将局部平面波分量反传至地下进行成像.Hill(2001)利用最速下降法将多重积分进行降维处理,提出了适用于共偏移距、共方位角道集的叠前高斯束偏移方法.Nowack等(2003)和Gray(2005)分别针对上述方法对观测系统适应性的不足,提出了共炮域的高斯束叠前偏移方法.
传统的高斯束偏移忽略了对其的保幅处理,Albertin等(2004)首先提出了共偏移距、窄方位角道集的保幅高斯束偏移.然而,该方法同样缺乏对观测系统的适应性,并且权函数中的Beylkin行列式(张平平和常旭,2006)太过复杂,在三维情况下难以实现.Gray and Bleistein(2009)基于Bleistein等(2005)的保幅共炮域偏移理论,将传统的高斯束偏移同保幅波动方程偏移理论相结合,提出了适用于共炮域的保幅高斯束偏移方法.杨继东等(2014)基于在考虑海拔、角度的情况下的有效邻域内的波场近似实现起伏地表保幅高斯束偏移.Popov等(2010)提出了一种以Kirchhoff积分为基础,利用高斯束的叠加积分来计算格林函数的高斯束逆时偏移算法.毕立飞等(2015)将弹性波逆时偏移和高斯束叠前偏移相结合实现了弹性多波高斯束逆时偏移.岳玉波(2011)提出了一种适用于起伏地表条件的高斯束偏移方法——保幅延拓法,同时,他和徐少波等(2014)还结合弹性动力学高斯束以及弹性波Kirchhoff积分提出了一种基于矢量波场延拓的弹性波高斯束偏移.区别于传统的高斯束偏移,黄建平等(2015)提出了双复杂条件下弹性波非倾斜叠加束偏移,证明该方法由于消除误差影响成像更精准.在各向异性介质中,也有一些学者对高斯束方法进行了研究与发展.Červen(1972)给出了一个高效的非均匀各向异性介质射线追踪系统,Hanyga(1986) 给出了各向异性介质中的动力学射线追踪方程组,Alkhalifah(1995)实现了各向异性介质中高斯束偏移.段鹏飞等(2013b,2014)采用相速度表征运动学和动力学射线方程组并通过一些各向异性高斯束近似方案实现了各项异性介质中角度域叠前高斯束偏移,同时给出高斯束角度域共成像点道集的提取方法.近年来,为了达到更精确更快速的目的,一些其他的束方法也得到了发展应用,如控制束、快速射线束、聚焦束、投影菲涅尔束等.
本文以高斯束为研究对象,系统地介绍了不同类型的高斯束偏移成像方法包括叠后偏移、叠前偏移、起伏地表高斯束偏移、高斯束逆时偏移、弹性波高斯束偏移、各向异性介质高斯束偏移以及其他束方法的简介和计算中的一些优化策略问题,并对高斯束偏移方法下一步发展方向进行了初步展望. 1 高斯束偏移方法
1.1 高斯束叠后偏移
高斯束叠后偏移是由Hill(1990)提出的,高斯束偏移中关键一点是格林函数的表示方法:将接收点处的格林函数由附近的束中心出射的高斯束的叠加积分来表示,即
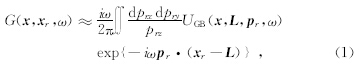
为了减小当接收点与束中心距离较远时产生的误差,对地表观测排列加入一系列重叠的高斯窗,根据RayleighII积分公式得到基于高斯束表示的反向延拓波场:
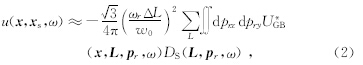
叠后偏移采用爆炸反射面成像条件(Claerbout,1985),得到最终的叠后偏移公式为
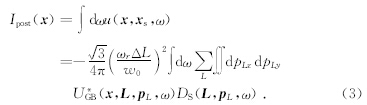
高斯束叠后偏移的实现过程可以大体表示为:(1)根据束中心间隔,确定一系列束中心的位置;(2)对于每个束中心位置,将其有效范围内的地震记录进行倾斜叠加,分解为不同方向局部平面波;(3)在束中心位置根据平面波的初始方向试射高斯束,然后根据高斯束的走时以及振幅信息进行成像.
1.2 高斯束叠前偏移
根据Clayton等和Hildebrand等(Clayton and Stolt,1981; Hildebrand and Carroll,1993)所提出的波场双向延拓积分,可以将高斯束叠前成像公式表示为
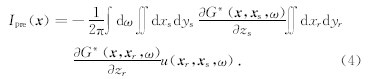
叠前偏移既可以在炮点、接收点域进行,也可以转换到中心点、偏移距域中进行.但是直接计算需要耗费巨大的计算量,同样可以利用束中心出射的高斯束的叠加来近似计算附近接收点的格林函数来减少计算量.选择不同域进行上述过程,便可以得到不同道集的偏移公式(岳玉波,2011).
Hill(2001)实现了共偏移距、共方位角道集的高斯束叠前偏移,但不能很好的适应观测系统,Gray(2005)将高斯束叠前偏移应用到共炮域数据中.类似于Hill的方法,首先对共炮数据根据接收点射线参数进行局部倾斜叠加,然后根据炮点射线参数进行地下点的成像.但是这样的方法会降低成像精度,因为它不能解决炮点射线多路径的问题,为了提高精度,可以在成像过程中将炮点、接收点射线参数转化为中心点、偏移距射线参数,修改后偏移流程可以表示为:
对每个接收点束中心位置{
加窗倾斜叠加并计算由炮点和接收点试射的高斯束
对每个中心点射线参数{
对每个粗网格成像点{
扫描偏移距射线参数并得到虚部时间最小时的值
}粗网格成像点循环结束
对偏移孔径内每个成像点{
根据扫描得到的走时、振幅信息对所对应的倾斜叠加道进行成像
}成像点循环结束
}中心点射线参数循环结束
}接收点束中心循环结束
国内的公司和学者在叠前高斯束的研究和应用方面也做了大量工作.王志亮等(2011)将高斯束偏移方法运用到渤海LD16-17区,通过对同一速度模型高斯束偏移和Kirchhoff偏移的结果对比得出高斯束偏移的信噪比更高、断层更加清晰,中深层成像能量更强.蔡杰雄等(2012)系统的介绍了高斯束偏移方法的实现过程,从射线中心坐标系得到高斯束公式出发,按照运动学射线追踪、动力学射线追踪及高斯束偏移三部分实现叠后、叠前和起伏地表高斯束偏移.谢飞等(2013)不仅推导了叠前偏移的频率域计算公式且根据Hale方法介绍了时间域的实现方法,由于高斯束方法携带方向信息,其还给出了角度域共成像点道集的计算方法.
1.3 起伏地表高斯束偏移
射线类偏移成像方法易于适用复杂地表条件.Kirchhoff偏移可以直接在起伏地表进行波场的延拓和成像.Gray和Marfurt(1995)证明直接在复杂地表进行Kirchhoff偏移效果要优于先进行基准面校正然后进行偏移的结果.Jager等(2003)给出了起伏地表条件下的保幅Kirchhoff偏移方法.
作为Kirchhoff偏移方法的替代方法,Gray(2005)提出了一种适应于复杂地表条件的高斯束偏移方法——局部静校正法,其基本思路是:通过简单的高程校正将同一个高斯窗内接收点的高程校正到束中心所在的基准面上,然后在此基准面上进行局部平面波的分解以及成像.但是当地表起伏变化剧烈时,直接进行高程校正会对最终偏移结果造成不利影响.针对上述问题,岳玉波(2011)提出了一种新的方法——保幅延拓法,保幅延拓法直接在起伏地表进行局部倾斜叠加,具有更好的成像效果.
保幅延拓法得到的基于高斯束表示的复杂地表波场反向延拓公式为
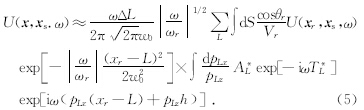
不同于常规的高斯束叠前偏移,其包含了起伏地表的高程以及倾角信息,直接在起伏地表表面进行局部平面波的分解.当近地表起伏剧烈变化时,可以通过计算上式中的相移量exp[iω(pLx(xr-L)+pLzh)来提高局部平面波分解的精度.
曹文俊等(2013)将该方法应用到山前带地区实际资料,证明了高斯束偏移方法可以很好地适用于地表起伏情况,且波组特征明显,便于层位解释.
1.4 高斯束逆时偏移
所谓逆时偏移,就是对地震记录在时间方向上进行反向外推并储存地下每个成像点不同时刻的成像值,然后利用成像条件进行成像的一种具有极高成像精度的偏移方法.常规的逆时偏移算法都是基于双程波动方程的数值解法(张春燕等,2010),实际上利用Kirchhoff积分进行波场延拓,也可以实现逆时偏移.Popov等(2010)提出了一种以Kirchhoff积分为基础,利用高斯束的叠加积分来计算格林函数的逆时偏移算法.该方法同常规Kirchhoff积分偏移以及高斯束偏移相比,有更高的成像精度,同常规的逆时偏移相比,具有更高的计算效率,并且具有面向目标的成像的能力.黄建平等(2014)实现了基于格林函数求和的声波高斯束逆时偏移方法,并通过实际资料计算,验证了方法一定的适应性和成像优势.
1.5 弹性波高斯束偏移
基于矢量波场延拓的弹性波偏移成像方法主要分为两大类:一类是弹性波逆时偏移,其将多分量地震数据作为边界条件进行逆时外推,然后利用互相关成像条件求取成像值. Chang和McMechan(1994),Botelho和Stoffa(1991),Yan和Sava(2008)以及杜启振和秦童(2009)分别将弹性波逆时偏移延伸到三维和各向异性介质中.另一类是弹性波Kirchhoff偏移,通过计算本型波以及转换波的走时、振幅信息,沿所选择波型的走时轨迹叠加进行成像.Kuo和Dai(1984)首先提出了该方法,此后,Sena和Toksoz(1993),Hokstad(2000)以及Druzhinin(2003)对其进行了发展.上述两种方法,具有各自的优势及不足,其中弹性波逆时偏移虽然具有很高的成像精度,但其计算量非常大,而且其成像结果往往伴有低频噪音以及转换波成像时的极性反转问题.弹性波Kirchhoff偏移,虽然具有计算效率高的特点,但是其难以对多次波至进行成像,致使其成像精度不高.
针对上述方法存在的不足,岳玉波(2011)提出了一种同时具有较高成像精度以及计算效率的弹性波成像方法——弹性波高斯束偏移.由于高斯束可以自然地对多次波至进行成像,因此比Kirchhoff偏移具有更高的成像精度;另外,通过局部倾斜叠加进行平面波分解并利用对应的高斯束进行延拓成像,又使得该方法具有远高于逆时偏移的计算效率.
首先从二维弹性波Kirchhoff-Helmholtz积分出发,利用弹性动力学高斯束来表示位移格林张量,推导了解耦的弹性波波场反向延拓公式为
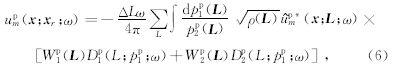
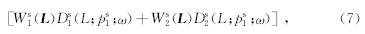
然后利用互相关成像条件来求取反射波以及转换波的成像值.
在对转换波进行成像时,往往出现转换波偏振方向不同而导致的成像剖面中的极性反转现象,严重影响叠加成像的效果.分析得到X分量记录中转换S波的极性同P波入射角的正负有关,因此可以根据P波入射角的正负直接对成像结果进行校正,为此引入符号函数,将P-S成像公式改写为
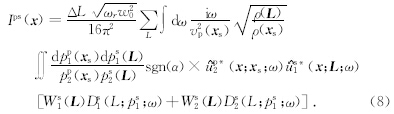
1.6 各向异性高斯束偏移
一些学者对高斯束算法在各向异性介质中的应用也进行了研究,在各向同性介质高斯束偏移算法的基础上,修改射线追踪方程组和动力学方程组,实现各向异性介质中的高斯束偏移算法.
Červený(1972)推导了一个高效的非均匀各向异性介质的射线追踪方程,它是基于解Christoffel矩阵Γ特征值的偏微分方程而不是直接解特征值本身.
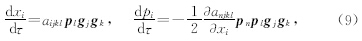
Hanyga(1986)给出了各向异性介质中的动力学射线追踪方程组
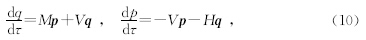
Alkhalifah(1995)证明其在各向异性叠后高斯束偏移方法中改变两个追踪方程组额外的计算成本很低,段新意等(2014)也证明了该方法的正确性和高效性.
段鹏飞等(2013a)提出两种改进的射线追踪方法:由相速度表征的射线追踪方程和VTI介质声学近似下的射线追踪方程.后来他们采用改进的相速度表征的方法分别求取运动学和动力学射线方程组,并且将动力学射线方程组变换到在各向异性介质中依然正交的波前正交坐标系中,实现TI介质局部域论框架下的高斯束叠前深度偏移方法(段鹏飞等,2013b).
1.7 其它束方法
随着勘探难度的增大,对成像方法的要求也越来越高,比如:更好的成像精度和更快的计算效率.一些以高斯束为基础的延伸的其他束方法也得到了发展和应用,如:controlled beam、focused beam、fast beam、complex beam等.
CGGVeritas一直在研究和使用束偏移方法并且将其广泛应用于复杂地区成像(Gray et al,2002; Roberts et al.,2008).随着对于该方法的进一步研究,得到了一种更为行之有效的方法,被称为controlled beam.控制束选择tau-p域内满足条件的成像点进行成像.Vetle Vinje等通过一系列的实例包括原有数据的再处理,复杂叠前深度偏移模型的建立和对最近的宽方位角数据成像,阐述了CBM的优点(Sun et al.,2007; Vinje et al.,2008).CGG公司将控制束方法应用于墨西哥湾、北海北部等区域证明了控制束方法的正确性和有效性(Ting and Wang,2008,2009; Brahim et al.,2009),后来又发展了各向异性介质和转换波控制束偏移(Zhou et al.,2011; Casasanta and Grion,2012; Casasanta et al.,2013).目前CBM已经被广泛应用于速度模型的建立,构造成像以及对数据稀疏、信噪比较低的数据的成像.
高富春等(2006,2007)最早提出fast beam并实现二维介质中快速束偏移之后又拓展到三维.其基本思想就是:在对记录数据进行筛选后,利用高斯束偏移的方法进行射线追踪并通过子波映射完成的偏移,因此不仅解决了多路径成像的问题也大大提高了计算效率.此外,Mo等(2009)和Alex and er等(2013)分别基于kirchhoff偏移和平面波的构造的思想,提出了其他快速束深度偏移实现算法方法.虽然目前快速束实现算法各种各样,但主要思想还是在高斯束偏移的格架上吸收其他偏移方法、信号处理的实用技术,来提高计算的速度个偏移的精度.
聚焦束成像方法源于Ceveny(1985)所提出高斯束在反射界面深度聚焦的思想,即选用特殊的初始参数使得高斯束的束腰位于地下反射点处.Nowack(2008)首先将其应用于高斯束成像中,提出了了具有单一聚焦深度的聚焦束成像方法,之后又根据散射的思想发展了动态聚焦束偏移,即将束腰置于地下每个散射点上,提高了常规高斯束偏移的精度(Nowack,2011).
Complex beam migration由CGG 的Zhu(2013)提出,该束方法主要用于复杂地形、地表起伏较大的区域.从波动方程的Maslov解出发求取Complex-beam的表达式,然后通过Complex-beam的叠加得到波场值,既保留了Kirchhoff偏移的灵活性,又能对多次波至进行成像.Tianfei Zhu通过对陆地数据的成像发现Complex beam比高斯束偏移更稳定并且对复杂区域的成像更准确.
2 高斯束的方法优化
当今计算机硬件技术的迅速发展使得三维叠前深度偏移正在逐步走向实用,但是其庞大的计算量依然是亟待解决的难题.在种类繁多,各具特点的叠前深度偏移方法中(张钋等,2000;赵连功和刘洪,2003;罗银河等,2004;张丽艳和刘洋,2005;马淑芳和李振春,2007),高斯束偏移是一种非常适用于三维叠前深度域成像的偏移方法,一方面,其具有很高的计算效率;另一方面,它也具有接近于波动方程偏移的成像效果.
在射线类偏移方法的编程实现过程中,优化算法、参数选择以及成像条件优化往往是提高效率和改善成像精度的关键(李振春等,2003;程玖兵等,2005;李博等,2009).
2.1 最近点搜索算法
在高斯束的求解过程中,需要确定地下网格点在射线中心坐标系中的位置来计算该点的波场值.Hale(1992a,1992b)依据下述特点: x点对应最近射线点,往往在x 邻近规则网格点所对应最近射线点的附近,给出了一种优化算法.
首先,将N个离散的射线路径点划分为Nc组,每组中近似含有N/Nc个射线路径点(如图 1所示);接下来,当求 x点的最近射线点时,首先选择一个圆环(最好选择一个此前搜索到的x邻近网格点对应的最近射线点所在的圆环),在该圆环内搜索离x点最近的射线点,并保存最短距离;然后,对于剩余的圆环,只需要选择x 点到圆心的距离减去半径小于已知最短距离的圆环进行搜索即可,直到得到最近射线点.
 | 图 1 优化算法示意图(岳玉波,2011) Fig. 1 Sektch of optimized algorithm |
由于高斯束的走时和振幅是光滑变化的,因此可以通过在粗网格上求取信息然后再插值到细网格上的方法进行成像.粗网格的应用可以显著提高高斯束偏移的计算效率,且不会影响最后的成像质量.岳玉波进行了试算测试发现,选择较细网格稀疏10倍以内的粗网格进行程序计算,最终的成像效果不存在本质的区别(岳玉波,2011;岳玉波等,2012),并且递归算法具有数倍、甚至数十倍于循环算法的计算效率.
递归算法可以表示为:从高斯束中心射线出射点最近的网格点出发,分别求取其上、下、左、右、前、后六个粗网格点上的振幅、走时信息,然后判断其是否为有效点.若为有效点,则继续上述递归过程;若为无效点,则停止,直到求取完所有的有效网格点.
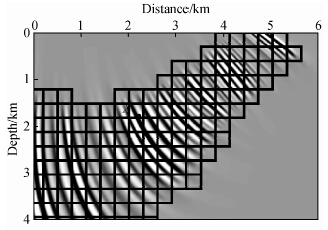 | 图 2 粗网格及递归算法示意图(岳玉波,2011) Fig. 2 Sektch of coarse gird and recursive algorithm |
高斯束叠前成像算法,可以对所有的波至进行成像,因而是非常精确的,但是其计算效率不高.Hill针对上述问题,提出了一种具有较高计算效率的高斯束偏移实现方法,其基本原理在于:偏移成像公式中的核心部分在于高斯束积分计算公式(以共炮为例)
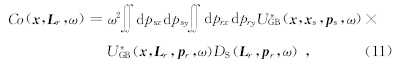

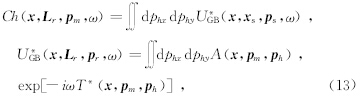
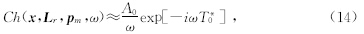
3 高斯束偏移发展方向初步展望
由于高斯束偏移方法具有易于适应不规则观测系统和复杂地表的优点,且易于向三维延伸,因此未来对高斯束偏移方法的应用会更加广泛,高斯束偏移方法的发展也会越来越快.作者认为高斯束的未来发展方向主要有以下几个方面:
(1)基于不同网格剖分策略的各向异性介质高斯束偏移研究;
(2)三维高斯束偏移被广泛应用,在成像精度和计算效率方面得到进一步完善;
(3)以高斯束为基础,以某种特殊目的为研究目的的其他束方法在实际资料的处理中得到重用,例如控制束(Sun et al.,2007; Vinje et al.,2008; Ting and Wang,2008,2009; Brahim et al.,2009; Zhou et al.,2011; Casasanta and Grion,2012; Casasanta et al.,2013)、快速束(Gao et al.,2006,2007; Popov et al.,2007; Mo et al.,2009)、聚焦束(Nowack,2008,2011)、投影菲涅尔束(Schleicher et al.,1997; Cruz et al.,2012)等偏移方法.
4 结论及讨论
高斯束偏移是一种优异的叠前深度偏移成像方法,它既保留了传统射线类处理方法运算效率高的优点,且具有接近波动方程类方法的成像精度.本文系统分析了不同类型的高斯束偏移成像方法的发展历程,主要趋势为:从叠后偏移发展到叠前偏移,从水平地表过渡到起伏地表高斯束偏移,从声波方程发展到弹性波高斯束偏移,从各向同性介质过渡到各向异性介质高斯束偏移,从常规高斯束发展到控制束、聚焦束、快速束、投影菲涅尔束偏移以及高斯束逆时偏移等.高斯束方法的适应性、成像精度等都得到了极大提高,是一种非常有发展潜力的成像方法.
近年来,随着三维勘探的不断深入,高斯束偏移方法的优势逐渐凸显,在三维实际资料处理中,高斯束偏移方法已经得到广泛应用.当然,高斯束偏移依然存在需要加以改进和完善的地方,比如对深层构造的保幅成像及三维情况下的加速处理等,需要在后续的研究过程发展基于反演思想的最小二乘高斯束偏移(黄建平等,2013a,2013b,2014),并发展相应的GPU算法(刘红伟等,2010,2011).
致 谢 感谢国家重点基础研究发展计划(973)(2014CB239006, 2011CB202402),国家自然科学基金(41104069,41274124),中央高校基本科研业务费专项基金(R1401005A)联合资助.
| [1] | Albertin U, Yingst D, Kitchenside P. 2004. True-amplitude beam migration[C]// 74th Annual International Meeting, SEG. Expanded Abstracts, 398-401. |
| [2] | Alkhalifah T. 1995. Gaussian beam depth migration for anisotropic media[J]. Geophysics, 60(5): 1474-1484. |
| [3] | Bi L F, Qin N, Yang X D, et al. 2015. Gauss beam reverse time migration method for elastic multiple wave[J]. Geophysical Prospecting for Petroleum (in Chinese), 54(1): 64-70. |
| [4] | Bleistein N, Zhang Y, Xu S, et al. 2005. Migration/inversion: Think image point coordinates, process in acquisition surface coordinates[J]. Inverse Problems, 21(5): 1715-1744. |
| [5] | Botelho M A B, Stoffa P L. 1991. Finite-difference prestack reverse-time migration using the P-Sv wave equation[C]// 61st Annual International Meeting, SEG. Expanded Abstracts, 1009-1012. |
| [6] | Brahim B, Varley S, Michaud O, et al. 2009. Application of beam migration techniques to the evaluation of an exploration prospect(balvenie): A case history from the UKCS northern north sea[C]// 71st EAGE Conference and Exhibition Incorporating, SPE. |
| [7] | Cai J X, Fang W B, Yang Q Y. 2012. Implementation and application of Gaussian beam depth migration[J]. Geophysical Prospecting for Petroleum (in Chinese), 51(5): 469-475. |
| [8] | Cao W J, Wang H Z, Li Z C, et al. 2013. Application of complex topographic Gaussian beam amplitude-preserved pre-stack depth migration in piedmont zone[J]. Progress in Geophysics (in Chinese), 28(6): 3086-3091, doi: 10.6038/pg20130633. |
| [9] | Casasanta L, Grion S. 2012. Converted-wave controlled-beam migration for vector-offset volumes[C]// 82nd Annual International Meeting, SEG. Expanded Abstracts, 1-5. |
| [10] | Casasanta L, Gray S, Grion S. 2013. Converted-wave controlled beam migration with sparse sources or receivers[C]// 75th EAGE Conference and Exhibition Incorporating, SPE. |
| [11] | Červený V. 1972. Seismic rays and ray intensities in inhomogeneous anisotropic media[J]. Geophys. J. Int., 29(1): 1-13. |
| [12] | Červený V, Hron F. 1980. The ray series method and dynamic ray tracing system for three-dimensional inhomogeneous media[J]. Bulletin of the Seismological Society of America, 70(1): 47-77. |
| [13] | Červený V. 1983. Synthetic body wave seismograms for later ally varying layered structures by the Gaussian beam method[J]. Geophys. J. Int., 73(2): 389-426. |
| [14] | Červený V, PšenČik,1983; ČI. 1983. Gaussian beams and paraxial ray approximation in three dimensional elastic inhomogeneous media[J]. J. Geophys., 53: 1-15. |
| [15] | Červený V. 1985a. Gaussian beam synthetic seismograms[J]. J. Geophys., 58: 44-72. |
| [16] | Červený V. 1985b. Ray synthetic seismograms for complex two-and three-dimensional structures[J]. J. Geophys., 58: 2-26. |
| [17] | Červený V. 2005. Seismic Ray Theory[M]. Cambridge: Cambridge University Press. |
| [18] | Chang W F, McMechan G A. 1994. 3-D elastic prestack, reverse-time depth migration[J]. Geophysics, 59(4): 597-609. |
| [19] | Cheng J B, Wang H Z, Ma Z T. 2005. Double square root equation migration methods of narrow azimuth seismic data[J]. Chinese J. Geophys. (in Chinese), 48(2): 399-405. |
| [20] | Claerbout J F. 1985. Imaging the Earth's Interior [M]. Oxford: Blackwell Scientific Publications. |
| [21] | Clayton R W, Stolt R H. 1981. A Born-WKBJ inversion method for acoustic reflection data[J]. Geophysics, 46(11): 1559-1567. |
| [22] | Cruz J C R, Lira G, Ferreira C A. 2012. Seismic modeling by Gaussian beams limited by projected Fresnel zone[C]// 74th EAGE Conference and Exhibition Incorporating, SPE. |
| [23] | Druzhinin A. 2003. Decoupled elastic prestack depth migration[J]. Journal of Applied Geophysics, 54(3-4): 369-389. |
| [24] | Du Q Z, Qin T. 2009. Multicomponent prestack reverse-time migration of elastic waves in transverse isotropic medium[J]. Chinese J. Geophys. (in Chinese), 52(3): 801-807. |
| [25] | Duan P F, Cheng J B, Chen S P, et al. 2013a. Local angle-domain ray tracing and pre-stack depth migration in TI medium[J]. Chinese J. Geophys. (in Chinese), 56(1): 269-279, doi: 10.6038/cjg20130128. |
| [26] | Duan P F, Cheng J B, Chen A P, et al. 2013b. Local angle-domain Gaussian beam pre-stack depth migration in TI medium[J]. Chinese J. Geophys. (in Chinese), 56(12): 4206-4214, doi: 10.6038/cjg20131223. |
| [27] | Duan P F, Cheng J B, He G M,et al. 2014. Local angle-domain Gaussian beam prestack depth migration in anisotropic medium[C]// CPS/SEG 2014 Beijing International Geophysical Conference and Exposition. 408-411. |
| [28] | Duan X Y, Li Z C, Huang J P, et al. 2014. A prestack Gaussian beam depth migration in common-shot domain for anisotropic media [J]. Geophysical Prospecting for Petroleum (in Chinese), 53(5): 579-586. |
| [29] | Gao F C, Zhang P, Wang B, et al. 2006. Fast beam migration-a step toward interactive imaging[C]// 76th Annual International Meeting, SEG. Expanded Abstracts, 2470-2474. |
| [30] | Gao F C, Zhang P, Wang B, et al. 2007. Interactive seismic imaging by fast beam migration[C]// 69th EAGE Conference and Exhibition Incorporating, SPE. |
| [31] | Gray A H, Marfurt K J. 1995. Migration from topography: Improving the near-surface image [J]. Canadian Journal of Exploration Geophysics, 31(1-2): 18-24. |
| [32] | Gray S H, Notfors C, Bleistein N. 2002. Imaging using multi-arrivals: Gaussian beams or multi-arrival Kirchhoff?[C]// 72nd International Meeting, SEG. Expanded Abstracts, 1117-1120. |
| [33] | Gray S H. 2005. Gaussian beam migration of common-shot records[J]. Geophysics, 70(4): S71-S77. |
| [34] | Gray S H, Bleistein N. 2009. True-amplitude Gaussian-beam migration[J]. Geophysics, 74(2): S11-S23. |
| [35] | Hale D. 1992a. Migration by the Kirchhoff, slant stack, and Gaussian beam methods[R]. Center for Wave Phenomena, Colorado School of Mines, CWP-126. |
| [36] | Hale D. 1992b. Computational aspects of Gaussian beam migration[R]. Center for Wave Phenomena, Colorado School of Mines, CWP-127. |
| [37] | Hanyga A. 1986. Gaussian beams in anisotropic elastic media[J]. Geophys. J. Int., 85(3): 473-504. |
| [38] | Hildebrand S T, Carroll R J. 1993. Radon depth migration[J]. Geophysical Prospecting, 41(2): 229-240. |
| [39] | Hill N R. 1990. Gaussian beam migration[J]. Geophysics, 55(11): 1416-1428. |
| [40] | Hill N R. 2001. Prestack Gaussian-beam depth migration[J]. Geophysics, 66(4): 1240-1250. |
| [41] | Hokstad K. 2000. Multicomponent Kirchhoff migration[J]. Geophysics, 65(3): 861-873. |
| [42] | Huang J P, Li Z C, Kong X, et al. 2013a. A study of the least-squares migration imaging method for fractured-type carbonate reservoir[J]. Chinese J. Geophys. (in Chinese), 56(5): 1716-1725, doi: 10.6038/cjg20130529. |
| [43] | Huang J P, Li Z C, Liu Y J, et al. 2013b. The least square pre-stake depth migration on complex media[J]. Progress in Geophysics (in Chinese). 28(6): 2977-2983, doi: 10.6038/pg20130619. |
| [44] | Huang J P, Cao X L, Li Z C, et al. 2014a. Least square reverse time migration in high resolution imaging of near surface[J]. Oil Geophysical Prospecting (in Chinese), 49(1): 107-112. |
| [45] | Huang J P, Zhang Q, Zhang K, et al. 2014b. Reverse time migration with Gaussian beams based on the Green function[J]. Oil Geophysical Prospecting (in Chinese), 49(1): 101-106. |
| [46] | Huang J P, Yuan M L, Li Z C, et al. 2015. An accurate elastic beam migration method without slant stack for complex surface and subsurface geological conditions[J]. Geophysical Prospecting for Petroleum (in Chinese), 54(1): 56-63. |
| [47] | Jager C, Hertweck T, Spiner M. 1999. True-amplitude Kirchhoff migration from topography[C]// 69th Annual International Meeting, SEG. Expanded Abstracts, 1239-1248. |
| [48] | Kuo J T, Dai T F. 1984. Kirchhoff elastic wave migration for the case of noncoincident source and receiver[J]. Geophysics, 49(8): 1223-1238. |
| [49] | Li B, Liu G F, Liu H. 2009. A method of using GPU to accelerate seismic pre-stack time migration[J]. Chinese J. Geophys. (in Chinese), 52(1): 245-252. |
| [50] | Li Z C, Yao Y X, Ma Z T, et al. 2003. Migration velocity modeling based on common reflection surface gather [J]. Acta Seismologica Sinica (in Chinese), 25(4): 406-414. |
| [51] | Li Z C. 2011. The Theory and Method of Seismic Prestack Migration[M]. Dongying: China University of Petroleum Press. |
| [52] | Lin Y H, Zhang Z J, Yin C, et al. 2003. Hybrid optimization of static estimation in complex topography [J]. Chinese J. Geophys. (in Chinese), 46(1): 101-106. |
| [53] | Liu H W, Li B, Liu H, et al. 2010. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation[J]. Chinese J. Geophys. (in Chinese), 53(7): 1725-1733, doi: 10.3969/j.issn.0001-5733.2010.07.024. |
| [54] | Liu H W, Liu H, Li B, et al. 2011. Pre-stack reverse time migration for rugged topography and GPU acceleration technology[J]. Chinese J. Geophys. (in Chinese), 54(7): 1883-1892, doi: 10.3969/j.issn.0001-5733.2011.07.022. |
| [55] | Luo Y H, Liu J P, Yu G Z. 2004. A review on the prestack depth migration[J]. Geophysical and Geochemical Exploration (in Chinese), 28(6): 540-545. |
| [56] | Ma S F, Li Z C. 2007. Review of wave equation prestack depth migration methods[J]. Progress in Exploration Geophysics (in Chinese), 30(3): 153-161. |
| [57] | Mo L W, Shurtleff R, David H. 2009. 3-D shot-profile Kirchhoff fast beam depth migration[C]// CPS/SEG International Geophysical Conference & Exposition. |
| [58] | Nowack R L, Sen M K, Stoffa P L. 2003. Gaussian beam migration for sparse common-shot and common-receiver data[C]// 73th Annual International Meeting, SEG. Expanded Abstracts, 1114-1117. |
| [59] | Nowack R L. 2008. Focused Gaussian beams for seismic imaging[C]// 78th Annual International Meeting, SEG. Expanded Abstracts, 2376-2380. |
| [60] | Nowack R L. 2011. Dynamically focused Gaussian beams for seismic imaging[J]. International Journal of Geophysics, 2011: Article ID 316581. |
| [61] | Popov M M, Semtchenok N, Popov P, et al. 2007. Reverse time migration with Gaussian beams and its application to a few synthetic data sets[C]// 77th Annual International Meeting, SEG. Expanded Abstracts, 2165-2169. |
| [62] | Popovici A M, Tanushev N, Sturzu I, et al. 2013. Fast beam migration using plane wave destructor (PWD) beam forming[C]// 75th EAGE Conference & Exhibition Incorporating, Society of Petroleum Engineers. |
| [63] | Raz S. 1987. Beam stacking: A generalized preprocessing technique[J]. Geophysics, 52: 1199-1210. |
| [64] | Roberts G, Leggott R, Wombell R, et al. 2008. Beam migration in the North Sea[C]// Norwegian Petroleum Society Biennial Geophysical Seminar, Kristiansand. |
| [65] | Schleicher J, Hubral P, Tygel M, et al. 1997. Minimum apertures and Fresnel zones in migration and demigration[J]. Geophysics, 62(1): 193-194. |
| [66] | Sena A G, Toksoz M N. 1993. Kirchhoff migration and velocity analysis for converted and nonconverted waves in anisotropic media[J]. Geophysics, 58(2): 265-276. |
| [67] | Sun J, Don P, Sun J, et al. 2007. Imaging of fractures and faults inside granite basement using controlled beam migration[C]// 19th International Geophysical Conference & Exhibition, ASEG. |
| [68] | Ting C O, Wang D L. 2008. Controlled beam migration applications in Gulf of Mexico[C]// 78th Annual International Meeting, SEG. Expanded Abstracts, 368-372. |
| [69] | Ting C O, Wang D L. 2009. Controlled beam migration: Application in Gulf of Mexico[C]// 11th International Congress of the Brazilian Geophysical Society. |
| [70] | Vinje V, Roberts G, Taylor R. 2008. Controlled beam migration: a versatile structural imaging tool[C]// ASEG. First Break, 26(7), 109-113. |
| [71] | Wang Z L, Zhou B, Gao Q, et al. 2011. An application of Gaussian beam migration to Block LD16-17 in Bohai Sea[J]. China Offshore Oil and Gas (in Chinese), 23(5): 307-308. |
| [72] | Xie F, Li P, Huang Z Y, et al. 2013. Study of Gaussian beam pre-stack depth migration[J]. Geophysical Prospecting for Petroleum (in Chinese), 52(1): 65-71. |
| [73] | Xu S B, Yue Y B, Wang S J. Elastic Gaussian beam pre-stack depth migration[J]. Oil Geophysical Prospecting (in Chinese), 49(2): 259-265, 287. |
| [74] | Yan J, Sava P. 2008. Isotropic angle-domain elastic reverse-time migration[J]. Geophysics, 73(6): S229-S239. |
| [75] | Yang J D, Huang J P, Wang X, et al. 2014. Amplitude-preserved Gaussian beam migration based on wave field approximation in effective vicinity under rugged topography condition[C]// 84th Annual International Meeting, SEG. Expanded Abstracts, 3852-3856. |
| [76] | Yue Y B. 2011. Study on Gaussian beam migration methods in complex medium[D]. QingDao: China University of Petroleum (East China). |
| [77] | Yue Y B, Li Z C, Qian X Z, et al. 2012. Amplititude-preserved Gaussian beam migration under complex topographic conditions[J]. Chinese J. Geophys. (in Chinese), 55(4): 1376-1383, doi: 10.6038/j.issn.0001-5733.2012.04.033. |
| [78] | Zhang C Y, Li Z C, Sun X D. 2010. The review of reverse-time migration [J]. Progress in Exploration Geophysics (in Chinese), 33(5): 309-317. |
| [79] | Zhang L Y, Liu Y. 2005. Overview of prestack time migration for converted wave[J]. Progress in Geophysics (in Chinese), 20(4): 1134-1139. |
| [80] | Zhang P, Li Y M, Liu H. 2000. The situation of several prestack depth migration methods[J]. Progress in Geophysics (in Chinese), 15(2): 30-39. |
| [81] | Zhang P P, Chang X. 2006. The weight functions of amplititude-preserving migration[J]. Progress in Geophysics (in Chinese), 21(1): 203-207. |
| [82] | Zhao L G, Liu H. 2003. The research situation and trend of development of the seismic exploration processing software[J]. Progress in Geophysics (in Chinese), 18(4): 598-601. |
| [83] | Zhou B, Zhou J, Wang Z L, et al. 2011. Anisotropic depth imaging with high fidelity controlled beam migration: A case study in Bohai, offshore China[C]// 81st Annual International Meeting, SEG. Expanded Abstracts, 217-221. |
| [84] | Zhu T F. 2013. Complex-beam migration: Formulation and comparisons[C]// 83th Annual International Meeting, SEG. Expanded Abstracts, 3687-3691. |
| [85] | 毕立飞, 秦宁, 杨晓东,等. 2015. 弹性多波高斯束逆时偏移方法[J]. 石油物探, 54(1): 64-70. |
| [86] | 蔡杰雄, 方伍宝, 杨勤勇. 2012. 高斯束深度偏移的实现与应用研究[J]. 石油物探, 51(5): 469-475. |
| [87] | 曹文俊, 王华忠, 李振春,等. 2013. 复杂地表高斯束保幅叠前深度偏移在山前带地区的应用[J]. 地球物理学进展, 28(6): 3086-3091, doi: 10.6038/pg20130633. |
| [88] | 程玖兵, 王华忠, 马在田. 2005. 窄方位地震数据双平方根方程偏移方法探讨[J]. 地球物理学报, 48(2): 399-405. |
| [89] | 杜启振, 秦童. 2009. 横向各向同性介质弹性波多分量叠前逆时偏移[J]. 地球物理学报, 52(3): 801-807. |
| [90] | 段鹏飞, 程玖兵, 陈三平,等. 2013a. TI介质局部角度域射线追踪与叠前深度偏移成像[J]. 地球物理学报, 56(1): 269-279, doi: 10.6038/cjg20130128. |
| [91] | 段鹏飞, 程玖兵, 陈爱萍,等. 2013b. TI介质局部角度域高斯束叠前深度偏移成像[J]. 地球物理学报, 56(12): 4206-4214, doi: 10.6038/cjg20131223. |
| [92] | 段新意, 李振春, 黄建平,等. 2014. 各向异性介质共炮域高斯束叠前深度偏移[J]. 石油物探, 53(5): 579-586. |
| [93] | 黄建平, 李振春, 孔雪,等. 2013a. 碳酸盐岩裂缝型储层最小二乘偏移成像方法研究[J]. 地球物理学报, 56(5): 1716-1725, doi: 10.6038/cjg20130529. |
| [94] | 黄建平, 李振春, 刘玉金,等. 2013b. 复杂介质最小二乘叠前深度偏移成像方法研究[J]. 地球物理学进展, 28(6): 2977-2983, doi: 10.6038/pg20130619. |
| [95] | 黄建平, 曹晓莉, 李振春,等. 2014a. 最小二乘逆时偏移在近地表高精度成像中的应用[J]. 石油地球物理勘探, 49(1): 107-112. |
| [96] | 黄建平, 张晴, 张凯,等. 2014b. 格林函数的高斯束逆时偏移[J]. 石油地球物理勘探, 49(1): 101-106. |
| [97] | 黄建平, 袁茂林, 李振春,等. 2015. 双复杂条件下弹性波非倾斜叠加精确束偏移方法研究[J]. 石油物探, 54(1): 56-63. |
| [98] | 李博, 刘国峰, 刘洪. 2009. 地震叠前时间偏移的一种图形处理器提速实现方法[J]. 地球物理学报, 52(1): 245-252. |
| [99] | 李振春, 姚云霞, 马在田,等. 2003. 共反射面道集偏移速度建模[J]. 地震学报, 25(4): 406-414. |
| [100] | 李振春. 2011. 地震叠前成像理论与方法[M]. 东营: 中国石油大学出版社. |
| [101] | 林依华, 张中杰, 尹成,等. 2003. 复杂地形条件下静校正的综合寻优[J]. 地球物理学报, 46(1): 101-106. |
| [102] | 刘红伟, 李博, 刘洪,等. 2010. 地震叠前逆时偏移高阶有限差分算法及GPU实现[J]. 地球物理学报, 53(7): 1725-1733, doi: 10.3969/j.issn.0001-5733.2010.07.024. |
| [103] | 刘红伟, 刘洪, 李博,等. 2011. 起伏地表叠前逆时偏移理论及GPU加速技术[J]. 地球物理学报, 54(7): 1883-1892, doi: 10.3969/j.issn.0001-5733.2011.07.022. |
| [104] | 罗银河, 刘江平, 俞国柱. 2004. 叠前深度偏移述评[J]. 物探与化探, 28(6): 540-545. |
| [105] | 马淑芳, 李振春. 2007. 波动方程叠前深度偏移方法综述[J]. 勘探地球物理进展, 30(3): 153-161. |
| [106] | 王志亮, 周滨, 高祁,等. 2011. 高斯射线束偏移技术在渤海LD16-17区的应用[J]. 中国海上油气, 23(5): 307-308. |
| [107] | 谢飞, 李佩, 黄中玉,等. 2013. 高斯射线束叠前深度偏移成像研究[J]. 石油物探, 52(1): 65-71. |
| [108] | 徐少波, 岳玉波, 王仕俭. 2014. 弹性波高斯束叠前深度偏移[J]. 石油地球物理勘探, 49(2): 259-265, 287. |
| [109] | 岳玉波. 2011. 复杂介质高斯束偏移成像方法研究[D]. 青岛: 中国石油大学(华东). |
| [110] | 岳玉波, 李振春, 钱忠平,等. 2012. 复杂地表条件下保幅高斯束偏移[J]. 地球物理学报, 55(4): 1376-1383, doi: 10.6038/j.issn.0001-5733.2012.04.033. |
| [111] | 张春燕, 李振春, 孙小东. 2010. 逆时偏移方法技术进展综述[J]. 勘探地球物理进展, 33(5): 309-317. |
| [112] | 张丽艳, 刘洋. 2005. 转换波叠前时间偏移方法综述[J]. 地球物理学进展, 20(4): 1134-1139. |
| [113] | 张钋, 李幼铭, 刘洪. 2000. 几类叠前深度偏移方法的研究现状[J]. 地球物理学进展, 15(2): 30-39. |
| [114] | 张平平, 常旭. 2006. 保幅偏移中的权函数[J]. 地球物理学进展, 21(1): 203-207. |
| [115] | 赵连功, 刘洪. 2003. 地震勘探数据资料处理软件集成化研究现状和发展趋势[J]. 地球物理学进展, 18(4): 598-601. |
 2015, Vol. 30
2015, Vol. 30


