2. 中国国土资源航空物探遥感中心, 北京 100083;
3. 中国地质调查局, 北京 100037;
4. 河北地质职工大学, 石家庄 050081
2. China Aero Geophysical Survey & Remote Sensing Center for land and Resources, Beijing 100083, China;
3. China Geological Survey, Beijing 100083, China;
4. Hebei Vocational College of Geology, Shijiazhuang 050081, China
在国家高技术研究发展计划(863计划)“航空地球物理勘查技术系统”重大项目资助下,中国国土资源航空物探遥感中心(简称航遥中心)成功研制出具有完全自主知识产权的航磁全轴梯度勘查系统,使我国具备了开展第二阶段航磁测量(地球磁场的总磁场强度模量的空间变化率或梯度测量)飞行工作的能力(张昌达,2006).
但是航磁梯度测量并不是因为航磁全轴梯度勘查系统的成功研发才开始的,早在20世纪后期,国内相关单位引进了国外的航磁梯度勘查系统开展了航磁梯度测量工作(管志宁,1997),但其效果的好坏受到国外技术的制约现象较普遍,20世纪90年代航遥中心研发了航磁水平梯度测量系统,并在湖南的宁乡开展了试验飞行,但当时相关技术还需要进一步的改善,同时在后期梯度数据开展数据处理和地质解释时,主要以梯度数据与总场数据进行对比分析为主:王隽人和孙连池(1990)利用引进加拿大的航磁垂直梯度系统数据在冀东地区地质填图中进行了应用,指出航磁垂直梯度测量是地质填土和矿产勘探的有效手段(王隽人和孙连池,1990);管志宁等人(1996)利用引进加拿大的垂直梯度系统数据,在金矿地质填图和成矿预测中进行了应用,总结了金矿床上航磁梯度异常的变化规律,取得了较好的地质效果(管志宁等,1996);以上两篇文献都仅应用了垂向梯度进行解释,缺少了水平梯度数据.骆燕等人(2007)利用引进加拿大的垂直、水平梯度系统数据在潮水地区进行了应用,特别指出实测的垂向梯度比计算的垂向一阶导数提供的信息更丰富(骆燕等,2007);李晓禄和常树帅(2009)利用引进加拿大的垂直、水平梯度系统数据,在砂岩型铀矿勘查进行了应用,认为航磁梯度数据可以识别微弱地磁变化,但直接应用于砂岩型铀矿尚处于探索阶段,需进一步研究、验证(李晓禄和常树帅,2009);线纪安等人(2013)详细地阐述了实测航磁ΔT三维梯度与由ΔT数据换算的三维梯度数据的异同,认为在需要用航磁ΔT三维梯度数据时,只需实测航磁ΔT的横向水平梯度,其余2个方向梯度值可用由ΔT 值换算得出,即可达到解释要求(线纪安等,2013);管志宁等在磁异常梯度解释理论与方法中针对实测的航磁垂向梯度数据进行了理论分析和公式的推导,认为梯度数据在进行地质解释时有很多优势(陈国新等,1993).以上的文章都是针对实测的航磁梯度数据所开展的数据处理解释研究和应用,但是都没有涉及到梯度数据延拓转换处理方法的理论公式推导和理论模型研究,因此也就没有涉及到梯度数据进行延拓的目的和意义.
ΔT异常的求导能区分相邻磁性体的异常,减少其相互叠加的影响,或者分离叠加在背景场中的局部场;还能减轻磁性围岩的干扰,因为磁性围岩异常经过导数换算后,异常的幅度和范围都会大大减小;还能消除正常场背景值(常数)的影响,因为正常背景值的导数为零,因此对磁异常换算成导数异常后正常背景值就消失(管志宁,2005); ΔT进行向上延拓处理的主要作用是削弱局部干扰异常,突出深部较大地质体的异常,压抑浅部较小地质体的异常(焦新华和吴燕冈,2009),这些结论都是在相关文献资料中查到的,也是经得起检验的.目前我国已具备采集实测的梯度数据的能力,但是梯度数据相比于总场来说,其衰减速度相比于总场来说较快,梯度数据是否能够进行延拓处理,截至目前未见有相关文献资料对其进行阐述,或者说梯度数据能够向ΔT异常那样进行延拓转换处理,但其进行延拓转换处理的目的和意义又是什么还是没有一个比较清晰地认识.总场向上延拓的意义是突出深部异常,压制浅部异常,但是梯度数据本身就可认为是增强了浅部异常体的信号,如果梯度数据能够进行向上延拓处理,那梯度数据的延拓结果又能得出什么结论还需要进一步的研究.
因此本文首次针对实测梯度数据的延拓转换处理方法开展研究,利用理论公式推导出实测梯度数据能够进行延拓转换处理;利用简单理论模型的剖面进行理论验证,并利用复杂理论模型体群建立了梯度数据向上延拓的目的意义就是在梯度数据反映浅部异常体的基础上,能够更明显地突出埋藏相对较浅的异常,压制埋藏深度相对较深的异常;最后利用已采集的200 m和400 m飞行高度的航磁垂向梯度数据进行实际应用,并将200 m飞行高度梯度数据上延到400 m 后,开展实测的400 m飞行高度实测梯度数据的对比分析,进一步验证了梯度数据能够进行上延及其上延的目的意义及应用前景. 1 梯度数据延拓理论公式推导
梯度数据能否进行向上延拓处理,并未找到相关资料对其进行阐述(陈国新等,1993;管志宁等,1996;管志宁,1997),因此就更没有理论公式的推导来证明梯度数据能够进行延拓转换处理,本文从频率域总强度磁异常的波谱特征理论计算公式的深度因子着手,经过理论公式推导后证明总强度磁异常的深度因子与梯度异常的深度因子是一致的.
总强度磁异常的波谱特征理论计算公式已有学者进行理论推导,主要分为点极磁场的波谱理论计算公式(式1)、磁偶极异常的波谱理论计算公式(式2)、直立矩形棱柱体磁异常的波谱理论计算公式(式3)(李庆宣等,1995;胡祥云等,2012;张恒磊等,2014):
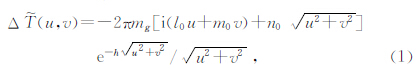
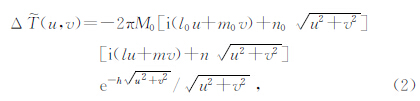
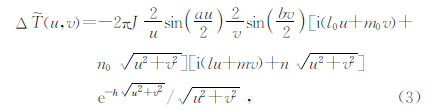
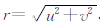 ,h为埋藏深度,l、m、n为磁化方向的方向余弦,mg为磁荷量,M0为磁偶极矩.
,h为埋藏深度,l、m、n为磁化方向的方向余弦,mg为磁荷量,M0为磁偶极矩.
在进行解析延拓时,计算平面的场与实测平面的场的区别,只是在于他们离场源的距离不用,由磁异常波数谱特点可知,这两个平面上的异常波数谱仅在于其深度因子有所区别,因此,从式1~3可以看出,磁异常的延拓异常波数谱只和深度因子和圆频率有关,因此可以得出如下的简单公式为

以上公式的建立为推导实测的梯度数据是否能够进行向上延拓处理奠定了基础性的理论计算前提,本文的主要目的是证明是实测的梯度数据也能够进行向上延拓,这样才能够继续开展实测梯度数据在进行延拓时针对各种规律的解释分析,那么在证明梯度数据也能够进行延拓转换处理的思路主要有如下三个方面:
(1)首先开展梯度数据的延拓处理,这样就可以得出延拓后梯度数据的波谱理论计算公式的特征.
(2)开展总强度磁异常波谱的延拓计算公式的x、y、z方向的求导的理论计算公式的推导,得出其理论计算公式的特征.
(3)分析由(1)和(2)推导出的理论计算公式,如果一致说明梯度数据的延拓处理与总强度磁异常进行延拓后求导的处理结果一致,那么梯度数据可以直接进行延拓处理. 1.1 垂向梯度数据能够进行延拓的理论计算公式推导证明 1.1.1 实测垂向梯度数据波谱的延拓理论公式推导
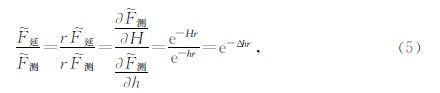

推导
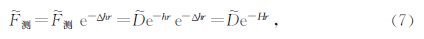
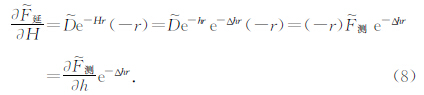
由理论计算推导出的式6和式8可以看出,实测的垂向梯度数据经过延拓后的波谱理论计算公式与实测的ΔT延拓后再求垂向导数的理论计算公式是一致的,说明实测的垂向梯度数据在理论上是可以进行延拓的数据处理计算. 1.2 x方向梯度数据能够进行延拓的理论计算公式推导证明 1.2.1 实测x方向梯度数据波谱的延拓理论公式推导
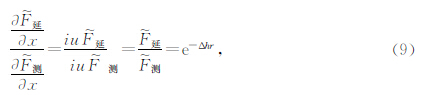
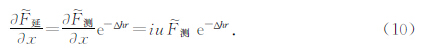
推导

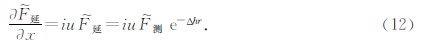
同样的由理论计算推导出的式10和式12可以看出,实测的x方向梯度数据(横向梯度数据)波谱经过延拓后的波谱理论计算公式与实测的ΔT延拓后再求x方向导数的理论计算公式是一致的,说明实测的x方向梯度数据在理论上是可以进行延拓的数据处理计算.同理,y方向梯度数据(纵向梯度数据)波谱在理论上也是可以进行延拓的数据处理计算.
由此可得出结论,式4也同样适用于实测的梯度数据,但是梯度数据的向上延拓的目的和意义还需要进一步的研究,也需要为后期梯度数据的解释工作奠定基础,而这些内容也同样未见有相关资料阐述. 2 模型试验
经理论计算公式推导证明,实测的横向梯度、纵向梯度和垂向梯度数据是可以进行延拓转换处理的,但是梯度数据的延拓转换处理结果是否能够达到总强度磁异常延拓处理后的目的意义还需要进一步的分析研究,同时梯度数据的延拓结果与总场数据延拓后的梯度数据解释结果是否一致也需要进一步的分析研究,如果能够寻找出其梯度数据进行延拓后的在地质体解释上的规律性,将为为今后开展梯度数据的延拓转换处理解释奠定扎实的基础.
为了能够较好的进行分析解释,首先设置了单一模型体及多个模型体来进行地质解释前的分析研究,以便寻找出梯度数据延拓处理的解释思路. 2.1 单一模型体上延一定高度后的异常曲线特征研究
设置单一简单模型体的目的就是为了能够对实测梯度数据上延及转换的梯度数据上延后的数据结果进行一次清晰地量化分析.
在该简单理论模型体中,设置其为400 m×400 m×400 m的立方体,顶面埋深为300 m,其磁化强度为20 A/m,同时将该模型体设置为垂直磁化,图 1为该模型体的XY平面位置图,由该简单模型体所得到的横向梯度等值线图,在沿X=2000 m方向的二维异常特征为波峰和波谷交替出现的结果,共出现两个波峰和波谷,在Y=2000 m方向是一个梯度正值波峰;由该简单模型体所得到的纵向梯度等值线图,在沿Y=2000 m方向的二维异常特征为波峰和波谷交替出现的结果,共出现两个波峰和波谷,在X=2000 m方向是一个梯度正值波峰,可见横向梯度与纵向梯度之间的等值线形态发生了90°旋转;由该简单模型体所得到的垂向梯度等值线图是以中心点呈中心对称的分布形态,其在沿X=2000 m或Y=2000 m方向的二维异常特征都是一致的,即都有一个波峰和两个波谷,且两个波谷都为负值;因此图中的直线说明将梯度数据从Y=2000 m的位置处抽取一条剖面,随后针对实测梯度数据及转换梯度数据的延拓转换处理曲线进行对比分析研究,图 2 为该模型体的XZ平面位置图;
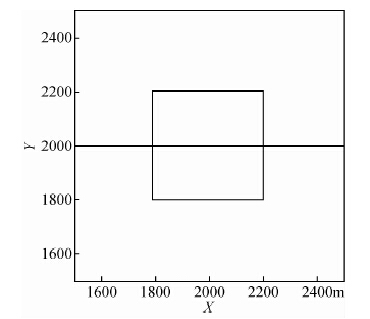 | 图 1 模型体XY平面位置图 Fig. 1 XY plane profile of the theoretical model |
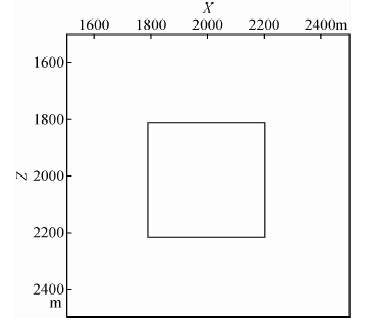 | 图 2 模型体XZ平面位置图模型体为立方体,边长400 m,顶面埋藏深度300 m,垂直磁化,磁化强度20 A/m. Fig. 2 XZ plane profile of the theoretical model The model body is a cube,with length of 400 m,buried depth of 300 m,and vertical magnetization,with magnetization intensity of 20 A/m. |
虽然理论计算公式推导的结果说明,实测的梯度数据进行上延处理和实测的ΔT数据进行求导后上延的结果是一致的,但是还需要有理论模型对应的曲线特征进行对比分析,为了达到这个目的,本文同样将实测的ΔT数据进行求导后上延200 m的位场处理,同样抽取Y=2000 m所对应的横向梯度、纵向梯度和垂向梯度数据剖面曲线,见图 3、图 4和图 5中的红色曲线.从图 4和图 5中可以看出实测梯度数据的延拓曲线和ΔT数据求导后上延曲线对应的较好,再一次说明梯度数据是完全可以进行延拓转换处理的,从图 3中可以看出,实测梯度数据的延拓曲线和ΔT数据求导后上延曲线对应的有所差异,是因为横向梯度上延200 m,在Y=2000 m所对应的那条剖面曲线的梯度异常值较小,在进行剖面曲线绘制时,y轴的比例尺相比于图 4和图 5有所放大的缘故,其异常形态是一致的.
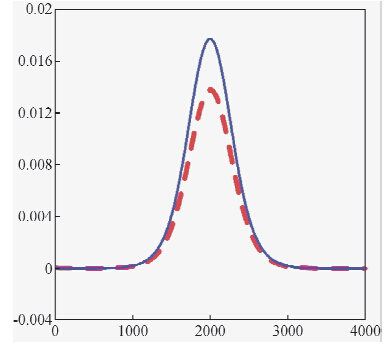 | 图 3 横向梯度剖面图 Fig. 3 Traverse gradient profile map |
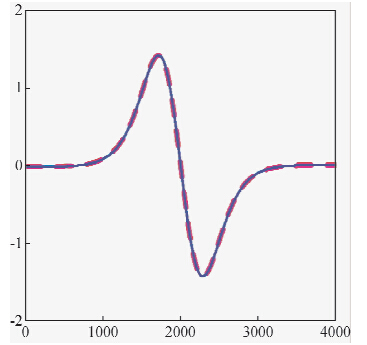 | 图 4 纵向梯度的剖面图 Fig. 4 Longitudinal gradient profile map |
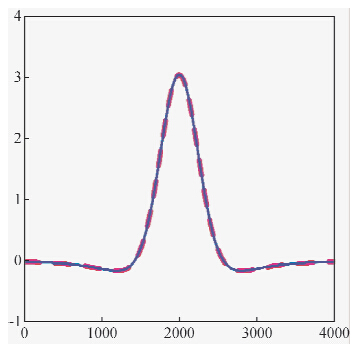 | 图 5 垂向梯度的剖面图蓝线是实测梯度数据上延200 m;红线是总场转换梯度数据上延200 m. Fig. 5 Vertical gradient profile map |
在对复杂模型体群进行研究前,由于横向梯度数据是沿着X方向异常反映,纵向梯度数据是沿着Y方向的异常反映,在模型体上的异常反映特征都是正负相间的,该两种梯度数据异常形态为呈90°旋转对应状态,且梯度值在模型体上是一致的,因此讨论横向梯度数据就不再讨论纵向梯度数据,因为横向梯度数据的异常特征适用于纵向梯度数据的异常特征;同时横向梯度与垂向梯度延拓的目的、意义及异常形态规律特征也是一致的,因此本文将着重研究复杂模型体群利用垂向梯度数据进行上延前后得到的等值线规律特征.
在该复杂模型体群中,首先设置了一个背景场,为1500 m×1500 m×1500 m的立方体,顶面埋深为1000 m,其磁化强度为10 A/m,称为模型体1;在该磁性体正上方设置一个400 m×400 m×400 m的立方体,顶面埋深为200 m,其磁化强度为10 A/m,称为模型体2;在坐标为(2861,1567)位置处设置了一个400 m×400 m×400 m的立方体,顶面埋深为500 m,其磁化强度为20 A/m,称为模型体3;在坐标为(1265,2874)位置处设置了一个200 m×200 m×200 m的立方体,顶面埋深为100 m,其磁化强度为20 A/m,同时将该四个模型体群都设置为垂直磁化称为模型体4.图 6为该模型体群的XY平面的位置图,图 7为该模型体群的XZ平面的位置图,图 8和图 9分别为垂向梯度平面等值线图和垂向梯度上延250 m的平面等值线图,从图 8可以看出,模块体2和模块体4较清晰地反映出了地质体的边界位置,且边界位置处的梯度异常很大,模块体3也反映出了地质体的边界,但是并不是很清晰,从图 9可以看出,通过上延250 m后,模块体3的形态已基本无法识别,但是模块体4的形态反映依然比较强烈,模块2的边界也依然清晰可见,同样也说明,梯度数据对于单独的模块体反映较明显,相比于总场来说,其区分模块体的能力更强、更大,另外从图 9中可以看出,垂向梯度数据的负异常正在向北西方向移动,这也符合异常反映的规律,由此获得结论一:
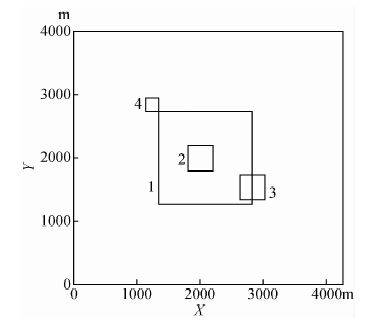 | 图 6 模型体XY平面位置图XY Fig. 6 plane profile of the theoretical model |
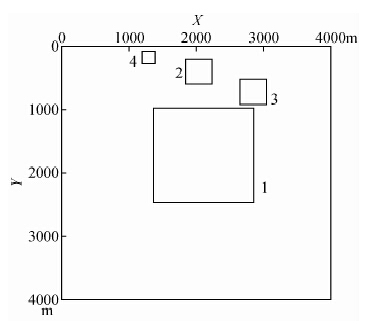 | 图 7 模型体XZ平面位置图 Fig. 7 XZ plane profile of the theoretical model |
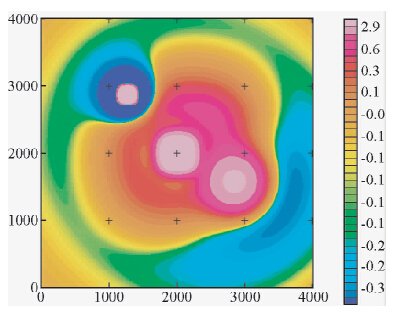 | 图 8 垂向梯度平面等值线图 Fig. 8 Contours plane graph of vertical gradient |
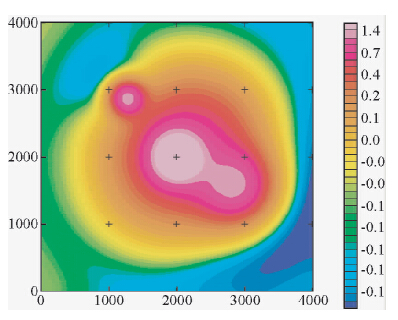 | 图 9 垂向梯度上延250 m平面等值线图 Fig. 9 Contours plane graph of vertical gradient with upward extending 250 m |
针对梯度数据来说,模块体3和模块体4相比,虽然具有同样的磁化强度,且模块体3的体积是模块体4的8倍,但是由于模块体3的埋深相比于模块体4的埋深更大,通过上延处理后导致模块体3的衰减速度更快,由此初步认为梯度数据上延后突出了相对埋深较浅的异常体,该结论的正确性将在2.3部分做深入研究.
为了对比实测的梯度数据和由ΔT异常转换得到的梯度数据的效果,也针对ΔT异常转换得到的垂向梯度和横向梯度数据上延250 m,得到图 10显示的结果,从图 10中可以看到ΔT数据经过垂向梯度处理后又经过上延数据处理,其正值异常的形态并没有变化,但是负值的异常形态却变化较大,通过对比图 9和图 10得知西北方向和东南方向的负值区域已经完全不是同一个形态,为了呈现实测梯度数据及转换处理得到的梯度数据上延250 m后得到的数据结果的误差,特开展了垂向梯度数据上延前后数据之间的差,结果见图 11,可见这两个图中的值都不是很大,在图 11中可以看到数据在-0.15~-0.09之间,图 11的误差呈现出沿着垂直方向的变化;由此获得结论二:
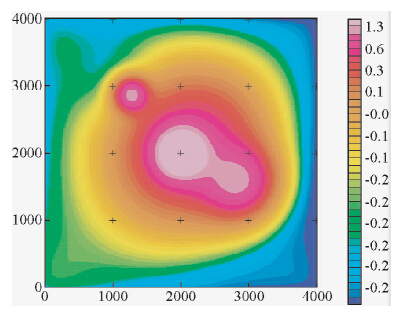 | 图 10 ΔT转换的垂直梯度上延250 m平面等值线图 Fig. 10 Contours plane graph of vertical gradient with upward extending 250 m after ΔT transform |
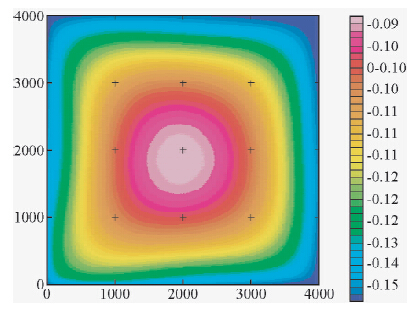 | 图 11 图 10与图 9差的平面等值线图 Fig. 11 Contours plane graph of different between fig.10 and fig.9 |
在获得ΔT异常后进行数据处理时,往往需要经过各种转换处理方法,实测的梯度数据一直保持着原始性,而转换的梯度数据已经经过各种转换处理办法后失去了一些有效的信息,因此开展实测梯度数据延拓处理的可行性就完全有这个必要. 2.3 梯度数据上延不同高度的规律性研究
复杂模型体群引起的梯度异常数据上延到一个高度的异常曲线特征已经进行了讨论,如果将梯度异常数据上延到不同高度后异常曲线特征还需要进一步的讨论.
在图 9中已经给出了垂向梯度数据上延250 m后的平面等值线图,这个延拓高度并没有超过模块体4的底界面的埋藏深度300 m,在该异常图中,模块体2和模块体4的梯度异常反映相对来说还是较强烈的,但是模块体3的梯度异常反映就弱很多,从图 12中可以看出,垂向梯度已经上延了400 m,已经超过了模块体4的底界面埋深,但是模块体4所引起的梯度异常依然清晰可见,模块体2和模块体1的异常基本上已经融为一体,无法判断是否是模块体2所引起的梯度异常,模块体3的梯度异常还能显现出来,从图 13中可以看出,垂向梯度数据已经上延了600 m,与模块体2的底界面埋深相同,超过了模块体3的顶界面埋深,但是模块体4的梯度异常反映还存在,模块体3的梯度异常对模块体1和模块体2的影响还能看到,当上延到900 m高度时见图 14,基本上就只有背景场的梯度异常了,通过分析可以得出结论三:对于梯度异常而言,浅部的地质体所引起的梯度异常随着上延高度的增加即使高度高于该地质体底界面埋深,但是梯度异常反映依然有可能存在,深部异常体所引起的梯度异常随着上延高度的增加即使还没有延拓到该地质体顶界面埋深,梯度异常反映可能已经非常微弱了.
 | 图 12 垂向梯度上延400 m平面等值线图 Fig. 12 Contours plane graph of vertical gradient with upward extending 400 m |
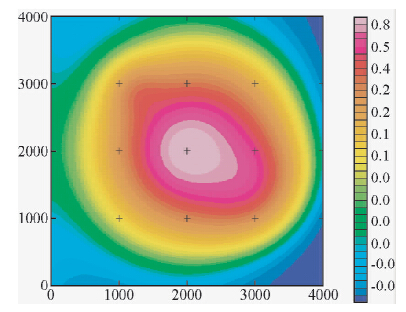 | 图 13 垂向梯度上延600 m平面等值线图 Fig. 13 Contours plane graph of vertical gradient gradient with upward extending 600 m |
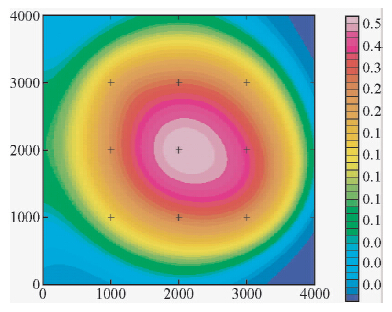 | 图 14 垂向梯度上延900 m平面等值线图 Fig. 14 Contours plane graph of vertical gradient with upward extending 900 m |
综上所述:单一理论模型显示的结果表明梯度数据可以进行延拓转换理论进行数据处理,这也和理论计算公式推导出的结果一致并相互佐证;复杂理论模型体群的梯度数据的上延转换处理后得出:当模型体具有同样磁化强度的情况下,深部地质体的梯度异常上延后的梯度数据衰减快于浅部的地质体;利用实测的梯度数据进行延拓后的结果相比于ΔT异常求导后再上延的结果更接近于真实的情况;梯度数据的上延处理突出了浅部的异常体,与相对于埋藏较深的异常体进行了压制,但这是在梯度数据相对于总场而言突出浅部异常体的前提下成立的,这为在梯度解释中分离深部异常体和浅部异常体提供了有效证明.所有这些结论的获得,既极大地丰富了梯度数据的解释技术,也为梯度数据经上延转换处理后较好地分离深部异常体和浅部异常体提供了有效的方法技术手段. 3 实测获得的梯度数据
实测的梯度数据主要有横向梯度、纵向梯度和垂向梯度三个参量数据,2012年以前出现的梯度测量模式主要有水平梯度测量(横向梯度、纵向梯度)或垂向梯度测量,且存在国外引进的垂向梯度或水平梯度测量仪器,但并未见有水平梯度和垂向梯度同时测量的方式出现,这也主要是由于各探头数据收录的高度同时性和梯度数据补偿效果还没有得到较好解决的原因等的影响,2012年航遥中心通过各方面的努力,克服了各种技术瓶颈,各项硬件和软件技术都实现了国产化,开展了总场、水平梯度和垂向梯度同时测量的模式,这种模式也称之为航磁全轴梯度测量,这种测量模式获得的数据有横向梯度、纵向梯度、垂向梯度和总场四个参量数据,也同时代表了我国具备了开展第二阶段航磁测量(地球磁场的总磁场强度模量的空间变化率或梯度测量)飞行工作的能力(张昌达,2006).
实现航磁全轴梯度的测量,需要拥有四个磁探头,其安置结构见图 15,飞机两个翼各安装一个探头、尾部竖直安装两个探头.左、右,后上、后下四个探头分别可测得 TL、TR、TU、TD四个地磁场总强度,通过四道磁力仪间地磁场总强度的差值近似计算梯度(式13~15):

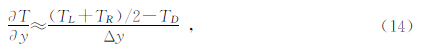

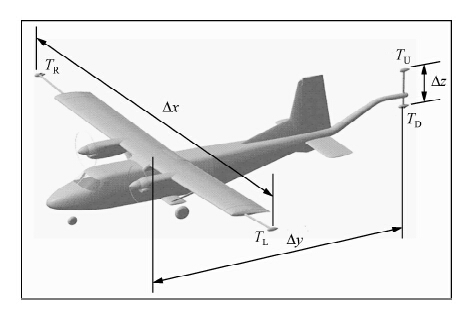 | 图 15 航磁全轴梯度测量装置示意图 Fig. 15 map of tri-axial aeromagnetic gradient measurement system |
为了开展梯度数据的应用解释工作,在中国北部某地开展了航磁全轴梯度测量工作,该测区属农田区,西部相对偏高,海拔50~408 m,中东部较低,海拔17~50 m,地形起伏较平缓,鉴于该测区的地质走向及科研工作需要,飞行高度设置为200 m和400 m两个不同高度,测量飞行的测线方向为正南北向,测区测量比例尺为12.5万,为了后期梯度数据的调平工作,在东西向同时开展了切割线飞行工作,切割线间距为1000 m,同时为了消除实测总场中日变因素的影响,在测区内同样开展了磁日变的观测工作,这样就最终分别获得了200 m和400 m飞行高度的横向梯度、纵向梯度、垂向梯度和总场数据.
所获得两个不同高度的梯度数据,也为研究梯度数据经过上延后的梯度等值线图与实际飞行高度的梯度等值线图进行对比,进而讨论梯度数据的实际应用效果如何,提供了基础性的实际应用资料. 4 实际数据的应用分析
通过理论计算公式推导和理论模型证明,梯度数据完全可以进行延拓转换处理,且在梯度数据相比于总场突出浅部异常体的情况下,能够突出埋深相对较浅的异常体,压制埋深相对较深的异常体,但是理论模型的设置毕竟是理想状态下的,它只能对梯度数据上延后的异常显示规律进行分析解释,为实际应用提供理论基础,然而实测的梯度数据反映的是非常复杂的地质体环境,对于真正实测的梯度数据上延效果是否能够达到突出浅部异常体还需要进一步的分析,尤其当浅部异常体位于埋藏相对较深异常体正上方时,浅部梯度异常同样会被叠加到较深部异常体中,如果利用梯度数据进行延拓处理后突出浅部异常,将会对地质解释效果起到重要的作用.
由于本次在中国北部地区开展的航磁全轴梯度测量进行了两个不同的飞行高度的梯度飞行试验,一个是200 m高度的航磁全轴梯度数据,另一个就是400 m高度的航磁全轴梯度数据,现仅提取出垂向梯度数据进行上延效果的对比分析,见图 16为飞行高度200 m的垂向梯度平面等值线图,通过对200 m高度的垂向梯度数据进行上延200 m的数据转换处理获得平面等值线图见图 17,将该图的效果与400 m飞行高度实测的垂向梯度数据形成平面等值线图见图 18进行对比,首先通过计算得出:200 m飞行高度的垂向梯度数据上延200 m后的数据最大值为1591 nT/km,最小值为-787 nT/km;400 m高度实测的垂向梯度数据最大值为1595 nT/km,最小值为-899 nT/km,数据结果显示图 17和图 18梯度异常形态和规模都是比较接近的,因此梯度数据是能够进行延拓转换处理方法开展研究.
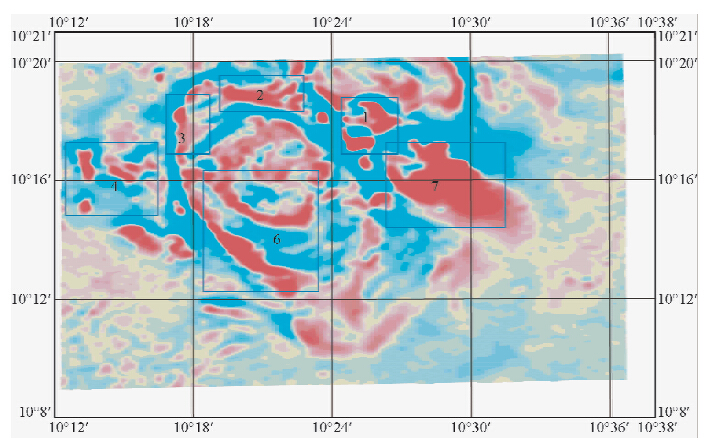 | 图 16 200 m飞行高度的垂向梯度数据 Fig. 16 Vertical gradient data from 200 m flight height |
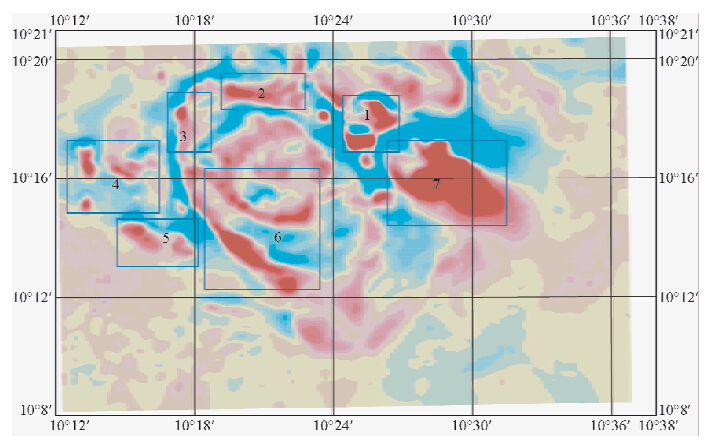 | 图 17 200 m飞行高度的垂向梯度数据上延200 m Fig. 17 Upward extending 200 m of vertical gradient data from 400 m flight height |
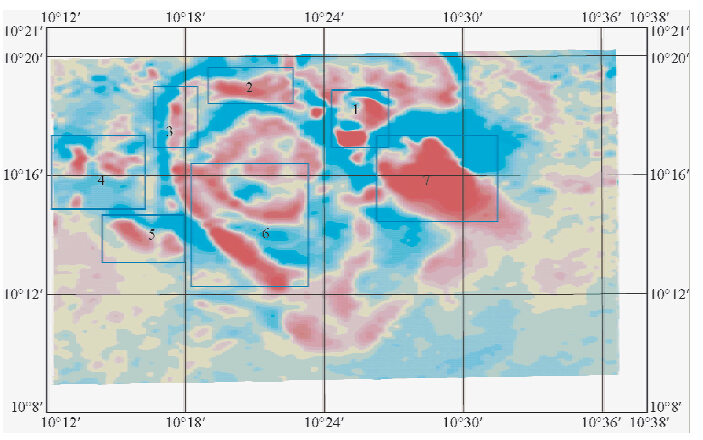 | 图 18 400 m飞行高度的垂向梯度数据 Fig. 18 Vertical gradient data from 400 m flight height |
为了对该测区的地质成矿规律进行深入了解,根据所收集的地质资料将200 m飞行高度的垂向梯度数据平面图(见图 16)中显示的异常区域划分为7个异常区,必须说明的是占该测区面积四分之三的中东部基本上全部由第四系覆盖,但该区域在20世纪50年代开展地质调查工作时在多处区域打过钻,这也为证明梯度数据的向上延拓的效果提供了较好的地质资料,第1个异常区内南部异常经过打钻验证为含铁角闪岩,其中铁含量达到20%左右,该钻为50年代所打,最大深度为400 m左右;第2个异常区内的异常,推断与磁铁矿有关;第3个异常区内的异常,经50年代打钻证实,为隐伏的铁铜矿,同样该钻最大深度为400 m左右;第4个异常区内的异常为矽卡岩型金属矿所引起,该处正在进行矿产的开采工作,异常体顶部埋藏深度并不大;第5个异常区具有良好的成矿条件,为接触交代蚀变岩引起;第6个异常区下部北西向异常带见有接触交代型铁矿,同样埋藏深度并不 大;第7个异常区主要为有一定规模的基性岩体引起,经50年代打钻证实主要含磁铁角闪岩,该钻最大深度为400 m左右.
从图 16可以看到相对较深的梯度异常和浅部的梯度异常叠加在一起,并不容易分辨出来,同时根据已知的地质资料所圈定的7个异常区中的异常反映效果并不比7个异常区外的异常反映更强烈,图 17是该区域实测的垂向梯度上 延200 m后的平面等值线图,图 18为该区域飞行高度400 m 的实测垂向梯度平面等值线图.从图 17中可以看出,经过上延200 m后的梯度异常相比于实测的梯度异常已经有了突出的作用,而且所突出的异常都位于在图 16基础上绘制的7个异常区内,且该7个异常区内的异常埋藏深度并不深,由此可以证明上延后的梯度数据所突出的梯度异常说明该处的地质体埋藏深度相比来说会比较浅;从图 18中可以看出,相比于图 16飞行高度为200 m的实测垂向梯度数据来说,400 m飞行高度获得的垂向梯度数据所绘制的平面图反映的异常大小有了层次感,其层次感与图 17的层次感非常相似,即反映比较强烈的异常主要分布在7个异常区内,且这些异常埋藏的深度并不大,这也从侧面利用实测的梯度数据进一步的证实了梯度数据进行延拓后的目的意义与理论模型得出的结论是一致的,但是从图 18中看出,相比于图 17而言,异常的层次感反映并没有图 17反映的强烈,这主要是由于梯度数据经过向上延拓处理后,使得高频信号得到增强的原因.
由此应用实例可以得出:一是经过上延后的梯度数据对于浅部异常的突出效果非常明显,尤其在第四系覆盖较严重的区域,上延后的梯度数据能够提供更明显的异常信息,给地球物理解释工作带来了极大的便利;二是通过200 m和400 m两个不同飞行高度的梯度数据可以看出,200 m飞行高度的梯度数据经过向上延拓处理后的效果与400 m飞行高度的梯度数据显示的结果基本一致. 5 结 论 5.1 本文通过理论公式的推导说明实测的梯度数据是可以进行延拓转换处理的,并利用所设置了单一理论模型体进行了辅助证明;为了研究梯度数据向上延拓的理论意义,设置了复杂模型体群开展了理论研究,得出了以下结论:当模型体具有同样磁化强度的情况下,埋藏相对较深的地质体梯度异常上延后的梯度数据衰减快于浅部的地质体;利用理论上实际产生的梯度数据进行延拓后的结果相比于ΔT异常求导后再上延的结果更接近于真实的情况;梯度数据的上延处理突出了浅部的异常体,对相对较深的异常体进行了压制,这样的结论也完全是在梯度数据突出浅部异常的理论前提下才成立.
5.2 这些理论意义的适用性同时得到了航遥中心开展的200 m和400 m飞行高度的航磁全轴梯度测量,所采集到的不同高度的梯度数据的验证,以垂向梯度数据为例,将实测的200 m飞行高度的垂向梯度数据上延200 m后对比实测的400 m飞行高度的垂向梯度数据认为,利用梯度数据上延处理突出了浅部异常体,压制了相对较深的异常体,这样可以有效地分离出实测梯度数据中所叠加的相对较深的地质体产生的梯度异常,为今后大规模地开展航磁梯度测量工作奠定了较好的解释理论基础.| [1] | Chen G X, Guan Z N, Yao C L, et al. 1993. The explanation theory and method of Magnetic anomaly gradient (in Chinese)[R]. The national natural science fund achievement report. |
| [2] | Di Q Y, Fang G Y, Zhang Y M. 2013. Research of the surface electromagnetic prospecting (SEP) system[J]. Chinese Journal of Geophysics (in Chinese), 56(11): 3629-3639, doi: 10.6038/cjg20131104. |
| [3] | Guan Z N, Hou J S, Yao C L. 1996. Application of aeromagnetic gradient data in geological mapping and metallogenetic prognosis of gold deposits[J]. Geosciences (in Chinese), 10(2): 239-249. |
| [4] | Guan Z N. 1997. Researches and progresses of magnetic prospecting in China[J]. Acta Geophysica Sinica (in Chinese), 40(S1): 299-307. |
| [5] | Guan Z N. 2005. Geomagnetic Field and Magnetic Exploration (in Chinese)[M]. Beijing: Geological Publishing House, 175. |
| [6] | Jiao X H, Wu Y G. 2009. Gravity and Magnetic Exploration (in Chinese)[M]. Beijing: Geological Publishing House, 196-199. |
| [7] | Li Q X, Sun Y S, Xu H P, et al. 1993. Image Processing and Programming of Geophysical Potential Field Data Transformation (in Chinese)[M]. Changchun: Jilin Science & Technology Press, 10-78. |
| [8] | Li X L, Chang S S. 2009. Aeromagnetic gradient survey and elementary application in sandstone type uranium deposits prospecting[J]. Uranium Geology (in Chinese), 25(6): 355-360. |
| [9] | Luo Y, Li X L, Cai W L, et al. 2007. Preliminary analysis of aeromagnetic gradient experimental flight data in Chaoshui basin[J]. Journal of East China Institute of Technology (in Chinese), 30(2): 164-170. |
| [10] | Wang J R, Sun L C. 1990. The effectiveness of aeromagnetic vertical gradient survey in geological mapping of eastern Hebei. Geophysical and Geochemical Exploration (in Chinese), 14(6): 472-476. |
| [11] | Xian J A, Guo Y F, Liang J, et al. 2013. Difference of the measured 3-dimension ΔT gradient of air magnetic survey and conversion of the 3-dimension ΔT gradient[J]. Contribution to Geology and Mineral Resources Research (in Chinese), 28(2): 297-300. |
| [12] | Zhang C D. 2006. Airborne tensor magnetic gradiometry—The latest progress of airborne magnetometric technology[J]. Chinese Journal of Engineering Geophysics (in Chinese), 3(5): 354-361. |
| [13] | Zhang H L, Hu X Y, Liu T Y. 2012. Fast inversion of magnetic source boundary and top depth via second order derivative[J]. Chinese Journal Geophysics (in Chinese), 55(11): 3839-3847, doi: 10.6038/j.issn.0001-5733.2012.11.031. |
| [14] | Zhang H L, Marangoni Y R, Zuo R G, et al. 2014. The improved anisotropy normalized variance for detecting non-vertical magnetization anomalies[J]. Chinese Journal Geophysics (in Chinese), 57(8): 2724-2731, doi: 10.6038/cjg20140830. |
| [15] | 陈国新, 管志宁, 姚长利,等. 1993. 磁异常梯度解释理论与方法[R]. 国家自然科学基金成果报告. |
| [16] | 底青云, 方广有, 张一鸣. 2013. 地面电磁探测系统(SEP)研究 [J]. 地球物理学报, 56(11): 3629-3639, doi: 10.6038/cjg20131104. |
| [17] | 管志宁, 侯俊胜, 姚长利. 1996. 航磁梯度资料在金矿地质填图和成矿预测中的应用[J]. 现代地质, 10(2): 239-249. |
| [18] | 管志宁. 1997. 我国磁法勘探的研究和进展[J]. 地球物理学报, 40(S1): 299-307. |
| [19] | 管志宁. 2005. 地磁场与磁力勘探[M]. 北京: 地质出版社, 175. |
| [20] | 焦新华, 吴燕冈. 2009. 重力与磁法勘探[M]. 北京: 地质出版社, 196-199. |
| [21] | 李庆宣, 孙运生, 许惠平,等. 1995. 地球物理位场数据转换图像处理及编程[M]. 长春: 吉林科学技术出版社, 10-78. |
| [22] | 李晓禄, 常树帅. 2009. 航磁梯度测量及其在砂岩型铀矿勘查中的应用初探[J]. 铀矿地质, 25(6): 355-360. |
| [23] | 骆燕, 李晓禄, 蔡文良,等. 2007. 潮水地区航磁梯度初步分析[J]. 东华理工学院学报, 30(2): 164-170. |
| [24] | 王隽人, 孙连池. 1990. 航磁垂直梯度测量在冀东地区地质填图中的作用[J]. 物探与化探, 14(6): 472-476. |
| [25] | 线纪安, 郭玉峰, 梁建,等. 2013. 实测航磁ΔT 三维梯度与由ΔT数据换算的三维梯度数据的异同[J]. 地质找矿论丛, 28(2): 297-300. |
| [26] | 张昌达. 2006. 航空磁力梯度张量测量—航空磁测技术的最新进展[J]. 工程地球物理学报, 3(5): 354-361. |
| [27] | 张恒磊, 胡祥云, 刘天佑. 2012. 基于二阶导数的磁源边界与顶部深度快速反演[J]. 地球物理学报, 55(11): 3839-3847, doi: 10.6038/j.issn.0001-5733.2012.11.031. |
| [28] | 张恒磊, Marangoni Y R, 左仁广等. 2014. 改进的各项异性标准化方程探测斜磁化磁异常源边界[J]. 地球物理学报, 57(8): 2724-2731, doi: 10.6038/cjg20140830. |
 2015, Vol. 30
2015, Vol. 30

