地球物理学进展  2015, Vol. 30 Issue (3): 1205-1213   PDF    
引用本文
李晓峰, 黄建平, 李振春, 刘培君. 基于反稳相滤波的边缘绕射成像方法研究[J]. 地球物理学进展, 2015, 30(3): 1205-1213, doi: 10.6038/pg20150328  
LI Xiao-feng, HUANG Jian-ping, LI Zhen-chun, LIU Pei-jun. Edge diffraction imaging method based on anti-stationary phase filtering. Progress in Geophysics, 2015, 30(3): 1205-1213, doi: 10.6038/pg20150328   
基于反稳相滤波的边缘绕射成像方法研究
李晓峰, 黄建平, 李振春, 刘培君     
中国石油大学地球科学与技术学院地球物理系, 青岛 266580
收稿日期: 2014-06-06 修回日期: 2014-12-16 .
基金项目：国家重点基础研究发展计划(973)(2011CB202402, 2014CB239006),国家自然科学基金(41104069,41274124),山东省自然科学基金(ZR2011DQ016)及中央高校基本科研业务经费专项资金(R1401005A)联合资助.
作者简介：李晓峰,男,1989年生,在读硕士研究生,主要从事复杂介质成像和非均质绕射目标成像研究.(E-mail:lxfldd@126.com)
摘要：绕射波是地下小尺度不连续体的地震响应,是对地下断层、尖灭点、河道边界等高精度成像的关键.为了充分利用绕射波信息,本文通过在传统的Kirchhoff偏移算子中引入反稳相滤波器,使满足Snell定律的镜面反射得到有效压制,从而凸显绕射能量;进一步,针对边缘绕射存在的极性反转现象,在成像过程中引入校正极性算子实现边缘绕射正确成像.在实现方法的基础上,通过理论模型和实际资料边缘绕射成像试处理发现:本文方法能有效改善断点及断层边界成像质量,提高地震解释精度;通过极性校正,能一定程度提高边缘绕射点成像分辨率.
关键词： 边缘绕射波     反稳相滤波器;     极性反转;     小尺度地质不连续体    
Edge diffraction imaging method based on anti-stationary phase filtering
LI Xiao-feng, HUANG Jian-ping, LI Zhen-chun, LIU Pei-jun    
Department of Geophysics, School of Geosciences, China University of Petroleum, Qingdao 266580, China
Abstract: As the seismic response of small-size geologic discontinuities, diffraction is of great value for the high resolution imaging of faults, pinch-outs and channel edges. In order to make full use of the information carried by diffraction, this paper apply an anti-stationary phase filtering inside the traditional Kirchhoff pre-stack migration operator, which effectively attenuates events energy satisfying Snell's law. In addition, considering the polarity reversal of edge diffraction, a polarity correction operator is introduced to improve the edge diffraction image during the migration. Edge diffraction imaging both for theoretical model and field data draw the following conclusions: this method can effectively improve the image quality of breakpoints and fault boundary, leading a high resolution result for seismic interpretation; Benefit from the polarity correction, our method can also improve the imaging resolution of the edge diffraction.
Key words: edge diffraction     small-scale geological discontinuities     anti-stationary phase filtering     polarity reversal    
0 引 言

作为当前高分辨率地震勘探的主要目标，断层、裂缝、尖灭等小尺度不连续构造的地震响应主要表现为绕射波(Fomel et al.，2007；Landa et al.，2008；Berkovitch et al.，2009；Reshef and Landa，2009；Klokov et al.，2010；Zhu and Wu，2010；黄建平等，2012)，因此，绕射波成像具有高分辨率，能够准确描述断层和边界. 然而，常规地震数据处理(NMO、叠加等)以反射波为有效信号，反射波之外的同相轴往往被视为噪音而压制(Khaidukov et al.，2004； Bansal and Imhof，2005；Berkovitch et al.，2009)；地震资料中的绕射能量通常比反射能量弱一到两个数量级(Landa et al.，2008；Berkovitch et al.，2009； Klokov et al.，2010；Bai et al.，2011)，即使将其偏移归位，也不容易从全波场中识别出绕射波. 因此，如何充分利用地震数据中的绕射信息，实现绕射波单独成像，对改善绕射目标的成像分辨率，提高地震解释的精度有着重要的意义.

早在20世纪50年代，Krey(1952)和Hagedoorn(1954)已经意识到绕射波的重要性. 近年来，为了提高地震解释的精度，降低勘探开发的风险，提高采收率，各种绕射波成像方法相继提出. 根据波场分离所处的地震数据处理的不同阶段可将绕射波分离方法归纳为以下几类：

第一类，基于叠前地震数据的绕射波分离方法.该类方法依据反射和绕射波场在叠加前的不同道集上的时差、波形等特征差异，从全波场中提取绕射能量，然后再对分离出的绕射波单独成像. Landa等(1987)通过相位校正和定性分析检测共偏移距道集上的绕射体；Nowak等(2004)根据炮记录中反射波与绕射波同相轴横向位置的差别，在Radon变换域中实现波场分离；Bansal和Imhof(2005)对比了七种直接在叠前数据上增强绕射信号、压制反射波的流程，结果表明：本征矢量法是较为有效的绕射波分离方法；Taner等(2006)，孔雪等(2012)，刘玉金等(2013)以及朱生旺等(2013)通过平面波分解生成平面波记录，根据绕射波和反射波在平面波记录上的时距曲线差异，应用平面波解构滤波技术压制平滑连续的拟线性反射波，分离出绕射波.

第二类，在叠加过程中，进行绕射波分离的方法.反射叠加类：Khaidukov等(2004)在假想的源点聚焦反射波，然后从全波场中将反射聚焦点去除，对剩余波场反聚焦，得到包含大部分绕射能量的共炮点记录，最后进行绕射单独成像；绕射叠加类：不同于传统的共中心点(CMP)叠加，Kanasewich、Phadke等(1988)建议通过对地震信号沿着绕射曲线进行叠加来建立绕射时间剖面；与其他方法将反射波压制后的剩余波场作为绕射能量不同，Berkovitch等(2009)提出的绕射多聚焦叠加方法仅将绕射波同相轴最优叠加；Endrias等(2011)基于修正的共反射面(CRS)技术分别实现并讨论了相似度和多信号分类两种方法在绕射波分离中的优势.

第三类，在偏移过程中，实现绕射波分离的方法. Zhu Xiaosan和Wu Rushan(2010)在小波束偏移过程中，基于在角度域局部成像矩阵中反射能量沿着一定的倾角方向呈线性分布、绕射能量在整个矩阵中呈弥散分布的差异，识别绕射波并对其成像. 根据倾角域共成像点道集上反射波双曲、绕射波拟线性的特征，Landa等(2008)利用平面波解构滤波技术，Klokov等(2010)利用相似度扫描反射顶点去除与混合Radon变换相结合的方法在倾角域共成像点道集上进行绕射波场分离；孙赞东等(2012)在倾角域利用反射波广义拉东谱的方法实现了反射波和绕射波的分离；Bai Y等(2011)在倾角域应用中值滤波器实现了2D和3D情况下的绕射能量提取.

鉴于镜面反射与绕射能量成因存在明显差异，前者主要是第一菲涅尔带内的二次元波点震源产生的次生波的相干叠加，后者是绕射目标产生的次生波的叠加(滕吉文，1964；黄洪泽，1977). 本文在传统的Kirchhoff偏移(邹振等，2010)算子中引入反稳相滤波器(Moser and Howard，2008)，使满足Snell定律的镜面反射得到有效压制，不满足Snell定律的绕射能量得到保留，从而实现绕射波的提取；进一步考虑边缘绕射特有的极性反转现象，在成像过程中通过校正极性实现边缘绕射真正成像. 最后通过对理论模型合成数据和实际地震资料的绕射波成像试处理，验证本文方法的正确性、适应性和有效性. 1 边缘绕射波

图 1展示了常速介质v中的一个直角楔形体及相应的地震观测方式，XS和XR分别为震源和接收点位置，XCMP为共中心点，XD和ZD是地下边缘绕射点的横纵坐标，XB表示几何阴影区边界(即反射波在几何近似意义下的中断点).

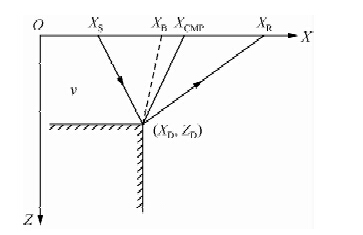图 1 边缘绕射示意图 Fig. 1 Edge diffraction and the geometry of the observational system

由菲涅尔绕射积分表示的统一渐进公式(Klem-Musatov，1994)推导得边缘绕射波表达式为

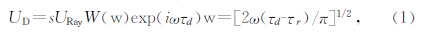
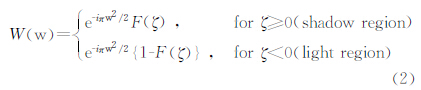
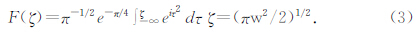
其中，URay表示应用射线方法在阴影区边界计算的反射波场(假设反射界面无限大). 当观测点位于阴影区(XB右边)时，s=1，当观测点位于照明区(XB左边)时，s=-1. τd表示绕射波旅行时，τr表示源自真正镜面反射点(照明区)的旅行时或源自假想反射点(阴影区)的反射波旅行时，ω为圆周频率，W表示衰减函数，表达式为

其中，F(ζ)表示菲涅尔积分：

分析公式(1)可知边缘绕射波在阴影区和照明区的边界(XB处)发生极性反转：在阴影区(XB右边)绕射波和边缘处的反射波极性相同，在照明区(XB左边)绕射波和反射波极性相反. 所以，边缘绕射波的极性反转特征是它区别于反射波的重要特征，可以用于边缘识别.

公式(2)所示的衰减函 数描述了边缘绕射波的振幅衰减特征：随着观测点到阴影区边界点距离的增加，边缘绕射波的振幅快速衰减，在阴影区边界处(即τd-τr=0)绕射振幅达到最大值，且为该点处反射振幅的一半(Trorey，1970).

综上，边缘绕射波在阴影区边界处发生极性反转，常规偏移方法往往将该类波压制，我们可以通过极性校正成像边缘绕射. 赵惊涛等(2011)详细阐述了边缘绕射波的成因及其动力学特征，通过分析绕射系数曲线在共炮点和共偏移距观测系统中的振幅变化特征得出：共偏移距剖面中边缘绕射波的振幅最大值和极性反转均出现在绕射点在地表投影处. 图 2为对图 1示意的直角楔形模型正演的零偏移距剖面，可以看出绕射波以极小点为中心，左右两支极性相反(黑色箭头所指). 因此，在共偏移距剖面中，边缘绕射波的极性校正相对简单，只需使绕射曲线的任意一支乘负一即可. 需要指出的是，本文研究的边缘绕射波不同于小尺度地质体的散射波，点散射波没有极性反转特征，也就是说极性校正方法仅能成像边缘绕射.

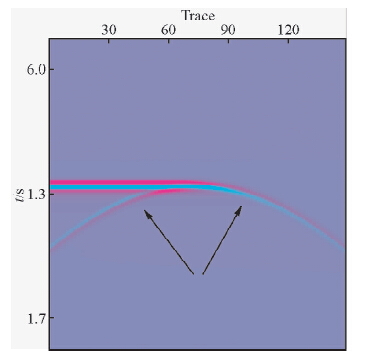图 2 边缘绕射极性反转示意图 Fig. 2 Polarity reversal of edge diffraction (indicated by the arrows)
2 反稳相滤波器

二维观测系统下，源自光滑反射界面上的镜面反射遵循Snell定律：入射射线和反射射线与界面法线共面，入射角等于反射角；源自界面边界(或不平滑界面)的绕射不满足Snell定律，出射射线可以沿着测线所在平面内的任意方向(Moser，2011；Sturzu et al.，2013). 图 3所示为上述两种情况下的射线路径示意图，其中黑色垂线表示界面法线，绿色射线表示入射射线，蓝色射线表示出射的镜面反射，红色射线表示绕射. 绕射波场提取的目的：将全波场中的镜面反射(图 3中蓝色射线)压制，将剩余波场(图 3中红色射线)作为绕射能量. 为此，本文引入如下函数：

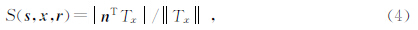
其中，Tx表示射线旅行时T(s，x，r)关于成像点横向位置x的偏导数，n 表示每个成像点处的界面法线. 该函数表示成像点处入射射线和出射射线的等分线与界面法线的夹角的余弦值. 对于镜面反射(图 3中蓝色射线)，界面法线正好是入射和反射射线的等分线，二者夹角为零度，上述函数达到最大值1；对于镜面反射之外的绕射(图 3中红色射线)，入射线和出射线的等分线与界面法线的夹角均不为零度，上述函数小于1.
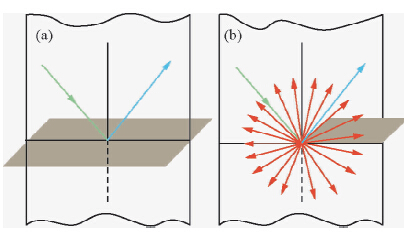图 3 射线路径示意图(a)镜面反射；(b)边界绕射. Fig. 3 Schematic illustration of the ray path (a)Specularity reflection；(b)Edge diffraction.

在高频近似下，只需将令(4)式等于1的能量压制，即可得到分离后的绕射能量. 然而，实际地震数据频带有限，地面某点观测到的反射能量是地下以镜面反射点为中心的菲涅尔带内的无数二次元波点震源的波场之和. 根据以上分析，构建如下滤波器(图 4所示)：

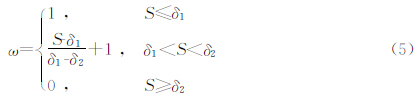
其中，S为(4)式所示函数，δ1和δ2为两个阈值，与地震频带有关，用于控制菲涅尔带的大小，δ1为绕射能量保留上限，δ2(1附近小于1的值)为镜面反射压制下限，二者之间为过渡区域. 与Bleistein(1987)，Schleicher等(1997)用于加强镜面反射的稳相滤波器相反，(5)式所示滤波器将菲涅尔带内的镜面反射压制，将剩余能量作为绕射，为此把该滤波器叫做反稳相滤波器.
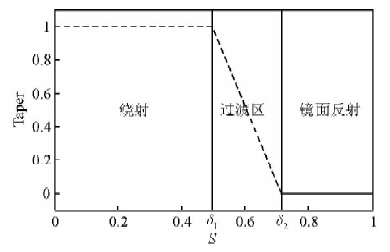图 4 反稳相滤波权函数 Fig. 4 Anti-stationary phase filtering weighting function
3 局部倾角估计

应用(5)式构建的反稳相滤波器需要获取地下每个成像点处的反射界面倾角信息(即4式中的界面法线 n). 在时间域可以将局部平面同相轴看作满足波动方程的平面波解，从而实现反射界面倾角估计.本文采用Fomel(2002)提出的平面波解构滤波方法从全波场成像剖面中求取反射界面倾角信息.

平面波解构滤波器利用局部平面波叠加来表征地震数据，可以被看作频空域(F-X)预测误差滤波器的时空域(T-X)模拟，能较好的估计平滑连续同相轴的局部倾角信息.根据局部平面波的物理模型，将如下的局部平面波微分方程作为平面波解构滤波器的理论基础：

其中，P(t，x)表示波场；σ为同相轴局部斜率：

(1)当局部斜率σ为常数时，方程(6)的通解为

其中，f(x)表示任意波形，方程(7)为平面波的数学描述.

(2)当局部斜率σ独立于t时，将式(6)变换到频率域可得频域一般解为

在F-X域平面波可以通过如下的两项预测误差滤波器得出

其中，a0=1，a1=-eiωσ.将该滤波器表示为Z变换的形式，并进一步分解为多个两项滤波器的乘积：

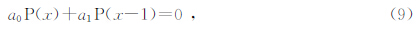
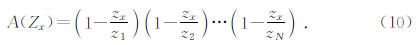
(3)当局部斜率σ随时间和空间都变化时，需重新变换到时间域寻找相移算子(8)和平面预测滤波器(9)的类似表达. 鉴于平面波传播的总能量保持不变，可以在时间域利用全通数字滤波器模拟该特性.在Z变换域，该过程表示为

其中，Px(Zt)表示相应地震道的Z变换，B(Zt)/B(1/Zt)为相移算子eiωσ的全通滤波近似. B(Zt)的系数可由相移滤波算子在低频时的频率响应拟合获得. 下式为用 Taylor级数展开求得的三点中心滤波器：

同时考虑时空两个方向上的变化，得到2D预测滤波器：

为了避免多项式除法，Fomel将式(13)所示滤波器进行改进得

由式(12)知C(Zt，Zx)为局部倾角σ的函数 C(σ)，则局部倾角估计问题可转化为如下的最小二乘问题：

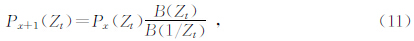
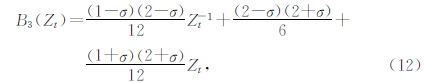
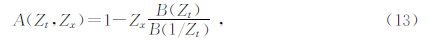
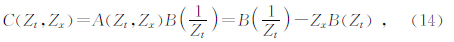
利用(15)式可从全波场成像结果中估计反射界面的倾角信息，进一步利用该倾角信息构建反稳相滤波器. 4 基于反稳相滤波的绕射成像

基于绕射叠加理论，Kirchhoff偏移将偏移孔径内所有地震道上满足双平方根走时关系的散射能量聚焦求和得到全波场成像剖面I(t，x)：

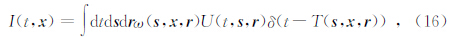
其中，U(t，s，r)表示全波场叠前数据，T(s，x，r)表示由双平方根方程计算的双程旅行时(程玖兵等，2009).引入权函数ω(s，x，r)可以使Kirchhoff偏移应用于不同目的：当ω(s，x，r)=1时，上式即古典的绕射叠加偏移，得到全波场成像结果；将(4)式作为权函数引入(16)式即可实现旨在突出镜面反射的稳相偏移(Bleistein，1987；Schleicher et al.，1997)；本文将第二部分求得的反稳相滤波器(5式所示)作为权函数，通过压制镜面反射能量实现绕射偏移成像.

综上所述，基于反稳相滤波的绕射成像包括以下三步：

(1)利用(16)式(ω(s，x，r)=1)得到全波场Kirchhoff叠前时间偏移剖面I(t，x)；

(2)应用第三部分所述的平面波解构滤波方法从I(t，x)中提取每个成像点处的反射界面倾角信息；

(3)将上一步估计的倾角信息作为输入构建(5)式所示的反稳相滤波器，把该滤波算子作为(16)式的权函数即可实现最终的绕射目标成像. 5 模型试算 5.1 凹陷模型

为了验证本文方法的正确性和有效性，采用图 5所示的凹陷模型对算法进行测试. 模型含有三个水平层和一个凹陷层，横向1001个CDP点，纵向301个采样点，纵横向采样间隔分别为10 m、5 m. 观测系统为中间放炮两边接收，炮间距20 m，最大偏移距1500 m，道间距10 m. 凹陷两翼的四个拐点是我们关注的绕射目标. 将(16)式中的权函数设为1得到全波场成像结果示于图 6a，图 6b所示为利用平面波解构滤波技术由全波场成像结果估计得到的同相轴局部斜率剖面，利用该倾角信息，构建反稳相滤波器，同时应用极性校正技术得到最终的绕射成像结果(图 6c).对比波场分离前后的偏移剖面可知：在绕射成像结果(图 6c)中，来自水平反射层和凹陷底部水平层的镜面反射能量全部被压制，凹陷两翼倾斜界面的大部分成像能量被压制；我们重点关注的凹陷两翼四个拐点得到很好的成像，另外，在两翼还保留有一系列能量点，分析知，由于数值正演对模型离散会在倾斜界面上引入许多小规模不连续，这些不连续体会产生丰富的绕射波，图 6c同样能把该类微小绕射目标清晰地刻画出来，从而验证了本文方法的正确性和可行性.

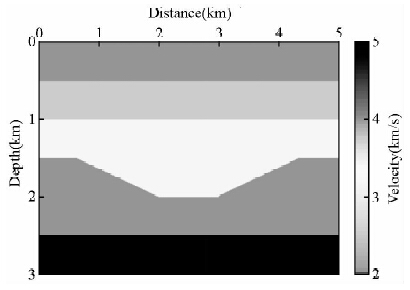图 5 凹陷模型速度场 Fig. 5 Interval velocity field of sag model

图 6 (a)全波场成像；(b)同相轴斜率估计剖面；(c)绕射波成像 Fig. 6 (a)Full wave-field image；(b)Slope estimation section；(c)Diffraction image
5.2 断层模型

针对边缘绕射成像设计了图 7所示的断层模型，速度模型包含一个大的正断层，另外，反射层上发育许多小断阶，上述断层或断阶的边界产生的边缘绕射波是本文成像目标. 模型横向1000个CDP点，纵向180个采样点，纵横向间距均为5 m. 采用声波方程高阶有限差分正演炮记录，共记录了350炮数据，每炮151道，道间距10 m，时间采样间隔为0.4 ms. 图 8a为该模型全波场叠前时间偏移成像结果，可以看出，反射与绕射在偏移剖面上共存，受强反射掩盖，相对弱的绕射能量不易识别，某些绕射目标定位不准. 图 8b为仅应用反稳相滤波器得到的绕射波成像结果，镜面反射得到了很好的压制，断阶边界附近的绕射能量保留下来. 然而，由于没有考虑边缘绕射的极性反转，图 8b中保留的能量并非真正的边缘绕射成像结果. 图 8c为仅进行极性校正后得到的成像结果，可以看出应用极性校正后，平缓的反射能量得到一定程度的压制，最主要的是边缘绕射能量同相叠加，很好的收敛于边界点，实现了最佳的边缘绕射成像. 同时应用反稳相滤波器和极性校正技术得到的绕射波成像结果示于图 8d，可以看出反稳相滤波器使镜面反射得到最大限度的压制，极性校正技术使边缘绕射能量真正成像，最后的绕射成像结果分辨率显著提高，边界绕射点成像位置精确. 为了阐明极性校正技术对边缘绕射成像的改进效果，我们对成像结果中小断阶边界所在区域放大后进行比较分析. 图 9所示为区域Ⅰ(图 8a示)的对比分析，(a)(b)(c)(d)分别为：全波场成像结果、反稳相绕射波成像结果(未应用极性校正)、仅应用极性校正的绕射波成像结果、反稳相绕射波成像结果(应用极性校正). 通过对比可知：仅应用反稳相滤波器的绕射成像结果(9b)可以很好地压制镜面反射，但是该方法只是把断阶附近的能量保留下来，这些能量并未很好的收敛，横向分布范围相对较大，据此不能精确定位断阶边界；仅应用极性校正的绕射成像结果(9c)中，断阶绕射很好地收敛于边界位置，绕射能量相对增强(白色虚线箭头所指)，与此同时镜面反射也得到一定程度压制，但是压制效果并不好；同时应用反稳相滤波器和极性校正技术得到的绕射成像结果(9d)中，反稳相滤波器最大限度地压制镜面反射，极性校正技术使边界绕射能量完全收敛，从而使断阶边界的识别精度更高. 与图 9相同，图 10对区域Ⅱ(图 8a示)的对比分析进一步验证了上述分析的正确性.

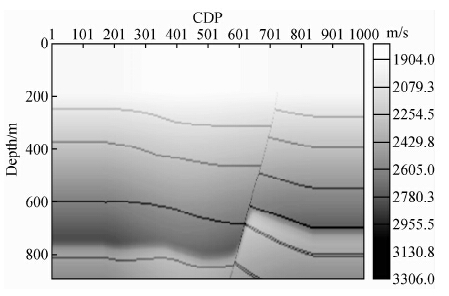图 7 断层模型速度场 Fig. 7 Interval velocity field of fault model

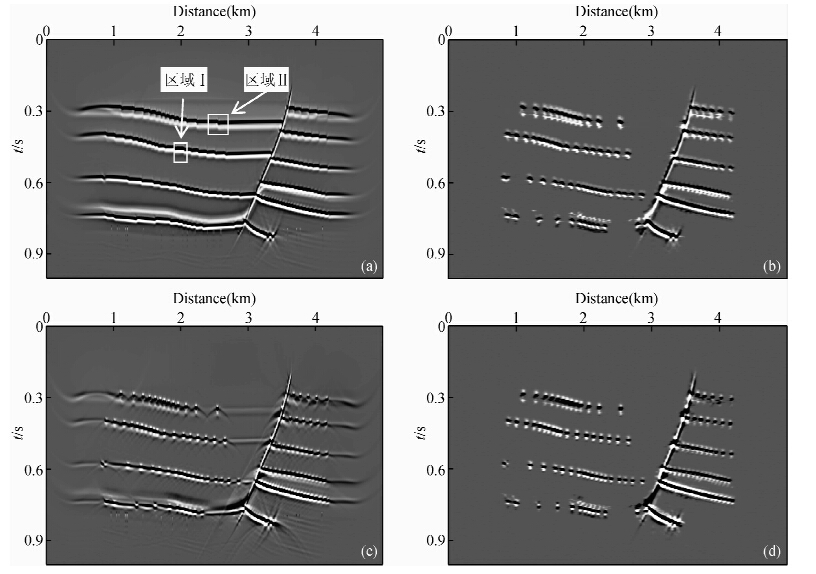图 8 (a)全波场成像结果；(b)反稳相绕射波成像结果(未应用极性校正)；(c)极性校正绕射波成像结果；(d)反稳相绕射波成像结果(应用极性校正) Fig. 8 (a)Full wave-field image；(b)Diffraction image obtained using anti-stationary phase filtering only；(c)Diffraction image obtained using polarity correction only；(d)Diffraction image obtained using both anti-stationary phase filtering and polarity correction technique

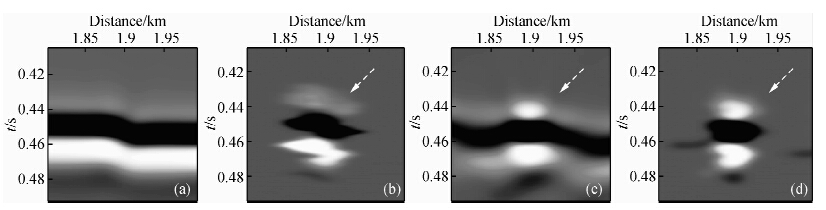图 9 断层模型不同成像结果的区域Ⅰ对比(a)全波场成像结果；(b)反稳相绕射波成像结果(未应用极性校正)；(c)极性校正绕射波成像结果；(d)反稳相绕射波成像结果(应用极性校正). Fig. 9 Comparison for small zoneⅠof different image (a)Full wave-field image;(b)Diffraction image obtained using anti-stationary phase filtering only；(c)Diffraction image obtained using polarity correction only；(d)Diffraction image obtained using both anti-stationary phase filtering and polarity correction technique.

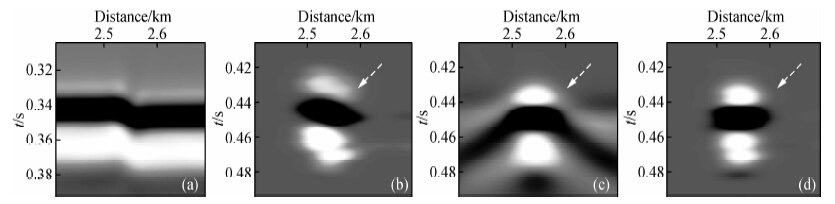图 10 断层模型不同成像结果的区域Ⅱ对比(a)全波场成像结果；(b)反稳相绕射波成像结果(未应用极性校正)； (c)极性校正绕射波成像结果；(d)反稳相绕射波成像结果(应用极性校正). Fig. 10 Comparison for small zoneⅡof different image (a)Full wave-field image；(b)Diffraction image obtained using anti-stationary phase filtering only；(c)Diffraction image obtained using polarity correction only；(d)Diffraction image obtained using both anti-stationary phase filtering and polarity correction technique.

为了进一步阐述绕射成像有助于提高地震解释的精度，本文将反射层上发育的小断阶的成像结果进行局部放大显示. 图 11a为波场分离前的局部放大图，图 11b为仅应用反稳相滤波器得到的局部放大结果，图 11c为同时应用反稳相滤波器和极性校正技术得到的局部放大结果. 对比可知：仅应用反稳相滤波器得到的结果(图 11b)中，镜面反射得到很好的压制，但是边缘绕射并未完全收敛，致使绕射能量横向分布范围大，不能准确的定位断阶边界，两个相邻较近的小断阶不易区分；同时应用两种技术的成像结果(图 11c)不仅很好的压制了反射能量，而且实现了边缘绕射的真正成像，绕射成像结果分辨率高，有助于精确定位断阶边界. 综上，同时应用反稳相滤波器和极性校正技术可以实现边缘绕射的真正成像，显著改善成像分辨率，进而提高地震解释精度. 值得注意的是，图 8d中的绕射波成像结果中，大尺度断层面并非绕射目标，本文出于两点考虑将其保留：(1)、彻底压制陡倾界面也会使绕射能量损失较大；(2)、该断层面同样可以为解释人员提供重要的地下信息.

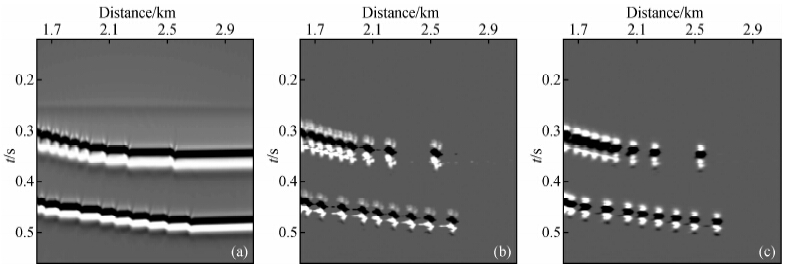图 11 断阶局部放大示例(a)全波场成像结果；(b)反稳相绕射波成像结果(未应用极性校正)；(c)反稳相绕射波成像结果(应用极性校正). Fig. 11 Zoom-in view of discontinuities(a)Full wave-field image;(b)Diffraction image obtained using anti-stationary phase filtering only；(c)Diffraction image obtained using both anti-stationary phase filtering and polarity correction technique.
5.3 实际资料

为了验证本文方法对实际资料的适应性，对Claerbout(2008)所用的墨西哥湾数据进行测试，该数据共250炮，每炮24道，时间采样间隔4 ms. 图 12a所示为该资料的全波场成像结果，几条断层隐约可见(红色虚线所示)；图 12b为同时应用反稳相滤波器和极性校正得到的边缘绕射波单独成像结果，由图可见：大部分反射能量压制后，边界绕射能量相对增强，几条断层清晰可见.

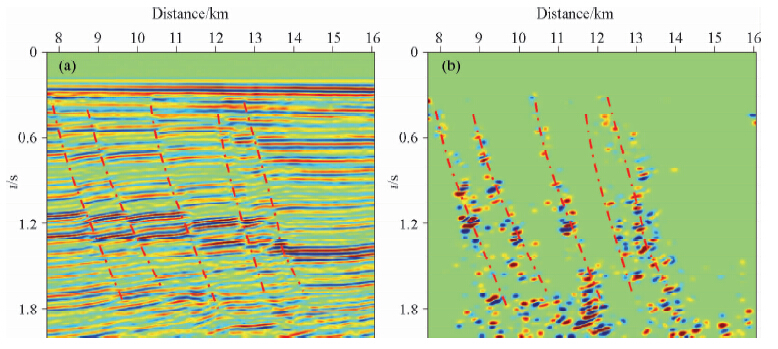图 12 实际资料(a)全波场成像；(b)绕射波成像. Fig. 12 Field data set (a)Full wave-field image；(b)Diffraction image.
6 结 论 6.1     本文通过在传统的Kirchhoff偏移算子中引入反稳相滤波器，使满足Snell定律的镜面反射得到有效压制，绕射能量得到保留；进一步考虑边缘绕射特有的极性反转现象，在成像过程中通过校正极性实现边缘绕射真正成像，得到的绕射波成像结果分辨率高，有助于断层、尖灭等小尺度地质不连续体的准确识别.模型数据和实际资料处理结果也进一步验证了本文方法的正确性和适应性.

6.2     本文所述的反稳相滤波技术可以有效压制镜面反射，包括大倾角反射界面(图 6c所示的断层两翼)，实际操作中可以通过控制(5)式中的阈值实现不同程度的反射压制. 图 8d中大尺度正断层产生的断面波本不属于绕射能量，但保留其可让解释人员直观地识别此处发育的大断层. 当然，如果彻底压制陡倾断面，绕射能量也会得到较大程度损失. 笔者认为，绕射和反射本没有清晰的划分界线，现有的绕射波分离方法大多是通过压制镜面反射能量来突出绕射，并不能实现二者的完全分离.

6.3     本文所述的极性校正技术可以使边缘绕射很好的收敛，实现真正的绕射成像. 然而，由于极性反转是边缘绕射特有的，本文局限于成像边缘绕射点. 许多学者根据尺度大小将小尺度散射体也归为绕射目标，然而由于点散射波没有极性反转特征，本文方法对该类目标并不适用. 事实上，这类小尺度散射体同样携带了地下的高分辨率信息，尤其在我国西部广泛分布的碳酸盐岩地层中，溶洞储集体通常表现为小尺度散射目标. 因此，如何实现小尺度不连续体和小尺度散射目标同时成像，使最后的绕射成像结果能很好地服务于生产意义重大.

6.4     绕射本质上是三维现象，与反射不同，源自绕射目标的能量向各个方向激发，如果能将各个方向的绕射能量都聚焦，绕射成像效果会更佳. 因此，在下一步的研究过程中，我们将尝试将本方法推广到三维情况.

致 谢 感谢审稿专家提出的宝贵修改意见和编辑部老师的帮助！
参考文献
[1] Asgedom E G,Gelius L J,Austeng A, et al. 2011. A new approach to post-stack diffraction separation[C]. SEG Expanded Abstracts,pp. 3861-3865,doi: 10.1190/1.3628011.
[2] Bai Y,Sun Z,Chen L, et al. 2011. Seismic Diffraction Separation in 2D and 3D Space[C]. 73rd EAGE Conference& Exhibition.
[3] Bansal R, Imhof M. 2005. Diffraction enhancement in prestack seismic data[J]. Geophysics,70(3): V73-V79,doi:10.1190/1.1926577.
[4] Berkovitch A, Belfer I, Hassin Y,et al. 2009. Diffraction imaging by multifocusing[J]. Geophysics,74(6): WCA75-WCA81,doi:10.1190/1.3198210.
[5] Bleistein N. 1987. On the imaging of reflectors in the earth.Geophysics52, 931-942.
[6] Cheng J B, Wang N, Ma Z T. 2009. Table-drive 3-D angle-domain imaging approach for Kirchhoff prestack time migration[J]. Chinese J. Geophys.(in Chinese), 52(3):792-800.
[7] Claerbout J F, Green I. 2008. Basic earth imaging[M]. Stanford University.
[8] Fomel S. 2002. Applications of plane-wave destruction filters[J]. Geophysics,67(6):1946-1960,doi: 10.1190/1.1527095.
[9] Fomel S,Landa E,Taner M T. 2007. Poststack velocity analysis by separation and imaging of seismic diffractions[J]. Geophysics,72(6):U89-U94,doi:10.1190/1.2781533.
[10] Gray,S. 2005. Gaussian beam migration of common-shot records[J]. Geophysics,70(4):S71-S77.
[11] Hagedoorn J G. 1954. A process of seismic reflection interpretation [J]. Geophysical prospecting,2(2): 85-127.
[12] Hill N R. 2011. Prestack Gaussian-beam depth migration[J]. Geophysics,66(5):1240-1250.
[13] HUANG HONG-ZE. 1977.THE MECHANISM OF DIFFRACTED WAVES. Chinese J. Geophys. (in Chinese), 20(1):81-88.
[14] Huang J P,Li Z C,Kong X,et al. 2012. The review of the wave field separation method about reflection and diffraction based on the PWD[J]. Progress in Geophysics (in Chinese),27(6): 2499-2510,doi: 10.6038/j.issn.1004-2903.2012.06.025.
[15] Kanasewich E R,Phadke S M. 1988. Imaging discontinuities on seismic section[J]. Geophysics,53:334-345,doi:10.1190/1.1442467.
[16] Khaidukov V,Landa E,Moser T J. 2004. Diffraction imaging by focusing-defocusing: An outkook on seismic superresolution[J]. Geoghysics,69(6):1478-1490,doi:10.1190/1.1836821.
[17] Klem-Musatov, K. 1994. Theory of seismic diffractions: Soc. Expl.Geophys.
[18] Klokov A, Baina R,Landa E,et al. 2010. Diffraction imaging for fracture detection: synthetic case study[C]. SEG Exoanded Abstracts,pp:3354-3358,doi: 10.1190/1.3513545.
[19] Kong X,Li Z C, Huang J P,et al. 2012. Diffraction objective imaging based on plane wave record[J]. Oil Geophysical Prospecting (in Chinese),47(4):674-681.
[20] Krey T. 1952. The significance of diffraction in the investigation of faults[J]. Geophysics,17(4): 843-858,doi: 10.1190/1.1437815.
[21] Landa E,Fomel S,Reshef M. 2008. Separation imaging and velocity analysis of seismic diffractions using migrated dip-angle gathers[C]. SEG Expanded Abstracts,2176-2180,doi:10.1190/1.3059318.
[22] Landa E,Shtivelman V,Gelchinsky B. 1987. A method for detection of diffracted waves on common-offset section[J]. Geophysical Prospecting,35(4):359-373.
[23] Li X F,Huang J,Li Z C,et al. 2013. The Research of Diffraction Migration Velocity Analysis Method[C]. 75th EAGE Conference & Exhibition incorporating SPE EUROPEC.
[24] LIU Yu-jin,LI Zhen-chun,HUANG Jian-ping,et al. 2013. Prestack time migration velocity analysis and imaging of seismic diffractions. Progress in Geophys.(in Chinese),28(6):3022-3029,doi:10.6038/pg20130625.
[25] Moser T J, and Howard C B. 2008. Diffraction imaging in depth, Geophysical Prospecting, 56, 627-641.
[26] Moser T J. 2011. Edge and Tip Diffraction Imaging in Three Dimension, 73rd EAGE Conference Vienna, Extended Abstracts.
[27] Nowak E J,Imhof M G. 2004. Diffractor localization via weighted Radon transforms[C]. SEG Expanded Abstracts,2108-2111,doi:10.1190/1.1851199.
[28] Reshef M,Landa E. 2009. Post-stack velocity analysis in the dip-angle domain using diffractions[J]. Geophysical Prospecting,57(5):811-821.
[29] Schleicher J., Hubral P., Tygel M. and Jaya M.S. 1997. Minimum apertures and Fresnel zones in migration and demigration. Geophysics 62, 183-194.
[30] Sturzu I., Popovici A.M. 2013. Specularity Gathers for Diffraction Imaging, 75th EAGE Conference London, Extended Abstracts.
[31] Taner M T,Fomel S,Landa E. 2006. Separation and imaging of seismic diffractions using plane-wave decomposition[C]. SEG Expanded Abstracts,2401-2405, doi: 10.1190/1.2370017.
[32] Trorey, A.W. 1970.A simple theory for seismic diffractions, Geophysics 35, 762-784.
[33] Zhao J T,Wang Z L,Yu C X. 2011. Edge diffraction wave and its dynamic detection methods in seismic exploration. Progress in Geophys.(in Chinese),26(1):194-206,DOI:10.3969/j.issn.1004-2903.2011.01.021.
[34] Zhu S W, Li P, Ning J R. 2013. Reflection/diffraction separation with a hybrid method of local dip filter and prediction inversion. Chinese J. Geophys. (in Chinese), 56(1):280-288,doi:10.6038/cjg2013 0129.
[35] Zhu Xiao-San,Wu Ru-Shan. 2010. Imaging diffraction points using the local image matrices generated in prestack migration[J]. Geoghysics,75(1):S1-S9,doi: 10.1190/1.3277252.
[36] Zou Z,Liu H,Liu H W. 2010. Common-angle gathers based on Kirchhoff pre-stack time migration. Chinese J. Geophys.(in Chinese),53(5):1207-1214,DOI:10.3969/j.issn.0001-5733.2010.05.023.
[37] 程玖兵,王楠,马在田. 2009. 表驱三维角度域Kirchhoff叠前时间偏移成像方法[J]. 地球物理学报,52(3):792-800.
[38] 黄洪泽. 1977. 论绕射波机制. 地球物理学报,20(01):81-88.
[39] 黄建平,李振春,孔雪,等. 2012. 基于PWD的绕射波波场分离成像方法综述[J]. 地球物理学进展,27(6): 2499-2510,doi:10.6038/j.issn.1004-2903.2012.06.025.
[40] 孔雪,李振春,黄建平,等. 2012. 基于平面波记录的绕射目标成像方法研究[J]. 石油地球物理勘探,47(4):674-681.
[41] 刘玉金,李振春,黄建平,等. 2013. 绕射波叠前时间偏移速度分析及成像. 地球物理学进展, 28(6):3022-3029,doi:10.6038/pg20130625.
[42] 滕吉文. 1964. 绕射波的动力学特性与介质物理参数间的关系. 地球物理学进展,13(2):128-147.
[43] 赵惊涛,王真理,于彩霞. 2011. 地震勘探中的边缘绕射波及其动力学识别方法. 地球物理学进展,26(1):194-206,DOI:10.3969/j.issn.10042903.2011.01.021.
[44] 朱生旺,李佩,宁俊瑞. 2013. 局部倾角滤波和预测反演联合分离绕射波. 地球物理学报,56(1):280-288,doi:10.6038/cjg20130129.
[45] 邹振,刘洪,刘红伟. 2010. Kirchhoff叠前时间偏移角度道集. 地球物理学报,53(5):1207-1214, DOI:10.3969/j.issn.0001-5733.2010.05.023.