地球物理学进展  2015, Vol. 30 Issue (2): 581-585   PDF    
引用本文
石颖, 柯璇, 张莹莹. 2015. 逆时偏移边界条件与存储策略分析[J]. 地球物理学进展, 30(2): 581-585, doi: 10.6038/pg20150214  
SHI Ying, KE Xuan, ZHANG Ying-ying. 2015. Analyzing the boundary conditions and storage strategy for reverse time migration. Progress in Geophysics, 30(2): 581-585, doi: 10.6038/pg20150214   
逆时偏移边界条件与存储策略分析
石颖1,2, 柯璇1, 张莹莹1    
1. 东北石油大学 地球科学学院, 大庆 163318;
2. 黑龙江省普通高校科技创新团队“断层变形、封闭性及与流体运移”, 大庆 163318
收稿日期: 2014-12-10 修回日期: 2015-1-8 .
基金项目：国家“863”高技术研究发展计划项目(2012AA061202)、国家自然科学基金(41474118)和东北石油大学研究生创新科研项目(YJSCX2014-005NEPU)联合资助.
作者简介：石颖,女,1976年生,博士,教授,主要从事地震资料处理方面的研究.(E-mail:shiyingdqpi@163.com)
摘要：地震波场模拟是叠前逆时偏移方法的核心计算单元, 因此, 边界条件和存储方案的选择是高精度以及高效率逆时偏移算法不可回避的问题.本文就随机边界条件和吸收边界条件在逆时偏移算法中的应用效果以及相应的四种存储策略展开具体分析, 给出了不同存储策略下的计算成本和存储量需求.文中优选随机边界条件和吸收边界条件的有效边界存储方案, 引入GPU并行加速技术对SEG起伏地表模型进行测试, 详细讨论分析了两种方法的计算效率和计算精度.测试表明, 随机边界存储的计算成本要低于有效边界存储的计算成本, 而受边界散射的影响, 随机边界逆时偏移在浅层伴有噪音干扰.针对具体数据情况, 合理地运用GPU加速技术、选择有效的边界条件以及存储方法, 是改善逆时偏移成像精度和效率的有效途径.
关键词： 逆时偏移     随机边界条件     吸收边界条件     存储    
Analyzing the boundary conditions and storage strategy for reverse time migration
SHI Ying1,2, KE Xuan1, ZHANG Ying-ying1    
1. Earth Science College of Northeast Petroleum University, Daqing 163318, China;
2. Science and Technology Innovation Team on Fault Deformation, Sealing and Fluid Migration, Daqing 163318, China
Abstract: Seismic wave field modeling is the computing core of pre-stack reverse time migration. Therefore, for improving the accuracy and computational efficiency of reverse time migration, effective boundary condition and storage strategies are the key factors. In this paper, we analyzed the application effect by reverse time migration and four kinds of storage strategies with random and absorbing boundary conditions, summarized the calculation cost and storage requirement for different boundary and storage strategies. We have tested the reverse time migration algorithm on SEG rugged topography model with random boundary condition and absorbing boundary condition with its efficient boundary storage scheme chosen, combined with GPU (Graphic Processing Unit) acceleration technology. The result shows that the computational cost of random boundary storage is lower than which of efficient boundary strategy, but affected by the boundary scattering, the reverse time migration profile with random boundary would get noise interference in shallow layers. The key scheme to improve the accuracy and computational efficiency of reverse time migration is choosing compatible boundary condition, storage strategy, and GPU acceleration technology according to the specific data.
Key words: reverse time migration     random boundary condition     absorbing boundary condition     storage    
0 引 言

逆时偏移成像(RTM)技术早在1983年被提出(Baysal等，1983; McMechan，1983；Whitmore等，1983)，受限于当时的硬件水平，该方法最初发展缓慢.近年来，伴随着计算机硬件和并行加速技术的飞速发展，以及其对复杂构造盐下成像的成功应用，逆时偏移方法备受关注.目前RMT算法研究已由声波理论发展为弹性波理论(Yan等，2012)，由各向同性介质发展为各向异性介质(Zhang等，2009)，由二维方法发展为三维，由单一有效波成像发展为全波场成像，由地面地震RTM扩展到井中地震RTM(刘诗竹等)，也有在偏移过程中考虑Q的思路(Deng和McMechan等，2008).与此同时，部分专家和学者从逆时偏移的实用性角度出发，致力于计算效率、存储策略以及边界条件等关键性技术研究.

随着GPU并行加速计算技术在地球物理领域的成功应用(李博，2009)，逆时偏移计算效率的提高迎来了新的契机，使其计算效率提高了一个数量级(李博，2010；刘红伟等， 2010a，b)，加快了逆时偏移由理论研究迈向实际应用的步伐.刘守伟等(2013)提出了GPU/CPU机群实现方案，对大数据逆时偏移计算有着指导意义.

当选用互相关成像条件进行RTM计算时，要获知同一时刻的下行震源波场和上行检波点波场值，但是二者传播方向相反，因此最直接的方法是事先存储震源或检波点波场的传播历史，这将要产生巨大的存储需求(Liu，2013)，因此目前大多仅保存部分震源波场，在检波点波场反传的过程中，再利用保存的部分震源波场恢复其传播历史(G Nguyen，2015)，如仅保存最后二个时刻震源波场的随机边界条件方法(Robert C，2009)，仅保存部分时刻震源波场的最优检查点方法(Symes，2007)，仅记录未衰减单层波场的吸收边界波场存储方法(王保利等，2012；胡昊，2013)等.在这些方法中，波场模拟所用边界条件与波场存储二者之间相互依存制约，如何优选方法并最大程度地兼顾二者的优势，是获得高精度和高效率逆时偏移成像的研究重点之一.

本文将重点对随机边界条件、PML吸收边界条件及与之对应的存储策略进行研究.结合逆时偏移方法原理，分析不同边界条件对成像效果的影响，并进一步探讨不同存储策略在逆时偏移计算量、存储量上的差异，最后通过模型算例对比分析上述方法的实际应用效果. 1 随机边界条件与存储

为了兼顾考虑逆时偏移计算的波场存储需求，Clapp(2009)提出一种随机边界思想，在速度场外围加入随机速度层，并将其用于逆时偏移激发点波场模拟计算中，故称为随机边界条件.设计速度值为2000 m/s的匀速速度场，并将其周围加入随机边界，如图 1所示.当地震波传播至边界处，部分波场向随机速度层传播，部分以随机漫反射的形式反射回波场内部.若在模型中央放置震源，即水平1.6 km，深度1.6 km处激发子波，得到850 ms的波场快照如图 2所示.

图 1 随机边界速度场Fig. 1 Velocity field with random boundary

图 2 随机边界波场快照Fig. 2 Snapshot with random boundary

由于边界处波场仅传播形式不同，波场能量信息并未衰减，因此在保存最大时刻波场信息的情况下，通过地震波传播的逆向计算即可获得正传历史时刻的波场.若将模型水平方向网格点数记为Nx，垂直方向网格点数记为Nz，边界网格点数均记为 B，时间方向的采样点数为Nt.以时间二阶差分为例，逆时偏移计算保存最大两个时刻的波场，所需存储量为 8(Nx+2B)(Nz+2B)字节，计算量为3Nt(Nx+2B)(Nz+2B).

2 吸收边界条件与存储

当利用吸收边界条件时，考虑在波场周围布置吸收衰减层，当地震波传至吸收层后，对其振幅进行平滑衰减，避免波反射现象，PML是一种常用的吸收边界条件.加入边界参数后的波动方程可表述为

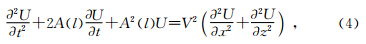
式中，A(l)为衰减系数.其分布趋势如图 3所示，波场内部衰减系数为0值(白色)，并且自内向外逐渐递增(白色过渡为黑色)，衰减强度逐渐增强.
图 3 衰减系数分布Fig. 3 Layout of attenuation coefficient

假定图 3所示的衰减系数分布在匀速2000 m/s的各向同性介质上，在水平方向1.6 km，垂直方向0.8 km处激发震源，观察传播时间至500 ms波场快照，波场传播至上边界吸收层后被逐步衰减.

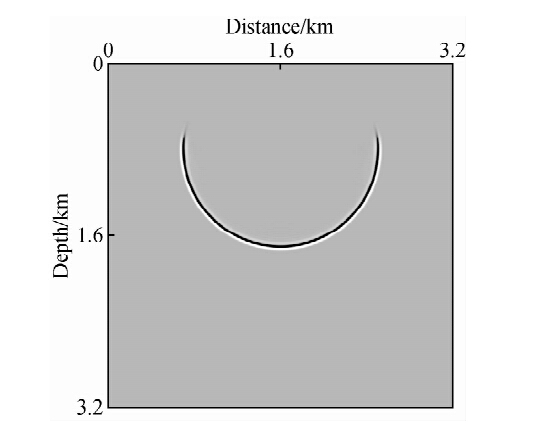图 4 PML边界波场快照Fig. 4 Snapshot with PML boundary

吸收边界条件的优势在于可有效降低边界反射干扰，但由于吸收边界区衰减了波场振幅，因此无法通过简单的逆向计算恢复正传波场，历史时刻波场信息依赖于存储，因此对吸收边界条件存储策略的制定也一直是学者们积极探索的问题.

目前吸收边界条件下的存储方案有多种，这里仅阐述分析常用的三种.

方案A： 全波场存储.将震源激发的每个时刻的正传波场存储于磁盘，互相关成像时，按时间点索引进行数据访问，该方法的计算量最小，为2Nt(Nx+2B)(Nz+2B)，但数据访问量巨大，为4NtNxNz字节，由于需受磁盘访问速度限制，耗时较多.

方案B： checkpointing检查点存储.在震源激发波场的正传过程中，每隔N个时刻建立一个检查点进行波场存储，在检波点波场反传并实现互相关成像时，从距离相关成像时刻之前最近的检查点波场进行正传模拟直至获得相关时刻点波场.该方法可将存储量压缩至方案一的1/N，但也在很大程度增加了计算量，为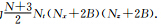.通过改变N值大小，可调节计算量与存储量的折中比例.

方案C： 有效边界存储.王保利等(2012)结合了上述两种方案的优势，提出了有效边界存储的方法，在激发点波场正传过程中，仅保存最后时刻以及内部波场边界外围有限层网格的波场信息，并在波场反传时作为边界条件获得准确的内部波场信息.有限边界存储方法如图 5所示，以时间二阶、空间十阶的有限差分为例，保存最后两个时刻A区域的波场与每时刻B区域的波场，在波场反向传播计算时，将对应时刻的B区域数据重新加载，即可获得每时刻A区域的波场信息.该方法计算量为2Nt(Nx+2B)(Nz+2B)+NtNxNz，其小于随机边界条件计算量，存储量为4L(Nx+Nz)Nt字节，其中L为波场的空间差分阶数.有效边界存储是目前吸收边界条件存储策略中较为有效的一种方案，在保证波场数值精度的基础上，不引入额外计算量，同时较大程度地降低了存储需求.

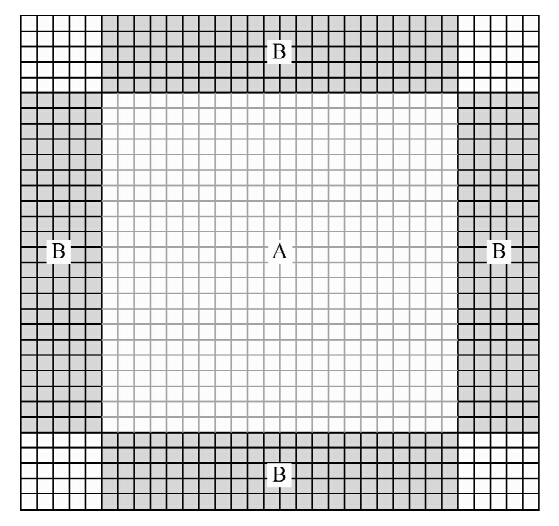图 5 有效边界存储Fig. 5 Efficient boundary storage
3 模型试算

从上文易知，随机边界条件和吸收边界条件的C存储方案可更好地节约存储空间.下面基于SEG起伏地表模型的局部数据进行测试，详细分析二种边界方法的计算效率和计算精度.截取模型数据的尺寸大小为：水平方向700个网格点，垂直方向600个网格点，速度模型如图 6所示.

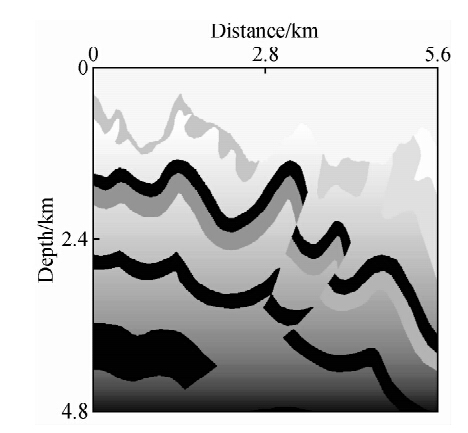图 6 SEG起伏地表模型(局部)Fig. 6 The SEG rugged topography model(local)

下面利用同一模型参数对两种方法进行对比测试.模型的水平及垂直网格间距均为8 m，时间采样率为0.5 ms，采样点数为8000，设置边界层厚度为100个网格点.震源激发采用了主频40 Hz的雷克子波，激发点位于地表居中位置(水平方向2.8 km)处，在0~5.6 km范围的地表，均匀布设700个检波点.本测试以GPU和CPU协同并行加速计算平台为测试计算环境.

基于上述给定的测试参数，对比分析随机边界和吸收边界条件C存储方案单炮计算的计算成本，测试结果如图 7所示.从图中可看出，若考虑总的计算成本，有效边界存储耗时多于随机边界存储方法.若详细分析计算过程，有效边界存储的额外耗时主要来源于边界存储，一是目前磁盘的读写效率低于处理器的计算效率，二是在激发点波场正传过程中，需要在每个时刻对边界有效波场进行截取保存；在激发点波场反传过程中，计算区域仅限于有效波场内部而无需考虑吸收边界层的计算，因此计算量略小；由于随机边界和吸收边界条件C存储方案的计算模式类似，所以在检波点波场反传和其他相关计算方面，二者计算时间大致相当.

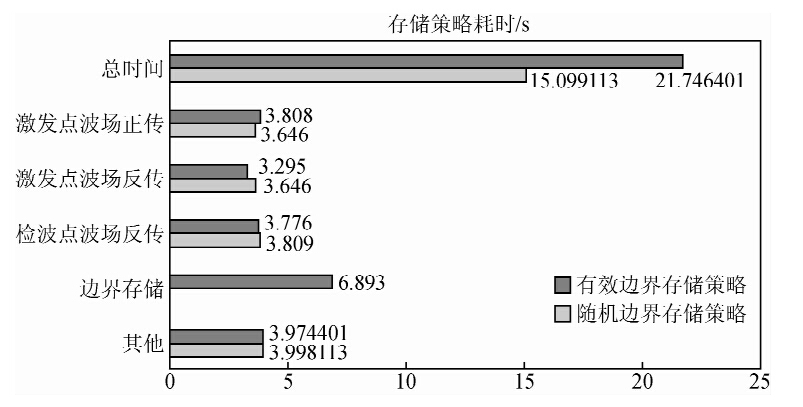图 7 有效边界和随机边界存储耗时对比Fig. 7 Time-consuming comparison between efficient boundary and r and om boundary

对图 6所示的SEG起伏地表模型，设计350炮震源激发，激发点自左至右均匀分布于地表，炮间距16 m，其他模型参数同上，测试两种不同存储方法的成像效果，图 8a为采用吸收边界条件C存储方案的逆时偏移剖面，图 8b为采用随机边界条件的逆时偏移剖面.对比观察看出，两种方法均能对地下构造准确归位成像，但受波场模拟产生的边界散射影响，相比于吸收边界偏移效果，随机边界逆时偏移在浅层边界处产生了较为明显的噪音干扰.

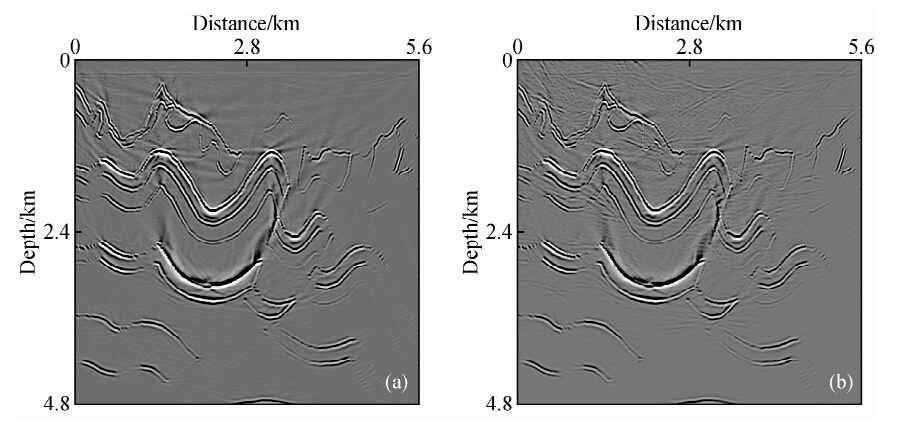图 8 不同存储方法的逆时偏移
(a)有效边界存储；(b)随机边界存储Fig. 8 Reverse time migration profile with different storage strategies
(a)Reverse time migration by efficient boundary storage；(b)Reverse time migration by r and om boundary storage.
4 结 论

本文对叠前逆时偏移计算中边界条件和存储策略的选取展开具体分析，阐述了两种常用边界条件，即随机边界条件和吸收边界条件，以及与其对应的多个存储策略的基本原理和计算成本.文中优选随机边界条件和吸收边界条件的有效存储方案，对SEG起伏地表模型进行测试，并分别从计算量、存储量和成像精度三方面进行了对比分析.有效边界存储更适用于存储能力优于计算能力的计算设备，随机边界存储反之，若仅从高精度成像的角度考虑，采用有效边界存储会获得相对满意的成像效果.

参考文献
[1] Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration[J]. Geophysics, 48(11): 1514-1524, doi: 10.1190/1.1441434.
[2] Clapp R G. 2009. Reverse time migration with random boundaries[C].//79rd Annual International Meeting, SEG Expanded Abstracts, 2809-2813.
[3] Deng F, McMechan G A. 2008. Viscoelastic true-amplitude prestack reverse-time depth migration[J]. Geophysics, 73(4):S143-S155.
[4] Five ways to avoid storing source wavefield snapshots in 2D elastic prestack reverse time migration. Geophysics, 80(1):S1-S18.
[5] Hu H, Liu Y K, Chang X, et al. 2013. Analysis and application of boundary treatment for the computation of reverse-time migration[J]. Chinese J. Geophys., (in Chinese), 56(6): 2033-2042, doi: 10.6038/cjg20130624.
[6] Li B, Liu G F, Liu H. 2009. A method of using GPU to accelerate seismic pre-stack time migration[J]. Chinese J. Geophys., (in Chinese), 52(1): 245-252.
[7] Li B, Liu H W, Liu G F, et al. 2010. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU[J]. Chinese J. Geophys., (in Chinese), 53(12): 2938-2943, doi: 10.3969/j.issn.0001-5733.2010.12.017.
[8] Liu H W, Li B, Liu H, et al. 2010a. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation[J]. Chinese J. Geophys., (in Chinese), 53(7): 1725-1733, doi: 10.3969/j.issn.0001-5733.2010.07.024.
[9] Liu H W, Liu H, Zou Z. et al. 2010b. The problems of denoise and storage in seismic reverse time migration[J]. Chinese J. Geophys., (in Chinese), 53(9): 2171-2180, doi: 10.3969/j.issn.0001-5733.2010.09.017.
[10] Liu H W, Ding R W, Liu L, et al. 2013. Wavefield reconstruction methods for reverse time migration[J]. Journal of Geophysics and Engineering, 10:1-6.
[11] Liu S Z, Shi Y, Guo X B. et al. 2014. Investigation on reverse-time migration of VSP data[J]. Progress in Geophysics. (in Chinese), 29(5):2211-2218, doi:10.6038/pg20140533.
[12] Liu S W, Wang H Z, Chen S C, et al. 2013. Implementation strategy of 3D reverse time migration on GPU/CPU clusters. Chinese J. Geophys., (in Chinese), 56(10): 3487-3496, doi: 10.6038/cjg20131023.
[13] McMechan G A. 1983. Migration by extrapolation of time-dependent boundary values[J]. Geophysical Prospecting, 31:413-420.
[14] Nguyen B D, McMechan G A. 2015.
[15] Symes W W. 2007. Reverse time migration with optimal checkpointing[J]. Geophysics, 72(5): SM213-SM221, doi: 10.1190/1.2742686.
[16] Wang B L, Gao J H, Chen W C, et al. 2012. Efficient boundary storage strategies for seismic reverse time migration[J]. Chinese J. Geophys., (in Chinese), 55(7): 2412-2421, doi: 10.6038/j.issn.0001-5733.2012.07.025.
[17] Wang W H, Ke X, Pei J Y. 2013. Application investigation of perfectly matched layer absorbing boundary condition[J]. Progress in Geophysics, (in Chinese), 28(5): 2508-2514, doi: 10.6038/pg20130529.
[18] Whitmore N D. 1983. Iterative depth migration by backward time propagation[C]. 53rd Annual International Meeting, SEG Expanded Abstracts, 382-385.
[19] Yan R, Xie X B. 2012. An angle-domain imaging condition for elastic reverse time migration and its application to angle gather extraction[J]. Geophysics, 75(5):S105-S115.
[20] 胡昊, 刘伊克, 常旭,等. 2013. 逆时偏移计算中的边界处理分析及应用[J]. 地球物理学报, 56(6): 2033-2042, doi: 10.6038/cjg20130624.
[21] 李博, 刘国峰, 刘洪. 2009. 地震叠前时间偏移的一种图形处理器提速实现方法[J]. 地球物理学报, 52(1): 245-252.
[22] 李博, 刘红伟, 刘国峰,等. 2010. 地震叠前逆时偏移算法的CPU/GPU实施对策[J]. 地球物理学报, 53(12): 2938-2943, doi: 10.3969/j.issn.0001-5733.2010.12.017.
[23] 刘红伟, 李博, 刘洪,等. 2010a. 地震叠前逆时偏移高阶有限差分算法及GPU实现[J]. 地球物理学报, 53(7): 1725-1733, doi: 10.3969/j.issn.0001-5733.2010.07.024.
[24] 刘红伟, 刘洪, 邹振,等. 2010b. 地震叠前逆时偏移中的去噪与存储[J]. 地球物理学报, 53(9): 2171-2180, doi: 10.3969/j.issn.0001-5733.2010.09.017.
[25] 刘诗竹, 石颖, 郭雪豹, 等. 2014. VSP数据逆时偏移方法研究[J]. 地球物理学进展, 29(5):2211-2218, doi:10.6038/pg20140533.
[26] 刘守伟, 王华忠, 陈生昌,等. 2013. 三维逆时偏移GPU/CPU机群实现方案研究[J]. 地球物理学报, 56(10): 3487-3496, doi: 10.6038/cjg20131023.
[27] 王保利, 高静怀, 陈文超,等. 2012. 地震叠前逆时偏移的有效边界存储策略[J].地球物理学报, 55(7): 2412-2421, doi: 10.6038/j.issn.0001-5733.2012.07.025.
[28] 王维红, 柯璇, 裴江云. 2013. 完全匹配层吸收边界条件应用研究[J]. 地球物理学进展, 28(5): 2508-2514, doi: 10.6038/pg20130529.