地球物理学进展  2015, Vol. 30 Issue (1): 466-470   PDF    
引用本文
朱常坤, 梁杏. 多参数层序地层的边缘最优智能划分算法及其应用[J]. 地球物理学进展, 2015, 30(1): 466-470, doi: 10.6038/pg20150169  
ZHU Chang-kun, LIANG Xing. An edge detection optimum intelligent division method and its application for multi-parameter log data. Progress in Geophysics, 2015, 30(1): 466-470, doi: 10.6038/pg20150169   
多参数层序地层的边缘最优智能划分算法及其应用
朱常坤1,2,3, 梁杏1,4     
1. 中国地质大学(武汉)环境学院, 武汉 430074;
2. 江苏省地质调查研究院, 南京 210018;
3. 国土资源部地裂缝地质灾害重点实验室, 南京 210018;
4. 中国地质大学(武汉)环境学院湿地演化与生态恢复湖北省重点实验室, 武汉 430074
收稿日期: 2014-08-06 修回日期: 2014-11-16 .
基金项目：国家重点基础研究发展计划“973”项目(2010CB428802)和国家自然科学基金项目(41272258)联合资助.
作者简介：朱常坤, 男, 1987年生, 地下水科学与工程专业硕士研究生, 主要从事三维地质建模及入渗补给科研工作. (E-mail:willing1104@163.com)
通讯作者：梁杏, 女, 1958年生, 教授, 博士生导师, 主要从事地下水流系统理论与工程水文地质方向的教学与科研工作. (E-mail:xliang@cug.edu.cn)
摘要：将最优分割、边缘检测与多种群遗传算法相结合, 设计了一种适用于多参数层序地层自动划分的边缘最优智能划分算法.该算法综合利用测井参数的Fisher比与表征测点奇异性的Lipschitz指数(Lipschitz Exponent, LE)构造优化指标;以钻孔参数测点为基因, 以有序测点组为染色体, 通过参数控制实现不同种群同时进行优化搜索, 采用移民算子沟通各种群协同进化;实现综合利用多参数测井数据求取最优化地层分界线.在河北平原第四纪地层岩性划分中的实际应用, 表明该方法的自动分层结果符合地质实际, 计算速度快, 分层效率高, 对河北平原山前冲积洪积、中部冲积湖积、东部冲积海积等不同沉积类型地层的划分工作都有较好适用性.
关键词： 层序地层     自动划分     边缘最优智能算法     旋回     奇异性    
An edge detection optimum intelligent division method and its application for multi-parameter log data
ZHU Chang-kun1,2,3, LIANG Xing1,4     
1. School of Environmental Studies, China University of Geosciences (Wuhan), Wuhan, Hubei 430074, China;
2. Geological Survey of Jiangsu Province, Nanjing 210018, China;
3. Key laboratory of Earth Fissures Geological Disaster, Ministry of Land and Resources, Nanjing 210018, China;
4. Hubei Key Laboratory of Wetland Evolution & Ecological Restoration, School of Environment Studies, China University of Geosciences, Wuhan 430074, China
Abstract: Sequence stratigraphy division is the important part of geological work, especially in the field of geologic modeling, inversion of sedimentary environment and mineral resources exploration. Well logs can be used for dividing a well (or a segment of it) into a group of sub-sections. In this paper, an edge detection optimum intelligent division method is designed for multi-parameter sequence stratigraphic division. The algorithm incorporates the Fisher optimal division and edge detection methods into Multi-Population Genetic Algorithm (MPGA). The optimization criterion involves the following steps. To begin with, Fisher Ratio and Lipschitz Exponent (LE), which respectively characterize the cycle and singularity of the measuring points, of the Logging parameters are utilized for optimization index constructing. Fisher ratio can be calculated by the sum of the deviation within and between layers, and LE can be calculated by Wavelet Transform Modulus Maxima (WTMM). Then logging measurement points are treated as genes and the group of ordered measurement points are regarded as chromosomes. In order to achieve different populations optimizing searching simultaneously, the parameters of crossover probability and mutation probability are controlled in a reasonable range. Meanwhile, immigrant operators are utilized for coevolving between various populations, which finally realize automatic dividing of sequence stratigraphy basing on multi-parameter logging data. This method mentioned before is applied on division of the Quaternary lithology in the Hebei Plain. It is shown that, the stratigraphic division results accord with the geologically fact. Moreover, the method proves faster and more efficient than the ordinary Fisher optimal division method in computation. It can be conclude that the edge detection optimum intelligent division method is highly applicable in Hebei Plain stratigraphic division of different sediment types, including piedmont area of diluvial alluvial plains, central area of alluvial lacustrine plain and eastern area of alluvial marine plain.
Key words: sequence stratigraphy     automated division     edge detection optimum intelligent algorithm     cycle     singularity    
0 引 言

地层划分与对比是地质工作的基础，也是矿产资源勘探(Shaaban and Ghoneimi， 2001；徐亚等，2007)、沉积环境反演(Wonik，2001；陈艇等，2013)和水文地质建模(程丹等，2007)等工作的重要组成部分.

传统的最优分割法通过极小化段内离差总和与段间离差总和的比值寻找分层方案，该方法易于理解并被广泛使用(刘伯土等，2000)，但忽略了测井曲线的形态信息，难以检测到突变点，而这些突变点往往是旋回变更、沉积间断和沉积环境的突变等在测井参数上的反应，是可能的地层界线(曹向阳等，2009).为了定量刻画各测点的奇异性，张振飞等(2009)通过计算某一指标在窗口两半的差异得到测点边缘隶属度，使用这种边缘检测算法得到的隶属度值受窗宽的影响，且正、负突变往往计算出不同的突变位置.近年来，小波技术在地层划分中得到了广泛应用(赵军龙和李娜，2008；任金锋等，2013).Pan等(2008)对测井数据综合使用傅里叶变换(Fourier transform，FT)和小波变换(wavelet transform，WT)方法实现地层界面识别.深入研究发现(Mallat，1999；Mallat，2008)连续小波变换(continue wavelet transform，CWT)缺乏对测井曲线趋势变化的刻画能力，离散小波变换(discrete wavelet transform，DWT)在检测曲线突变点时存在偏移误差，而平稳小波变换(stationary wavelet transform，SWT)结合了CWT和DWT的优点，既具有平移不变性又保证曲线在分解过程中无需下采样处理.基于上述认识，赵淑娥等(2013)将SWT方法应用到南堡凹陷东营组的准层序组划分，并利用理论模型验证该方法的有效性.然而，随着钻孔参数测试技术及多重地层划分理论(柳永清等，1997)的快速发展，需要根据不同的研究目的，综合使用多种相应测井数据对地层进行不同种类的划分.小波变换仅能实现单一测井参数的分层，沃尔什变换(Walsh transform)则突破了这一局限，Maiti和Tiwari(2005)使用沃尔什变换对德国大陆深钻项目钻孔进行岩性单元划分，史清江等(2006)指出沃尔什分层方法的等步长性影响了其分层精度.

以上研究表明，对岩性序列进行地层划分主要基于两点：首先是地层剖面的岩性更迭具明显的旋回特征；其次是奇异点对岩层划分具有指示意义.传统最优分割法不能充分发掘测井曲线所蕴含的信息，且计算效率不高；窗口边缘检测方法可以刻画测点的奇异性，在消除窗宽影响及精确定位方面有改进余地；小波多尺度分析能实现信号分析的时频局部化，但仅能实现单一测井参数的分层；沃尔什变换可以综合使用多种参数，其确定的步长及截止列率性质会影响分层精度.

基于已有的研究成果及存在问题，本文设计了一种边缘最优智能划分算法，可用于多参数测井地层划分.该方法综合最优分割法、小波变换与边缘检测的优点，并引入多种群遗传算法(Multi-Population Genetic Algorithm，MPGA)，兼顾曲线的旋回特征与测点的奇异性，且具有多维、准确、快速的特点.

1 边缘最优智能划分算法原理

1.1 Fisher算法

Fisher算法是传统的有序样品聚类方法，又叫最优分割法.段内离差与总离差的比例S/St称为Fisher比.S与St定义为

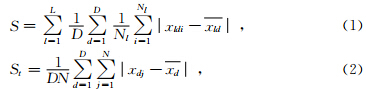
式中：L为分段数，D为参数维数，N为总测点数，Nl为第l段的测点数，xldi为第l段第d种参数第i点的数据，xld 为第l段第d种参数的均值，xdj为第d种参数第j个点数据，xd 为第d种参数的均值.该方法通过最小化Fisher比实现最优划分，Fisher比最小意味着S最小与St最大，也即是每段内都有均匀的物理性质，而段间达到最大差异，故为最优划分.

1.2 LE与WT

由沉积环境突变而引起的旋回变更与沉积间断往往表现在测井曲线的奇异性上，所谓奇异性是指数据序列在某处有间断点或某阶导数不连续.数学上，信号的奇异性用Lipschitz指数(Lipschitz Exponent，LE)来描述，LE在工程领域具有广泛的应用(李春峰和Liner，2005；王佳俊等，2013).对于给定的信号x(t)在t0邻域内满足

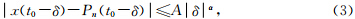
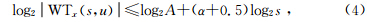
式中：Pn(t)为过x(t0)点的多项式，A是常数，δ是一个充分小的值，则称x(t)在t0处的LE为α.α值越大，光滑度越高；反之，奇异性越大.小波变换可以刻画信号在奇异点的奇异性质，Mallat(1999)建立了WT和LE间的数量关系，为LE的计算提供了理论依据.α值与小波变换的模极大值WTx(s，u)及尺度因子s存在如下关系(Venkatakrishnan et al.， 2012)：

即通过计算小波变换模极大值(Wavelet Transform Modulus Maxima，WTMM)随对数尺度变化曲线的最大斜率来度量LE.

1.3 多种群遗传算法

遗传算法(Genetic Algorithm，GA)是计算机科学人工智能领域中用于解决最优化的一种搜索启发式算法，是进化算法的一种.GA具有高效、并行、全局搜索的特点，普遍应用于机器学习、数学规划、模式识别、自动控制等领域，在定量地层学中也具有广阔的应用前景(肖波等，2010).MPGA是对标准遗传算法(SGA)的一种改进，通过引入移民算子沟通多个不同种群进行协同搜索，克服了SGA早熟及后期收敛较慢的缺点.利用SGA与MPGA进行地层划分的流程如图 1、2所示.

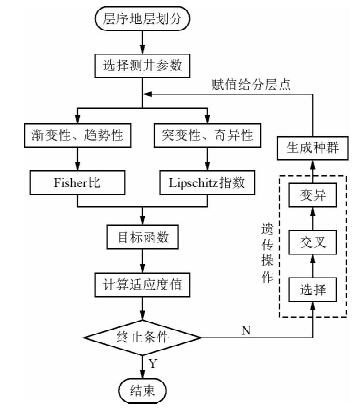图 1 SGA算法分层计算流程图 Fig. 1 Calculation process of SGA algorithm in stratigraphic classification

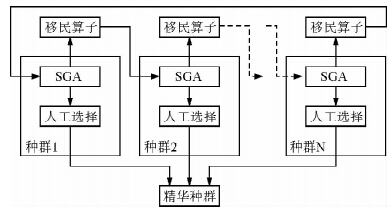图 2 MPGA算法流程图 Fig. 2 Calculation process of MPGA algorithm
1.4 小 结

地层划分需要根据不同的研究目的选择相应的测井参数，并通过碎石图、时(深)频分析或先验知识等确定分层数L，对所选的D种测井数据进行归一化处理可以消除不同量纲之间的差异.根据式1~2计算Fisher比，根据式4计算每种测井参数各奇异点的LE，构造目标函数为

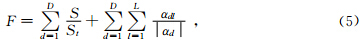
式中：αdl为第d种参数第l个分层点处的LE，αd为第d种参数所有奇异点的LE之和.将初始种群赋值给分层点，按照MPGA的计算流程通过极小化F值寻求最优分层位置.

2 应用实例

2.1 数据来源

HS-2013ZK位于河北省衡水市深州市大屯镇大屯村(E115°22′16.35″，N 37°47′23.25″)，总进尺130 m.根据岩性变化特征，共采集颗分样品135件.2013年10月由中国地质大学(武汉)生物地质与环境地质国家重点实验室采用全自动激光粒度仪(LS230，测限0.04~2000 um)对该样品进行测试.

2.2 LE计算过程

首先计算各指标在多个尺度下的小波变换，然后根据WTMM求出极大曲线序列，记录起始位置与长度，绘制极大曲线在log2s-log2 WTx(s，u) 平面上的曲线图，最后通过求出最大斜率得到LE(图 3).

图 3 HS-2013ZK颗分数据的小波变换(a1黏粒；b1粉粒；c1砂粒)和LE(a2黏粒；b2粉粒；c2砂粒) Fig. 3 Soil fractions data of Borehole HS-2013ZK and its WT and LE(a clay; b silt; c s and )
2.3 MPGA寻优过程

根据对黏粒、粉粒与砂粒进行小波变换得到的时频特征，初步确定分层数为14，并按式(5)构造的目标函数，以参数测点为基因，以有序测点组为染色体，通过MPGA实现多参数层序地层的边缘最优智能划分.测点搜索过程、目标函数、及分层结果对比如图 4所示.

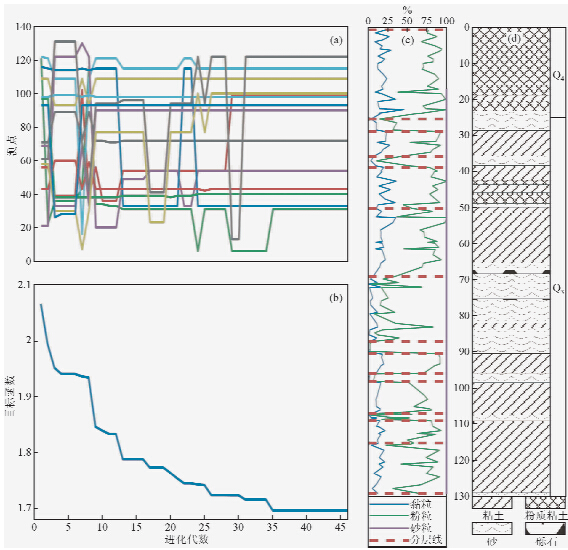图 4 MPGA寻优过程与分层结果对比
(a)测点寻优过程；(b)目标函数；(c)分层结果；(d)野外描述. Fig. 4 Optimization process of MPGA and the division result comparison to the field lithological records
(a)Optimization process of measurement points;(b)Objective function;(c)Division result;(d)Field lithological records.
2.4 地层划分结果对比

测点数据本质上是一个离散的序列，这是由于约1 m的取样间距(135个样品/129.2 m)难以兼顾厚度尺度在几厘米至十几厘米的薄层夹层，导致粒径曲线(图 4c)上会缺失部分薄层数据信息.另外，在野外描述结果中，埋深68与76 m处有薄层砾石夹层(图 4d)，受LS230仪器测限限制，无法进行颗分测试，粒径曲线上缺失砾石夹层的测点数据(图 4c).事实上，可以通过筛分法补全该砾石夹层数据.综上所述，由于取样密度和样品测试技术原因，分层算法计算出的划分结果与野外描述存在细微差异，可以通过增加薄层夹层处的取样密度与测试方法提高测点数据的分辨率.总体而言，使用该边缘最优智能划分算法进行地层划分，所得分层界限皆位于颗分组成发生明显变化的位置，与野外描述相吻合，说明该方法能够充分利用测井参数的形态信息，分层结果符合地质实际.在分层效率方面，本案例设置了10个种群并行搜索最优分层方案，每个种群40个个体，进化36代得到最优解，最优解稳定保持10代终止计算，整个地层划分工作在数秒内完成，计算效率较高，且具有良好的数据与图形输出能力.

3 结 论

3.3     本文提出的边缘最优智能划分算法，将Fisher最优分割、边缘检测LE与MPGA有机集合，能够充分利用测井参数的形态信息，快速有效地实现多维层序地层的自动划分.

3.3    使用的Fisher最优分割原理使得划分后的每段地层都具有均匀的物理性质，WT具有多分辨率分析能力，LE可用于检测由沉积环境的突变而引起的旋回变更与沉积间断点，契合层序地层的旋回与突变特征.

3.3    受地质历史时期多次河流改道的影响，河北平原各种质地的沉积物交错分布，兼具多维、快速、准确的边缘最优智能划分算法能够应用于该地区地层划分与对比工作中.

致 谢 中国地质大学(武汉)在读博士研究生牛宏与刘亚磊两位同学，分别在本文的实验与写作过程中提供了帮助和建议，匿名审稿专家为本文提出了细致而宝贵的修改意见，在此一并表示感谢.

参考文献
[1] Cao X Y, Chang X, Liu Y K, et al. 2009. Singularity properties of well log and their application in high resolution sequence[J]. Chinese Journal of Geophysics (in Chinese), 52(3): 824-832.
[2] Chen T, Wang Z H, Qiang X K, et al. 2013. Magnetic properties of minerals recorded by the borehole WJ and Late Quaternary transgressions in the Taihu plain, southern Yangtze Delta[J]. Chinese Journal of Geophysics (in Chinese), 56(8): 2748-2759, doi: 10.6038/cjg20130823.
[3] Cheng D, Yang Q, Zhang Y B, et al. 2007. Three-dimensional geological modeling based on hydro sections[J]. Journal of Beijing University of Aeronautics and Astronautics (in Chinese), 33(11): 1362-1366.
[4] Li C F, Liner C. 2005. Singularity exponent from wavelet-based multiscale analysis: A new seismic attribute[J]. Chinese Journal of Geophysics (in Chinese), 48(4): 882-888.
[5] Liu B T, Zhou W K, Xia Z Y. 2000. Quantative stratigraphic dividing and correlating by lithological successions[J]. Experimental Petroleum Geology (in Chinese), 22(4): 371-374.
[6] Liu Y Q, Li Y, Liu X W. 1997. Sequence stratigraphic, cyclic stratigraphic and multiple stratigraphic division--A case study of the lower Paleozoic in western Beijing and northern Hebei[J]. Regional Geology of China (in Chinese), 16(1): 82-89.
[7] Maiti S, Tiwari R K. 2005. Automatic detection of lithologic boundaries using the Walsh transform: A case study from the KTB borehole[J]. Computers & Geosciences, 31(8): 949-955.
[8] Mallat S. 1999. A Wavelet Tour of Signal Processing[M]. 2nd ed. London, England: Academic Press.
[9] Mallat S. 2008. A Wavelet Tour of Signal Processing: the Sparse Way[M]. 3rd ed. London, England: Academic Press.
[10] Pan S Y, Hsieh B Z, Lu M T, et al. 2008. Identification of stratigraphic formation interfaces using wavelet and Fourier transforms[J]. Computers & Geosciences, 34(1): 77-92.
[11] Ren J F, Liao Y T, Sun M, et al. 2013. A method for quantitative division of sequence stratigraphy with high-resolution based on wavelet transform and its application[J]. Progress in Geophys. (in Chinese), 28(5): 2651-2658, doi: 10.6038/pg20130546.
[12] Shaaban F F, Ghoneimi A E. 2001. Implication of seismic and borehole data for the structure, petrophysics and oil entrapment of Cretaceous-Palocene reservoirs, northern Sirt Basin, Libya[J]. Journal of African Earth Sciences, 33(1): 103-133.
[13] Shi Q J, Wang Y J, Sun Z Y, et al. 2006. Joint application of wavelet transform and Walsh transform for automatic segmentation of well logs[J]. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese), 30(2): 138-142.
[14] Venkatakrishnan P, Sangeetha S, Sundar M. 2012. Measurement of Lipschitz exponent (LE) using wavelet transform modulus maxima (WTMM)[J]. International Journal of Scientific & Engineering Research, 3(6): 1-4.
[15] Wang J J, Pan L P, Cao S L. 2013. Wavelet transforms applied to cavitation noise analysis for hydro-turbine[J]. Journal of Hydroelectric Engineering (in Chinese), 32(4): 215-220.
[16] Wonik T. 2001. Gamma-ray measurements in the Kirchrode I and II boreholes[J]. Palaeogeography, Palaeoclimatology, Palaeoecology, 174(1-3): 97-105.
[17] Xiao B, Han X H, Zhou K J, et al. 2010. A review and outlook of automatic zonation methods of well log[J]. Progress in Geophys. (in Chinese), 25(5): 1802-1810, doi: 10.3969/j.issn.1004-2903.2010.05.038.
[18] Xu Y, Hao T Y, Dai M G, et al. 2007. Integrated geophysics research on distribution of residual basins of Bohai Sea[J]. Chinese Journal of Geophysics (in Chinese), 50(3): 868-881.
[19] Zhang Z F, Xie Z H, Li B L, et al. 2009. A genetic algorithm for optimal stratigraphic division using multi-parameter log data with application to mesozoic strata in Jiyang depression, Shandong[J]. Earth Science(Journal of China University of Geosciences) (in Chinese), 34(4): 682-690.
[20] Zhao J L, Li N. 2008. Application of wavelet transform to high resolution sequence analysis[J]. Progress in Geophys. (in Chinese), 23(4): 1230-1235.
[21] Zhao S E, Wang H, Liu X L, et al. 2013. A method for quantitative division of sequence stratigraphy with high-resolution using logging data and its application[J]. Journal of Central South University(Science and Technology) (in Chinese), 44(1): 233-240.
[22] 曹向阳, 常旭, 刘伊克,等. 2009. 测井曲线的奇异性特征在高分辨率层序地层学研究中的应用[J]. 地球物理学报, 52(3): 824-832.
[23] 陈艇, 王张华, 强小科,等. 2013. 太湖平原WJ孔矿物磁学特征以及晚第四纪海侵事件[J]. 地球物理学报, 56(8): 2748-2759, doi: 10.6038/cjg20130823.
[24] 程丹, 杨钦, 张永波,等. 2007. 基于水文剖面的三维地质建模方法[J]. 北京航空航天大学学报, 33(11): 1362-1366.
[25] 李春峰, Liner C. 2005. 基于小波多尺度分析的奇性指数: 一种新地震属性[J]. 地球物理学报, 48(4): 882-888.
[26] 刘伯土, 周维奎, 夏遵义. 2000. 岩性序列定量地层划分对比方法[J]. 石油实验地质, 22(4): 371-374.
[27] 柳永清, 李寅, 刘晓文. 1997. 层序地层旋回地层与多重地层划分——以京西冀北下古生界为例[J]. 中国区域地质, 16(1): 82-89.
[28] 任金锋, 廖远涛, 孙鸣,等. 2013. 基于小波变换的高精度层序地层定量划分研究及其应用[J]. 地球物理学进展, 28(5): 2651-2658, doi: 10.6038/pg20130546.
[29] 史清江, 王延江, 孙正义,等. 2006. 小波变换和沃尔什变换在测井曲线分层中的联合应用[J]. 中国石油大学学报(自然科学版), 30(2): 138-142.
[30] 王佳俊, 潘罗平, 曹树良. 2013. 小波变换应用于水轮机空化信号检测[J]. 水力发电学报, 32(4): 215-220.
[31] 肖波, 韩学辉, 周开金,等. 2010. 测井曲线自动分层方法回顾与展望[J]. 地球物理学进展, 25(5): 1802-1810, doi: 10.3969/j.issn.1004-2903.2010.05.038.
[32] 徐亚, 郝天珧, 戴明刚,等. 2007. 渤海残留盆地分布综合地球物理研究[J]. 地球物理学报, 50(3): 868-881.
[33] 张振飞, 谢忠怀, 李宝利,等. 2009. 多参数测井地层划分的遗传最优分割法及其在济阳坳陷中生界中的应用[J]. 地球科学(中国地质大学学报), 34(4): 682-690.
[34] 赵军龙, 李娜. 2008. 小波变换在高分辨率层序地层分析中的应用[J]. 地球物理学进展, 23(4): 1230-1235.
[35] 赵淑娥, 王华, 刘小龙,等. 2013. 基于测井数据的高精度层序地层定量划分方法及其应用[J]. 中南大学学报(自然科学版), 44(1): 233-240.