2. 中国石油大学地球科学与技术学院, 青岛 266580
2. School of Geosciences, China University of Petroleum, Qingdao 266580, China
由于海洋油气藏具有规模大,产量高的特点,近年来随着勘探技术的不断发展,海洋油气勘探受到了越来越多的关注.海水层反射的特殊性对海洋勘探中数据采集以及数据处理带来了很多的难题.其中,海上资料处理中面临的一个很大的困扰就是多次波问题.
在常规的处理过程中,多次波的存在会严重影响地震资料的处理以及后续的解释工作,因而多被视为噪音进行去除;但是考虑到多次波也是来自地下的真实反射,也包含地下的构造信息,近年来,很多学者对多次波的有效利用开展了大量的工作,即对其进行成像处理.
多次波压制一直都是处理多次波问题的首要选择,目前发展的多次波压制方法主要分为两大类.一类是基于一次波和多次波之间的时差差异或者根据多次波的周期性而发展的信号滤波方法.基于一次波和多次波之间剩余时差差异的方法主要有CMP叠加,f-k滤波法、Radon变换、聚束滤波法等(李鹏等,2006).典型的基于多次波周期性的多次波方法是预测反褶积方法.第二类则是基于波动理论的多次波预测相减法,目前发展的该类方法主要有波场外推法,反馈迭代法和逆散射级数法(李鹏等,2006).滤波法具有高效的计算效率,但是在一次波和多次波剩余时差差距不大或者地下较为复杂的情况下,该类方法较难获得理想的多次波压制效果,而基于波动理论的预测相减法则考虑了复杂的波场传播,能较好的处理复杂地下情况,但是却是以高计算成本为代价的.为了兼顾多次波压制的精度和计算成本,很多学者对两种方法结合来压制多次波的方法开展了大量研究,并取得了一定的成果.
长期以来,多次波都被视为噪音,在地震资料处理过程中要对其进行压制,但是,考虑到多次波也是来自地下的真实反射,如果能有效利用,相比一次波,多次波传播路径的特殊性,尤其是海上多次波,将会获得更广的地下照明和更为丰富的地下信息.近年来,越来越多的学者开始考虑将多次波信息进行有效利用,对多次波成像方法开展了大量的研究.
文中首先对海上多次波的产生机理、分类及识别进行简要的分析,然后对国内外目前发展的海上多次波压制与成像的方法进行了详细的总结,并对多次波问题的发展趋势进行了展望.
1 海上多次波特征分析
多次波的产生需要反射界面上下介质的波阻抗差异较大,即存在良好的反射界面.海洋地震勘探中,由于海水与空气界面以及海水与海底界面是两个强反射界面,其中,海水与空气界面反射系数接近-1,波到达该界面时,反射能量大,又由于海水对声波衰减作用较小,这样地震波在海水中传播时,就会形成来回于海面、海水以及海底之间的多次反射,于是在采集到的海上地震记录中往往会包含能量较强的多次反射波.
由于海洋勘探的特殊性,多次波种类也较多.海洋地震勘探中常见的多次波类型按照多次波传播路径可以分为:全程多次波、短程多次波、微曲多次波、虚反射等(陆基孟和王永刚,2001;刘建辉,2010),其传播路径见图 1所示.
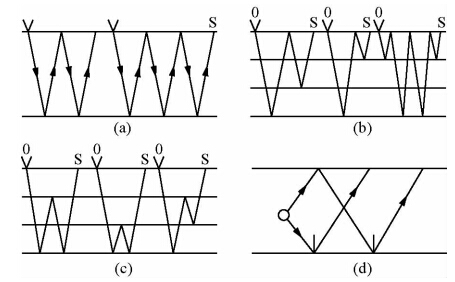 | 图 1(a)全程多次波;(b)短程多次波;(c)微屈多次波;(d)虚反射(刘建辉,2010) Fig. 1(a)Long path multiple;(b)Shot path multiple;(c)Peg-leg multiple;(d)Ghost reflection(Liu,2010) |
而根据多次波产生的界面不同,海上多次波又可以分为海上表层多次波(surface-related multiple)和层间多次波(internal multiple)(陆基孟和王永刚,2001;刘建辉,2010).由于海水表面近似自由表面,在海洋勘探采集资料中往往发育有大量的表层多次波,严重困扰采集数据的处理.而在海底以下存在的强反射层则经常会产生较强的层间多次波.图 2中给出了海上地震勘探中表层多次波和层间多次波类型的路径示意图.
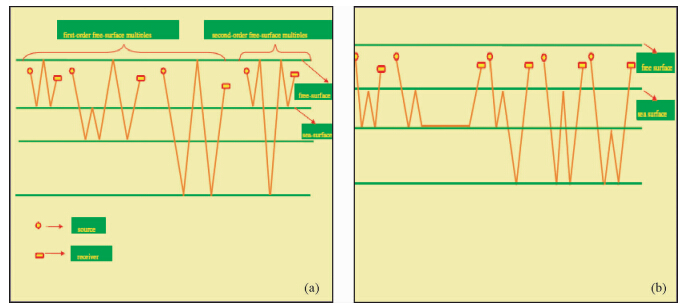 | 图 2(a)海上表层多次波,(b)海上层间多次波(Watts,2005) Fig. 2(a)offshore surface-related multiples,(b)offshore internal multiple(Watts,2005) |
为了有效处理海洋地震勘探中的各种多次波,必须要先对多次波的存在进行合理的判断.判定多次波存在的主要依据为:
(1)利用反射波的t0标志和倾角标志识别多次波.反射界面倾角较小情况下,一阶多次波出现时间约为同一界面一次波时间的两倍.而存在倾斜地层时,叠前剖面上一阶多次波倾角约为一次波倾角的两倍.
(2)利用合成地震记录识别多次波,通过人工合成包含多次波的地震记录来对多次波进行识别.
(3)利用速度谱识别多次波.当对含有多次波的地震资料进行速度分析时,多次波的速度随着时间的增加是减小的或者基本保持不变的,而一次波速度则是随深度增加而增加,通过这一特征可以识别多次波.
(4)利用多种地球物理资料综合识别多次波.对一个区域进行地震资料的正确解释,往往需要对物探、测井以及钻井资料进行综合研究来完成,因此结合除地震勘探资料外的其他资料来对多次波进行识别也是很重要的一种手段(刘建辉,2010).
2 多次波压制方法
2.1 滤波法多次波压制方法
早在20世纪60年代,Bortfeld(1961)就提出基于正常时差和周期性来识别多次波.之后,诸多专家基于多次波与一次波的时差差异和海上多次波的周期性发展了多种基于滤波理论的多次波压制方法.
常用的基于正常时差进行多次波压制的方法可总结概述如下:
1)CMP叠加.Yilmaz(1987)最先为该方法的实现奠定了理论基础,Schneider和Backus(1968)、Taner和Koehler(1969)研究了利用CMP零偏移距消除多次波的方法.该方法依据多次波和一次波存在速度差异,在NMO后一次波拉平,多次波动校正量不足而呈现为弯曲的同相轴,利用一次波速度进行CMP叠加就可以实现一次波的同相叠加和多次波的非同相叠加,从而压制掉一部分多次波,该方法在近偏移距处多次波压制效果很差.
2)f-k滤波法.Ryu(1982)基于f-k视速度滤波法来进行多次波压制,NMO后的CMP记录中一次波和多次波呈现不同的形态,对其进行二维傅里叶变换,在f-k域内多次波和一次波将分布在不同的象限内,根据这一原理实现对多次波的压制,该方法也不能很好的处理近偏移距多次波,且在进行多次波去除的过程中容易损伤有效波,此外,一次波或者多次波的空间假频问题可能会使得多次波压制后的数据中残留多次波分量.
3)Radon变换.基于多次波和一次波正速度梯度差异在Radon域内具有可分离性,Thorson和Claerbout(1985)提出了速度叠加变换和倾斜叠加变换技术,利用在τ-p域内一次波表现为一个点,而多次波则表现为一段椭圆弧,根据这一特性来压制多次波.Hampson(1986)对倾斜叠加进行改进,提出了用抛物Radon变换压制多次波的方法,该方法利用在抛物Radon域内一次波和多次波分别聚焦在不同位置的点上这一特性来实现多次波压制.Foster和Mosher(1992)在抛物Radon变换的基础上发展了双曲Radon变换压制多次波的方法,采用双曲Radon变换在Radon域一次波和多次波聚焦点具有更好的收敛性,但是同时也增加了方法实现的难度.国内外很多专家对Radon变换压制多次波开展了大量的研究.其中,国外的Yilmaz(1989)、Sacchi和Ulrych(1995)、Sacchi和Porsani(1999)、Cary(1998)、Trad 等(2003)、Schonewille和Aaron(2007)等以及国内的顾建平(2003)、熊登等(2009)、薛亚茹等(2012)等学者都对Radon变换多次波压制算法的改进做出了巨大的贡献.
4)聚束滤波法.聚束滤波在输出噪音能量最小的约束前提下可提取无畸变的信号,它是一种多道滤波方法.胡天跃等(2000,2002)对聚束滤波法压制多次波技术给出了详细的理论推导并进行了资料试算.聚束滤波方法在避免畸变方面有一定的优势,但是对数据信噪比还有动校正变化量都比较敏感.
而基于周期性的多次波压制方法主要为预测反褶积以及在此基础上发展的改进算法.Robinso和Backus利用多次波的周期性分别引入了维纳滤波和预测反褶积来进行多次波的压制.采用预测反褶积进行多次波压制效率较高,但是存在明显的缺陷,如预测步长较难确定,难以准确预测多次波,对长周期多次波衰减效果差等问题.Taner(1980)认为沿径向道方向多次波周期性更强,将线性Radon变换与预测反褶积相结合实现了长周期多次波的压制.
2.2 预测相减法多次波压制方法
目前发展的基于波动理论的预测相减法主要有:波场外推法,反馈迭代法,逆散射级数法等.
1)波场外推法.该方法是基于模型驱动的,通过波场延拓模拟多次波在水中的传播,并通过自适应滤波法对预测的多次波进行去除.该方法存在很多局限性,如需要知道海水深度先验信息,对震源子波和海底反射系数信息依赖性强等.Riley和Claerbout(1976)等人对一维多次波资料进行了试处理,并进行了更为详细的方法推导及实现.Wiggins(1988)对该方法进行了进一步完善.
2)反馈迭代法(SRME).该方法与波场外推法不同,是基于数据驱动的,主要用于压制表层多次波.Berkhout和Verschuur(1997)、Verschuur和Berkhout(1997)提出了“反馈环”的概念,对自由表面多次波衰减方法理论进行了总结.van Dedem和Verschuur(2002)将该方法扩展到了三维地震资料处理中.石颖等(2010,2013)对该方法的GPU实现以及三维实现进行了深入研究.马继涛等(2011)对该方法进行改进,将其用于海底电缆数据中.谢宋雷等(2013)对该方法进行改进并将其用于深水陡坡带绕射多次波的压制.该方法采用迭代形式进行多次波衰减,计算成本较高,同时该方法要求数据规则化.
在采用该方法进行多次波预测以后往往需要通过最小能量准则来进行多次波匹配相减,但是基于这种准则的方法并不是最佳的(Nekut and Verschuur, 1998; Guitton and Verschuur, 2004; van Groenestijn and Verschuur, 2008),因而,van Groenestijn和Verschuur(2009a)在SRME基础上提出基于稀疏反演的一次波估计方法(EPSI),该方法将SRME的预测和相减通过全波形反演来实现.Lin和Herrmann(2009,2010)在曲波域对EPSI进行了重新定义.刘国昌等(2013)对该方法在海底拖缆数据的实现开展了进一步工作.
3)逆散射级数法. 该方法根据逆散射理论,基于自由界面和点散射模型,通过多维直接反演,利用散射序列中的某些高阶项来预测并压制多次波.Carvalho(1992)最先提出这一理论,Weglein 等(1997)对该方法进行了详细推导.同反馈迭代法一样,该方法实现不需要任何地下信息,但是需要数据规则化,该方法相比反馈迭代法可以有效保存一次波能量,且不需要迭代运算,在地下构造复杂时该方法具有更明显的优势.Malcolm(2004)对Weglein方法进行了改进,使其有更广的适用范围.
预测相减多次波压制方法实现分为两个过程,一是多次波的预测,二是多次波的减去.在多次波压制过程中往往存在较多问题的不是预测而是相减,在一次波和多次波同相轴非正交时,采用能量最小准则进行匹配相减效果往往不是很理想.Monk(1993)提出伪多道匹配的方法,该方法相比最小二乘有一定的改善,但是还是会存在一次波的损伤.Wang(2003)在伪多道匹配基础上引入空间多道均衡发展了均衡伪多道算法,压制效果得到了一定改善.李振春等(2011)提出基于扩展伪多道匹配的保幅型多次波压制方法,通过对扩展伪多道匹配方法进行改进,该方法可以同时实现较好的多次波压制效果和一次波能量的有效保存.此外,陆文凯等(2004)提出利用独立分量分析技术基于输出信号非高斯性最大准则来进行多次波的自适应相减.李学聪等(2010)提出基于1范数最小的均衡多道自适应匹配滤波法来进行多次波的匹配相减.董烈乾等(2013)采用非因果匹配滤波器来进行多次波的匹配相减.
2.3 滤波理论和波动理论相结合多次波压制方法
前面两节中对基于滤波理论和基于波动理论的多次波压制方法进行了概述,各种方法都有其所长,但是同时也存在一定的缺陷.基于滤波理论的多次波压制方法计算效率高,但是多次波压制精度较低,而基于波动理论的预测相减法则能得到较好的多次波压制结果,但是计算成本巨大.为了能有效兼顾多次波压制的精度和计算效率,很多学者对两种方法结合开展了大量研究.Zhou和Stewart(1996)提出抛物Radon变换和波动方程预测相结合压制多次波的方法,但是其方法实现需要已知表层的深度和速度信息以及海底的起伏情况,所以在应用中受到了一定的限制.Sava和Fomel(2003)等对成像域衰减多次波的方法进行了研究,首先基于波动理论进行偏移得到局部偏移道集,根据一次波和多次波在道集中呈现的不同特征,利用滤波方法进行多次波的压制,取得了较好的多次波压制效果.王维红等(2007)对将波动理论预测和抛物Radon变换相结合压制多次波的方法进行了深入研究.石颖和王维红(2012)则提出将波动方程预测和双曲Radon变换联合压制表层多次波的方法.赵昌垒等(2013)通过将SRME方法与线性Radon域预测反褶积以及高精度Radon滤波相结合对深海资料进行多次波压制,根据SRME能有效衰减表层多次波,线性Radon域预测反褶积可以消除长周期多次波,而高精度Radon滤波对远偏移距多次波能进行有效的去除,结合这些优势对海上资料进行多次波压制效果显著.
目前发展的滤波理论和波动理论多次波压制方法都存在一定的限制条件,这极大的影响了方法的应用范围及数据处理的精度.滤波理论和波动理论方法相结合已成为多次波压制技术发展的一个趋势.李振春,李志娜等(2013)等对采用滤波理论和波动理论以及结合两种理论的成像域多次波压制方法压制多次波的效果进行了对比,图 3为对凹陷模型分别采用抛物Radon变换、反馈迭代法以及成像域多次波压制方法进行多次波压制的效果对比图.通过对比可见,采用滤波理论得到的结果在偏移剖面上存在大量残留的多次波,而基于波动理论的反馈迭代法和成像域多次波压制方法多次波压制效果则较为理想,但是成像域多次波压制方法相比反馈迭代法则极大的降低了计算成本,由此可见结合滤波理论和波动理论进行多次波压制具有更为明显的优势.
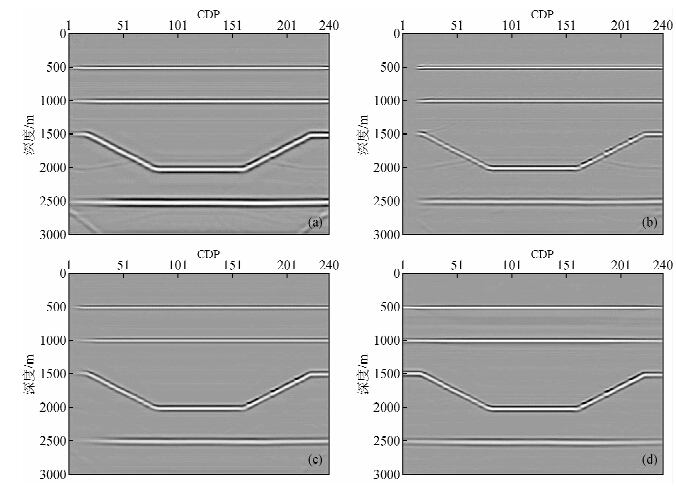 |
图 3 凹陷模型不同方法多次波压制效果对比图(李振春等,2013) (a)原始含多次波炮记录的偏移结果;(b)抛物拉东变换多次波压制结果;(c)SRME+均衡扩展匹配拟多道多次波压制结果;(d)成像域多次波压制结果. Fig. 3 Comparison of multiple attenuation result by different methods(Li et al,2013) (a)migration result of the original shot record with multiples;(b)Multiple attenuation result by Parabolic Radon transform;(c)Multiple attenuation result by SRME and equipoise exp and ed pseudomulti-channel matching and subtracting;(d)Multiple attenuation result in image domain. |
目前,多次波压制技术在国内外已经取得了飞速的发展,基于滤波理论的多次波压制方法因其成本较低在生产中得到了广泛的应用.但是随着计算机技术的不断发展,基于波动理论的SRME以及逆散射级数法得到了飞速的发展,近几年SEG年会中对于SRME以及逆散射级数法的改进算法研究不断涌现,其中,3DSRME受到了很多的关注,基于SRME改进的反演算法EPSI也在近几年成为一个研究热点.而基于滤波理论和波动理论的多次波压制方法因其能综合考虑多次波压制的精度和计算效率在近年来也受到了越来越多地球物理工作者的青睐.
3 多次波成像方法
考虑到多次波也是来自地下的真实反射,跟一次波一样,也包含着地下界面的信息,尤其是在地下复杂情况下,多次波往往会具有比一次波更广的照明范围,包含比一次波更为丰富的地下信息,利用多次波信息可以改善一次波成像的效果.图 4中由Sigsbee2b模型一次波震源照明与一次波和多次波联合成像时震源照明范围的对比可看出在多次波辅助下可以获得比一次波成像更广的照明范围.因而,近年来,很多地球物理学家对多次波的有效利用开展了大量研究.目前发展的多次波成像方法大致可以分为两类:
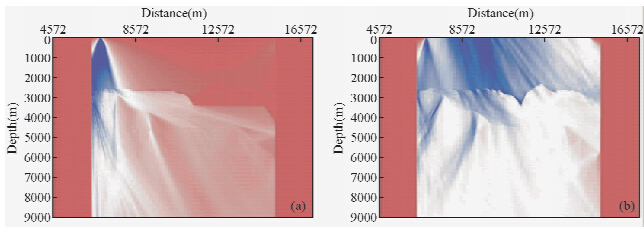 |
图 4 基于Sigsbee2B模型数据利用单炮记录进行偏移的震源照明 (a)常规单炮一次波偏移时的震源照明情况;(b)一次波和多次波联合成像时震源照明(郭书娟,2012) Fig. 4 Source power spectra created from one shot of Sigsbee2B datasets on top of the model’s reflectivity (a)From a pulse source for imaing of primary;(b)from the complex downgoing wavefields including pulse source and the sum of primaries and multiples for joint imaging(GUO,2012) |
1)对多次波单独成像
Reiter等(1991)首先提出利用叠前Kirchhoff方法对深水多次波进行成像.Berkhout和Verschuur(1994)、Guitton(2002)采用先提取多次波,然后用一次波和多次波记录代替震源子波,用多次波作为接收记录,采用常规成像方法对多次波进行成像.Liu 等(2011)结合逆时偏移,采用互相关成像条件采用同样的方法对多次波进行成像.Berkhout和Verschuur(2006)、Verschuur和Berkhout(2005)基于聚焦变换的理论,通过多道加权互相关和SRME中的加权褶积联合处理,实现多次波向一次波的转换并实现多次波成像;Shan(2003)、郭书娟等(2012)等基于互相关将多次波转换为准一次波,再利用一次波成像方法对准一次波进行成像,该方法构建的准一次波和一次波形态相似,可用于补充由于常规观测系统的限制造成的远或近炮检距数据的缺失.
2)一次波和多次波联合成像
也有很多学者尝试将多次波和一次波同时进行偏移成像.He和Schuster(2003)、Brown和Guitton(2005)等人采用最小二乘联合成像方法同时对一次波和多次波进行成像.郭书娟等(2011)基于广义的炮偏移方法来实现表层多次波和一次波的联合成像,该方法基于单程波动方程偏移的思路,将脉冲震源与原始包含一次波和多次波记录之和作为向下正向延拓的震源波场,将同时含有一次波和多次波的记录作为向下逆向延拓的接收波场,并结合2D反褶积成像条件,实现了一次波和表层多次波的联合成像.Berkhout和Verschuur(2011)提出全波场偏移方法,实现了一次波和多次波的同时成像.
从压制到成像,多次波的有效利用为地下构造成像注入了新鲜血液.在2013年的SEG年会多次波主题中特别设立了“From attenuation to imaging”这一专题,由此可以看出多次波的有效利用已得到国内外专家的普遍认可,目前该类方法大都处于理论研究中,这将是多次波处理的一个重要的发展趋势.
4 结 论
本文中通过海上多次波特征分析,对海上多次波产生机制及分类等有了深入的了解.然后基于国内外大量文献调研,对目前多次波的两种处理方式——多次波压制和多次波成像技术进行了总结概括.常用的基于滤波理论和基于波动理论的两类多次波压制方法在实际应用中面临着计算效率和计算精度的权衡问题,而将两种方法相结合进行多次波压制可以有效兼顾多次波压制的精度和计算效率,这也成为目前多次波压制的一种趋势.而考虑到多次波也包含丰富的地下信息,很多学者对多次波成像方法进行了深入研究,并取得了一定的成果.多次波往往包含比一次波更多的地下信息,这为地震勘探带来了福音,但是多次波成像处理还处于起步阶段,目前在实现过程中还面临着一些问题,如在对多次波进行成像时,多阶多次波以及层间多次波的存在会导致成像中大量噪音的产生,因而对多次波成像方法的研究还有待进一步完善.
致 谢 衷心感谢审稿专家对本文提出的宝贵意见和编辑部老师的付出.
| [1] | Backus M M. 1959. Water reverberations; their nature and elimination[J]. Geophysics, 24(2): 233-261. |
| [2] | Berkhout A J, Verschuur D J. 1994. Multiple technology: Part 2, migration of multiple reflections[C].//64th Annual International Meeting, SEG, Expanded Abstracts, 1497-1500. |
| [3] | Berkhout A J, Verschuur D J. 1997. Estimation of multiple scattering by iterative inversion, Part I: Theoretical considerations[J]. Geophysics, 62(5): 1586-1595. |
| [4] | Berkhout A J, Verschuur D J. 2006. Imaging of multiple reflections[J]. Geophysics, 71(4): S1209-S1220. |
| [5] | Berkhout A J, Verschuur D J. 2011. Full wavefield migration, utilizing surface and internal multiple scattering[C].//81th Annual International Meeting, SEG, Expanded Abstracts, 3212-3216. |
| [6] | Bortfeld R. 1961. Multiple Reflexionen in Nordwestdeutschland[J]. Geophysical Prospecting, 4(4): 394-423. |
| [7] | Brown M P, Guitton A. 2005. Least-squares joint imaging of multiples and Primaries[J]. Geophysics, 70(5): S79-S89. |
| [8] | Carvalho F M, Weglein A B, Stolt R H. 1991. Examples of a nonlinear inversion method based on the t matrix of scattering theory: application to multiple suppression[C].//79th Annual International Meeting, SEG, Expanded Abstracts, 1319-1322. |
| [9] | Cary P W. 1998. The simplest discrete Radon transform[C].//68thAnnual International Meeting, SEG, Expanded Abstracts, 1999-2002. |
| [10] | Dong L Q, Li Z C, Yang S C, et al. 2013. Non-causal matching filter multiple elimination method based on correlation and iteration[J]. Chinese J. Geophys. (in Chinese), 56(10): 3542-3551, doi: 10.6038/cjg20131029. |
| [11] | Foster D J, Mosher C C. 1992. Suppression of multiple reflections using the Radon transform[J]. Geophysics, 57(3): 386-395. |
| [12] | Gu J P. 2003. Improved Radon filter multiple attenuation technology and its application effect[J]. OGP (in Chinese), 38(S): 38-41. |
| [13] | Guitton A. 2002. Shot-profile migration of multiple reflections[C].//72th Annual International Meeting, SEG, Expanded Abstracts, 1296-1299. |
| [14] | Guitton A, Verschuur D J. 2004. Adaptive subtraction of multiples using the l1-norm[J]. Geophysical Prospecting, 52(1): 27-38. |
| [15] | Guo S J, Li Z C, Tong Z Q, et al. 2011. Joint imaging of primaries and surface-related multiples based on generalized shot-profile migration[J]. Chinese J. Geophys. (in Chinese), 54(4): 1098-1105, doi: 10.3969/j.issn.0001-5733.2011.04.025. |
| [16] | Guo S J, Li Z C, Tong Z Q, et al. 2012. Method and technique for imaging of surface-related multiples[J]. Progress in Geophys. (in Chinese), 27(6): 2570-2576, doi: 10.6038/j.issn.1004-2903.2012.06.034. |
| [17] | Guo S J. 2012. Seismic imaging of surface-related multiples (in Chinese)[D]. Shandong: China University of Petroleum (Huadong). |
| [18] | Hampson D. 1986. Inverse velocity stacking for multiple elimination[C].//56th Annual International Meeting, SEG, Expanded Abstracts, 422-424. |
| [19] | He R, Schuster G. 2003. Least-squares migration of both primaries and multiples[C].//73th Annual International Meeting, SEG, Expanded Abstracts, 1035-1038. |
| [20] | Hu T Y, Wang R Q, White R E. 2000. Beamforming in seismic data processing[J]. Chinese J. Geophys. (in Chinese), 43(1): 105-115. |
| [21] | Hu T Y, Wang R Q, Wen S L. 2002. Multiple attenuation of seismic data from South China Sea by using beam-forming filtering method[J]. OGP (in Chinese), 37(1): 18-23. |
| [22] | Li P, Liu Y, Chang X, et al. 2006. Progress on the multiple problems[J]. Progress in Geophysics (in Chinese), 21(3): 888-897, doi: 10.3969/j.issn.1004-2903.2006.03.029. |
| [23] | Li X C, Liu Y K, Chang X, et al. 2010. The adaptive subtraction of multiple using the equipoise multichannel L1-norm matching[J]. Chinese J. Geophys. (in Chinese), 53(4): 963-973, doi: 10.3969/j.issn.0001-5733.2010.04.021. |
| [24] | Li Z C, Liu J H, Guo C B, et al. 2011. Amplitude-preserved multiple suppression based on expanded pseudo-multi-channel matching[J]. OGP (in Chinese), 46(2): 207-210. |
| [25] | Li Z C, Li Z N, Guo S J, et al. 2013. Comparison of multiple attenuation methodsin data domain and image domain[J]. Progress in Geophys. (in Chinese), 28(6): 2901-2910, doi: 10.6038/pg20130610. |
| [26] | Lin T T Y, Herrmann F J. 2009. Unified compressive sensing framework for simultaneous acquisition with primary estimation[C].//79th Annual International Meeting, SEG, Expanded Abstracts, 3113-3117. |
| [27] | Lin T T Y, Herrmann F J. 2010. Sparsity-promoting migration from surface-related multiples[C].//80th Annual International Meeting, SEG, Expanded Abstracts, 3333-3337. |
| [28] | Liu G C, Chen X H, Song J W. 2013. Estimation of primaries and multiples by sparse inversion for OBS data with integration of streamer data[J]. Chinese J. Geophys. (in Chinese), 56(12): 4288-4296, doi: 10.6038/cjg20131231. |
| [29] | Liu J H. 2010. Research of multiple suppression method based on wave theory (in Chinese)[D]. Shandong: China University of Petroleum (Huadong). |
| [30] | Liu Y K, Chang X, Jin D G, et al. 2011. Reverse time migration of multiples for subsalt imaging[J]. Geophysics, 76(5): WB209-WB216. |
| [31] | Lu J M, Wang Y G. 2001. The Principle of Seismic Exploration (in Chinese)[M]. Dongying: Petroleum University Press. |
| [32] | Lu W K, Luo Y, Zhao B, et al. 2004. Adaptive multiple wave subtraction using independent component analysis[J]. Chinese J. Geophys. (in Chinese), 47(5): 886-891. |
| [33] | Ma J T, M S K, Chen X H, et al. 2011. OBC multiple attenuation technique using SRME theory[J]. Chinese J. Geophys. (in Chinese), 54(11): 2960-2966, doi: 10.3969/j.issn.0001-5733.2011.11.026. |
| [34] | Malcolm A E. 2004. Inverse multiple scattering in the downward-continuation approach[C].//74st Annual International Meeting, SEG, Expanded Abstracts, 1293-1296. |
| [35] | Monk D J. 1993. Wave-equation multiple suppression using constrained gross-equalization[J]. Geophysical Prospecting, 41(6): 725-736. |
| [36] | Nekut A G, Verschuur D J. 1998. Minimum energy adaptive subtraction in surface-related multiple attenuation[C].//68th Annual International Meeting, SEG, Expanded Abstracts, 1507-1510. |
| [37] | Reiter E C. Toksoz M N, Keho T H, et al. 1991. Imaging with deep-water multiples[J]. Geophysics, 56(7): 1081-1086. |
| [38] | Riley D C, Claerbout J F. 1976. 2-D multiple reflections[J]. Geophysics, 41(4): 592-620. |
| [39] | Robinson E A. 1957. Predictive decomposition of seismic traces[J]. Geophysics, 22(4): 767-778. |
| [40] | Ryu J V. 1982. Decomposition (DECOM) approach applied to wave field analysis with seismic reflection records[J]. Geophysics, 47(6): 869-883. |
| [41] | Sacchi M D, Ulrych T J. 1995. High-resolution velocity gathers and offset space reconstruction[J]. Geophysics, 60(4), 1169-1177. |
| [42] | Sacchi M D, Porsani M. 1999. Fast high resolution parabolic Radon transform[C].//69th Annual International Meeting, SEG, Expanded Abstracts, 1477-1480. |
| [43] | Sava P C, Fomel S. 2003. Angle-domain common-image gathers by wavefield continuation methods[J]. Geophysics, 68(3): 1065-1074. |
| [44] | Schneider W A, Backus M M. 1968. Dynamic correlation analysis[J]. Geophysics, 33(1): 105-126. |
| [45] | Schonewille M A, Aaron P A. 2007. Applications of time-domain high-resolution Radon demultiple[C].//77th Annual International Meeting, SEG, Expanded Abstracts, 2565-2569. |
| [46] | Shan G J. 2003. Source-receiver migration of multiple reflections[C].//73nd Annual International Meeting, SEG, Expanded Abstracts, 1008-1011. |
| [47] | Shi Y, Liu H, Zou Z. 2010. Surface-related multiples prediction based on wave equation and adaptive subtraction investigation[J]. Chinese J. Geophys. (in Chinese), 53(7): 1716-1724, doi: 10.3969/j.issn.0001-5733.2010.07.023. |
| [48] | Shi Y, Wang W H. 2012. Surface-related multiple suppression approach by combining wave equation prediction and hyperbolic Radon transform[J]. Chinese J. Geophys. (in Chinese), 55(9): 3115-3125, doi: 10.6038/j.issn.0001-5733.2012.09.029. |
| [49] | Shi Y, Wang W H, Li Y, et al. 2013. 3D surface-related multiple prediction approach investigation based on wave equation[J]. Chinese J. Geophys. (in Chinese), 56(6): 2023-2032, doi: 10.6038/cjg20130623. |
| [50] | Taner M T, Koehler F. 1969. Velocity spectra-digital computer derivation applications of velocity functions[J]. Geophysics, 34(6): 859-881. |
| [51] | Taner M T. 1980. Long-period sea-floor multiples and their suppression[J]. Geophysical Prospecting, 28(1): 30-48. |
| [52] | Thorson J R, Claerbout J F. 1985. Velocity-stack and slant-stack stochastic inversion[J]. Geophysics, 50(12): 2727-2741. |
| [53] | Trad D, Ulrych T, Sacchi M. 2003. Latest views of the sparse Radon transform[J]. Geophysics, 68(1): 386-399. |
| [54] | van Dedem E J, Verschuur D J. 2002. 3D surface-related multiple prediction: A sparse inversion approach[J]. Geophysics, 70(3): 31-43. |
| [55] | van Groenestijn G J A, Verschuur D J. 2008. Towards a new approach for primary estimation[C].//78th Annual International Meeting, SEG, Expanded Abstracts, 2487-2491. |
| [56] | van Groenestijn G J A, Verschuur D J. 2009a. Estimating primaries by sparse inversion and application to near-offset data reconstruction[J]. Geophysics, 74(3): A23-A28. |
| [57] | Verschuur D J, Berkhout A J. 1997. Estimation of multiple scattering by iterative inversion, Part II: Practical aspects and examples[J]. Geophysics, 62(5): 1596-1611. |
| [58] | Verschuur D J, Berkhout A J. 2005. Transforming multiples into primaries: experience with field data[C].//75th Annual International Meeting, SEG, Expanded Abstracts, 2103-2106. |
| [59] | Wang W H, Cui B W, Liu H. 2007. Research progress in surface-related multiple attenuation[J]. Progress in Geophysics (in Chinese), 22(1): 156-164, doi: 10.3969/j.issn.1004-2903.2007.01.022. |
| [60] | Wang Y H. 2003. Multiple subtraction using an expanded multichannel matching filter[J]. Geophysics, 68(1): 346-354. |
| [61] | Weglein A B, Gasparotto F A, Carvalho P M, et al. 1997. An inverse-scattering series method for attenuating multiples in seismic reflection data[J]. Geophysics, 62(6): 1975-1989. |
| [62] | Wiggins J W. 1988. Attenuation of complex water-bottom multiples by wave-equation-based predication and subtraction[J]. Geophysics, 53(12): 1527-1539. |
| [63] | Xie S L, Liu Y K, Wang Y B, et al. 2013. Study of diffracted multiple elimination on steep slope zone in deep water[J]. Chinese J. Geophys. (in Chinese), 56(9): 3118-3123, doi: 10.6038/cjg20130924. |
| [64] | Xiong D, Zhao W, Zhang J F. 2009. Hybrid-domain high-resolution parabolic Radon transform and its application to demultiple[J]. Chinese J. Geophys. (in Chinese), 52(4): 1068-1077. |
| [65] | Xue Y R, Chen X H, Ma J T. 2012. Multiples attenuation based on directional orthogonal polynomial transform[J]. Chinese J. Geophys. (in Chinese), 55(10): 2450-3458, doi: 10.6038/j.issn.0001-5733.2012.10.028. |
| [66] | Yilmaz . 1989. Velocity-stack processing[J]. Geophysical Prospecting, 37(4): 357-382. |
| [67] | Yilmaz O. 1987. Seismic data processing[R]. Society of Exploration Geophysics. |
| [68] | Zhao C L, Ye Y L, Yao G S, et al. 2013. Prediction deconvolution in linear radon domain on the application of ocean multiples attenuation[J]. Progress in Geophys. (in chinese), 28(2): 1026-1032, doi: 10.6038/pg20130256. |
| [69] | Zhou B Z, Stewart G. 1996. Multiple suppression by 2D filtering in the parabolic τ–p domain: a wave-equation-based method[J]. Geophysical Prospecting, 44(3): 375-401. |
| [70] | 董烈乾, 李振春, 杨少春,等. 2013. 基于相关迭代的非因果匹配滤波器多次波压制方法[J]. 地球物理学报, 56(10): 3542-3551, doi: 10.6038/cjg20131029. |
| [71] | 顾建平. 2003. 改进的Radon滤波压制多次波技术及应用效果[J]. 石油地球物理勘探, 38(增刊): 38-41. |
| [72] | 郭书娟, 李振春, 仝兆岐,等. 2011. 基于广义的炮偏移方法实现地表多次波和一次波联合成像[J]. 地球物理学报, 54(4): 1098-1105, doi: 10.3969/j.issn.0001-5733.2011.04.025. |
| [73] | 郭书娟, 李振春, 仝兆岐,等. 2012. 表层多次波成像方法技术研究[J]. 地球物理学进展, 27(6): 2570-2576, doi: 10.6038/j.issn.1004-2903.2012.06.034. |
| [74] | 郭书娟. 2012. 表层多次波成像方法研究[D]. 山东: 中国石油大学(华东). |
| [75] | 胡天跃, 王润秋, White R E. 2000. 地震资料处理中的聚束滤波方法[J]. 地球物理学报, 43(1): 105-115. |
| [76] | 胡天跃, 王润秋, 温书亮. 2002. 聚束滤波法消除海上地震资料的多次波[J]. 石油地球物理勘探, 37(1): 18-23. |
| [77] | 李鹏, 刘伊克, 常旭,等. 2006. 多次波问题的研究进展[J]. 地球物理学进展, 21(3): 888-897, doi: 10.3969/j.issn.1004-2903.2006.03.029. |
| [78] | 李学聪, 刘伊克, 常旭,等. 2010. 均衡多道1范数匹配多次波衰减的方法与应用研究[J]. 地球物理学报, 53(4): 963-973, doi: 10.3969/j.issn.0001-5733.2010.04.021. |
| [79] | 李振春, 刘建辉, 郭朝斌,等. 2011. 基于扩展伪多道匹配的保幅型多次波压制方法[J]. 石油地球物理勘探, 46(2): 207-210. |
| [80] | 李振春, 李志娜, 郭书娟,等. 2013. 数据域与成像域多次波压制方法对比[J]. 地球物理学进展, 28(6): 2901-2910, doi: 10.6038/pg20130610. |
| [81] | 刘国昌, 陈小宏, 宋家文. 2013. 基于稀疏反演的OBS数据多次波压制方法[J]. 地球物理学报, 56(12): 4288-4296, doi: 10.6038/cjg20131231. |
| [82] | 刘建辉. 2010. 基于波动理论压制多次波方法研究[D]. 山东: 中国石油大学(华东). |
| [83] | 陆基孟, 王永刚. 2001. 地震勘探原理[M].东营: 石油大学出版社. |
| [84] | 陆文凯, 骆毅, 赵波,等. 2004. 基于独立分量分析的多次波自适应相减技术[J]. 地球物理学报, 47(5): 886-891. |
| [85] | 马继涛, Mrinal S K, 陈小宏,等. 2011. 海底电缆多次波压制方法研究[J]. 地球物理学报, 54(11): 2960-2966, doi: 10.3969/j.issn.0001-5733.2011.11.026. |
| [86] | 石颖, 刘洪, 邹振. 2010. 基于波动方程表面多次波预测与自适应相减方法研究[J]. 地球物理学报, 53(7): 1716-1724, doi: 10.3969/j.issn.0001-5733.2010.07.023. |
| [87] | 石颖, 王维红. 2012. 基于波动方程预测和双曲Radon变换联合压制表面多次波[J]. 地球物理学报, 55(9): 3115-3125, doi: 10.6038/j.issn.0001-5733.2012.09.029. |
| [88] | 石颖, 王维红, 李莹,等. 2013. 基于波动方程三维表面多次波预测方法研究[J]. 地球物理学报, 56(6): 2023-2032, doi: 10.6038/cjg20130623. |
| [89] | 王维红, 崔宝文, 刘洪. 2007. 表面多次波衰减的研究现状与进展[J]. 地球物理学进展, 22(1): 156-164, doi: 10.3969/j.issn.1004-2903.2007.01.022. |
| [90] | 谢宋雷, 刘伊克, 王一博,等. 2013. 深水陡坡带绕射多次波压制方法研究[J]. 地球物理学报, 56(9): 3118-3123, doi: 10.6038/cjg20130924. |
| [91] | 熊登, 赵伟, 张剑锋. 2009. 混合域高分辨率抛物Radon变换及在衰减多次波中的应用[J]. 地球物理学报, 52(4): 1068-1077. |
| [92] | 薛亚茹, 陈小宏, 马继涛. 2012. 多方向正交多项式变换压制多次波[J]. 地球物理学报, 55(10): 2450-3458, doi: 10.6038/j.issn.0001-5733.2012.10.028. |
| [93] | 赵昌垒, 叶月明, 姚根顺,等. 2013. 线性拉东域预测反褶积在海洋多次波去除中的应用[J]. 地球物理学进展, 28(2): 1026-1032, doi: 10.6038/pg20130256. |
 2015, Vol. 30
2015, Vol. 30


